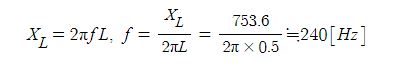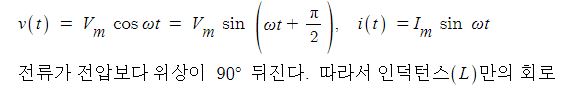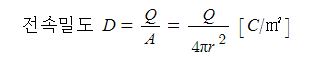아낌없이 주는 나무

제1과목 전기이론

1. 0.02 μF의 콘덴서에 12 μC의 전하를 공급하면 몇 V의 전위차를 나타내는가 ?

   ① 600          ② 900             ③ 1,200                  ④ 2,400

[해설] 전하량 Q = CV​

2. 다음 중 1 [V]와 같은 값을 갖는 것은 ?

   ① 1 [J/C]           ② 1 [Wh/m]                   ③ 1 [Ω/m]                 ④ 1 [A·S]

[해설] 1 [V]란 1C의 전하가 이동하여 한 일이 1[J]일 때의 전위차이다.

            ∴ 1 [J/C], ※ 전위의 단위 : [V], [J/C]

​

3. 다음 중 콘덴서의 정전용량에 대한 설명으로 틀린 것은 ?

   ① 전압에 반비례한다.                      ② 이동 전하량에 비례한다.

   ③ 극판의 넓이에 비례한다.              ④ 극판의 간격에 비례한다.

[해설] 콘덴서의 정전용량​

4. 정전용량 C[F]의 콘덴서에 W[J]의 에너지를 축적하려면 이 콘덴서에 가해 줄 전압[V] 은 얼마인가 ?

5. 정전 흡인력에 대한 설명 중 옳은 것은 ?

   ① 정전 흡인력은 전압의 제곱에 비례한다.      ② 정전 흡인력은 극판 간격에 비례한다.

   ③ 정전 흡인력은 면적의 제곱에 비례한다.      ④ 정전 흡인력은 쿨룽의 법칙으로 직접 계산한다.

​

[해설] 정전 흡인력 (평행판 전극의 단위 면적당)​

    ① 극판에 가한 전압의 제곱에 비례한다.

    ② 극판 간격의 제곱에 반비례한다.

    ③ 극판 면적에 비례한다.

​

6. 다음 설명 중 옳은 것은 ?

   ① 상자성체는 자화율이 0보다 크고, 반자성체에서는 자화율이 0보다 작다.

   ② 상자성체는 투자율이 1보다 작고, 반자성체에서는 투자율이 1보다 크다.

   ③ 반자성체는 자화율이 0보다 크고, 투자율이 1보다 크다.

   ④ 상자성체는 자화율이 0보다 작고, 투자율이 1보다 크다.

​

[해설] 자성체 (투자율 μs, 자화율 Χ )

   ⊙ 상자성체 : μs > 1인 물체로서, 자화율 X > 0

   ⊙ 강자성체 : μs ≫ 1인 물체로서, 자화율 X ≫ 0

   ⊙ 반자성체 : μs < 1인 물체로서, 자화율 X < 0

※ 자화 M, 자기장(자화세기) H, 자속밀도 B 일 때​

7. 공기 중에서 자기장의 세기가 100 [AT/m]인 점에 8 × 10-2 [Wb]의 자극을 놓을 때 이 자극에 작용하는 기자력은 [N]은 ?

   ① 8 × 10-2 [N]           ② 8 N               ③ 125 N                 ④ 1,250 N

​

[해설] 기자력 F = mH, F = 8 × 10-2 × 100 = 8 [N]

​

8. 전기와 자기의 요소를 대칭되게 나타내지 않는 것은 ?

   ① 전계 - 자계           ② 전속 - 자속             ③ 유전율 - 투자율               ④ 전속밀도 - 자기량

​

[해설] 전속밀도 D [C/㎡], 자속밀도 B [WB/㎡]

​

9. 자기회로의 길이 100 [㎝], 단면적 6.4 × 10-4 [㎡], 비투자율 50인 철심을 이용하여 자기저항을 구성하면 자기저항은

     몇 [AT/WB]인가 ? (단, μo = 4π × 10-7 [H/m])

   ① 7.9 × 107              ② 5.5 × 107            ③ 4.7 × 107                 ④ 2.5 × 107

​

[해설] 자기저항 (Reluctance)​

10. 평행한 두 도체에 같은 방향의 전류가 흘렀을 때 두 도체 사이에 작용하는 힘은 어떻게 되는가 ?

   ① 반발력이 작용한다.       ② 힘은 0이다.          ③ 흡입력이 작용한다.      ④ 1/(2πr)의 힘이 작용한다.

​

[해설] 평행도체 사이에 작용하는 전자력

   ㉠ 같은 방향일 때 : 흡인력                   ㉡ 반대방향일 때 : 반발력

​

11. 1AH는 몇 C인가 ?

   ① 7,200               ② 3,600                   ③ 120                      ④ 60

​

[해설] Q = I · t [A·sec] = 1 × 60 × 60 = 3,600 [C]

​

12. 2 Ω 과 3 Ω 의 저항을 병렬로 접속했을 때 흐르는 전류는 직렬로 접속했을 때의 약 몇 배인가 ?

   ① 1/2배              ② 2배                ③ 2.08배                        ④ 4.17배

​

[해설] 저항의 직·병렬 연결시 합성저항

   ㉠ 병렬접속시 합성저항​

   ㉡ 직렬 접속시 합성저항

        Rs = R1 + R2 = 2 + 3 = 5 [Ω]

      ∴ 전류의 비는 저항의 비에 반비례하므로 병렬 접속하였을 때 흐르는 전류가 4.17배가 된다.

​

13. 다음 그림에서 B점의 전위가 100V이고 C점의 전위가 60 V이다. 이 때 AB 사이의 저항 3Ω에 흐르는 전류는 몇 A인가 ?

    ① 2.14            ② 2.86               ③ 4.27                    ④ 5

​

[해설] ㉠ 점 B, C 사이의 전압 : VBC = VB - VC = 100 - 60 = 40 [V]

   ㉡ 전류 산정

14. 어떤 정현파 전압의 평균값이 200 [V]이면 실효값은 약 몇 [V]인가 ?

      ① 180               ② 222              ③ 282                   ④ 380

​

[해설] 실횻값 V = 1.11 × Va = 1.11 × 200 ≒ 222 [V]​​

15. 다음중 RLC 직렬회로에서 임피던스 Z의 크기를 나타내는 식은 ?​

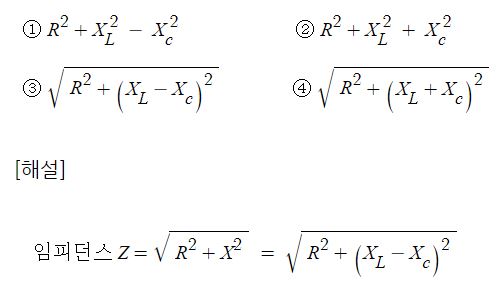
16. 다음 그림과 같이 전원과 부하가 다같이 △결선된 3상 평형회로가 있다. 상전압이 200 V, 부하 임피던스가 Z = 6 + j8

       [Ω]인 경우 선전류는 몇 [A] 인가 ?

   ① 20               ② 20/√3              ③ 20 √3                 ④ 10 √3

​

[해설]​

17. 다음 중 파형률을 나타낸 것은 ?

   ① 실효값 / 최대값         ② 최대값 / 실효값           ③ 실효값 / 평균값           ④ 평균값 / 실효값

​

[해설] ㉠ 파형률 = 실횻값 / 평균값,        ㉡ 파고율 = 최대값 / 실효값

​

18. 패러데이 법칙에서 화학당량은 무엇을 나타내는가 ?

   ① 원자가 / 원자량       ② 원자량 / 원자가         ③ 석출량 / 원자가           ④ 원자량 / 석출량

​

[해설] 페러데이 법칙 (Faraday's law)

   ㉠ 전기분해시 전극에 석출되는 물질의 양은 전해액을 통한 전기량에 비례한다.

   ㉡ 전기량이 같을 때 석출되는 물질의 양은 그 물질의 화학당량에 비례한다.

        ※ 화학당량 = 원자량 / 원자가

​

19. 묽은 황산 (H2SO4) 용액에 구리 (Cu)와 아연 (Zn)판을 넣으면 전지가 된다. 이 때 양극(+)에 대한 설명으로 옳은 것은 ?

   ① 구리판이며 수소 기체가 발생한다.          ② 구리판이며 산소 기체가 발생한다.

   ③ 아연판이며 산소기체가 발생한다.           ④ 아연판이며 수소 기체가 발생한다.

​

[해설] 볼타 전지 (Voltaic cell)

  ㉠ 묽은 황산 용액에 구리 (Cu)와 아연 (Zn) 전극을 넣으면, 두 전극 사이에 기전력이 생겨 약 1 [V]의 전압이 나타난다.

  ㉡ 분극 작용 (Polarization effect) 전류를 얻게 되면 구리판(양극)의 표면이 수소 기체에 의해 둘러 싸이게 되는 현상으로,

        전지의 기전력을 저하시키는 요인이 된다.

​

20. 다음 중 납축전지의 양극 재료는 ?

   ① 2H2SO4          ② Pb            ③ PbSO4          ④ PbO2

​

[해설] 납축전지

   ㉠ 납축전지는 2차 전지의 대표적인 것이다.

   ㉡ 양극 : 이산화납 (PbO2)

   ㉢ 음극 : 납 (Pb)

   ㉣ 전해액 : 묽은 황산 (비중 1.23 ~ 1.26) 으로 사용한 것이다.

​

​

[정답] 1. ① 2. ① 3. ④ 4. ② 5. ① 6. ① 7. ② 8. ④ 9. ④ 10. ③  11. ② 12. ④ 13. ② 14. ② 15. ③ 16. ③ 17. ③ 18. ② 19. ①

           20. ④

​

#전기기능사 #모의고사 #콘덴서 #전위 #전하량 #정전용량 #투자율 #전속밀도

#자기회로 #파형률 #정현파 #페러데이 #납축전지 #볼타전지 #양극재료

수두(水頭)

높은 곳에 있는 물이 가지는 기계적 에너지, 압력, 속도 따위를 물의 높이로 나타낸 값. 물이 기준면에서 높이 h의 위치에 있을 경우 h를 위치 수두, 압력이 p일 경우 p/ρg(ρ는 밀도, g는 중력 가속도)를 압력 수두, 속도 v로 흐를 경우 v2/2g을 속도 수두, 이들의 합계를 전수두라 한다.

​

※ 일과 에너지

▣ 일반적으로 힘은 질량 × 가속도, 즉 F = ma로 표현한다.

  즉, 힘은 질량과 가속도에 비례한다. 힘은 질량과 가속도의 곱으로 나타낸다.

   ⊙ 그런데 지구상에서는 중력가속도가 작용하므로 F = mg 로 나타낸다.

▣ 일은 힘과 거리로 나타낸다. 즉 일은 힘 × 거리, 즉 일 [J, W] = F × H = mg × H로 나타낸다.

     또한 일률(동력)은 시간당 일 즉 단위시간당 일할 수 있는 능력이다.  

     즉, 일률(동력) = 일 /시간 = 일 / sec = 힘 · 거리 / sec = F·H /se = ρ · V · g · H /sec

     F = m·g = ρ · V · g ( ρ : 밀도, V : 부피) ⇒ ρ · g · V/s · H = ρ · g · Q · H 으로 나타낼 수도 있다.​

▣ 우리는 일률의 기준으로 물이 가지는 위치에너지 수두로 표현하는데 이를 정리하면 다음과 같다.

     수두 P = 밀도 × 중력가속도 × 시간당 부피 × 거리로 나타낼 수 있다.

     즉, P = ρ · g · V/s · H = [kg/㎥] × 9.81 [m/sec2] × [㎥/sec] × [m] 이다.

1. 전동기의 용량

 ▣ 전동기 용량을 구하는 식은 수두공식을 그대로 적용하면 된다.

  ⊙ 양수량이 ㎥ 또는 ㎥/s 에 따라 시간 t[sec]의 위치가 바뀌게 된다.​

  ※ 전동기 용량 : 투입일률      =           필요한 일률

                              P · t · η      =            9.81 Q · H · k

​

2. 전동기의 용량 (제연설비)

※ 공기의 밀도

공기의 밀도를 구할 수 있을까?

공기는 질소와 산소, 그리고 미량의 여러 기체가 섞인 혼합물이다. 고도와 지역에 따라 그 비율이 조금씩 다르겠지만,

대체로 질소(N2) 78 %, 산소(O2) 21 %, 그 밖의 기체 1 %(아르곤 0.9 % 외) 로 이루어졌다 말한다.

여기서의 비율은 부피 퍼센트(%, v/v)다.

​

아보가드로 법칙에 따르면, 일정 온도와 압력 조건에서 기체의 부피는 입자수와 비례한다.

우리는 공기의 부피 퍼센트를 알고 있다. 총 100 개의 공기 입자(?)가 있다면,

그 중 78 개는 질소, 21 개는 산소, 아르곤 1개라는 뜻이다.

​

또한 0 ℃, 1 기압 조건에서 모든 기체 1 몰의 부피는 22.4 L이다.

온도조건이 바뀌뀌어 25 ℃, 1 기압 조건에서 기체 1 몰의 부피는 약 24.5 L 2이다.

위의 부피 퍼센트에 따라 24.5 L 공기 1 몰 중 0.78 몰은 질소, 0.21 몰은 산소, 0.01 몰은 아르곤 기체다.

성분 기체의 몰질량 [g/mol]과 몰수 [mol]를 이용하여 해당 기체 혼합물의 질량을 구할 수 있다.

​

* 25 ℃, 24.5 L 에 포함된 공기(질소, 산소, 아르곤)의 질량 [g]

​

   1) 질소기체(N2)의 질량 [g] = 0.78 [mol] * 28 [g/mol] = 21.84 [g]

   2) 산소 기체(O2)의 질량 [g] = 0.21 [mol] * 32 [g/mol] = 6.72 [g]

   3) 아르곤 기체(Ar)의 질량 [g] = 0.01 [mol] * 40 [g/mol] = 0.4 [g]

​

∴ 공기의 질량 [g] = 21.84 + 6.72 + 0.4 = 28.96 [g]

​

    즉, 25 ℃, 24. 5 L의 부피 해당하는 공기의 질량은 28.96 [g]이다. 이를 밀도로 나타내면, 1.18 [g/L]다.

공기의 밀도 [g/L] = 28.96 / 24.5 = 1.18 [g/L] (25 ℃, 1기압 조건)

​

     국제협약을 통해 탄소 원자 1개의 질량을 12 amu (atomic mass unit) 라고 기준으로 정했습니다.

​

▣ 제연설비의 전동기 용량 산정에 있어서도 마찬가지로 수두를 사용한다.​​

여기서, P : 전동기 용량 [kW], PT : 전압(풍압) [㎜Aq, ㎜H2O], Q : 풍량 [㎥/min],  k : 여유율(전달계수), η : 전효율

※ 760 [㎜Hg] = 10,332 [㎜H2O]

     ℓpm : liter per minute : ℓ / min = 10-3 [㎥/min ]

     CMH : ㎥/hour

​

3. 전력용 콘덴서의 용량

▣ 전력용 콘덴서 용량은 역률(cosθ)를 이용하여 산정한다.​

         여기서, Qc : 콘덴서의 용량 [kVA], P : 유효전력 [kW],  cosθ1 : 개선 전 역률, cosθ2 : 개선 후 역률

4. 조명

  ① 조명 유도식​​

           여기서, F : 광속[lm], U : 조명률[%], N : 등 개수, A : 단면적 [㎡],  E : 조도 [lx], D : 감광보상률 [1/M] [%], M : 유지율

  ② 실지수 (Room index) : 조명률 계산의 기초로 실(방)의 크기와 모양에 따른 지수​

5. V결선시의 단상변압기 1대의 용량​

6. 전동기의 동기속도 및 회전속도

  ① 동기속도 (회전자계 속도)​

  ② 회전속도 (실제 회전속도)​

7. 감지기와의 배선회로에서의 감시전류, 작동전류

  ① 감시전류​

  ② 작동전류​

[감지기 배선도]

8. 비상용 자가발전기의 용량

  ① 부하중 가장 큰 유도전동기 기동시의 용량으로 구하는 방법​

  ② 비상용 자가발전기 차단기의 용량​

9. 누설전류

10. 분기회로수

11. 전선의 단면적 및 전압강하

   ※ 여기서 A : #전선 #단면적 [㎟] L : 전선길이 [m] I : 전부하 #전류 [A]

  ​ ▣ 전선의 공칭 단면적 [㎡]

  ▣ 전선관내에 전선 면적

    가. 금속관, 합성수지관

       ① 동일 굵기의 전선 : 48 [%] 이하

       ② 다른 굵기의 전선 : 32 [%] 이하

    나. 금속 덕트 : 20 [%] 이하

​

12. 전압강하

  ▣ 입력전압과 출력전압의 차이 : 송전에서 에너지의 손실

    여기서, e : 전압강하[V], Vs : 입력전압 [V], Vr : 출력전압(단자전압) [V],  I : 전류[A], R : 저항 [Ω]

​

13. 축전지의 용량

  ① 축전지의 용량 (시간에 따라 방전전류가 일정한 경우)​

  ② 축전지 용량 (시간에 따라 방전전류가 변하는 경우)

   여기서,  C : 축전지용량 [Ah], L : 용량저하율(보수율), K : 용량환산시간[h], I : 방전전류[A]

​

  ※ 용량저하율(보수율)

    ▣ 축전지설비에서 축전지를 장시간 사용하거나 사용조건 등의 변경으로 인한 용량변화를 보상하는 보정치로

         보통 0.8을 적용한다.

  ③ 축전지의 공칭전압​

   ④ 축전지 1개의 허용최저전압

       여기서, V : 축전지 1개의 허용최저전압 [V/cell]

                   Va : 부하의 허용최저전압 [V]

                   Vc : 축전지와 부하간 접속선의 전압강하 [V]

                     n : 직렬접속 단전지 개수

​

14. 2차 충전전류 및 2차 출력

  ① 2차 충전전류​

  ② 2차 출력

     ▣ 2차 출력 = 표준전압 × 2차 충전전류 [kVA]

​

15. 합성정전용량 (콘덴서 직렬접속시)

  ① 직렬 접속시​

           여기서, C : 합성정전용량[F], C1, C2, C3 : 정전용량 [F]

  ② 병렬접속시

          합성정전용량 C = C1 + C2 + C3 + ··· [F]

          여기서, C : 합성정전용량[F], C1, C2, C3 : 정전용량 [F]

​

16. 전선의 전기저항​

       여기서, R : 전기저항[Ω], ρ : 고유저항 [Ω·㎟/m], ℓ : 길이 [m], A : 전선의단면적[㎟]

     ※ 전선의 고유저항

17. 전선의 저항온도계수

   ① 온도에 의한 저항의 변화를 비율로 나타낸 것

   ② (+)일 경우 온도상승시 저항은 조금 증가한다.​

   여기서, R2 : t2 [℃] 에서의 도체의 저항 [Ω]

               R1 : t1 [℃] 에서의 도체의 저항 [Ω]

               at1 : t1 [℃]에서의 저항온도계수

                 t2 : 상승 후 온도 [℃]

                 t1 : 상승전 온도 [℃]

​

18. 전기계기의 오차​

     여기서, T : 참값, M : 측정값

​

#전동기 #용량 #제연설비 #풍량 #풍압 #효율 #양정 #콘덴서 #조명 #광속 #조명률

#조도 #변압기 #회전속도 #동기속도 #감지기 #감시전류 #발전기 #누설전류 #분기회로

#전압강하 #축전지 #보수율 #유지율 #정전용량 #고유저항 #저항온도계수

#오차율 #보정률

【전동기 기동법】

1. 유도전동기의 기동법

  ① 직입기동법 (전전압기동법) : 전원 전압으로 직접 기동하는 방법

    ▣ 전동기 단자에 전전압을 직접 인가하여 기동하는 방법으로 주로 소형 전동기에 사용되며 전동기기

        용량이 5.5 [kW] 미만에 사용된다.

  ② Y - △ 기동법

    ▣ 전동기에는 코일만 많이 감겨 있고 저항이 없으므로 코일에 의한 리액턴스가 발생하기전에는 초기 전류가 많이

         흐르므로 초기 기동전류를 작게 하기 위하여 전동기에 Y(Star)결선을 하여 기동하고, 정격운전(가속)이 된 후에는

         △(Delta)결선으로 변환하는 기동법으로 Y결선시 기동전류는 기동운전시의 1/3배로 작아지게 된다.

         주로 전동기용량이 5.5 ~37 [kW] 에서 사용되나 37[kW] 이상의 경우에도 사용하는 경우가 있다.

  ③ 기동보상기 기동법

    ▣ 기동용 3상 단권변압기 (기동보상기)로 전압을 감압하여 기동하는 방법으로 Y결선으로 기동을 하고 회전수가

         상승함에 따라 △ 결선으로 변경하는 기동방식이다.

         주료 전동기 용량이 22[kW] 이상에서 사용된다.

  ④ 리액터 기동법

    ▣ 기동보상기의 일종인 리액터를 이용하여 기동을 하며 리액터가 고가이며 조작이 복잡하며 리액터를 접속하여

          기동전류를 억제하여 기동하는 방법이다.

  ⑤ 반반 기동법 (단상전동기)

    ▣ 단상 유도전동기의 기동법으로 고정자가 여자되면 단락된 회전자 권선에 전압이 유기되고, 이 전압에 의해 전류가

         흐르고 자계가 형성되어 고정자권선이 만드는 자계와 상호작용으로 반발력이 발생한다. 기동토크는 전부하 토크의

         400~500% 정도이다.

​

【역률개선용 진상 콘덴서】

​

1. 방전코일을 설치하지 않는 경우

  ▣ 하나의 차단기로 부하와 진상콘덴서를 동시에 개폐하는 경우로서 부하에 있는 코일을 통하여 잔류전하를 방전시키므

      로 방전코일을 설치하지 않아도 된다.

  ※ 전동기에는 유도성 리액턴스가 많이 발생하므로 이 유도성 리액턴스를 상쇄하여 전동기의 역률을 개선하고자 콘덴서

      를 설치하게 되는데 전동기에 직접 콘덴서를 설치하는 경우이다.

2. 방전코일을 설치하지 않는 경우

  ▣ 하나의 차단기로 부하와 진상콘덴서를 동시에 개폐하지 않는 경우로서 방전코일을 설치하여 잔류전하를 방전시켜야

       한다.

   ※ 콘덴서를 전동기에 직접 연결하지 않고 회로에 연결하는 경우에는 콘덴서에 잔류 전하가 남게 되어 이를 제거하기

       위하여 방전코일을 선로간에 연결하여야 한다.

       즉 콘덴서에 축적되는 진상전류를 유도성 리액턴스로 다시 상쇄하게 된다.

【 출제 예상 문제 】

1. 역률개선용 콘덴서에 추가로 방전코일을 설치하여야 하나 실제 방전코일을 설치하지 않는 이유를 쓰시오.

   ▣ 부하에 있는 코일에서 발생하는 유도성 리액턴스가 잔류전하를 방전시키므로

​

2. 3상 380 [V] 30[kW] 스프링클러 펌프용 유도전동기이다. 기동방식은 일반적으로 어떤 방식이 이용되며 전동기의 역률이

     60[%]일 때 역률을 90[%]로 개선할 수 있는 전력용 콘덴서의 용량은 몇 [kVA]이겠는가 ?

  ① 기동방식 : Y-△ 기동방식 (이론상 기동보상기법)

  ② 전력용 콘덴서의 용량​

3. 콘덴서 회로의 주변기기에 대한 설명이다. 다음 각 물음에 답하시오.

  가. 투입시 과전압으로 부터 보호하고 개방시 콘덴서의 잔류전하를 방전시키며 콘덴서를 회로에서 분리시켰을 경우

        잔류전하를 방전시켜 위험을 방지하기 위한 목적으로 사용되는 것을 무엇이라고 하는가 ? 방전코일

  나. 제5 고조파에 따른 파형을 개선하는 기기를 무엇이라고 하는가 ? 직렬 리액터

​

4. 콘덴서 회로에 방전코일을 넣는 이유는 ? 콘덴서에 축적된 잔류전하를 방전시키기 위해

【 정류회로 및 전기 회로 】

​

1. 브리지형 정류회로

가. 콘덴서가 있는 회로

  ▣ 정류회로에 콘덴서를 설치하면 전하를 축적하게 되며 정류시에 파형을 완만하게 해 주는데 이를 콘덴서에 의한

       평활작용이라고 한다.

나. 콘덴서가 없는 회로

  ▣ 콘덴서가 없는 회로에서는 콘덴서에 의한 평활작용이 없게 되어 교류전압의 파형이 거의 그대로 나타나게 된다.

[참고] 단상반파정류회로

  ▣ 반파정류회로의 경우에는 파형이 끊어지는 단점이 있다.

【 세그먼트 구성 】

​

1. 세그먼트 구성회로

가. 세그먼트 회로

  ▣ 전광판 등의 숫자를 나타내는 구성회로로서 발광다이오드를 통해 구성한다.

나. 세그먼트 구성도

  ▣ 숫자판에서 각 구간에 발광다이오드를 설치하여 숫자를 나타낼 수 있다.

【 트랜지스터 (Transistor) 】

  ▣ 규소나 게르마늄으로 만들어진 반도체를 세 겹으로 접합하여 만든 전자회로의 구성요소로서 전류나 전압 흐름을 조절

        하여 증폭 및 스위치 역할을 한다.

【출제 예상 문제】

1. 다음은 브리지 정류회로 (전파정류회로)의 미완성 도면이다. 다음 각 물음에 답하시오.

  가. 정류 다이오드 4개를 사용하여 회로를 완성하시오.

  나. 회로내에서 C의 역할을 쓰시오 : 직류전압을 일정하게 하기 위하여

       ▣ 평활작용 : 정류의 파형을 완만하게 하기 위하여

​

2. 브리지형 전파정류회로와 출력전압의 파형을 그리시오 (단, 입력은 사용전원이다.)

3. 그림은 자동화재탐지설비의 R형 수신기 중에서 지구표시등회로의 일부분이다.

    다이오드 메트릭스 회로를 사용하여 경계구역을 표시하고자 할 때 다이오드를 추가하여 회로를 완성하도록 하라.

     (단, 그림의 1~8은 1~8 경계구역을 의미한다)

[답안작성]

4. 트랜지스터는 그 접합형태에 따라 npn 트랜지스터와 pnp 트랜지스터 2종류로 나눈다. 다음 트랜지스터의 구조를

     참조하여 기호(심벌)를 그리시오.

[답안작성]

#전동기 #기동법 #기동보상기 #리액터 #콘덴서 #방전코일 #직렬리액터 #역률

#정류회로 #세그먼트 #다이오드 #트랜지스터 #파형 #자동화재탐지설비

#경계구역 #메트릭스 #게르마늄 #규소

1. 보호계전기 : 기기와 선로의 보호기기

가. 사용 목적에 따른 종류

   ① 과전류 계전기 (OCR) : #과전류 발생시 동작하는 계전기

   ② 과전압 계전기 (OVR) : #과전압 발생시 동작하는 계전기

   ③ 부족전압 계전기 (UVR) : #부족전압 발생시 동작하는 계전기

   ④ 지락계전기 (GR) : 지락 사고 시 지락전류에 의해 동작하는 계전기 (접지계전기),  #영상변류기 ( #ZCT ) 필요

   ⑤ 열동계전기 (THR) : 전동기 등에 과부하 보호용으로 사용하는 계전기

​

나. 기기 (발전기, 변압기)의 내부 고장 검출

2. 콘덴서의 종류

가. 마일러 콘덴서

   ① 플라스틱 필름을 유전체로 한 콘덴서

   ② 용량의 정밀도가 높고 주파수 특성이 우수

나. 마이카 콘덴서

   ① 운모와 금속박막으로 되어 있거나, 운모 위에 은을 발라서 전극으로 만든 콘덴서

   ② 온도변화에 의한 용량변화가 작고 절연저항이 높은 우수한 특성

   ③ 표준콘덴서로 사용

다. 세라믹 콘덴서

   ① 비유전율이 큰 산화티탄 등을 유전체로 사용한 콘덴서

   ② 가격 대비 성능이 우수하여 가장 많이 사용

라. 전해 콘덴서

   ① 전기분해하여 금속의 표면에 산화피막을 만들어 이것을 유전체로 이용한 #콘덴서

   ② 주형으로 큰 정전용량을 얻을 수 있음

   ③ 극성을 가지고 있으므로 교류회로에는 사용 불가

​

3. 전선의 굵기

가. 전선의 굵기 결정 3요소

   ① 허용전류 (가장 중요한 요소)

   ② 전압강하

   ③ 기계적 강도

​

나. 전선 접속시 주의사항

   ① 접속부는 노출시키지 말 것

   ② 접속부분의 절연 성능은 타 부분과 동등 이상이 되도록 할 것

   ③ 접속점의 전기저항이 증가하지 않도록 할 것

   ④ 전선의 세기를 20[%] 이상 감소시키지 말 것

​

다. 전선 단면적의 계산

           여기서, A : 전선의 단면적[㎟], L : 선로길이 [m], I : 부하전류 [A]

                        e : 각선로간의 전압강하[V], e' : 각 선로간의 1선과 중성선 사이의 전압강하[V]

​

라. 저압 옥내배선의 준공 검사시 측정시험

   ① 절연저항 측정          ② 접지저항 측정            ③ 도통시험

​

4. 지시전기계기의 구성요소

   가. 구동장치 (Driving Device)

   나. 제어장치 (Controlling Device) : 스프링제어, 중력제어, 전자 제어

   다. 제동장치 (Damping Device) : 공기제동, 와전류 제동, 액체 제동

​

【 출제 예상 문제】

​

1. #변압기 내부회로 고장검출용으로 사용되는 계전기는 ? ①

   ① 비율차동계전기           ② 과전류 계전기            ③ 온도계전기              ④ 접지계전기

[해설] #비율차동계전기 : 발전기나 변압기의 내부고장 보호용 (내부회로 고장 검출용)

​

2. 열동계전기 (Thermal relay)의 설치 목적은 ? ①

   ① 전동기의 과부하 보호          ② 감전사고 예방          ③ 자기유지             ④ 인터록 유지

[해설] #열동계전기 (Thermal relay) : 전동기의 과부하 보호

​

3. 3상 3선식 전원으로 부터 80[㎝] 떨어진 장소에 50[A] 전류가 필요해서 14 [㎟] 전선

   으로 배선하였을 경우 전압강하는 몇 [V]인가 ? (단, 리액턴스 및 역률은 무시한다.) ③

    ① 10.17              ② 9.6                 ③ 8.8                    ④ 5.08

[해설] #전압강하 산정시​

  ▣ 저항(R)만의 회로에서는 전력은 P = V × I 로 구할 수 있다.

나. #리액터 (L)만의 회로

  ▣ L만의 회로에서는 전류가 전압보다 π/2(90˚)만큼 늦은 #지상전류 가 흐르게 된다.

    ⊙ 또한 전류와 전압의 위상차가 있어 극성이 서로 일정하지 않게 된다.

    ⊙ 전력 P의 파형도 #정현파(Sin파)를 이루므로 전체를 단순합산하면 0이 된다.

  ▣ 순시전력을 구해보자. 전력 P = 전압 V × 전류 I 이다.

  ▣ 평균 #전력 에 대하여 알아 보자.

    ※ L만의 회로에서는 에너지 소모가 없다. 평균전력이 "0"이다.

        L만의 회로에서는 충전과 방전을 계속하여 에너지 소모, 전력소모가 없다.

  ▣ 순시에너지에 대해 알아 보자

다. #콘덴서 C 만의 회로

  ▣ L만의 회로에서는 전류가 전압보다 π/2(90˚)만큼 앞선 진상전류가 흐르게 된다.

    ⊙ 또한 전류와 전압의 위상차가 있어 극성이 서로 일정하지 않게 된다.

    ⊙ 전력 P의 파형도 정현파(Sin파)를 이루므로 전체를 단순합산하면 0이 된다.

  ▣ #순시전력 을 알아 보자.

  ▣ #평균전력 에 대하여 알아 보자.

     ※ C만의 회로에서는 에너지 소모가 없다. 평균전력이 "0"이다.

         C만의 회로에서는 충전과 방전을 계속하여 에너지 소모, 전력소모가 없다.

  ▣ 순시 에너지에 대해 알아 보자.

4. 단상 교류 전력

  가. #피상전력 (공급전력) : 위상을 고려하지 않은 전압(V)와 전류(I)의 곱

  나. #유효전력 (평균전력, 소비전력) : 실제 일을 하는데 사용되는 전력을 말한다.​

  다. #무효전력 : 소비되지 않고 충전 되는 전력​

5. 역률과 무효율​

▣ 컬레( #공액 ) #복소수 의 예를 들어 보자.

      V = 100 ∠ 30˚ = 100 cos 30˚ + j sin 30˚

      공액복소수 V = 100 cos 30˚ - j 100 sin 30˚ = 100 cos 30˚ + j 100 sin (-30˚)

                             = 100 ∠ -30˚

7. #역률 개선을 위한 콘덴서 용량

  ▣ 전압과 전류가 일정하다면 소비전력의 크기는 저항에 의해 변하게 된다.

       그런데 #소비전력 은 저항의 제곱에 반비례하기도 하고 저항에 비례하기도 한다.

       이런 이유로 소비전력은 저항에 따라서 #포물선 을 그리게 된다.

       아래 그림을 통해서 이에 대해 알아 보자.

  ▣ 저항과 전력과의 관계를 볼 때, 전력곡선의 접선이 "0"이 즉 미분한 값이 영일 때

       전력은 최대가 된다. 이를 통해서 전력의 최대값을 구해 보자.

다. 최대전력 전송

   ① 12 [W]            ② 36 [W]                ③ 72 [W]                  ④ 144 [W]

[해설] 최대 전력 공급 조건 

Inductor와 Capacitor는 전기를 하면서 늘 옆구리에 가랭이에 끼고 살아야 하는데도 불구하고

어째 두리뭉실하게 이해하고 넘어가게 되는 넘들중 하나인 것 같습니다.

그래서인지 초심자일수록 "대체 L은 뭐고, C는 뭐냔 말이닷!"이란 푸념을 늘어놓게 되지요.

아직도 L과 C가 대체 뭐하려고 있는 놈인지 아리까리한 분이시라면, 주의깊게 보시길 바랍니다.

​

L과 C를 이해하기 위해서는...

우선 대상용어의 정의를 이해하면 일단 반은 먹고 들어가는 겁니다. 하지만 L과 C라는 개념은, 단순히 정의로 파악하고

이해할 수 있는 대상이 아닙니다. 실제 활용상의 특성과 현상으로 습득해야 하는 문제입니다.

바로 이점이 초심자들을 힘들게 하는, 어쩔 수 없는 문제인 듯 합니다. 한마디로 그냥 말만 들어서 다 이해가 갈 만한

문제는 아니고, 실제로 회로나 시스템에 적용해가면서 습득해야 하는 부분이 많습니다.

그래도 L, C 동작특성과 활용에 대한 개념을 미리 정리해보는 것은 분명히 의미있는 일일 것입니다.

그럼 이제부터 L과 C의 특성에 대해 차근차근 알아보도록 하지요.

​

먼저, Inductance와 Capacitance는 서로 반대되는 현상을 말합니다.

그러므로 L과 C는 정 반대의 특성과 현상을 보인다는 점을 미리 명심할 필요가 있습니다.

우선 관련 용어들의 고전적인 정의부터 정리해보겠습니다.

L과 C의 주파수 특성

​

위에서는 사전적으로 정의된 내용으로는 솔직히 주파수 특성을 정확히 판단할 수 없습니다.

그럼 이제 완전히 RF적인 관점에서 L과 C의 S21 투과 특성을 살펴보도록 하겠습니다.

수동소자이므로 S21이 0dB에 가까울수록, 즉 위로 올라붙을수록 신호가 손실없이 통과된다는 뜻이란건

다 아시죠?

자! 결론 났습니다.. 고주파 RF의 관점에서 L과 C라는 지표의 특성을 간결하게 정의해보겠습니다.

​

L (Inductance) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 방해하는가?

C (Capacitance) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 원활하게 하는가?

​

물론 이게 다는 아닙니다만, 우리가 Inductance가 존재하느니 Capacitance가 존재하느니 하는 기준은

바로 위의 특성을 통해 판단한다는 점 - #고주파 가 될수록 신호를 잘 통과시키느냐, 막느냐 -을 명심하시기

바랍니다.

바로 이 특성에 기반하여 Inductor와 Capacitor는 상황에 따라 적절한 용도로 사용되고 있는 것입니다.

주파수를 가진 신호를 다룰 때 이 L과 C라는 요소를 적절히 사용하여 주파수 자원을 놨다가 풀었다가 함으로써

원하는 RF 회로와 시스템이 구현된다는 점!

이 개념을 명확히 익히고, 이제 L과 C의 자체적인 특성을 다시 들여다 보도록 하겠습니다.

​

L : #Inductance ( #인덕턴스 )

​

Inductance L은, 도선에 전류가 흐를 때 그 전류의 변화를 막으려는 성질, 또는 그 정도를 말합니다.

일종의 전기적 관성이라는 개념으로 볼 수도 있겠지요. 보수파라고 해야할까나..

즉 도선에 흐르는 전류가 직류(DC)라면 아무 변화없이 걍 흘러주지만,

그것이 변하려고 하면 막 화를 냅니다. 가만히 있는데 왜 건드리냐고...

결국 전류가 원래 흐르던 방향이나 크기가 바뀌려고 하면 그 반대의 기전력을 만들어서 그 변화를 막으려고 하지요.. 그래서 전류/전압파형의 크기, 방향이 주기적으로 변하는 교류(AC)가 입력되면 그 변화를 막으려고 안간힘을 쓰게 됩니다. 그래서 DC는 잘 통과하지만 AC는 좀체 통과하기 힘들 게 만드는 것이지요.

이게 무슨 원리라고 말하긴 좀 그렇고, 예전에 학자들이 이러한 교류변화의 흐름을 막고자 하는 그 성질을

뭐라고 부를까 ....하다가 그걸 Inductance 라고 부르기로 한 것입니다.

그럼 갑자기 질문!

​

Q : 그렇다면 이런 #inductance 는 어디에서 발생할까요?

A : 길이를 가지는 모든 선로에서 발생합니다.

​

그렇습니다. 아래 그림을 보시지요.

아무 선로건 그 선로 길이 방향으로 둥글게 자기장을 형성하게 되는데, 만약 이 선로를 따라 흐르던 전류가 변화하려

하면 그 주변에 생성된 자기장도 같이 바뀌야만 합니다.

(오른손 법칙 다 기억하시죠? ^^)

바로 이렇게 선로주위에 생성된 자기장이 선로의 전류/전압 변화를 따라 가려면

어느정도 시간이 필요해집니다.

결국 자기장이 한박자 늦게 변하려 하다 보면 (또 사실은 별로 변하고 싶어하지도 않을 겁니다. 직접 물어본건 아니지만...) 결국 도선의 전류변화를 방해하는 꼴이 되는 것이지요.

그리고 이러한 주변의 자기장이 많이 생길수록 (즉 L값이 커질수록) 전류가 변화하기가 무척 힘들겁니다.

주변의 자기장을 일일이 설득해서 자기를 따라 변하게 해야 하는데,

그 대상이 많아질수록 쉽지가 않은 것입니다.

그래서 L값이 높을수록 고주파는 통과하기 힘들어 하는 것이지요.

그럼 또다시 자문자답을 해보겠습니다.

​

Q : 그렇다면 inductance를 유발시키는 inductor는 어떻게 만드나요?

A : 선로를 기 ~이~일~게 만들면 됩니다.

​

아주 간단하지 않습니까?

선로만 길면 주변의 자기장은 길이만큼 점점더 늘어나니까 Inductance는 죽죽 늘어나줍니다.

그런데 무식하게 마냥 길게만 만들 수는 없으니, 둘둘 감아서 스프링모양의 coil로 만들게 되죠.

그래서 coil = Inductor처럼 공식화된 것이구요.

여기서 한가지 짚고 넘어갈 것은, 이렇게 coil형태로 만들어 놓으면 실제 그 선로 길이만으로 구현한 것보다

L값을 증가시킬 수도 있습니다. 왜냐하면, inductance는 self inductance(자기유도)와 mutual inductance(상호유도)가 존재하기 때문입니다. (이 정도는 고딩때도 배우죠...)

mutual inductance는 위의 그림과 같이 방향에 따라 다른데, 만약 전류가 같은 방향이라면

상호간의 주변의 자기장이 서로 더해져서 L값은 더더욱 세집니다.

반면 반대로 전류가 서로 다르게 흐르고 있다면 서로간의 자기장 방향이 달라서 상쇄가 되기 때문에

전체적인 L값이 작아지는 효과가 발생합니다.

RF에서 Inductance를 유발하는 Inductor는 일반 저주파에서처럼 coil형태로 감긴 긴 선로를 lumped

element로 사용하기도 합니다. 만약 Microstrip과 같이 패턴을 통해 구현하려면 역시 선로를 길게만

만들어도 가능합니다. 다만 공간적 제약이 있으므로 패턴을 이용하여 Inductance를 구현하려면

아래와 같은 세가지의 Inductor형태를 주로 이용하게 됩니다.

보시면 아시겠지만 좁은데다 선로를 길게 깔 수는 없으니 그냥 생각나는대로 꼬아놓는 방식입니다. 이중 Spiral Inductor가 그나마 많이 애용되는데, 한방향으로 동심원을 그리기 때문에 mutual inductance에서 같은 방향으로 자기장이 더해져서 작은 크기로 큰 L값을 만들 수 있는 장점이 있습니다. 다만 대체로 loss가 심해서 사용에 주의를 기울여야 합니다. 그리고 중앙부에서 다른쪽으로 연결해야 하기 때문에 반드시 air bridge나 다층 선로를 이용해야 한다는, 공정상의 치명적인 약점이 있습니다.

그옆의 meander line은 air bridge가 필요없도록 그냥 뱀처럼 꼬아놓은 것입니다. 그런데 이놈은 mutual inductance가 반대로 일어나기 때문에 서로 상쇄되어 크기에 비해 그다지 높은 L값을 만들기가 힘들다는 치명타가 있습니다. 그리고 마지막 loop inductor는, 모양도 구리고 성능도 구려서 많이 사용하진 않습니다. 다만 filtering 특성이 있어서 가끔씩 사용하긴 합니다.

자, 이것이 inductance와 inductor의 기초개념입니다. 잘 생각해보면 별로 어렵지도 않은 개념이지요?

C : Capacitance ( #커패시턴스 )

​

L을 이해했으니 이제 C를 이해해보지요. C는 L의 정반대 성질을 갖고 있습니다.

Capacitance C는 단절된 금속사이에서 전류/전압의 변화가 있을 때만 신호를 통과시키려는 성질,

또는 그 정도를 말합니다.

Capacitor의 아이콘을 잘 보면 선로가 끊어져 있는 것처럼 보이죠? 실제로도 끊어져 있습니다.

그렇다면 어떻게 신호가 통할 수 있을까요? 그것은 끊어진 도체 사이의 유전체에 그 열쇠가 있습니다.

위의 그림은 capacitor에서 신호가 도통되는 상황을 보여주는 그림입니다.

끊어진 금속판 사이에 채워진 유전체는 전하를 직접 흘려주지는 않지만, 유전체 내부에서 전극이 배치되어

전기적 방향성을 띠게 됩니다.

결국 한쪽 방향으로 전하가 흘러가기만 하는 직류(DC)는 통과할 수가 없습니다. 끊어져 있으니까요.

반면, 주기적으로 전압전류가 변화하는 교류(AC)의 경우에는 한쪽에 전극이 형성되면 그림과 같이 유전체

내에서도 전극이 쏠리면서 분극되고, 그 결과 상대쪽 금속판에도 반대의 전극을 형성시켜 줄 수 있게 됩니다.

그리고 그것이 주기적으로 변하면 건너편 금속의 전극이나 전압도 주기적으로 변화시켜 주게 되어 결국 끊어

진 금속판 사이로 교류파형의 변화형상, 즉 신호가 전달되게 되는 것이죠.

​

Capacitor에 직류를 흐르게 하면, 직류를 인가한 그 순간에는 잠시 전기가 흐르는 듯 하다가 뚝 끊어집니다. Capacitor는 전압/전류에 변화가 있을 때만 동작하기 때문에 직류가 새로 인가되는 그 순간에만 변화를 감지하고 잠시나마 전기가 흐르는 것이죠. 다시말해 직류에 있어서는 처음 전압이 인가된 순간에만 유전체가 분극을 일으키고는 이내 사라지기 때문에 전기적 신호전달이 불가능하게 됩니다.

​

반면 쉴새없이 변화하는 교류는, 이러한 유전체의 분극현상이 사라지기 전에 극성이 바뀌어 버려서 결국 그 변화하는 신호파형이 건너편으로 잘 전달되게 되는 것입니다. 그리고 얼마나 빠른 변화의 양상을 잘 전달할 수 있느냐를 나타내는 지표가 capacitance가 되는 것이죠.

​

Capacitor의 내부구조는 실제로 금속판사이에 유전체를 삽입하게 됩니다. 그 면적과 금속판간의 거리에 의해 Capacitance 값이 결정되고, 단순히 금속판을 사용하지 않고 여러 가지 형태의 금속을 사용하여 품질이 좋은 capacitor를 만들어내려고 노력하게 됩니다.

스미스차트에서의 L과 C

​

자, 우선 스미스차트에서의 L과 C를 함 보시지요.

아래는 입출력단에 50옴 포트를 인가한 pass-through 상태에서의 S11을 나타낸 것이라 R=1

(즉 normalize 하기전의 50옴)상의 결과입니다.

스미스 차트 원의 위쪽은 임피던스 허수부가 + 일 때, 아래쪽은 임피던스 허수부가 - 일 때를 나타내지요.

잘 모르셨다면 스미스차트상에 나온 좌표를 읽어보시면 바로 알 수 있습니다.

여기서 잠시 복소 임피던스의 수식을 들여다보도록 하겠습니다.​

보시다시피 L값은 +j로, C값은 분모의 j가 분자로 올라가면서 -j값을 의미하는 것이죠. 다시말해 임피던스의 허수부가

+값이 나타나면 inductance 성분이 있다는 의미이고, -값이 나타나면 capacitance 성분이 있다는 의미가 됩니다.

그래서 스미스차트 좌표상에서 보면 L은 위쪽면에, C는 아래쪽면에 나타나게 되는 것입니다. 인덕터가 오른

쪽 R=1 인 원상에 올라가 있다는 것은 R값이 matching된, 즉 손실이 없는 상태를 의미하며,

이상적인 inductor와 capacitor는 위와 같은 그래프가 출력되어야 합니다.

​

#공진 (Resonacnce)

​

간단한 #공진현상 을 통해 L과 C에 대한 이해를 더 하도록 해보지요.

공진이란 특정 주파수에 에너지가 집중되어, 해당 주파수만 골라내거나 걸러내는 주파수 선택 특성이 나타나는 것을

말합니다. 그리고 공진이란 에너지 관점에서 볼 때 L 성분과 C 성분이 동시에 공존하면서 평형상태를 이루고 있는 지점을

의미하지요.

L과 C의 #주파수 특성이 정 반대라는 것은 이제 잘 아실텐데, 그럼 이 두 개를 붙이면 어떻게 될까요?

서로 반대되는 주파수 패턴을 가진 L과 C성분이 직/병렬로 만나게 되면 아래와 같은 형태로 두 특성이 합성된 결과가 나옵니다. 그림만 봐도 쏙쏙 이해가 가지 않나요?

그리고 L과 C가 평형을 이루면서 특정 주파수에 대한 선택적 특성을 갖게되는 바로 그 지점..

그것을 우리는 공진(resonance)라 부르는 것입니다.

​

#필터 에서의 L과 C

​

필터는 기본적으로 L과 C 성분의 직병렬 조합을 통해 만들어집니다. L과 C 자체를 잘 생각해보면 각각 Lowpass 특성과 Highpass 특성을 갖고 있다는 것을 눈치챌 수 있지요. 그걸 좀더 다듬고 조합해서 원하는 주파수, 원하는 감쇄 특성을 가지는 어떤 구조를 만든 것, 그것이 바로 ' Filter ' 입니다.

자, 단순무식하게 아래의 LPF 그림만 한번 보겠습니다. 번호대로 보시길...

그림에 설명이 다 나와 있으니 별다른 부연설명은 필요 없겠지요? HPF의 경우는 L과 C의 소자 위치를 정반대로 바꾼 것입니다. 결국 모든 filter는 저런 Inductance와 Capacitance를 잘 조절해서 만드는 것입니다. 한가지 미리 명심할점은 꼭 inductor, capacitor소자같은 lumped element로만 만드는 것은 아니라, 어떤 구조든 Inductance와 capacitance를 유발할 수 있다면 그것들을 조합하여 다 filter로 만들 수 있다는 점입니다.

​

SRF (Self Resonating Frequency)

​

사실 지금까지 위에 언급한 L과 C에 대한 내용은 모두 ideal한 경우였습니다. 실제로 inductor와 capacitor를 사용할 때 꼭 알아두어야 할 것이, 바로 SRF(자기공진주파수)입니다. 아래는 실제 Inductor의 S21을 나타낸 그림입니다.

자, 이것은 무엇을 말하느냐면.. Inductor건 Capacitor건 특정 주파수를 넘어 버리면 자신의 역할이 반대로 뒤집어진다는 것입니다. Inductor가 Capacitor로 동작해 버리고, Capacitor가 Inductor로 동작해 버리는 황당한 상황이 발생한다는 것이지요. 그래서 이렇게 역할이 깨져버리는 주파수점이 마치 공진점과 같기 때문에 Self Resonating Frequency라 불리우는 것입니다.

그래서 모든 Inductior, Capacitor를 사용할 때는 반드시 SRF보다 어느정도 낮은 주파수에서 사용해야 하며, 특히 Inductor 쪽에서 더 주의를 요합니다. 아래는 실제 소자의 Inductor와 Capacitor의 S 파라미터그래프를 보여준 것입니다. 둘다 특정 주파수 이후로 본연의 기능을 잃고 반대의 소자로 동작하고 있습니다.

그렇다면 왜 실제상에서 이런 일이 발생하느냐? 아래의 Sprial Inductor의 예를 함 들여다보죠.

Spiral Inductor를 자세히 보니, 금속 길이와 상호인덕턴스의 증가로 인해 L값이 존재하지만, 각 금속간의 간격이 존재하기 때문에 그 간격에 의해 Capacitance가 존재합니다. 그리고 L과 C는 주파수가 올라갈수록 반대의 증가/감소 특성을 갖고 있기 때문에, 주파수가 올라가다 보면 두 역할이 바뀌어 버리는 것입니다.

​

다시 말해서 실제로 소자를 만들고 나면 Inductor에는 기생 capacitance가, Capacitor에는 기생 Inductance가 생기기 때문입니다. 위의 spiral 구조는 물론 모든 Inductor/Capacitor에 위와 같은 문제가 발생합니다. 그래서 어느 주파수가 넘어서면 기생성분들이 진짜 성분들에 맞짱을 뜨게 되고, 바로 그 지점이 SRF 가 됩니다. 소자값이 커질수록 실제 소자의 물리적 구조도 커지는 것이기 때문에, 덩달아 기생성분도 더 커져서 결국 SRF는점점 작아집니다. 쓸 수 있는 주파수 영역이 좁아진다는 의미이죠.

​

대부분의 일반적인 lumped 소자들은 SRF가 수GHz 대밖에 안되서, 그 이하의 주파수에서만 사용해야 합니다. 결국 아주 높은 주파수에서는 lumped element를 사용하지 못하게 되고, 그래서 microstrip같은 분산소자로서 L, C를 구현할 필요가 생기는 것이지요!

​

인덕터와 커패시터의 Q

Q값에 대해서 많이 들어보셧을텐데, 간단한 정의인데도 불구하고 그 의미를 헷갈려 하시는 분들이 많은 듯 합니다. Q는 여러 의미가 있지만, Inductor와 Capacitor에서의 Q값이란 아래와 같은 의미입니다.​​

즉, 임피던스의 허수부/실수부를 말합니다. 임피던스의 허수부는 L, C 값을 의미하며 실수부는 저항값을 의미하지요. 결국 이게 무엇을 의미하느냐? 소자의 loss가 얼마이냐 입니다. 리액턴스 X는 L과 C 같은 무손실성 저장성분을 말합니다. 그냥 전기장 혹은 자기장의 형태로 주파수별로 에너지를 축적하는 기능이죠. 반면 분모에 있는 R값은 저항값, 즉 저항에 의한 손실을 의미합니다.

​

물론 inductor건 capacitor건 저항에 의한 loss가 없어야 정상이겠지만, 사람 하는 일이 다 그렇듯 만들다보면 이런저런 이유로 작은 저항값들이 생겨서 열손실이 발생합니다. 그래서 L 또는 C값을 이런 기생저항값으로 나눈 값을 우리는 Q(Quality Factor)라고 합니다. 이러한 Q값은 주파수에 따라 다르며, 또한 소자값에 따라 당연히 다릅니다.

​

결국 Q값이 클수록 loss가 적다는 의미가 되지요. 간단하지 않슴까? 소자에 loss가 많으면 쓸데없이 에너지만 소모되어 성능도 잘 안나올테니 가능하면 Q값이 높은 소자를 쓰는게 좋은것이죠. (물론 더 비싸겠죠)

이것을 실제 Inductor의 스미스차트를 통해 이해를 돕도록 해보겠습니다.

그림에 나와있듯이 Q값이 떨어져서, 즉 R값이 증가하면 손실이 늘고 결국 R=1 로 normalize된 실수 임피던스 원과 거리가 멀어지게 됩니다. 또한 Inductor로 동작해야할 이놈이 어느 주파수를 넘어서면서는 임피던스가 아래쪽 capacitance 영역으로 내려가 버렸습니다. 이렇게 L영역과 C영역을 넘어가는 그 포인트의 주파수가 바로 저 위에 설명한 SRF가 되는 것이지요.

SRF가 Inductor와 Capacitor의 이용범위를 알 수 있는 성능지표라면, Q값은 그 소자의 품질을 평가하는 아주 중요한 지표입니다.

​

RF에서의 L과 C

간단한 amp의 사례를 통해 L,C가 어떻게 사용되고 있는지 그림으로 한번 보도록 하겠습니다.

​

1. Impedance Matching (L, C)

회로의 목적에 맞는 Tr의 적절한 입출력 임피던스를 찾은 후, 그것을 각각 50옴 포트와 임피던스 정합을 시키기 위해 L, C 소자가 애용됩니다. 상황에 따라서는 microstrip과 같은 분산소자로 대치 가능합니다.

​

2. DC Block (C)

Capacitor는 직류를 통과시키지 못하므로 DC를 막기 위한 목적으로 C가 사용됩니다. Tr을 구동시키기 위한 바이어스용으로 들어온 직류전원이 Tr에만 인가되고, 다른 곳으로 새어나가지 않도록 입출력단에는 반드시 Capacitor가 필요합니다. Capacitor의 C값은 해당 회로의 주파수에 해당하는 신호가 잘 통과할 수 있는 임피던스값으로 설정하게 됩니다.

​

3. RF Choke (L)

Tr을 구동하기 위한 DC 전원선으로 RF 교류신호가 유입되면 에너지 손실 및 저주파 발진이 발생하기 때문에, 직류 전원이 들어갈 때는 inductor로 교류신호를 막아 버립니다. L소자는 직류는 잘 통과하고 교류는 차단하기 때문에, 적당히 높은 L값을 가지는 inductor로 choke 역할을 시켜 줍니다..

​

4. Bypass (C)

RF choke가 교류신호를 막는다고는 하지만 완벽하지는 않습나다. 그래서 전원단에는 병렬로 bypass capacitor를 달아서 미세하게 새어나온 교류신호를 추가적으로 제거해주지요. 직류전원은 C소자로 흐를 수 없고, 교류입장에선 C소자는 도통된 상태이므로, 교류신호는 전원단을 들어가지 않고 Capacitor로 갔다가 접지되어 죽어 버리게 됩니다. RF choke로 막는다 해도 저주파신호는 새어나가는 경우가 많기 때문에, 주로 이 저주파 신호가 loop를 만드는 것을 막아서 발진을 방지하려는 목적으로 저주파 신호가 잘 통과할 수 있는 큰 C값을 설정합니다.

​

5. Degeneration (L,C)

Tr의 접지 쪽에 L, C, R 소자등을 달면 신호의 degeneration(퇴화)를 불러일으켜 gain등이 떨어지지만, 안정도와 선형성이 좋아지기 때문에 종종 애용됩니다

이렇듯 L과 C는 위에서 설명된 주파수 특성에 의거하여, 해당 용도에 맞는 위치에 적절히 사용되는 것입니다. 원리와 개념을 알면, 그 용도는 누구라도 유추하여 사용할 수 있는 것이죠.

​

그런데 마지막으로 한가지 더 염두에 두어야 할 것이 있습니다. 지금까지 우리는 Inductor와 Capacitor라는 특정한 소자에 대한 개념적인 내용을 다루었습니다. 그런데 고주파 RF에서 중요한 요소는 이러한 실제로 많이 사용하는 lumped element뿐만이 아니란 점이 문제입니다. 이제 Inductance와 capacitance를 생각할 때, 그것이 당장 땜질이 가능한 눈에 보이는 어떤 소자를 지칭하는 것만이 아니란 점을 염두에 두셔야 합니다.

​

위에서 L과 C의 정의를 계속 보아오셨겠지만, 엄밀히 말해서 Inductor와 Capacitor는 그 L,C 성분을 고의로 강하게 유도한 소자일 뿐입니다. 그렇다면 역으로 말해서, 고의적이지 않아도 발생하는 L,C 성분도 분명히 있다는 점입니다.

​

그래서 긴 선로에서는 Inducatance 성분이 감지되고, 본의아니게 근접한 두 금속선로사이에는 Capacitance 성분(이걸 커플링이라 부르죠)이 나타난 다는 점입니다. 그러한 L,C 성분은 주파수가 높을수록 민감하며, 그래서 RF 설계가 까다로와지고 microstrip같은 형식의 분산회로가 필요해진 것입니다. 이 선을 잘 이해하고 극복해야지만, 진정한 RF를 구현할 수 있게 되는 것입니다.

▣ 저항은 기호를 R, 단위는 [Ω]을 쓴다.

  ▣ 저항 소자만 있는 교류회로에 전압을 인가하면 다음의 식이 성립된다.​

  ▣ 인덕턴스 소자만 있는 교류회로에 전압(기전력)을 인가하면 다음의 식이 성립된다.

     ⊙ 회로에 인가하는 전압(기전력)은 v(t) = Vm sin ωt [V] 이다.​

  ▣ 커패시턴스 소자만 있는 교류회로에 전압(기전력)을 인가하면 다음의 식이 성립된다.

    ⊙ 회로에 인가하는 전압(기전력)은 v(t) = Vm sin ωt [V] 이다.​

4. 0.5[H]인 #코일 의 #리액턴스 가 753.6[Ω] 일 때 주파수는 약 몇 [Hz]인가 ? ③

   ① 60 [Hz]             ② 120 [Hz]              ③ 240[Hz]                ④ 360 [Hz]

[해설] 유도성 리액턴스 XL = 2πfL ​

5. 60[Hz]에서 3[Ω]의 용량성 리액턴스를 갖는 콘덴서의 정전용량은 약 몇 [μF]인가 ? ③

   ① 564              ② 651                 ③ 884                       ④ 996

[해설] 용량성 리액턴스 (Xc) Xc =1/ωC = 1/2πfC​

          "두 점전하 사이에 작용하는 정전기력의 크기는 두 전하의 곱에 비례하고.

            전하 사이의 거리의 제곱에 반비례한다. 

① 진공중에서의 정전기력​

           여기서, E : 전계의 세기 [V/m], Q : 전하[C], r : 거리[m], V : 전압[V], d : 두께 [m],

           ε : 유전율 [F/m] (ε=εo· εs), εo : 진공의 유전율[F/m], εs : 비유전율

​

  ② #전기력

         F = QN [N]

         여기서, F : 전기력[N], Q : 전하[C], E : 전계의 세기 [V/m]

  ③ #전위

       여기서, D : 전속밀도[C/㎡], A : 단면적[㎡], Q : 전속[C], r : 거리 [m]

​

      위 식에서 분자, 분모에 ε을 곱하면​

      여기서, W : 정전에너지[J], Q : 전하[C], V : 전위[V], C : 정전용량[F]

​

나. 에너지 밀도

  ▣ 단위 체적당 축적 에너지(에너지 밀도) Wo는

    여기서, Wo : 에너지 밀도[J/㎥], E : 전계의 세기 [V/m], D : 전속밀도[C/㎡], ε : 유전율

                 [F/m], εo : 진공의 유전율 [F/m] , εs : 비유전율

​

[참고사항]

▣ 에너지를 구하는 식은 W = QV 이다. 여기서 W : 에너지, Q : 전하, V : 전압이다.

▣ 위의 에너지는 일반적인 에너지로 회로 전체 에너지를 말하며 전계 내에서 전하를 이동

    시킬 때 필요한 에너지를 말한다. 하지만 우리가 구하고자 하는 콘덴서에 축적되는 에너

    지이다. 콘덴서에 축적되는 에너지는 어떻게 구할까 ? 콘덴서에 축적되는 에너지는 일

    반 에너지처럼 W = QV로 구할 수 없다. 왜냐하면 콘덴서 내에서는 전압이 일정하지 않

    으므로 변하는 값이기 때문이다. 이러한 변화는 값의 합을 구하기 위해서는 적분을 이용

    하여 구하여야 한다.

[두 도체판의 에너지]

  이제 콘덴서에 축적된 에너지를 구하는 방법을 알았다.

  그렇다면 평평한 2개의 도체로 이루어진 콘덴서에서 전체 에너지를 조금더 자세하게

  풀어서 계산해 보자.

위 그림과 같은 도체 사이에 축적되는 에너지를 구해 보자.

우리가 2개의 평형판이 존재할 때 정전용량을 구하는 공식을 배웠다.

이 공식을 이용해서 에너지를 표현하였다.

위 그림을 보면 커패시터의 면적을 S라고 하고 두개의 도체의 간격을 d라고 하였을 때

S와 d의 곱은 두 개의 도체 사이의 부피를 나타내는 것이다.

따라서 Sd를 부피인 U로 표현하였다.

그렇다면 앞 공식을 이용하여 단위 체적당 에너지를 구할 수 있게 된다.​

2. 2개의 전하 사이에 작용하는 정전기력과 거리 사이의 관계는 ? ③

  ① 거리에 반비례한다.                       ② 거리에 비례한다.

  ③ 거리의 제곱에 반비례한다.           ④ 거리의 제곱에 비례한다.

[해설]​

3. #정전용량 C의 #콘덴서 에 W의 에너지를 축적하려면 인가전압은 몇 [V]인가 ? ④​

7. 3[μF]의 콘덴서를 4[kV]로 충전하면 저장되는 에너지는 몇 [J]인가 ?

      ① 1[J]                  ② 8 [J]                 ③ 16[J]                        ④ 24[J]

[해설] 정전에너지​