공진 (Resonance)의 정의
어느날 여러분이 길을 가다가 굉장히 맘에 드는 이성을 만났습니다.
곁눈질로 보다가 서로 지나쳐 걸어가다가.. 다시 한번 보고 싶어서 고개를 돌렸더니..
마침 그 여성도 뭔가 feel이 통해서 동시에 돌아보는 바람에 두 사람은 눈빛을 마주쳤습니다!
헐~ 웬 3류 드라마?
실제로 살다보면 그럴 수도 있겠지요. 뭔가 통하는 느낌이란게 있으니까요.
여러분들도 실제로 살면서 누군가와 강하게 교감을 느낀 적이 있으실 것입니다.
소위 공명(共鳴 : 같이 울림)한다고 하지요.
원래 공명은 소리 진동에서 사용하는 개념이지만, 소리 역시 어떤 주파수를 가진 성분입니다.
같은 주파수의 소리가 만나면, 서로 공명하면서 더 커지기 마련이죠.
그리고 또한 전자기파는 주파수라는 성분을 내제하고 있습니다.
광범위하게 공진의 의미를 정의하면 주파수 선택적 특성을 가지는 현상을 의미합니다.
모든 RF 시스템은 각자 사용하는 주파수대역이 정해져있습니다.
그렇다면 모든 RF시스템은 자기가 사용하는 특정 주파수 성분만 교묘하게 골라내어 처리해야 하는데,
이렇게 주파수를 선택해야 하는 모든 경우에 공진의 개념이 적용될 수 있습니다.
주파수 선택이라는 관점에서, RF에서의 공진은 매우 중요한 기능을 하는 현상입니다.
공진의 발생을 광범위하게 정의한다면 아래와 같이 두줄로 정의가 될 수 있습니다.
⊙ 밀고 당기는 힘이 평형을 이룰때
⊙ 서로 다른 에너지/특성의 주파수가 일치할 때
공진의 주파수 선택특성은, 입력되는 신호의 주기와 공진구조물이 가진 고유의 주기성이 일치됨으로써 발생
합니다. 이러한 공진의 발생은 크게 전기적 공진와 구조적 공진으로 나눌 수 있습니다.
우리가 이강의에서 주로 다루고자 핵심은 구조적 공진보다는 전기적인 공진현상의 이해입니다.
전기적 공진
전기적 공진은 소위 말하는 LC 공진을 말합니다.
인덕터와 캐패시터는 전/자기 에너지 축적소자입니다. 그러한 순간적인 전자기 에너지 축적과 방출 특성
때문에, 캐패시터와 인덕터는 정 반대의 주파수 특성을 보이지요.
인덕터는 주파수가 낮을수록 통과를 잘 시키는 특성이 있고,
캐패시터는 반대로 주파수가 높을수록 잘 통과시키게 됩니다.
그러한 두 특성의 소자가 한꺼번에 직/병렬로 붙으면 어떻게 될까요?
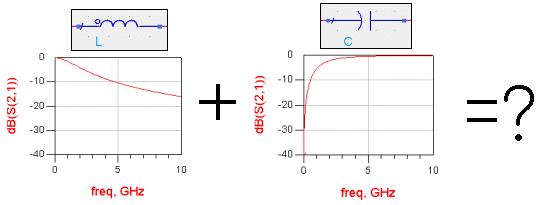
같은 주파수상에서 인덕터는 통과하지 못하도록 힘을 줄 것이며,
캐패시터는 통과할 수 있도록 용을 쓰게 될 것입니다.
그리고 둘중에 누가 더 강하냐에 따라 특정 주파수에서의 통과특성이 결정됩니다.
그렇게 평형을 이룬 상태의 결과는 바로 아래와 같은 형상이 되게 됩니다.
(아래 그림은 병렬공진의 사례입니다)
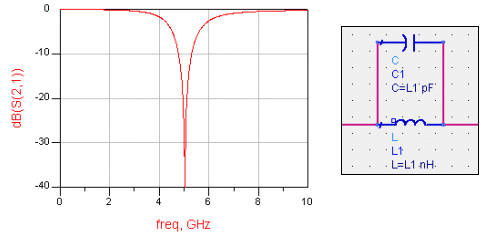
위의 예와 같은 병렬공진의 경우는 5GHz에서 S21이 -40dB로 매우 작아집니다.
즉 5GHz의 신호를 통과하지 못하게 막고 있는 band reject (notch) 특성이 나타나고 있는 것입니다.
이런 식으로 주파수를 선택적으로 막거나 통하게 할 때 우리는 공진(resonance)가 일어났다고 표현하게
되지요!
인덕터와 캐패시터의 특성만 잘 파악하면, 두 개의 특성 그래프가 섞였을 때 위와 같은 공진그래프가 나오는
것은 쉽게 이해할 수 있을 것입니다. 이것은 마치 동대문시장에서 에누리 협상하는 것과 같은 원리로 볼 수
있습니다. 밀고.. 당기고.. 그러다가 양쪽의 절충점을 찾아서 물건이 팔리게 됩니다. 서로 양보하다가 생각
(주파수)가 일치하는 지점에서 결정된 것이지요.
RF에서 인덕터와 캐패시터는 많은 유용한 특성을 갖고 있는데,
뭐니뭐니 해도 이처럼 L,C값의 조절에 의해 특정 주파수에 대해 선택적 특성을 만들 수 있다는 점,
즉 공진을 쉽게 유발해낼 수 있다는 점이 가장 중요하다고도 볼 수 있습니다.
LC 공진의 메카니즘
LC에 의한 전기적 공진의 원리가 무엇일까요? 조금은 어렵게 느껴질 수 있는 부분입니다. 이것을 이해하고
싶으시다면 아래의 설명을 차근차근 읽어보시면 결코 어렵지만은 않다는 것을 알 수 있습니다.
Step 1 ▶ L, C는 reactance 소자다!
자, 우선 인덕터와 캐패시터를 에너지 축적의 개념에서 다시 생각해 보도록 하지요.

#인덕터 -> 긴 선로 주변에 자기장의 형성하여 신호의 흐름을 주변에 자기장으로 저장한다.
캐패시터 -> 끊어진 금속 사이에 존재하는 #유전체 가 #분극하면서 전기장으로 신호의 흐름을 저장한다.
우리는 이러한 무손실 에너지 저장성 소자를 소위 reactance소자라고 부릅니다.
#임피던스 의 허수부로 표현되지요. 순간적으로 사라져 보이지만, 소모된 것이 아니라 잠시 어딘가에 저장되
어 있던 것입니다.
복소수 신호란 대체 무슨 뜻? 이란 강의에서 본 기억이 나지 않으십니까? #복소수 에서 허수는 존재하지 않는다는 의미가 아니라, 잠시 저장된 에너지 성분을 지칭한다는 점입니다.
그래서 L과 C의 임피던스는 허수로 표현되는 것이구요.
Step 2 ▶ reactance 소자는 진짜 무손실일까?
이러한 reactance 소자가 손실없이 에너지를 저장한다고 하지만, 정말 저장한 그대로 손실이 없는 걸까요?
왠지 그럴 것 같지는 않습니다.
복소수 강의에서 사용된 이론인 '여러분의 재산은 얼마?'를 상기해보신다면, 실수부는 현재 여러분 수중에 있는 돈이고, 허수부는 은행에 저금한돈, 전셋돈, 꿔준돈, 주식투자금 등으로 표현됩니다. 수중에 있는 돈은 진짜 여러분의 돈이지만, 나머지돈은 그냥 묵혀두거나 까먹고 있거나 사기를 당하거나 하여튼 뭔가 문제가 생기면 더 이상 꽁쳐놓은 돈이 아니라 그냥 손해가 발생해 버릴 수도 있습니다.
공교롭게도 세상의 현실과 전기회로가 일맥 상통하고 있습니다.
아무리 인덕터가 자기장으로, 캐패시터가 전기장으로 잠시 에너지를 축적할 수는 있다곤 해도,
그것을 어떻게 사용하느냐에 따라 그 저장된 에너지가 재활용될지 사장될지 결정됩니다.
다시말해서 L과 C로 인해 전/자기장으로 에너지가 축적된다해도 그걸 효율적으로 뽑아쓰질 않으면
그냥 사라져서 손실이 되 버릴 수도 있는 것입니다. 바로 이것이 공진을 이해하는 핵심입니다!
Step 3 ▶ 공진회로에서는 주파수별로 손실/무손실 여부가 다르다!
당췌 이런 리액턴스니 손실이니 하는 얘기가 왜 나오는지 하품이 나오기 시작할 지도 모르니
일단 그림부터 보세요.

분명히 인덕터와 캐패시터가 존재하는 회로를 거쳤는데도 불구하고, 출력단에서는 허수의 임피던스가 없는 것처럼 보이는 주파수가 존재합니다. 그래서 공진부를 통과하는 주파수의 임피던스 특성은 아래와 같은 그림을 그립니다. (대역통과 특성을 가진 직렬공진의 경우) 양의 허수 인덕터와 음의 허수 캐패시터가 서로 밀고 당기다가 허수 임피던스가 가장 낮아지는 바로 그지점, 공진점이 됩니다.
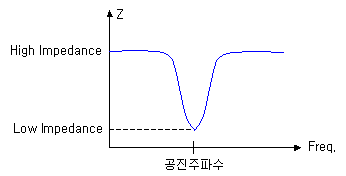
공진 주파수에서는 임피던스가 매우 낮아집니다. 즉, 출력임피던스가 낮은 주파수는 방해성분이 적어서
신호가 더 잘 흐를 수 있고, 나머지 주파수는 허수임피던스값이 사라지지 않고 커져서 손실로 작용하여
신호의 통과가 어려워집니다.즉 선택된 주파수 이외의 주파수 신호는 인덕터와 캐패시터에 의해 감쇄되어
버립니다. 뭔가 feel이 오지 않으십니까!
Step 4 ▶ 인덕터와 캐패시터간의 에너지 교환
LC 회로에 특정 주파수 신호가 인가되면 인덕터의 자기장으로 저장되었다가 캐패시터의 전기장으로 저장되었다가 하면서 줏대없이 왔다 갔다 하게 됩니다. 이 과정에서 인덕터와 캐패시터는 주파수별로 특성이 정반대이고, 한놈은 누르고 한놈은 올리고 하게 됩니다. 같은 주파수에서 인덕터는 그 흐름을 방해하고 싶어하고, 캐패시터는 흐름이 정지하는 것을 막고 싶어하면서 둘이 막 싸웁니다.
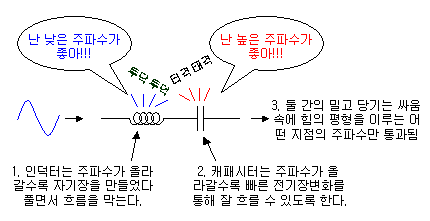
그래서 둘이 싸우다가 어느 한쪽이 이겨서 전기장이나 자기장 중 어느 한쪽으로 에너지 저장이 몰리게 되면, 손실이 발생해버립니다. 그냥 저장만 되 버리고 못써 버리게 되기 때문입니다. 그런데, 어떤 경우에는 둘이서 주거니 받거니 하는 에너지가 절묘하게 똑같아져서 캐패시터와 인덕터 어느 한쪽으로도 에너지 저장이 몰리지 않는 경우가 발생합니다. 누르고 올리는 힘이 평형을 이루는 되는 상황이지요. 이렇게 되는 주파수에서는 LC 소자가 손실없이 통과합니다. 그리고 나머지 주파수에서는 그 평형이 깨지기 때문에 손실이 쌓여서 신호의 통과가 어렵게 됩니다. 이 부분이 LC 공진의 두 번째 핵심입니다.
Step 5 ▶ #공진주파수
step 2에 나와있듯이 공진이 되려면 L,C가 존재하면서도 임피던스의 허수부가 0가 되어야 합니다.
#허수부 가 0이 되는 공진주파수를 찾는 수식의 증명은 매우 쉽습니다.
우선 복소 #임피던스 의 수식은 아래와 같습니다.
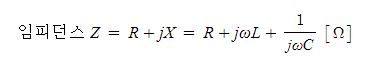
이중에서 허수임피던스가 0이 되어 없어지는 주파수가 공진주파수입니다.

이 식을 뒤집어서 f를 구하면 아래와 같이 공진주파수가 정해집니다.
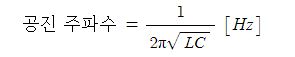
직/ #병렬 로 조합된 LC 회로에서 인덕터와 캐패시터가 #전기장 과 #자기장 으로 #에너지 를 축적하고 방출하면서 에너지를 주거니 받거니 하는 과정이 정확히 평형을 이룬 상태, 우리는 그것을 공진이라 부릅니다. 이것이 바로 LC공진의 정체입니다.
위의 수식에서 보시다시피 공진주파수는 L과 C가 곱해진 수치에 의해 결정됩니다. 즉 L과 C가 조합될 때마다 분명히 어떤 주파수에서 공진특성이 발생하게 됩니다. 한가지 관심있게 보아야 할 부분은, 같은 공진주파수라 하더라도 LC의 곱만 일정하면 된다는 점입니다. 즉 동일한 공진주파수상에서 L과 C의 조합은 많이 존재한다는 사실입니다.
LC 공진의 종류
크게 직렬 공진과 병렬 공진 두가지가 있습니다. 우선 1.5GHz에서 공진하는 두 LC소자의 직/병렬 소자 특성 곡선을 보시기 바랍니다.

백문이 불여일견! 같은 LC값의 경우에는 공진주파수는 동일합니다.
그런데 S파라미터는 정 반대로 동작하고 있는 것을 볼 수 있습니다.
LC 직렬공진은 Bandpass (대역통과) 형태의 공진이 발생하고,
LC 병렬공진은 Bandstop (대역저지) 형태의 공진이 발생합니다.
이렇듯 LC공진은 어떻게 연결하느냐에 따라 정반대의 특성이 나타날 수 있습니다.
위의 글들을 통해 공진의 개념을 접근하다보면, 자연스럽게 필터에 대한 생각이 떠오를 수 있습니다. 그렇습니다. 필터는 원하는 주파수대역만 통과시키려는 회로이고, 결국 철저하게 공진현상을 이용하게 됩니다. 경우에 따라 직렬과 병렬 LC 조합을 잘 이용하면 필터와 각종 주파수선택적 기능을 할 수 있는 공진부를 만들 수 있는 것이지요.
임피던스 매칭 = 공진 ?
공진은 곧 주파수선택적 특성을 말하므로 결국 필터의 동작원리 그 자체가 됩니다. 그리고 임피던스 매칭도 일종의 임피던스 변환성격의 필터입니다. 그렇다면... 임피던스 매칭은 공진일까요?
아시다시피 임피던스 매칭은 서로 다른 임피던스를 가진 두 단간에서, 특정 주파수에서 신호의 흐름을 좋게 만드는 것이 목적입니다. 즉 주파수 선택적 특성이 들어갑니다. 다시한번 강조합니다! 주파수 선택적 특성을 가지는 모든 경우는 공진의 개념에 포함됩니다. 결국 임피던스 매칭도 공진의 연장선상에 있습니다. 이것도 이참에 순서대로 이해해보도록 하지요.
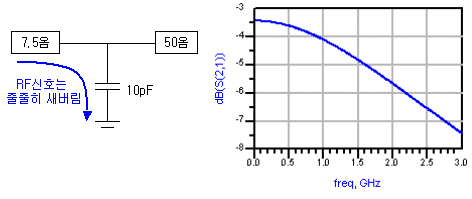
위의 그림은 7.5옴과 50옴의 서로 다른 임피던스간을 연결하고병렬로 10pF의 캐패시터를 달아놓은 예제입니다. 만약 이처럼 RF (AC)신호가 지나가는 선로에 병렬로 캐패시터가 붙어 있다면 어떻게 될까요? 캐패시터는 #고주파 가 될수록 임피던스가 낮아지면서 신호를 잘 통과시키는 소자이고, 그것이 병렬로 붙어있다면, short이 나겠지요? 결국 RF신호는 캡으로 신나게 도망가고 목적지로 가지 못할 것입니다.
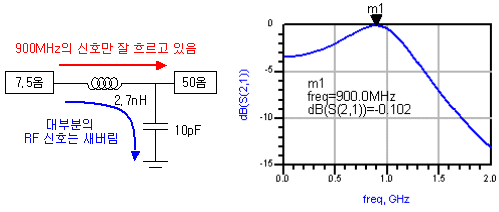
여기에 직렬로 2.7nH의 인덕터를 연결하면 LPF 형태의 매칭단이 구성됩니다. 그런데 여전히 RF 선로에 캐패시터가 병렬로 붙어 버려 있습니다. 허걱! 왠지 저 캐패시터로 RF신호가 줄줄히 샐 수도 있다고 생각되지 않습니까? 잘 생각해보니까 불안하죠? 분명히 병렬로 AC short가 잡혀 버렸는데..
그런데 S21 신호통과 그래프를 잘 보면 희한하게도 900MHz에서는 RF신호가 새지 않고 신호단을 잘 통과하고 있습니다. 이것의 비밀은 무엇일까요?
여기서 한가지 명확히 짚을 수 있는게 있습니다. 임피던스 매칭단에 병렬로 #캐패시터 가 있다고 해서 무조건 RF신호가 줄줄히 새지는 않는다는 점입니다. 정확히 말해서, 매칭되는 주파수의 신호가 새지 않는 것일 뿐입니다. 매칭주파수에서 멀어질수록 정말로 저 캐패시터로 신호가 줄~줄 새어나가서 결국 전달이 잘 되지 않게 됩니다. 엇! 이거 혹시 공진 아닐까요!
네, 이것도 공진입니다. 어째서 특정 주파수(=매칭주파수)에서만 병렬캐패시터로 에너지가 유출되지 않는가의 원인은, 매칭회로가 그 주파수에서 공진하고 있기 때문입니다. 병렬 캐패시터만 달려있으면 모든 주파수가 다 새나가겠지만, 직렬 인덕터가 같이 붙어 있으면서 병렬 캐패시터로 빠져나가는 에너지중 일부주파수를 끌어오게 됩니다. 그래서 특정 주파수 신호가 주기성을 갖고 변할때, 병렬 캐패시터와 직렬 인덕터가 그 주파수에 맞게 전기장과 자기장으로 에너지를 서로 손실없이 주고 받으면서 허수 임피던스를 0으로 만들어서 신호를 술술 전달시켜줍니다.

즉 병렬 캐패시터와 직렬 인덕터로 구성된 매칭단에서는 특정 주파수의 주기성과 일치하는 고유 공진주파수를 갖게 되고, 그것이 결국 매칭 주파수가 되는, 뭐 그렇고 그런 관계가 됩니다.
위 설명을 잘 곱씹어본다면, 인덕턴스와 캐패시턴스, 임피던스 매칭 그리고 공진의 개념이 일맥 상통하고 있다는 것을 깨달을 수 있으리라 생각됩니다. 굉장히 중요한 개념입니다. 아주 쉬운 개념이라고 말할 수는 없지만 여러번 곱씹어서 이해할 필요가 있습니다.
구조적 공진
전기적인 공진은 인덕턴스와 캐패시턴스의 조합에 의한 밀고당김으로 표현이 됩니다. 구조적 공진은 근본원리적으로는 유사하지만, 현상은 좀 다릅니다.
구조적 공진을 설명할 때 꼭 나오는 단어가 있는데 바로 cavity(공동 : 안이 비어있는 통,관)입니다. cavity는 내부가 공기 또는 유전체로 채워져있는 금속통을 의미합니다. cavity는 도파관처럼 사각형(rectangular)과 원통형(cylinder)이 있으며, 공정편의상 대부분 rectangular cavity가 많이 사용됩니다.

cavity내의 #전자기 파동은 zero-crossing point를 기준으로 반사특성이 발견됩니다. 그래서 아래와 같이 여러 mode로 공진을 하게 됩니다. 공진 mode는 cavity의 각 방향별로 얼마나 많은 반파장의 파동수가 존재하느냐로 표현됩니다.

대전력을 다루는 도파관 필터는 위와 같은 cavity를 연결하여 쉽게 BPF로 구성할 수 있습니다.
도파관 필터는 원래 생긴게 그래서 그렇다쳐도, 이런 cavity resonace는 housing에 의해서도 종종 발생한
다는 문제가 있습니다. 소위 케이스발진이라고도 불리우는 캐비티 발진은 모듈작업을 하면서 회로를 금속
케이스 내에 담다보면, 발생합니다. housing을 위한 금속벽들로 인해 그 자체가 cavity가 구성되기 때문입니다.
이것을 피하려면 케이스 자체를 설계할 때 사용주파수가 공진하지 않을 만한 구조적 크기인지 미리 계산할 필요가 있습니다. 또는 내부에 전자파 차폐용 페라이트 흡수체를 붙이는 것도 방법입니다. 특히 공진부를 만들어서 이용하는 발진기의 경우, 케이스 구조에 크게 영향을 받는 경향이 있습니다. 뚜껑을 닫으면 특성이 틀어지는게 오히려 당연한 현상입니다.
그래서 많은 시뮬레이션 툴을 잘 보면 마이크로스트립 조건을 정할 때 두께와 유전율말고, 케이스까지의 높이까지 입력하는 기능이 있습니다. 정확도가 아주 높은 것은 아니지만, 아무래도 안하는 것 보단 낫습니다. 주로 회로기판과 필드방향 구조상, 주로 위쪽 뚜껑에 민감하게 되므로 그 뚜껑의 높이를 어느정도 미리 예상하여 설계할 필요가 있는 것이지요.
결국 하우징 케이스는 외부 필드나 회로에 의해 영향받지 않도록 안정적으로 밀폐시키는 효과가 있는 것이므로, 그 내부에서 나가지 못해서 맴도는 필드가 성능을 깎아먹지 않도록 배려해야 하는 것입니다.
그리고 Dielectric Resonator라고 불리우는 유전체 공진기의 경우 역시 구조적인 공진에 가깝지만, 위의 cavity와는 원리와는 또 다릅니다. 공기와 다른 고유전율을 가진 유전체는, 어떻게 보면 내부가 공기로 되어 있는 air cavity의 크기를 축소해놓은 형태처럼 됩니다. 그렇지만 그런 금속 cavity와 크게 다른 점은, 외부의 필드를 받아서 공진시킬 수 있는 덩어리(bulk)라는 점입니다. 도파관 형태의 air cavity는 사방이 금속으로 막혀있기 때문에 동축선으로 벽에 구멍을 뚫어서 급전을 해야만 합니다.
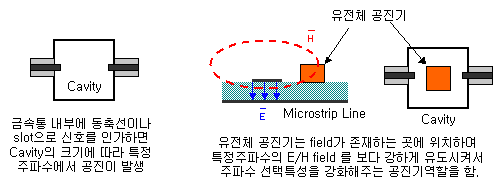
#유전체 공진기 역시 cavity와 마찬가지로 공진되는 E field와 H field coupling과 형상에 대해 여러 가지 공진 mode를 가지고 있으며, 그 자체로 복잡한 수학적인 개념이 매우 중요시되는 분야입니다. 고로 LC공진의 개념적 이해를 주로 설명하기 위한 본 글에서는 따로 다루지 않도록 하겠습니다.
공진에서의 Q값
공진에서의 Q(Quality factor)는 주파수 선택 특성품질을 의미합니다. 그 정의는 아래와 같습니다.

#공진주파수 점에서 양쪽으로 3dB, 즉 반으로 감쇄되는 지점의 주파수간의 차이를 소위 3dB 대역폭이라고 하는데,
공진주파수를 3dB 대역폭으로 나눈 것이 바로 Q값입니다. 즉 공진특성이 샤프할수록 3dB 대역폭은 좁아질 것이고,
결국 Q값은 커집니다.
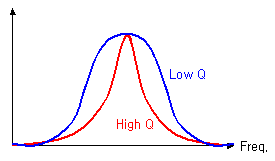
이것은 소위 circuit Q 라고 해서 회로에서의 대역폭과 관련된 개념입니다. 스미스차트 강의에서 회로의 Q에 대해 보셧겠지만, Q가 낮으면 대역이 넓다는 의미이고 높으면 협대역의 의미이지요.
공진이란게 결국 특정 주파수의 선택특성을 말하는 것이기 때문에, 얼마나 샤프하게 주파수를 선택해낼 수 있느냐?를 의미하는 지표가 결국 Q값인 것입니다. Q값은 대체로 높아야 좋은 경우가 많지만, 역으로 낮아야 할 경우도 있기 때문에 단순히 어떤 값이 좋다고 말할 수는 없습니다. 그보다는 Q값을 통해 어느정도의 선택도와 대역폭을 가졌는지를 감잡는게 중요합니다.
위에서 정의했던 대역폭의 Q값은 공진기에서 아래와 같은 수식으로 표현되기도 합니다.

이러한 Q값의 공식을 잘 보면, LC 말고도 R값이 포함되어 있습니다. 즉, 실제로 공진부만의 특성을 의미하는 것이 아니라 부하(R)가 걸린상태에서의 회로 Q값입니다. (loaded Q)
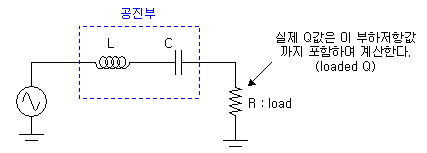
실제로 Q는 위에서 입출력 부하 RL 값에 따라 Q값의 계산이 바뀌게 됩니다. 그렇기 때문에 실제 최종적인 Q값이 어떻게 될지는 단순히 공진부만으로 결정되는 것이 아니라는 점이 문제가 됩니다. 그래서 부하가 걸린 상태의 Q (Loaded Q)값과 부하가 걸리지 않은 공진기만의 Q (Unloaded Q)값으로 분류가 되는 것입니다. Q에 대한 자세한 상세 공식들은 아무 초고주파 공학서적을 봐도 자세히 나오있으므로 정확한 유도과정과 수식은 책을 참고하시고, 여기서는 기본적인 개념을 잡으시기 바랍니다.
발진과 공진
초심자분들의 경우 발진과 공진을 혼동하는 경우를 종종 보게 됩니다. 우선 결론적으로 발진과 공진은 연관성은 있지만 그 자체는 전혀 다른 개념입니다.
발진이 뭐길래? 에서 보셨다시피 발진은 능동소자에서 feedback loop와 gain에 의해 발생하는 현상이고, 공진은 수동구조에서 특정 주파수만 민감하게 반응하는 어떤 현상을 말합니다. 굳이 두가지를 구분하는 표를 만든다면 아래와 같이 될 것입니다.
|
|
공진
|
발진
|
|
발생소자
|
수동소자
|
능동소자
|
|
원리
|
신호주파수와 전기적/구조적 주파수가 일치될 때 에너지가 집중됨
|
feedback loop가 gain을 가지면서 작은 잡음성 신호가 크게 성장해버림
|
|
현상
|
특정 주파수에 대한 선택 특성
|
발진조건이 성립되는 주파수에서 큰 신호전력이 샤프하게 나타남
|
|
DC 전원
|
필요도 없고 상관도 없음
|
있어야만 발진이 일어남
|
|
긍정적 용도
|
필터, 발진기의 공진부,
각종 주파수 선택소자
|
주파수 신호원
|
|
부정적으로
나타나는 경우
|
불필요한 spurious 발생
엉뚱한 주파수 선택특성
|
소자파괴, 시스템 불안정 및 수명감소
|
'생활속의 전기상식' 카테고리의 다른 글
| 2개 시설 전기안전관리자 통합 선임 가능 여부 (2) | 2025.01.24 |
|---|---|
| 인덕턴스 (Inductance)와 커패시턴스(Capacitance)의 개념 이해 (0) | 2023.02.12 |
| 입체각, 호도법 쉽게 이해하기 (0) | 2022.03.07 |
| 전기기사 단답형 암기자료 (0) | 2021.10.09 |

