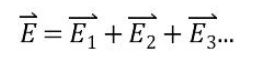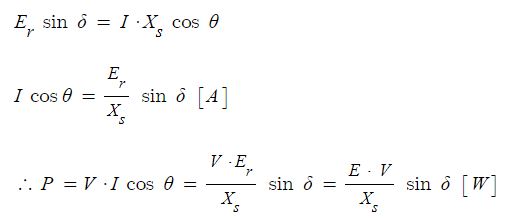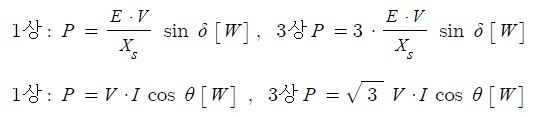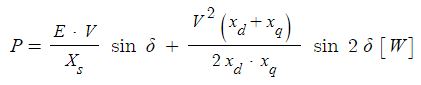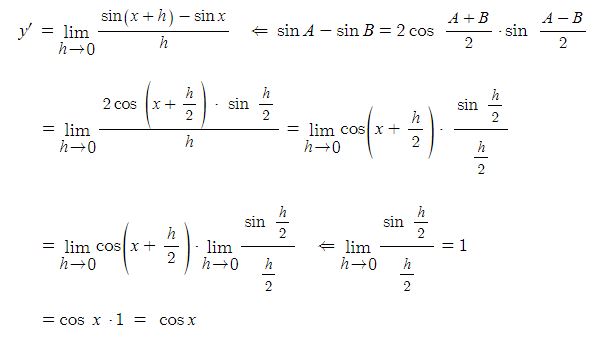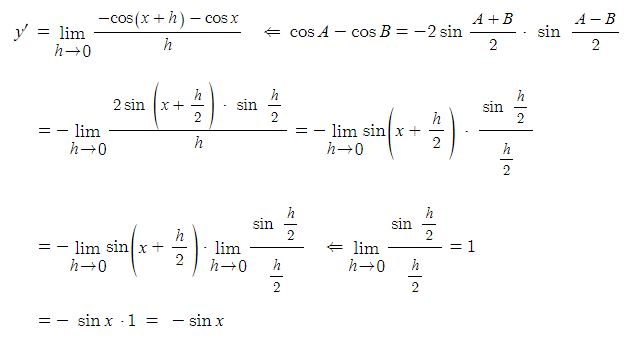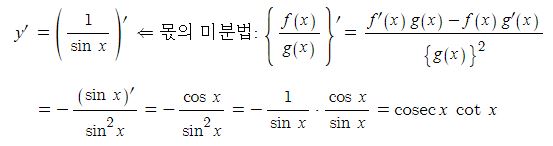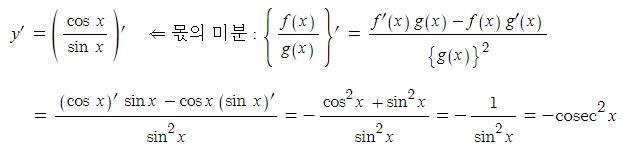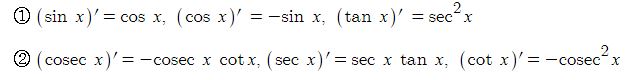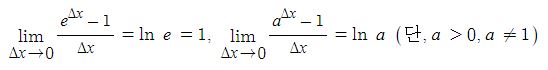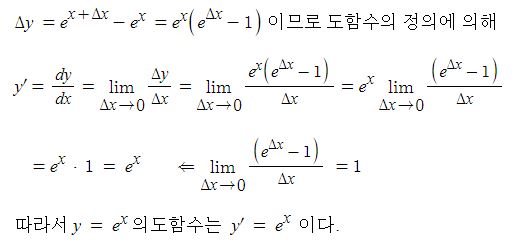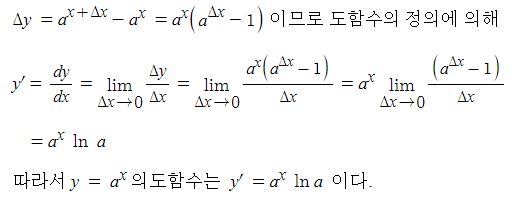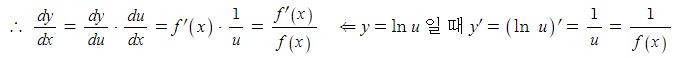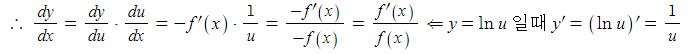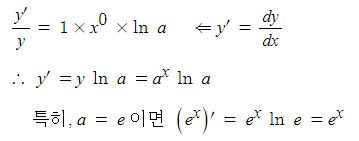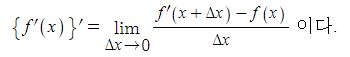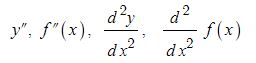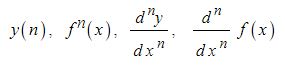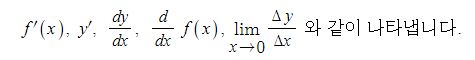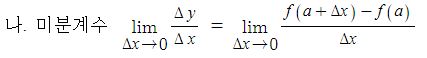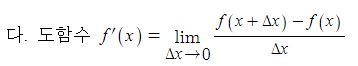아낌없이 주는 나무

전지의 중요한 특성인 용량, 에너지 밀도, 출력에 대해 알아 보자.

전지는 우리가 사용하는 전자기기에서 중요한 역할을 하죠.

이 특성들을 이해하면 전지의 성능을 파악하는데 도움이 됩니다.

​

1. 전지의 용량 (Capacity)​

​

전지 용량은 전지가 완전히 방전될 때 얻을 수 있는 전하량을 말해요.

전지 용량은 전류(I)와 시간(t)의 곱으로 계산됩니다.​

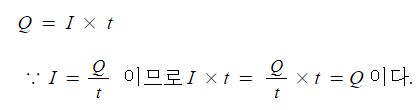
​2. C - rate

​

C-rate는 전지의 충전 및 방전 속도를 나타내는 지표에요.

예를 들어, 1C rate는 전지를 1시간 안에 완전히 충전 또는 방전하는 속도를 의미해요.

만약 2C rate라면 30분 만에 완전히 충전하거나 방전할 수 있는 속도를 뜻해요.

​

3. 에너지 밀도

​

​에너지 밀도는 전지에서 얻을 수 있는 에너지의 양을 나타내요.

전지의 성능을 결정하는 매우 중요한 인자입니다.

에너지 밀도는 단위 부피당 또는 단위 무게당 에너지로 나타낼 수 있어요.

​

전지의 에너지를 전압과 용량을 이용해 계산한 후, 이를 전지의 무게 또는 부피로 나누어 에너지 밀도를 구할 수 있습니다.

​

전지 용량이 Q =I × t 로 주어졌을 때, 에너지는 다음과 같이 계산됩니다:​

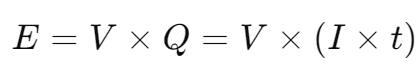
E 는 에너지 (와트시, Wh)

V 는 전지의 전압 (볼트, V)

Q 는 전지 용량 (암페어시, Ah 또는 밀리암페어시, mAh)

​

에너지 밀도가 높을수록 전지의 성능이 우수하다고 볼 수 있어요.

​

4. 출력 (Power)

​

출력은 전지가 단위 시간당 생산할 수 있는 에너지를 뜻해요.

출력 𝑃 전류 𝑖와 전지 전압 𝐸의 곱으로 나타낼 수 있어요.​

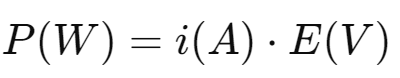
전지의 출력은 주어진 전압에서 얼마나 큰 전류를 흘려줄 수 있는가에 대한 척도가 되기도 해요.

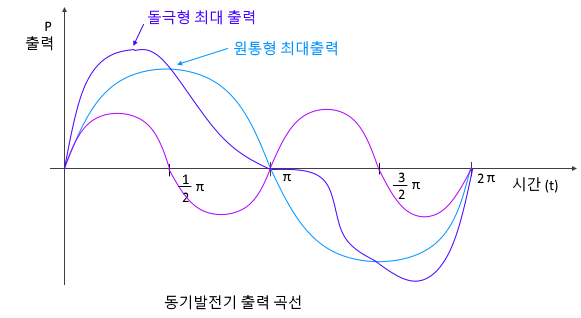
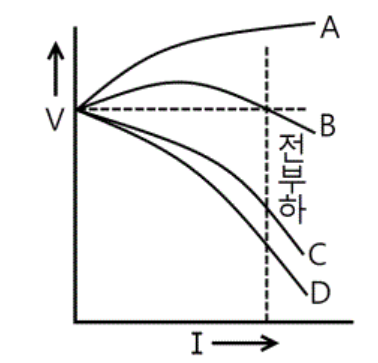
일반적으로 전류가 증가할 때 전지로부터 얻을 수 있는 출력은 초기에는 증가하다가 최고 값에 도달한 후 감소하는 경향을 보입니다.

이는 전류가 특정 값 이상으로 증가하면 전지 전압이 감소하기 때문이에요.

출력도 용량이나 에너지 밀도와 마찬가지로 단위 무게나 부피를 기준으로 하는 출력 밀도(power density)로 나타낼 수 있어요.

출력 밀도가 높을수록 전지의 성능이 좋다고 할 수 있어요.

​

5. 요약

​

전지 용량 (Capacity): 전지가 완전히 방전될 때 얻을 수 있는 전하량. 전류와 시간의 곱으

로 나타내며, 이론 용량과 실제 용량이 있습니다.

에너지 밀도 (Energy Density) : 전지에서 얻을 수 있는 에너지의 양. 단위 부피당 또는

단위 무게당 에너지로 나타내며, 전지의 성능을 결정하는 중요한 지표입니다.

출력 (Power): 전지가 단위 시간당 생산할 수 있는 에너지. 전류와 전압의 곱으로 나타

내며, 전지의 효율성과 관련이 깊습니다.

​

#에너지 #밀도 #전류 #전압 #출력

가우스의 법칙은 독일의 수학자 칼 프레드리히 가우스가 1867년 발표한 전기력학의 기초라고 할 수 있다. 이 법칙은 대칭성을 가진 전하분포상에서 전기장을 구하는데 아주 유용하게 쓰인다.

전기력의 세기를 구하거나 전기장을 정의할 수 있는 공식 중의 하나인 쿨룽의 법칙이 있는데 이 쿨룽의 법칙은 모든 전기력을 구하는데는 한계가 있다. 쿨룽의 법칙은 '점전하 (point charge)를 가정하여 전기력을 구한다. 그런데 현실에서는 전기력이 점전하 뿐만 아니라 다양한 형태로 존재하고 이런 전기력을 구하는데에는 쿨룽의 법칙은 한계가 있다.

일상에서는 위 그림 처럼 원형, 육각형, 사각형 등의 다양한 형태의 크기와 넓이를 가진 물건들이 많은데 크기를 고려하지 않는 쿨룽의 법칙으로는 이들의 전기력, 전기장을 계산하기가 힘들다. 이런 것들의 전기장을 구하려면 적분을 통해 이 물체의 전하분포를 엄청 잘게 잘라서 점전하급으로 잘게 나눈 후, 그 점전하들의 전기장을 합하여 계산할 수 있지만 전기장은 크기 뿐만 아니라 방향도 가지고 있어 계산이 매우 어렵게 된다.

위 식과 같이 매우 복잡한 계산을 해야 한다.

​

위와 같은 복잡한 계산 식을 사용하지 않고 전기장을 쉽게 구하기 위해 나온 계산식이 바로 '가우스의 법칙'이다. 그러나 가우스의 법칙도 선, 구, 면 처럼 전하의 분포가 대칭성을 가지는 경우에만 적용이 가능하지만 적어도 대칭성을 가진 전하분포일 때 전하를 구하는 방식은 가우스 법칙하나만으로 아주 간단하게 구할 수 있다.

​

가우스의 법칙은 무엇일까 ?

위 식은 가우스의 법칙을 나타낸 식이다.

이를 우리말로 표현을 하면 '임의의 폐곡면 (가우스면)을 통과하는 전기선속은 폐곡면내의 총 전하량에 비례한다'라고 할 수 있다. 이말은 어떤 의미일까 ? 상세히 알아 보자.

​

1. 전기선속 (electric flux)이란 ?

위 그림처럼 넓이가 A인 사각형 단면을 전기력선이 통과하고 있다고 가정해 보자. 전기력선의 밀도는 전기장의 크기에 따라 달라지는데 그렇다면 단면 A를 지나가는 전기력선의 갯수는 E × A 에 비례한다. 이것을 '전기장 다발' 혹은 '전기력선속'으로 부르며 electric flux 라고 하며 기호로는 ф 대문자 파이 (phi)로 나타낸다.

그런데 위 그림에서 처럼 맨 앞 그림은 단면이 전기력선속과 수직으로 되어 있지만 경우에 따라서는 가운데 그림처럼 비스듬하게 놓여 있을 수도 있고 극단적으로 면이 수평으로 누워있을 수도 있다. 그렇다면 전기력선과 단면이 수직인 경우에 비해 전기력선이 단면에 통과하는 경우에 통과하는 양이 적어지므로 전기선속 Φ = EA cos θ 로 구하게 된다. 즉, 전기선속은 단면과 전기력선속이 수직일 때 제일 크고, 수평일 때 가장 작다.

그렇다면, 단면이 아닌 닫힌 곡면, 즉, 폐곡면의 경우를 살펴보자. 위 그림과 같이 구체 모양인 곡면의 정중앙에 양전하 q가 있다고 하자. 이 양전하 q가 뿜어내는 전기장에 의해 구체 표면으로 빠져 나가는 전기선속을 구하려면 곡면을 잘게 나누어서 잘게 나눈 면의 전기장을 구한 다음 각각의 전기장을 합하면 될 것이다. 이를 수식으로 나타내면 다음과 같다.

위와 같이 전기장 (방향을 가진 벡터값)과 면적벡터를 폐곡면에서 모두 적분을 하면 되지만 이는 계산하기 매우 까다롭다.

​

2. 점전하에 대한 가우스 법칙

그렇다면 점전하 q가 반지름이 R(=r)인 구의 중심에 잇다고 가정을 하자. 쿨룽의 법칙에 의하면 전기장의 크기는 다음과 같이 구할 수 있다.

구의 표면적은 4πr2 이므로 가우스면 (폐곡면)을 일컫는 dA = 4πr2 이 된다. 이를 식으로 표현하면 다음과 같다.

여기서 알수 있는 중요한 사실은 구체의 반지름 r이 어떻게 되든 전기선속의 값에는 아무런 영향을 주지 않는다는 것이다. 결국, 전기선속의 값은 입실론 (ε)의 값도 정해져 있으므로 가우스면 내부의 '총 전하량'에만 영향을 받는다는 것을 알 수 있다.

만약에 점전하 하나가 위 그림의 S1이라는 폐곡면의 중심에 있는데 폐곡면이 만약 구체 형태가 아닌 S2, S3와 같이 찌그러진 곡면이라고 하면 이 때 폐곡면에서 나가는 전기력선의 수가 달라질까 ? 위의 오른쪽 그림만 보아도 그렇지 않다는 것을 쉽게 알 수 있다. 결국 가우스면 이기만 하면 곡면의 반지름과는 상관없이 총 전하량에 의해서만 전기력선속이 정해진다는 것을 그림으로 알 수 있다.

결국 폐곡면이기만 하면, '임의의 폐곡면(가우스면)을 통과하는 전기선속은 폐곡면 내의 총전하량에 비례한다'는 법칙이 성립하는데 이것이 바로 전자기학에서 말하는 가우스 법칙 (Gauss's law)이다.

​

※ 주의

⊙ 가우스 법칙에서 가장 오른 쪽 Q는 가우스면 내부의 알짜 전하량을 의미하나 E는 가우스면 내외부의 전체 전기장임을

     염두에 두어야 한다.

⊙ 전기선속이 "0"이면 전기장도 "0"이다. 아니다.

     가우스 법칙은 전기선속이 폐곡면 내부의 알짜 전하량에 비례한다는 것이지, 전기장이 폐곡면 내부의 알짜 전하량에

     비례한다는 것이 아니다.

가우스 법칙은 대칭성을 가진 전하 분포에 대한 전기장을 계산할 때 아주 유용하게 쓰이는데 이를 구하려면 가우스 법칙만으로는 계산이 어렵고 대칭성을 이루는 형태 (구, 원통, 평면 등)에 대한 '표면전하 밀도'를 알고 있어야 계산이 가능하다.

​

#가우스 #폐곡면 #전기력선속 #전기력선 #점전하 #쿨룽 #알짜 #전기장

1. 전기장이란 ?

전기장 (Electric field)은 '어느 하나의 전하가 전기적인 힘을 미치는 공간'이라고 할 수 있다. 다시 말하면 어느 공간에 하나의 전하를 놓으면 주위에 있는 다른 전하에게 영향을 미치는 성질이라 할 수 있다. 여기서 '장(field)'에는 전기장 뿐만 아니라 중력장, 자기장 등도 있는데 예를 들어 자석에 쇠구슬을 서서히 다가가게 하면, 어느 일정한 거리에 도달하는 순간 자석이 쇠구슬을 끌어 당기면서 자석에 붙게 된다. 이는 자석이 가진 힘이 미치는 공간, 즉 장(field)에 쇠구슬이 진입했기에 쇠구슬이 자석의 힘의 영향을 받게 된 것이다.

이 예를 통해 '장(field)'이란 비접촉력을 설명할 때 사용하는 용어라는 것을 알 수 있다.

전기장도 마찬가지로 하나의 전하의 힘이 이웃한 전하에게 영향을 미치는 영역을 말한다.

위 그림에서 원전하 Q의 근처에 임의의 시험전하 q가 들어 왔다고 가정을 해 보자.

Q와 q가 모두 양전하라면 Q와 q는 서로 척력을 발생시키며 반발할 것이다. 그러면 반발력이 Q와 q가 서로 맞닿아 있을 때만 발생하는가 ? 그건 아니다.

전기장 (Electric field)이라는 성질은 공간적으로 떨어져 있는 곳에도 영향을 미친다는 의미가 포함되어 있으므로, Q와 q는 일정한 거리에 접근하는 순간 Q의 전기장에 의해 서로 닿지도 않았는데 반발력이 발생하게 된다. 만약에 Q는 양전하이고 q는 음전하라면 Q의 전기장내에 q가 들어서면 서로 끌어 당기는 인력이 발생할 것이다.

이러한 전기장을 식으로 표현할 때 E (전계의 세기)로 표현하며, 전기장을 알고 있을 때 전기력을 구하는 식은 다음과 같다.

이와 같이 전기장을 알게 되면 전기장 내에 있는 전하가 받는 힘의 크기와 방향도 알 수 있게 된다. 다시 말하면 전기장 (전계의 세기) E는 시험전하 q가 Q의 전기장 내에서 전기력을 받는 세기라고 할 수 있다.

Q와 q가 점전하라고 한다면 전기력은 쿨룽의 법칙에 의하여 구할 수 있고, 이 식에서 전기장 (전계의 세기)을 구하는 식을 유도할 수 있다. 위 식에서 결국 전기장을 구하는 식은 쿨룽의 법칙, 전기력을 구하는 식에서 시험전하의 전하량 q를 빼면 된다.

​

위 식에서 이 전기장에 대하여 하나 덧붙이면, 전기장이 균일하게 분포되어 있다고 가정하면 전하량이 q이고 질량이 m인 입자를 균일한 전기장 E 내에 놓았을 때의 입자가속도를 구할 수 있게 된다.

※ 전기력 F는 단지, 힘의 종류 중에 하나이므로 뉴턴의 운동법칙 F = ma 의 식을 적용할 수 있다.

위와 같이 F = ma 를 이용하여 균일한 전기장 E 내에 위치한 전하 q, 질량 m인 입자의 입자 가속도를 구하는 방정식을 유도해 낼 수 있다. (단, 균일한 전기장일 때 입자에 작용하는 전기장이 일정하여 등가속도 운동임을 특정할 수 있다)

​

2. 전기력선이란 ?

​

전기력선 (Electric field lines)은 '전기장을 눈에 보이게 선으로 그려 놓은 것'이라 할 수

있다. 전기장을 형성하는 전기력선의 벡터를 선으로 이어 놓은 것이라 할 수 있다.

양전하, 음전하이냐를 떠나서 모든 전하는 자신만의 전기장을 갖게 되는데, 이 전기장은 눈에 보이지 않으므로 전기장이 미치는 범위와 형태를 선으로 표현하면 이해하기가 쉽게 된다. 가장 기본적인 전기력선은 위 그림처럼 양전하와 음전하의 전기장을 표현하는 것인데 음전하는 화살표가 안쪽으로 양전하는 화살표가 바깥쪽으로 향하게 된다.

이 때 전기력선의 규칙은 다음과 같다.

  ⊙ 전기장 벡터 E는 각 점에서 전기력선의 접선방향이다.

  ⊙ 전기력선은 양전하에서 나와서 음전하로 들어간다.

  ⊙ 전기력선은 서로 교차하지 않는다.

이러한 규칙에 따라 전기력선은 위 그림과 같이 다양한 형태로 나타난다. 전하 하나만 독립적으로 존재하거나, 같은 극성을 같는 전하가 이웃할 때, 다른 극성을 갖는 전하가 이웃할 때 등 전기력선이 나타는 모양을 각각 다르게 된다.

전기력선은 단순히 방향만을 알려 줄 뿐만 아니라 전기력선이 어떻게 분포되어 있느냐에 따라 전기장의 세기도 가늠할 수 있다. 전기력선이 듬성듬성 분포한 곳은 상대적으로 전기장이 약한 곳이며, 전기력선이 촘촘히 분포한 곳은 전기장이 상대적으로 강한 곳이다.

​

그런데 지금까지는 전하가 각각 하나씩 존재하는 경우를 가정했는데 현실 세계에서는 전하가 하나의 공간에 무수히 많이 존재하게 된다. 한 공간에 전하가 무수히 많이 존재하게 되면 각 전하가 가진 전기장이 서로 중첩될 수 있는데 이럴 경우 특정지점의 전기장 E는 그 주변에 존재하는 무수한 전하들의 전기장들의 벡터합으로 표현할 수 있다. 이를 중첩의 원리라고 하며 식으로 표현하면 다음과 같다.

#전기장 #전계의세기 #전기력선 #자기장 #전하

동기발전기의 출력에 대하여 알아 보자.

​

동기발전기의 발전원리는 직류발전기와 원리에 같다.

위 그림과 같이 자석(계자)에서 자속이 발생하여 자계를 형성된 상황에서 코일, 즉 도체가 자속을 끊게 되면 도선에 페러데이의 왼손법칙과 렌츠의 법칙에 따라 유기기전력이 발생하게 된다. 이 때 도체(코일)은 자속을 끊는 역할을 하는 코일변과 자속을 끊지 않는 코일단으로 나누게 된다. 도체에 유기기전력이 발생하면 도체 주위에 자기장이 형성되는데 이는 주자속에 영향을 주게 되며 이를 전기자 반작용이라고 한다. 코일변에서는 전기자 반작용을 일으키고 코일단에서는 전기자 반작용이 발생하지 않는다. 따라서 코일변은 전기자 반작용 리액턴스Xa라고 하고 코일단에서는 누설리액턴스 (Xℓ)이라고 한다. 이들과 코일(도체)의 고유저항 (ra)이 합쳐 발전기의 임피던스(Zs)을 구성하게 된다.

Zs = ra + (Xa + Xℓ) = ra + Zs

동기 발전기는 3상 발전을 한다. 3상 발전기는 a, b, c 상 3상의 코일이 120˚ 간격으로 자속을 끊어 유기기전력을 발생한다. 3상 동기발전기는 Y결선을 한다. Y결선을 하면 각 상의 전압을 낮추어 절연에 유리하고 각 상에 제3고조파가 발생하지 않는 이점 등이 있다.

3상 동기발전기는 a, b, c상 각상에서 유기기전력이 발생하나 출력을 분석하기 위해서 한개의 상을 기준으로 하여 분석을 하게 된다. 앞에서 말한 바와 같이 동기발전기의 경우 코일의 내부저항, 전기자 반작용 리액턴스, 누설리액턴스가 모여 전체 임피던스를 구성하는데 아래 그림에서 보는 바와 같이 저항 r, 리액턴스는 발전기 내부에서 발생하나 표기는 선로에 표기하는 것으로 약속한다.

위 그림은 3상 동기발전기의 a상만을 등가회로로 나타낸 것이다. 발전기의 임피던스에 의해 전압강하가 발생하게 되어 유기기전력은 다음과 같이 표현할 수 있다.

E = V + I · Zs

발전기의 출력을 부하전력을 이용하여 구해보자.

부하의 전력 P = VI cos θ 로 나타낼 수 있다.

이를 이용하여 발전기의 출력 P를 아래의 벡터도를 보면서 구해보자.

위 [그림1]에서 처럼 발전기의 유기기전력 Er 발생한다고 하자. 이 유기기전력이 저항(r)과 리액턴스(Xs)을 흐르면서 전압강하를 일으키게 되는데 저항(r)에 흐르는 전류와 전압과는 θ 만큼의 위상차가 있다고 하자. 저항에서 발생하는 전압강하(IR)는 저항에 흐르는 전류와 위상이 같게 된다. 한편 리액턴스에 흐르는 전류는 전압보다 90 ˚ 늦게 되는데 거꾸로 말하면 리액턴스 전압(IX)는 전류 보다 90 ˚ 앞서게 된다.

이를 종합하면 Er = V +IR + IX가 된다.

그런데 [그림2]에서 보는 바와 같이 코일에 흐르는 전류에 의한 임피던스는 대부분 리액턴스로 구성되고 저항성분의 극히 미미하다. 따라서 발전기에서 저항성분에 의한 전압강하는

거의 없다고 보아도 무방하다. 따라서 벡터도에서 저항강하 (IR)은 삭제하여도 무방하다.

[그림 3]을 보면 발전기에서 전압강하는 대부분 리액턴스(IX)로 구성되므로 임피던스와 리액턴스가 같다고 보아도 무방하다. 실제 약간의 차이는 있을 수는 있으나 실용상 같다고 하자. 따라서 IZ = IX로 표현할 수 있고 유기기전력 Er과 전류 Ir의 위상차 θ와 IX와 수직선과의 분리각 θ 거의 같다고 할 수 있다. 따라서 수직선의 길이는 Es sin δ와 IX cos θ로 나타낼

수 있다.

즉 Es sin δ = IX cos θ 이다.

​

위와 같은 내용을 기반으로 발전기의 출력을 알아 보자.

다시 등가회로로 돌아가서 동기발전기에서 발전기에서의 출력은 발전기에서 발생한 유기기전력이 발전기 내부의 저항과 리액턴스 등 임피던스에 의한 전압강하가 반영된 실제 부하에 전달되는 일할 수 있는 능력 P[W]를 말하는 것으로

P = V · I cos θ 로 나타낼 수 있다.

위 벡터도를 이용하여 동기발전기의 출력식을 유도해 보자.​

그런데 위식은 한상을 기준으로 한 계산식이다. 3상으로 하며 상전력은 3배를 하면 되고

선간전압을 기준으로 하면 √3 V · I cos θ 가 된다.​

위 식은 동기발전기 중에서 원통형 발전기에만 성립을 한다. 돌극형의 경우에는 단절계수(xd)와 분포계수 (xq)를 적용하여 다음과 같은 산식이 성립한다.​

원통형 동기발전기는 sin 파형을 형성하므로 최대출력은 90 ˚에서 형성되나 돌극형의 경우에는 sin 파형과 사인 2고조파형이 합성되므로 최대출력은 60 ˚에서 형성된다.

이상의 내용으로 동기발전기의 출력 관련 내용을 정리하면 다음과 같다.

#부하각 #상차각 #동기발전기 #출력 #위상차 #임피던스 #리액턴스 #전압 #앞선전류

#지상전류 #진상전류 #전압강하 #원통형 #돌극형 #최대출력 #동기발전기 #전기자반작용 #누설리액턴스

수하특성(정전류 특성)이란 ?

​

수하특성이란 부하(전류)가 증가하면 내부저항이나 전기자 반작용 등으로 이하여 전압강하가 발생하고 전압강하는 전류를 감소시켜 일정한 전류를 유지시켜 주는 현상을 말한다.

​

수하특성은 용접기 등에서 주로 사용되는데

아크(arc) 용접의 경우, 용접작업은 저전압의 고전류를 사용하여 용접을 하게 되는데

처음 용접을 할 때는 어느 정도 높은 무부하 전압을 사용하게 되는데

처음 아크(arc)가 발생하게 되면 부하전류가 증가하게 되면서 단자전압이 낮아지게 되는데

이러한 현상을 수하특성이라고 한다.

​

수하특성은 영어로 Drooping characteristic 이라고 하는데 여기서 Drooping이란 아래로 처진다는 뜻으로 전류(부하)가 증가하면 전압이 떨어지는 의미로 볼 수 있다.

​

수하특성은 정전류 특성이라고도 하는데 용접기에서 수하특성을 갖게 되면 아크(Arc)전압이 다소 변하하여도 용접전류은 극히 작은 변화만 발생하게 되는데 따른 명칭이다.

​

수하특성을 갖게 되면 어떠한 요인에 의해 전류가 변화하여도 전류는 즉시 다시 원래의 상태로 돌아오게 되는 특성을 갖게 된다. 따라서 아크(Arc) 용접에서와 같이 일정한 아크용접을 유지하기 위한 중요한 특성중에 하나가 된다.

​

위 그림에서 곡선 C, D에서는 전류가 증가하면 전압이 감소함을 볼 수 있다.

곡선 C,D가 수하특성을 보여준다고 하는데 발전기에서 수하특성을 알아 보자

  ① 부하증가 (부하전류 증가 : 부하는 병렬로 연결하므로)

  ② 부하전류 증가 : 발전기 전기자 반작용 증가 (반대 자속 증가)

  ③ 전기자 반작용 증가 : 전체 자속 감소

  ④ 전체 자속 감소 : 유기 기전력 감소

  ⑤ 기전력 감소 : 단자전압 감소

  ⑥ 단자전압 감소 : 부하전류 감소

​

이를 건전지를 예로 들어 설명하면 다음과 같다.

위 그림에서 건전지에서 부하하나에 연결하면 전류가 작게 흐르다가 부하 2개를 병렬로 연결하면 전류가 2배로 흐르게 되고 전류가 많이 흐르게 되면 내부저항에 의해 전압강하가 많아지게 되어 단자 전압은 낮아지게 된다.

​

#수하특성 #정전류특성 #발전기 #용접기 #전압강하 #전류 #전기자반작용

삼각함수의 덧셈 또는 뺄셈을 곱셈으로 고치는 공식과 삼각함수의 극한을 이용하여 삼각함수의 도함수를, 지수함수와

로그함수의 극한을 이용하여 지수함수와 로그함수의 도함수를 구하는 방법을 알아 보자. 또한 이계도함수의 정의와

이계도함수의 계산법도 알아 보자.

​

1. 삼각함수의 도함수

삼각함수의 도함수를 구하려면 임의의 점에서의 미분계수를 구하면 되는데 삼각함수의 극한을 구할 수 있다.​

가. 삼각함수 y = sin x, y = cos x, y = tan x 의 도함수는 도함수의 정의와 삼각함수의 극한, 삼각함수의 합 또는 차를

      곱으로 변환하는 공식을 이용하여 구할 수 있다.

① y = sin x 의 도함수​

따라서 (sin x)' = cos x 이다.

​

② y = cos x의 도함수​

따라서 (cos x)' = - sin x 이다.

​

③ y = tan x 의 도함수​

   따라서 (tan x)' = sec2 x 이다.

​

나. 삼각함수 y=cosec x, y = sec x, y = cot x 의 도함수도 바로 위에서 구한 세 삼각함수의 도함수와 몫의 미분법을

      적용하여 구할 수 있다.

① y = cosec x 의 도함수​

② y = sec x 의 도함수​

   따라서 (sec x)' = sec x · tan x 이다.

③ y = cot x 의 도함수  ​

【 삼각함수의 도함수】​

2. 지수함수의 도함수

지수함수 y = e^x, y = a^x 의 도함수는 도함수의 정의와 지수함수의 극한을 이용하여 구할 수 있다.​

가. y = e^x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

나. y = ax (a >0, a ≠ 1) 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

참고로 합성함수의 미분법을 이용하여 y = ex 의 도함수를 구할 수 있다.​

3. 로그함수의 도함수

로그함수 y = ln x, y = log ax (a >0, a ≠1)의 도함수는 도함수의 정의와 무리수 e의 정의에 의하여 구할 수 있다.​

가. 로그함수의 도함수

y = ln x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 한다면

△y = ln (x+△x) - ln x 가 되므로 도함의 정의에 의해​

또한 로그의 성질 log ax = ln x / ln a (a >0, a≠1)를 이용하면 다음과 같이 y =log ax 의 도함수를 구할 수 있다.​

나. 절대값을 포함한 로그함수의 도함수

미분가능한 함수 f(x)에 대하여 f(x) > 0 또는 f(x) <0 인 경우에 ln lf(x)l 의 도함수를 구해 보자.

① f(x) > 0 일 때, lf(x)l = f(x)이므로 u = f (x)로 놓으면 y = ln u​

② f(x) < 0 일 때, lf(x)l = -f(x)이므로 u = -f (x)로 놓으면 y = ln u​​

【 로그함수의 도함수 】​

따라서 ①, ② 를 정리하여 보면​

4. 로그 미분법

가. 로그 미분법

밑과 지수에 모두 변수를 포함하는 지수형태의 함수나 복잡한 분수함수의 도함수를 구하기 위해서는 양변에 로그를

취한 후 합성함수의 미분법이나 음함수의 미분법을 적용하면 된다.

이런 방법을 로그미분법이라고 한다. 이때 로그의 진수가 양수이어야 하므로 로그를 취하기 전에 식의 양변에 절대값을

먼저 취한 다음 로그를 택해야 한다. 만약 이미 양변이 양수일 때는 절대값을 취하지 않아도 된다.​

몫의 미분법과 합성함수의 미분법을 적용하면 도함수를 구할 수 있지만 식이 매우 복잡하므로 로그를 취한 후 음합수

미분법을 이용하여 도함수를 구하는 것이 보다 빠르고 쉽다.

양변이 모두 양수이므로 식의 양변에 자연로그를 취하여 로그의 성질을 이용한다.​

즉, 함수 y = f(x) 에서 f(x)의 형태가 일반적인 미분법을 적용하기에 복잡한 형태라면 로그미분법을 이용해서

다음 순서에 따라 함수의 도함수를 구할 수 있다.

【 로그 미분법 】

복잡한 지수와 몫으로 표현된 함수는 로그미분법을 이용하여 도함수를 구할 수 있다.

① 양변에 절대값을 취한다. ⇒ ㅣyㅣ= l f(x)ㅣ

② 양변에 자연로그를 취한다. ⇒ ln ㅣyㅣ = ln l f(x)ㅣ​

나. y = xa 의 도함수 (단, a는 실수)

자연수 지수에서 부터 유리수 지수까지는 함수 y = x'의 도함수가 y'=r xr-1 이다.

이제 로그미분법을 이용하여 a가 임의의 실수일 때, 함수 y = xa의 도함수를 구해 보자.​

【 로그 미분법의 활용 】

가. 지수함수 y = ax (a > 0, a ≠ 1)의 도함수를 로그미분법을 이용하여 구해 보자.

      y = ax 의 양변에 자연로그를 취하면 ln y = ln ax = x ln a

      양변을 x에 대하여 미분하면​

   위 식은 지수함수를 미분해서 얻은 도함수와 그 결과가 일치한다.

나. 이번에는 y =af(x) 의 도함수 (a>0, a≠1)를 로그미분법을 이용하여 구해 보자.​

   이 또한 지수함수를 포함한 합성함수의 도함수와 그 결과가 일치한다.

​

5. 이계함수

함수 y = f(x) 의 도함수 f'(x)가 미분가능하면 f'(x)의 도함수는 다음과 같다.​

이 때, f'(x)의 도함수를 함수 f(x)의 이계 도함수라고 하고 기호로는 다음과 같이 나타낸다.​

즉, 이 이계도함수는 어떤 함수를 두번 미분한 함수이다.

일반적으로 자연수 n 에 대하여 함수 y = f(x)가 n번 미분가능한 함수일 때 y = f(x)를 n번

미분하여 얻은 함수를 y = f(x)의 n계도함수라고 하고 기호로는 다음과 같다.​

【 이계 도함수 】

함수 y = f(x)의 도함수 f'(x) 가 미분가능할 때, f'(x)의 도함수를 y = f(x)의 이계도함수라

하고 기호로는 다음과 같이 나타낸다.​

#삼각함수 #도함수 #미분 #미분계수 #지수함수 #합성함수 #극한 #미분법 #평균변화율

#로그함수 #절대값 #로그미분법 #이계도함수

두 함수를 몫으로 표현된 함수, 합성함수, 음함수, 역함수, 매개변수로 표현된 함수 등

다양한 형태의 함수의 미분법에 대하여 알아 보자.

​

1. 몫의 미분법

가. 몫의 미분법​

위 함수는 도함수의 정의를 이용하여 다음과 같이 풀이할 수 있다.​

위와 같이 매번 도함수의 정의를 이용하여 도함수를 구하는 것은 복잡하고 시간이 많이

걸리게 되는데 몫의 미분법은 결과를 공식화하여 기억하자.​

[예제] 몫의 미분법을 이용하여​

【 몫의 미분법 】

두 함수 f(x), g(x) (g(x) ≠ 0)가 미분가능할 때

이와 같이 몫의 미분은 결과 공식을 외워 두자.​

n이 자연수일 때 다항함수 y = xn 의 도함수가 y' =n xn-1 이다. 그런데 몫의 미분법을 이

용하면 n이 정수일 때도 위 사실이 성립함을 알 수가 있다.​

①,②,③에서 알 수 있듯이 n이 양수일 때 뿐만 아니라 0이거나 음의 정수일 때에도 함수

y = xn 의 도함수 y' = n xn-1 이 된다. 즉, 임의의 정수 n에 대하여 y = xn 의 도함수는

y' = n x n-1 이 된다.

​

【 y = xn 의 도함수 (단, n은 정수) 】​

2. 합성함수의 미분법

가. 합성함수의 미분법

함수 y = (2x -3)3 의 도함수를 구하려면 다음과 같이 식을 전개한 후 미분해야 한다.​

이 처럼 다항함수의 차수가 조금만 높아도 전개한 다음 미분하는 것은 여간 복잡한 것이 아니다.

따라서 함수를 전개하지 않고 미분할 수 있는 방법이 있다면 그 방법을 이용하는 것이 빠르고 계산과정도 간단하다.

합성함수의 도함수가 어떻게 나타나는지를 확인해 보면 그 방법을 구체적으로 확인할 수 있다.

두 함수 y = f(u), u = g(x) 가 미분 가능할 때, 도함수의 정의를 이용하여 합성함수

y =f (g(x))의 도함수를 구해 보자.​​

위 식에서 앞, 뒤 두 극한 값을 찾으면 함성합수의 도함수를 구할 수 있다.

① 앞 함수의 극한 값

g(x+h) = B, g(x) = A 라고 하면 함수 y = g(x)미분 가능하므로 연속이다.

따라서 h → 0 일 때, g(x+h) → g(x) 이므로 h → 0 이면 B → A 이다.​

② 뒤 함수의 극한값은 도함수의 정의에 의해 g'(x)가 된다.

따라서 ①, ② 에 의해 합성함수 y = f(g(x))의 도함수는 다음과 같다.​

[예제] 함성합수의 미분법을 이용하여 함수 y = (2x-3)3의 도함수를 구해 보자.

이 함수를 f(u)=u3 과 g(x) = 2x-3의 합성합수라고 하면​

[합성함수의 미분법]​

【 합성함수의 미분은 (겉미분) × (속미분)】

합성함수 y = f(g(x))의 도함수를 다음과 같이 기억하자.

① 바깥 쪽 함수 f(x)를 미분하고 안의 함수 g(x)는 그냥 둔 다음 ☜ 겉미분 f'(g(x))

② 안쪽 함수 g(x)를 미분하여 ☜ 속미분 g'(x)

③ 겉미분과 속미분을 곱한다. ☜ f'(g(x)) · g'(x)

위 사실을 적용해 보면​

3. 매개변수로 표현된 함수의 미분법

x = t - 1, y = t2 + 1 과 같이 변수 t에 대한 함수 x, y가 주어져 있을 때, 함수 x, y를 각각

t에 대한 한수로 볼 수 있지만 중복되는 변수 t를 소거하여 y를 x에 대한 하나의 함수로 볼

수도 있다. 즉, x = t-1 에서 t = x+1 이므로 이를 y = t2 + 1에 대입하여 변수 t를 소거하면​

따라서 y는 t에 대한 함수이기도 하지만 x에 대한 함수이기도 하다.

이와 같이 두 변수 x, y의 함수 관계가 변수 t를 매개로 하여 x = f(t), y = g(t)의 꼴로 표현

될 때, 변수 t를 매개변수라 하고 x = f(t), y = g(t)를 매개변수로 표현된 함수라고 한다.

매개변수로 표현된 함수 x = f(t), y = g(t)의 도함수를 구하기 위해서는 매개변수 t를 소거

하여 y = f(x) 꼴의 함수로 고친 다음 미분해야 한다.​

함수 x = f(t), y = g(t)가 t에 대하여 미분가능하고 f(t) ≠ 0이면 x=f(t)의 역함수가 존재하고 t는 x의 함수이므로

y = g(t)도 x의 함수로 볼 수 있다.

따라서 t의 증분 △t에 대한 x의 증분을 △x. y의 증분을 △y라 하면 △x→0 일 때 △t→0 이고,​​

【 매개 변수로 표현된 함수의 미분법】

x = f(t), y = g(t) 가 t에 대하여 미분가능하고 f'(t) ≠ 0 이면​

예제 : 매개변수로 표현된 함수의 미분법​

4. 음함수의 미분법

가. 음함수의 미분법

일반적으로 함수는 정의역의 원소 x와 공역의 원소 y 사이의 관계식으로 표현할 수 있다.​

왼쪽과 같이 y = f(x)의 꼴일 때 y를 x의 양함수(Explicit function)라고 하고, 오른쪽과 같이 f(x,y) = 0 의 꼴일 때

y를 x의 음함수 (Implicit function)라고 한다.

음함수 f(x,y) = 0 을 양함수 y = f(x)의 꼴로 고칠 수 있다면 양함수로 변형한 다음 미분하여 도함수를 구할 수 있다.

하지만 음함수 x3+y2+2y+3 = 0 처럼 양함수로 고치기가 어려운 함수들에 대하여 음함수를 양함수 y = f(x)의 꼴로

고치지 않고 바로 미분할 수 있는데 이를 음함수의 미분법이라고 한다.

양함수든 음함수든 미분계수와 도함수는 모두 정의역의 원소인 x의 변화량에 따른 함수값 y의 변화량의 극한을 뜻하는

것이고 이것을 dy/dx라는 기호를 써서 나타낸다. 음함수는 비록 f(x,y) = 0 의 형태를 띠고 있다고는 하지만 y가 x에 대한

함수라고 가정을 한다.

따라서 문자 y를 포함하고 있는 항을 x에 대하여 미분할 때에는 y를 x의 함수로 보고 합성함수의 미분법을 적용하여

미분하는 것이 음함수의 미분법의 핵심이다.

음함수 x2 + y2 = 1 에 위의 사실을 적용해서 양변을 x에 대하여 미분하면​

[예제] 음함수의 미분법을 이용하여 x3+y2+2y+3=0 의 도함수를 구해 보자.

양변을 x에 대하여 미분하면​

【음함수의 미분법】

x의 함수 y가 음함수 f(x, y) = 0 의 꼴로 주어졌을 때, y를 x의 함수로 보고 각 항을 x에 대하여 미분하여 dy/dx를 구한다.

예제 : 음함수의 미분법을 이용하여 xy = 4 의 도함수 dy/dx를 구하여라.

[풀이] y를 x의 함수로 보고 각 항을 x에 대하여 미분하면 ​

나. y = xr 의 미분법 (단, r은 유리수)

몫의 미분법을 사용하여 n이 정수인 범위에서 (xn)' = nxn-1 이 성립한다는 것을 알았다.

이제 음함수의 미분법을 이용하면 n이 유리수인 범위에서도 성립한다는 것을 알 수 있다.

y = xr (r은 유리수)을 미분해 보자

임의의 유리수 r에 대하여 r = n/m (m,n은 정수, m≠0)으로 나타낼 수 있다.​

이 식의 양변을 x에 대하여 미분하면 음함수의 비분법에 의하여​

【 y = x^r 의 도함수 (단, r는 유리수】​

[예제]​​

5. 역함수의 미분법

미분가능한 함수 y = f(x)의 역함수 y = f-1 (x)가 존재하고 미분가능할 때 f-1(x)의 도함수를 구해보자.

역함수의 관계에 의해 f(a) = b 이면 f-1(b) = a 이므로 함수 y = f-1 (x)의 x = b 에서의 미분계수를 구한 다음,

이것이 y = f(x)의 x=a 에서의 미분계수와 어떤 관계가 있는지 살펴 보자.

도함수의 정의에 의해 함수 y = f-1(x) 의 x = b에서의 미분계수는​

아래 그림과 같이 f-1(b)=a이고 f-1(b+h)=a+h' 이라고 하면 h' → 0 이므로

이를 미분의 정의에 의해 미분을 하면​

이것을 정리하면 다음과 같이 표현할 수 있다.​

이제 좀 더 범위를 확장하여 앞에서 배운 음함수의 미분을 이용하여 함수와 그 역함수의

도함수 사이의 관계를 확인해 보자.

y = f-1 (x) 라 하면 x = f(y)이고 양변을 x에 대하여 미분하면 좌변과 우변은 각각​

한편, x = f(y) 에서 양변을 y에 대하여 미분하면 dx/dy = f'(y) 이므로 다음이 성립한다.​

따라서 역함수의 미분법을 이용하면 역함수를 직접 구하지 않고도 역함수의 도함수를 구할 수 있다.

【 역함수의 미분법 】​

[예제] 함수 f(x)=x2 (x≥0) 의 역함수를 y=f-1 (x)라 하자. 역함수의 미분법을 이용하여

(f-1)'(4)의 값을 구하여라.

<풀이> f-1 (4) = a 라 하면 f(a) = 4 이므로 a2=4 a=2 ∵ a ≥ 0

역함수의 미분법에 의해​

[참고]​

가. 우리가 다루는 대부분의 함수는 일차함수 y = ax+b, 이차함수 y=ax2+bx+c, 지수함수 y= ax, 로그함수 y= log ax,

      삼각함수 y = sin x 등의 함수가 모두 양함수로 표현되어 있어야 한다고 생각하기 쉽다. 예를 들어 함수의 표현에

      있어서 y5 =2x+1 보다는 y=(2x+1)1/5 이라는 형태에 익숙하고 편안함을 느낀다. 하지만 모든 함수가 항상 양함수

      로 표현이 가능한 것은 아니며, 양함수로 표현한다고 하더라도 복잡한 형태를 띠게 되는 경우가 많으므로

      dy/dx = 1/dx/dy는 이런 상황에서 큰 역할을 한다.

      예를 들어 음함수 y3+y2=3x+2를 y=f(x)로 바꾼 다음에 도함수 dy/dx= f'(x)를 구하는 것은 쉽지 않다.

      하지만 양변을 y에 대하여 미분을 하면​

나. 기호 dy/dx 는 독일의 수학자 라이프니츠가 처음 사용한 기호로서 dy를 dx로 나눈 분수가 아니라 그대로 하나의 도함수

      를 나타낸다. 하지만 합성함수나 역함수의 미분법에서는 dy/dx를 형식적으로 분수와 같이 다룰수 있는데,

      이는 라이프니츠 미분법의 장점이라고 할 수 있다.

      앞에서 배운 매개변수로 표현된 함수의 미분법에서도​

#몫의미분법 #몫 #도함수 #미분법 #합성함수 #겉미분 #속미분 #매개변수 #함수

#음함수 #양함수 #역함수 #라이프니츠 #로그함수 #삼각함수 #지수함수 #분수

#일차함수 #이차함수

미분의 개념을 이야기할 때 미분계수는 어떤 함수의 특정점에서 접선의 기울기값이라고 했다.

특정 점에서 접선의 기울기를 구하기 위하여 극한값을 구하는 과정도 알아 보았다.

그런데 함수 y = f(x)에 대하여 f'(1), f'(2), f'(3) … f'(100)을 구한다면 미분계수의 정의

를 이용하여 미분값을 구한다면 평균변화율의 극한값을 100번을 계산하여야 하는데 이는

번거롭고 효율적이지 못하다. 이런 경우에 x에서의 f'(x)를 함수값으로 하는 새로운 함수

y = f'(x)를 구하여 x값을 대입하면 보다 효율적으로 미분값을 계산할 수 있다.

이와 같이 어떤 함수 y = f(x) 함수에서 x값에 있어서의 미분값으로 하는 새로운 함수

y = f' (x)를 y = f(x)의 도함수라고 한다.

​

1. 도함수의 뜻

​

가. 도함수의 정의

함수 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는​

따라서 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는 a의 값을 2배하여 구할 수 있다. 즉,

f'(1) = 2, f'(√2) =2 √2, f'(π) = 2π, … f'(x) = 2x 이다.

일반적으로 함수 y = f(x)가 정의역 X에서 미분가능하면 정의역에 속하는 모든 x에 대하여

미분계수 f'(x)를 대응시키는 새로운 함수​

이를 그림으로 나타내면 다음과 같다.

이 때, 함수 f'(x)를 f(x)의 도함수라고 하고, 이것을 기호로

함수 y = f(x) 에서 그 도함수 f'(x)를 구하는 것을 함수 y = f(x)를 x에 대하여 미분한다고 하고 그 계산법을 미분법이라고

한다.​

【평균변화율, 미분계수, 도함수의 비교】

함수 y = f(x) 에서​

   ① 구간에서 x의 증분과 y의 증분의 비율

   ② 기하학적 의미 : 두 점 P(a, f(a), Q (b, f(b))를 지나는 직선의 기울기​

   ① 특정한 값 x = a 에서 평균변화율의 극한

   ② 기하학적 의미 : 곡선 y = f(x) 위의 점 P(a, f(a) 에서의 접선의 기울기​

   ① 특정값이 아닌 정의역에 속하는 임의의 x에 대한 미분계수 함수

   ② 기하학적 의미 : 곡선 y = f(x) 위의 임의의 점 (x, f(x))에서의 접선의 기울기

​

2. 미분법의 공식

도함수의 정의에서 도함수가 존재한다면 주어진 함수의 도함수를 구할 수 있게 된다.

그런데 도함수를 구할 때 정의에 의한 극한의 식으로 도함수를 구하기는 번거롭게 복잡

하다. 따라서 도함수를 구할 때 정의에 의해서 구하는 것보다 공식으로 도함수를 구하면

쉽고 편리하게 구할 수 있다.

​

가. 도함수의 정의에 이용하여 함수 f(x) = xn (n은 양의 정수)의 도함수를 구해 보자.​

인수분해 하면​

나. 상수함수 f(x) = C (C는 상수)의 도함수는

상수함수는 모든 점에서의 접선의 기울기가 항상 0이라는 것을 알 수 있다.

한편 아래의 미분법의 공식과 함수 y = xn 의 미분법을 이용하면 도함수의 정의를 이용하지

않더라도 다항함수​

의 도함수를 구할 수 있다.

【미분법의 도함수】

 두 함수 f(x), g(x)의 도함수가 존재할 때

   ① y = cf(x) 이면 y' = c f'(x) (단, c 는 상수)

   ② y = f(x) ± g(x) 이면 y' = f'(x) ± g'(x) (복부호 동순)

   ③ y = f(x) g(x) 이면 y' = f'(x) g(x) + f(x) g'(x) 가 된다.

또한 세함수 f(x), g(x), h(x)가 미분가능하면 함수 y = f(x) g(x) h(x) 도 미분가능하고

y' =f'(x) g(x) h(x)+ f(x) g'(x) h(x)+ f(x) g(x) h'(x) 이다.

​

다. 구간별로 정의된 함수의 도함수

구간별로 정의된 함수

f(x)= x (x < 0), x3 (x≥0) 의 도함수를 구할 때

각 구간의 도함수를 구하여 다음과 같이 나타내는 잘못을 해서는 안된다.

f'(x) = 1 (x <0), 3x2 (x ≥0)

구간의 경계가 되는 x = 0에서 평균변화율의 우극한은 0, 좌극한은 1로 같지 않기 때문에

x = 0 에서의 미분계수는 존재하지 않게 된다.

따라서 아래와 같이 나타내야 한다.

f'(x) = 1 (x <0), 3x2 (x >0)

일반적으로 구간별로 정의된 함수가 주어졌을 때, 그 구간의 경계점에서의 미분가능성은 알

수 없다. 경계점에서 미분가능하려면 미분계수가 존재해야 한다. 즉, 경계점에서의 평균변

화율의 극한이 존재해야 하므로 반드시 우극한과 좌극한이 서로 같은지 확인해야 한다.

참고로​

x = a 를 기준으로 나눠서 정의된 다항함수에서의 기하학적인 의미의 y = f(x)의 그래프가

x = a 에서 이어져 있고, 우극한에서의 접선의 기울기와 좌극한에서의 접선의 기울기가

같아야 한다.

​

#도함수 #비분 #우극한 #좌극한 #기하학 #다항함수 #기울기 #미분계수 #함수 #경계점

#평균변화율 #극한 #접선 #정의역 #방정식 #상수 #상수함수