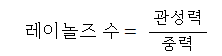열역학은 에너지를 다루는 과학으로 정의된다. 모든 사람이 에너지가 무엇인지에 대한 느낌을 가지고 있지만 에너지에 대한 엄밀한 정의를 하는 것은 쉽지 않다. 에너지는 변화를 일으키는 능력이라고 볼 수 있다. 열역학은 그리스어의 therme (heat)와 dynamics (power)로 부터 유래된 것으로 열을 동력으로 변환시키고자 한 초창기의 노력을 가장 적절하게 표현한 말이다. 오늘날 열역학은 동력 방생, 냉동 그리고 물질의 상태량 사이의 관계 등을 포함한 모든 형태의 에너지와 에너지 변환을 포함하는 것으로 광범위하게 이해되고 있다.
가. 에너지 보존법칙 (conservation of energy principle)
에너지 보존법칙은 가장 기초적인 자연법칙중의 하나이다. 이 법칙은 상호작용 중에 에너지는 한 형태에서 다른 한 형태로 변화할 수 있으나 에너지의 총량은 일정하다는 것을 의미한다. 즉, 에너지는 생성되거나 소멸될 수 없다는 의미이다. 예를 들면 절벽에서 떨어지는 바위는 위치에너지가 운동에너지로 변환되기 때문에 속도가 증가한다. 또한 에너지 보존 법칙은 다이어트 산업의 근간이 된다. 운동에 의하여 나가는 에너지 보다 음식물을 통해 들어 오는 에너지가 많은 사람은 체중이 증가하고 지방형태로 에너지가 저장되며 나가는 에너지 보다 들어오는 에너지가 적은 사람은 체중이 감소한다. 인체나 그 밖의 계에서 에너지의 변환은 들어 오는 에너지와 나가는 에너지의 차이와 같으며 에너지의 평형은 다음과 같이 표현된다.
E in - E out = △ E
나. 열역학 제1법칙 (first law of thermodynamics)
열역학 제1법칙은 단순히 에너지 보존법칙에 대한 표현이며 에너지가 열역학적 상태량이라는 의미를 내포하고 있다.
다. 열역학 제2법칙 (second law of thermodynamics)
열역학 제2법칙은 에너지가 양 (quantity) 뿐만 아니라 질 (quality)을 저하시키는 방향으로 진행된다는 것을 의미한다. 예를 들어 책상 위에 있는 뜨거운 커피잔은 결국 차가워지지만, 반대로 차가운 커피잔은 저절로 뜨거워지지는 않는다. 커피잔의 열은 주위의 공기로 에너지가 전달되고 나면 커피의 고온에너지는 질이 저하된다. 낮은 온도에 있는 덜 유용한 형태로 변환된다. 열역학 법칙 들은 우주가 창조된 이래로 존재해 왔지만 영국에서 1697년에 Thomas Savery에 의해, 그리고 1712년 Thomas Newcomen에 의해 최초의 성공적인 대기 증기기관 (atmospheric system engine)이 만들어 지기 전까지 열역학은 과학으로 출현하지 못했다. 이 기관들은 매우 느리고 비효율적이었지만 새로운 과학발전에 대한 길을 열었다.
열역학 제1법칙과 제2법칙은 1850년에 William Rankine, Rudolph Thompson 의 연구결과로 부터 동시에 출현하였다. 열역학 (Thermodynamics)이라는 용어는 1849년 Lord Kelvin 의 저서에서 처음 사용되었고, 최초의 열역학 교과서는 Glasgow 대학의 교수인 William Rankine에 의해 1859년에 저술되었다. 물질이 분자라고 하는 수많은 입자로 구성되어 있다는 것은 잘 알려진 사실이다. 물질의 상태량은 이들 입자의 거동에 따라 달라진다. 예를 들어 용기내에 들어 있는 기체의 압력은 분자들과 용기벽 사이의 운동량 전달의 결과이다. 그러나 용기내의 압력을 결정하기 위해 기체입자의 거동을 알아 낼 필요는 없다. 용기내에 압력계를 부착하는 것으로 충분하다. 열역학 연구에 있어서 각각의 입자거동에 대한 부석이 필요없는 거시적 접근법을 고전열역학 (classical thermodynamics)이라고 한다. 고전열역학은 공학문제 해결에 대한 직접적이면서도 쉬운방법을 제공한다. 많은 입자 집단의 평균거동에 대한 미시적 접근방법은 통계 열역학 (statistical thermo-dynamics)이라고 한다.
라. 열역학의 응용분야
자연계의 모든 활동은 에너지와 물질 사이의 상호작용을 수반한다. 따라서, 이러한 관점에서 볼 때 어떤 방식으로든 열역학과 관계되지 않은 분야가 없다고 할 수 있다. 열역학에 관련된 문제는 여러 공학분야나 우리 일상 생활에서 흔히 접할 수 있으므로 응용분야를 너무 멀리서 찾을 필요가 없다. 심장은 인체의 모든 부분에 계속하여 혈액을 보내고 수조개의 달하는 인체의 세포에서는 여러 형태의 에너지 변환이 이루어지며 발생된 인체 내의 열은 대기중으로 방출된다. 인체가 느끼는 안락함은 이와같은 신진대사로 부터 발생된 열의 방출과 밀접하게 관련되어 있다. 따라서, 사람들은 환경조건에 따라 의복을 바꾸어 주위로의 열전달률을 조절한다. 그밖의 다른 열역학의 응용분야도 우리가 거주하는 곳에서 쉽게 찾을 수 있다.
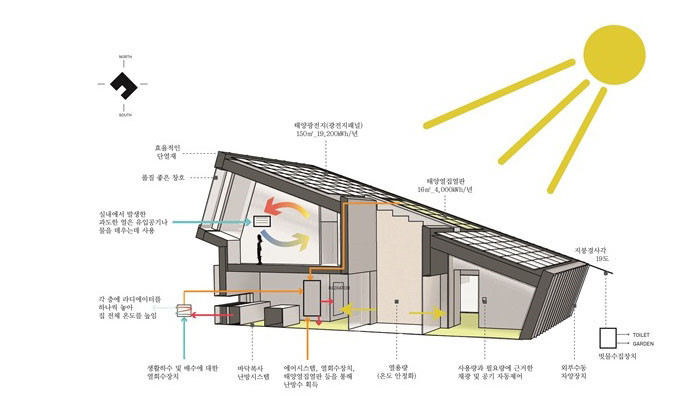
통상적인 집은 어떤 면에서 열역학의 경이로움으로 가득찬 전시관이다. 대부분의 가정용품과 설비들은 전체적으로 또는 부분적으로 열역학 원리를 이용하여 설계된다. 예를 들면 전자 레인지나 가스레인지, 냉난방 시스템, 냉동기, 가습기, 압력밥솥, 온수기, 샤워기, 다리미, 컴퓨터, TV 등이 있다. 보다 큰 규모로서 열역학은 자동차 엔진, 로케트, 제트엔진 그리고 재래식 및 원자력 발전소, 태양열 집열기 등의 설계와 해석, 그리고 일반적인 스용차로 부터 항공기에 이르는 수송수단들의 설계에 있어서도 중요한 부분을 담당한다. 예를 들면 에너지 효율적 주택은 겨울에는 열 손실이, 그리고 여름에는 가열이 최소가 되도록 설계된다. 컴퓨터에 설치된 휀의 크기, 위치 및 동력 등도 열역학을 포함하는 해석과정을 통하여 선정된다.
#열역학 #에너지보존법칙 #에너지 #위치에너지 #운동에너지 #상태량
'소방설비기사 (기계) > 소방유체역학' 카테고리의 다른 글
| 일과 열의 비교 관련 문제 풀이 (0) | 2023.09.15 |
|---|---|
| 엔탈피(enthalpy)와 에너지 방정식 (0) | 2023.09.12 |
| 부력 (浮力) 이란 ? (0) | 2023.09.06 |
| 펌프의 이상현상 (0) | 2023.09.06 |
| 배관의 주손실과 부차적 손실 (0) | 2023.09.05 |