아낌없이 주는 나무

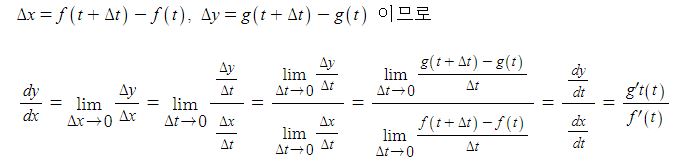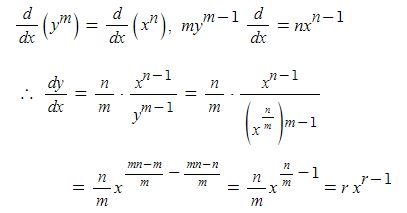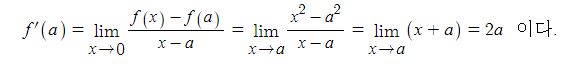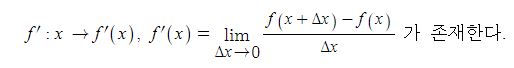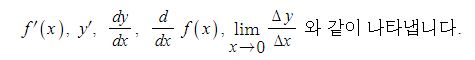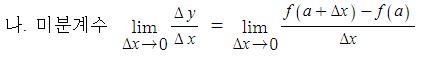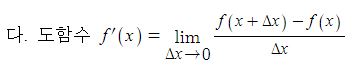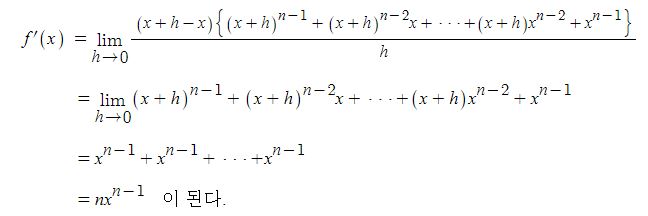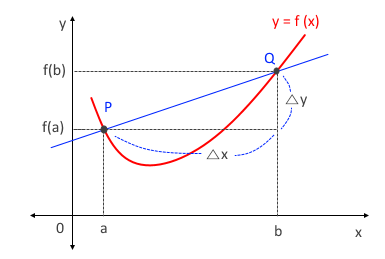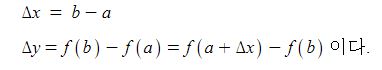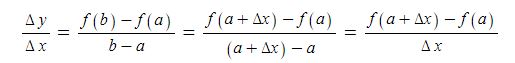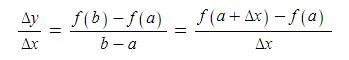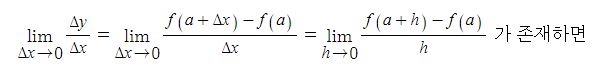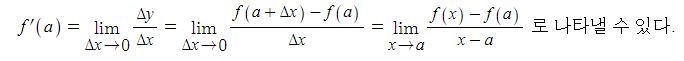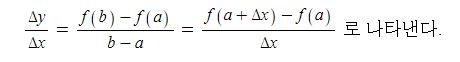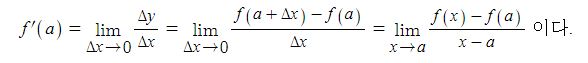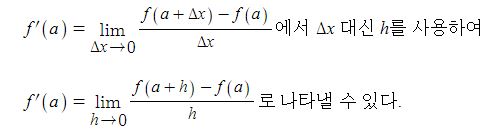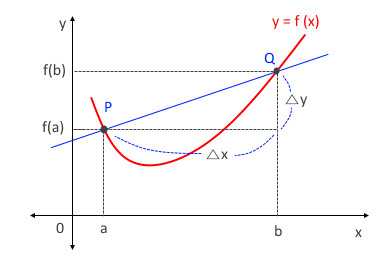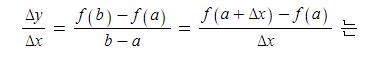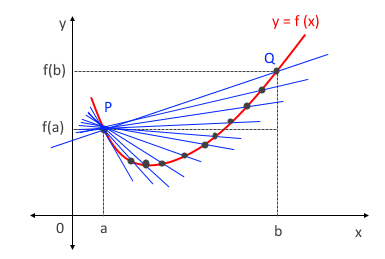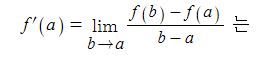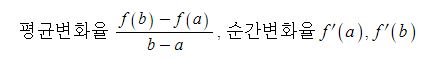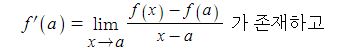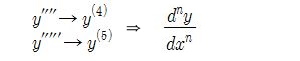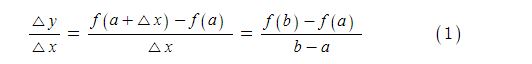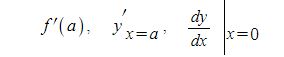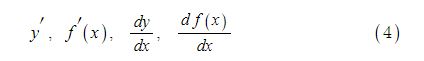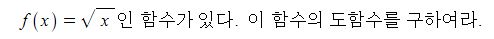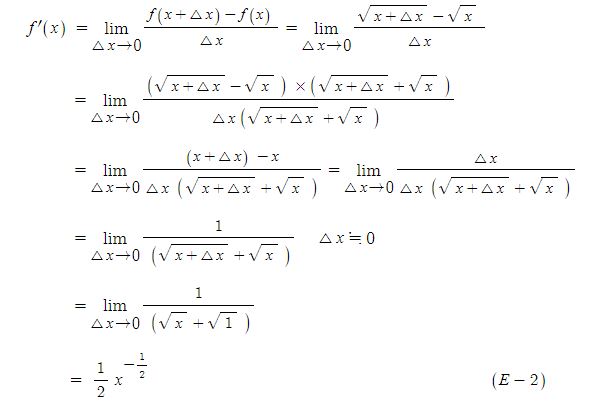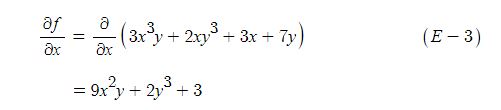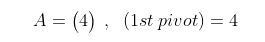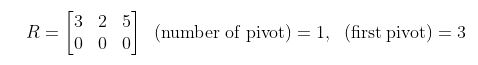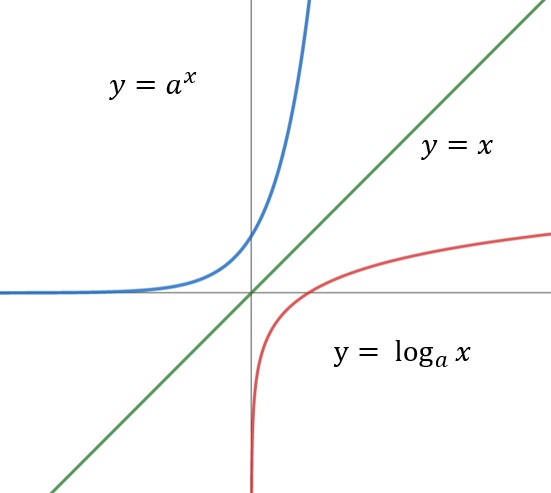
삼각함수의 덧셈 또는 뺄셈을 곱셈으로 고치는 공식과 삼각함수의 극한을 이용하여 삼각함수의 도함수를, 지수함수와

로그함수의 극한을 이용하여 지수함수와 로그함수의 도함수를 구하는 방법을 알아 보자. 또한 이계도함수의 정의와

이계도함수의 계산법도 알아 보자.

​

1. 삼각함수의 도함수

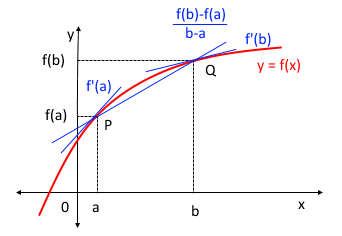
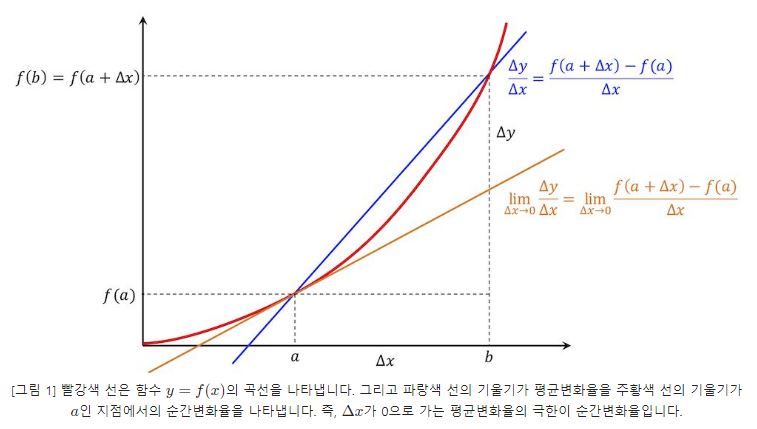
삼각함수의 도함수를 구하려면 임의의 점에서의 미분계수를 구하면 되는데 삼각함수의 극한을 구할 수 있다.​

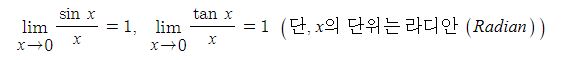
가. 삼각함수 y = sin x, y = cos x, y = tan x 의 도함수는 도함수의 정의와 삼각함수의 극한, 삼각함수의 합 또는 차를

      곱으로 변환하는 공식을 이용하여 구할 수 있다.

① y = sin x 의 도함수​

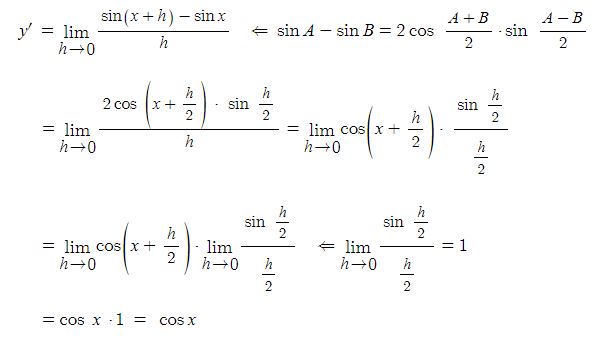
따라서 (sin x)' = cos x 이다.

​

② y = cos x의 도함수​

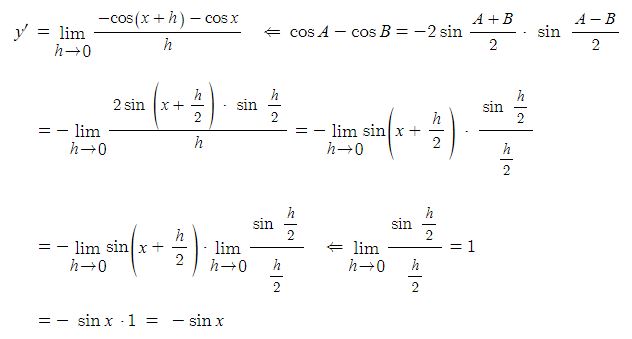
따라서 (cos x)' = - sin x 이다.

​

③ y = tan x 의 도함수​

   따라서 (tan x)' = sec2 x 이다.

​

나. 삼각함수 y=cosec x, y = sec x, y = cot x 의 도함수도 바로 위에서 구한 세 삼각함수의 도함수와 몫의 미분법을

      적용하여 구할 수 있다.

① y = cosec x 의 도함수​

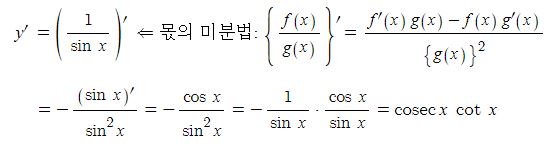
② y = sec x 의 도함수​

   따라서 (sec x)' = sec x · tan x 이다.

③ y = cot x 의 도함수  ​

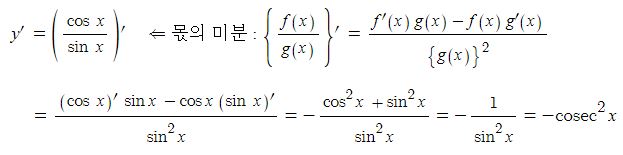
【 삼각함수의 도함수】​

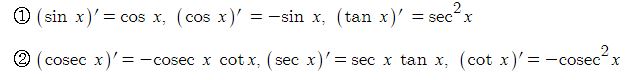
2. 지수함수의 도함수

지수함수 y = e^x, y = a^x 의 도함수는 도함수의 정의와 지수함수의 극한을 이용하여 구할 수 있다.​

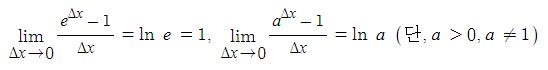
가. y = e^x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

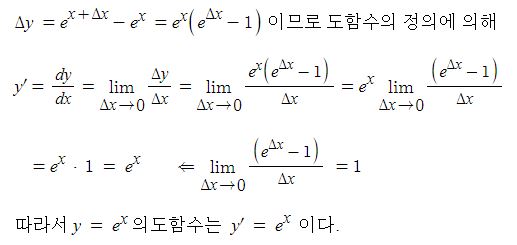
나. y = ax (a >0, a ≠ 1) 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 하면​

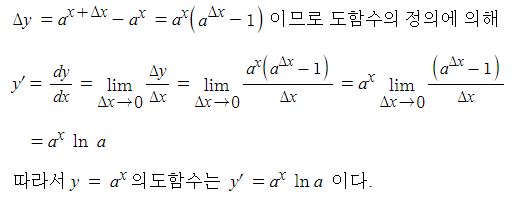
참고로 합성함수의 미분법을 이용하여 y = ex 의 도함수를 구할 수 있다.​

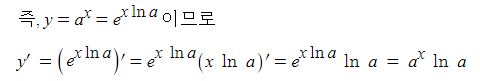
3. 로그함수의 도함수

로그함수 y = ln x, y = log ax (a >0, a ≠1)의 도함수는 도함수의 정의와 무리수 e의 정의에 의하여 구할 수 있다.​

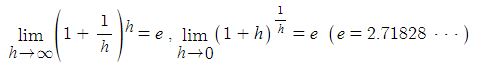
가. 로그함수의 도함수

y = ln x 의 도함수를 구해 보자.

x의 변화량을 △x, x에 대한 y의 변화량을 △y이라고 한다면

△y = ln (x+△x) - ln x 가 되므로 도함의 정의에 의해​

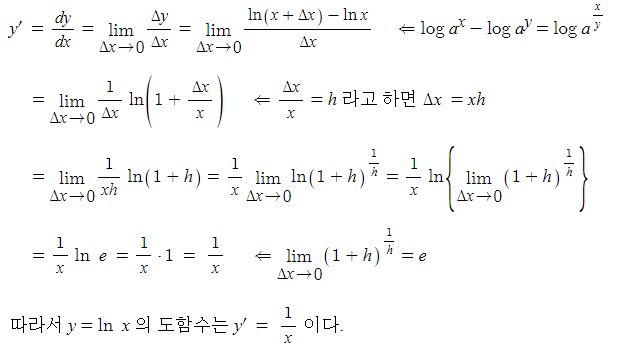
또한 로그의 성질 log ax = ln x / ln a (a >0, a≠1)를 이용하면 다음과 같이 y =log ax 의 도함수를 구할 수 있다.​

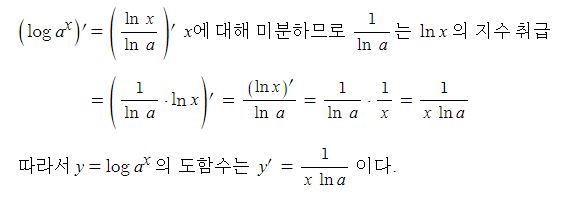
나. 절대값을 포함한 로그함수의 도함수

미분가능한 함수 f(x)에 대하여 f(x) > 0 또는 f(x) <0 인 경우에 ln lf(x)l 의 도함수를 구해 보자.

① f(x) > 0 일 때, lf(x)l = f(x)이므로 u = f (x)로 놓으면 y = ln u​

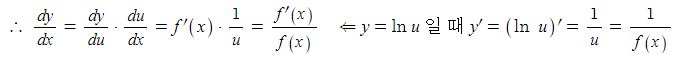
② f(x) < 0 일 때, lf(x)l = -f(x)이므로 u = -f (x)로 놓으면 y = ln u​​

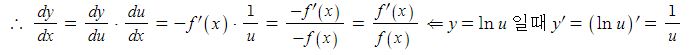
【 로그함수의 도함수 】​

따라서 ①, ② 를 정리하여 보면​

4. 로그 미분법

가. 로그 미분법

밑과 지수에 모두 변수를 포함하는 지수형태의 함수나 복잡한 분수함수의 도함수를 구하기 위해서는 양변에 로그를

취한 후 합성함수의 미분법이나 음함수의 미분법을 적용하면 된다.

이런 방법을 로그미분법이라고 한다. 이때 로그의 진수가 양수이어야 하므로 로그를 취하기 전에 식의 양변에 절대값을

먼저 취한 다음 로그를 택해야 한다. 만약 이미 양변이 양수일 때는 절대값을 취하지 않아도 된다.​

몫의 미분법과 합성함수의 미분법을 적용하면 도함수를 구할 수 있지만 식이 매우 복잡하므로 로그를 취한 후 음합수

미분법을 이용하여 도함수를 구하는 것이 보다 빠르고 쉽다.

양변이 모두 양수이므로 식의 양변에 자연로그를 취하여 로그의 성질을 이용한다.​

즉, 함수 y = f(x) 에서 f(x)의 형태가 일반적인 미분법을 적용하기에 복잡한 형태라면 로그미분법을 이용해서

다음 순서에 따라 함수의 도함수를 구할 수 있다.

【 로그 미분법 】

복잡한 지수와 몫으로 표현된 함수는 로그미분법을 이용하여 도함수를 구할 수 있다.

① 양변에 절대값을 취한다. ⇒ ㅣyㅣ= l f(x)ㅣ

② 양변에 자연로그를 취한다. ⇒ ln ㅣyㅣ = ln l f(x)ㅣ​

나. y = xa 의 도함수 (단, a는 실수)

자연수 지수에서 부터 유리수 지수까지는 함수 y = x'의 도함수가 y'=r xr-1 이다.

이제 로그미분법을 이용하여 a가 임의의 실수일 때, 함수 y = xa의 도함수를 구해 보자.​

【 로그 미분법의 활용 】

가. 지수함수 y = ax (a > 0, a ≠ 1)의 도함수를 로그미분법을 이용하여 구해 보자.

      y = ax 의 양변에 자연로그를 취하면 ln y = ln ax = x ln a

      양변을 x에 대하여 미분하면​

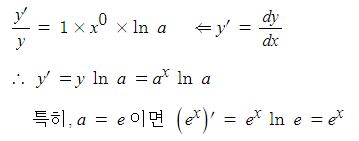
   위 식은 지수함수를 미분해서 얻은 도함수와 그 결과가 일치한다.

나. 이번에는 y =af(x) 의 도함수 (a>0, a≠1)를 로그미분법을 이용하여 구해 보자.​

   이 또한 지수함수를 포함한 합성함수의 도함수와 그 결과가 일치한다.

​

5. 이계함수

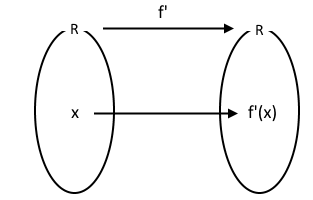
함수 y = f(x) 의 도함수 f'(x)가 미분가능하면 f'(x)의 도함수는 다음과 같다.​

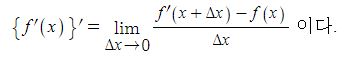
이 때, f'(x)의 도함수를 함수 f(x)의 이계 도함수라고 하고 기호로는 다음과 같이 나타낸다.​

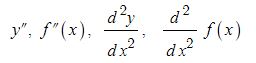
즉, 이 이계도함수는 어떤 함수를 두번 미분한 함수이다.

일반적으로 자연수 n 에 대하여 함수 y = f(x)가 n번 미분가능한 함수일 때 y = f(x)를 n번

미분하여 얻은 함수를 y = f(x)의 n계도함수라고 하고 기호로는 다음과 같다.​

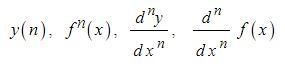
【 이계 도함수 】

함수 y = f(x)의 도함수 f'(x) 가 미분가능할 때, f'(x)의 도함수를 y = f(x)의 이계도함수라

하고 기호로는 다음과 같이 나타낸다.​

#삼각함수 #도함수 #미분 #미분계수 #지수함수 #합성함수 #극한 #미분법 #평균변화율

#로그함수 #절대값 #로그미분법 #이계도함수

두 함수를 몫으로 표현된 함수, 합성함수, 음함수, 역함수, 매개변수로 표현된 함수 등

다양한 형태의 함수의 미분법에 대하여 알아 보자.

​

1. 몫의 미분법

가. 몫의 미분법​

위 함수는 도함수의 정의를 이용하여 다음과 같이 풀이할 수 있다.​

위와 같이 매번 도함수의 정의를 이용하여 도함수를 구하는 것은 복잡하고 시간이 많이

걸리게 되는데 몫의 미분법은 결과를 공식화하여 기억하자.​

[예제] 몫의 미분법을 이용하여​

【 몫의 미분법 】

두 함수 f(x), g(x) (g(x) ≠ 0)가 미분가능할 때

이와 같이 몫의 미분은 결과 공식을 외워 두자.​

n이 자연수일 때 다항함수 y = xn 의 도함수가 y' =n xn-1 이다. 그런데 몫의 미분법을 이

용하면 n이 정수일 때도 위 사실이 성립함을 알 수가 있다.​

①,②,③에서 알 수 있듯이 n이 양수일 때 뿐만 아니라 0이거나 음의 정수일 때에도 함수

y = xn 의 도함수 y' = n xn-1 이 된다. 즉, 임의의 정수 n에 대하여 y = xn 의 도함수는

y' = n x n-1 이 된다.

​

【 y = xn 의 도함수 (단, n은 정수) 】​

2. 합성함수의 미분법

가. 합성함수의 미분법

함수 y = (2x -3)3 의 도함수를 구하려면 다음과 같이 식을 전개한 후 미분해야 한다.​

이 처럼 다항함수의 차수가 조금만 높아도 전개한 다음 미분하는 것은 여간 복잡한 것이 아니다.

따라서 함수를 전개하지 않고 미분할 수 있는 방법이 있다면 그 방법을 이용하는 것이 빠르고 계산과정도 간단하다.

합성함수의 도함수가 어떻게 나타나는지를 확인해 보면 그 방법을 구체적으로 확인할 수 있다.

두 함수 y = f(u), u = g(x) 가 미분 가능할 때, 도함수의 정의를 이용하여 합성함수

y =f (g(x))의 도함수를 구해 보자.​​

위 식에서 앞, 뒤 두 극한 값을 찾으면 함성합수의 도함수를 구할 수 있다.

① 앞 함수의 극한 값

g(x+h) = B, g(x) = A 라고 하면 함수 y = g(x)미분 가능하므로 연속이다.

따라서 h → 0 일 때, g(x+h) → g(x) 이므로 h → 0 이면 B → A 이다.​

② 뒤 함수의 극한값은 도함수의 정의에 의해 g'(x)가 된다.

따라서 ①, ② 에 의해 합성함수 y = f(g(x))의 도함수는 다음과 같다.​

[예제] 함성합수의 미분법을 이용하여 함수 y = (2x-3)3의 도함수를 구해 보자.

이 함수를 f(u)=u3 과 g(x) = 2x-3의 합성합수라고 하면​

[합성함수의 미분법]​

【 합성함수의 미분은 (겉미분) × (속미분)】

합성함수 y = f(g(x))의 도함수를 다음과 같이 기억하자.

① 바깥 쪽 함수 f(x)를 미분하고 안의 함수 g(x)는 그냥 둔 다음 ☜ 겉미분 f'(g(x))

② 안쪽 함수 g(x)를 미분하여 ☜ 속미분 g'(x)

③ 겉미분과 속미분을 곱한다. ☜ f'(g(x)) · g'(x)

위 사실을 적용해 보면​

3. 매개변수로 표현된 함수의 미분법

x = t - 1, y = t2 + 1 과 같이 변수 t에 대한 함수 x, y가 주어져 있을 때, 함수 x, y를 각각

t에 대한 한수로 볼 수 있지만 중복되는 변수 t를 소거하여 y를 x에 대한 하나의 함수로 볼

수도 있다. 즉, x = t-1 에서 t = x+1 이므로 이를 y = t2 + 1에 대입하여 변수 t를 소거하면​

따라서 y는 t에 대한 함수이기도 하지만 x에 대한 함수이기도 하다.

이와 같이 두 변수 x, y의 함수 관계가 변수 t를 매개로 하여 x = f(t), y = g(t)의 꼴로 표현

될 때, 변수 t를 매개변수라 하고 x = f(t), y = g(t)를 매개변수로 표현된 함수라고 한다.

매개변수로 표현된 함수 x = f(t), y = g(t)의 도함수를 구하기 위해서는 매개변수 t를 소거

하여 y = f(x) 꼴의 함수로 고친 다음 미분해야 한다.​

함수 x = f(t), y = g(t)가 t에 대하여 미분가능하고 f(t) ≠ 0이면 x=f(t)의 역함수가 존재하고 t는 x의 함수이므로

y = g(t)도 x의 함수로 볼 수 있다.

따라서 t의 증분 △t에 대한 x의 증분을 △x. y의 증분을 △y라 하면 △x→0 일 때 △t→0 이고,​​

【 매개 변수로 표현된 함수의 미분법】

x = f(t), y = g(t) 가 t에 대하여 미분가능하고 f'(t) ≠ 0 이면​

예제 : 매개변수로 표현된 함수의 미분법​

4. 음함수의 미분법

가. 음함수의 미분법

일반적으로 함수는 정의역의 원소 x와 공역의 원소 y 사이의 관계식으로 표현할 수 있다.​

왼쪽과 같이 y = f(x)의 꼴일 때 y를 x의 양함수(Explicit function)라고 하고, 오른쪽과 같이 f(x,y) = 0 의 꼴일 때

y를 x의 음함수 (Implicit function)라고 한다.

음함수 f(x,y) = 0 을 양함수 y = f(x)의 꼴로 고칠 수 있다면 양함수로 변형한 다음 미분하여 도함수를 구할 수 있다.

하지만 음함수 x3+y2+2y+3 = 0 처럼 양함수로 고치기가 어려운 함수들에 대하여 음함수를 양함수 y = f(x)의 꼴로

고치지 않고 바로 미분할 수 있는데 이를 음함수의 미분법이라고 한다.

양함수든 음함수든 미분계수와 도함수는 모두 정의역의 원소인 x의 변화량에 따른 함수값 y의 변화량의 극한을 뜻하는

것이고 이것을 dy/dx라는 기호를 써서 나타낸다. 음함수는 비록 f(x,y) = 0 의 형태를 띠고 있다고는 하지만 y가 x에 대한

함수라고 가정을 한다.

따라서 문자 y를 포함하고 있는 항을 x에 대하여 미분할 때에는 y를 x의 함수로 보고 합성함수의 미분법을 적용하여

미분하는 것이 음함수의 미분법의 핵심이다.

음함수 x2 + y2 = 1 에 위의 사실을 적용해서 양변을 x에 대하여 미분하면​

[예제] 음함수의 미분법을 이용하여 x3+y2+2y+3=0 의 도함수를 구해 보자.

양변을 x에 대하여 미분하면​

【음함수의 미분법】

x의 함수 y가 음함수 f(x, y) = 0 의 꼴로 주어졌을 때, y를 x의 함수로 보고 각 항을 x에 대하여 미분하여 dy/dx를 구한다.

예제 : 음함수의 미분법을 이용하여 xy = 4 의 도함수 dy/dx를 구하여라.

[풀이] y를 x의 함수로 보고 각 항을 x에 대하여 미분하면 ​

나. y = xr 의 미분법 (단, r은 유리수)

몫의 미분법을 사용하여 n이 정수인 범위에서 (xn)' = nxn-1 이 성립한다는 것을 알았다.

이제 음함수의 미분법을 이용하면 n이 유리수인 범위에서도 성립한다는 것을 알 수 있다.

y = xr (r은 유리수)을 미분해 보자

임의의 유리수 r에 대하여 r = n/m (m,n은 정수, m≠0)으로 나타낼 수 있다.​

이 식의 양변을 x에 대하여 미분하면 음함수의 비분법에 의하여​

【 y = x^r 의 도함수 (단, r는 유리수】​

[예제]​​

5. 역함수의 미분법

미분가능한 함수 y = f(x)의 역함수 y = f-1 (x)가 존재하고 미분가능할 때 f-1(x)의 도함수를 구해보자.

역함수의 관계에 의해 f(a) = b 이면 f-1(b) = a 이므로 함수 y = f-1 (x)의 x = b 에서의 미분계수를 구한 다음,

이것이 y = f(x)의 x=a 에서의 미분계수와 어떤 관계가 있는지 살펴 보자.

도함수의 정의에 의해 함수 y = f-1(x) 의 x = b에서의 미분계수는​

아래 그림과 같이 f-1(b)=a이고 f-1(b+h)=a+h' 이라고 하면 h' → 0 이므로

이를 미분의 정의에 의해 미분을 하면​

이것을 정리하면 다음과 같이 표현할 수 있다.​

이제 좀 더 범위를 확장하여 앞에서 배운 음함수의 미분을 이용하여 함수와 그 역함수의

도함수 사이의 관계를 확인해 보자.

y = f-1 (x) 라 하면 x = f(y)이고 양변을 x에 대하여 미분하면 좌변과 우변은 각각​

한편, x = f(y) 에서 양변을 y에 대하여 미분하면 dx/dy = f'(y) 이므로 다음이 성립한다.​

따라서 역함수의 미분법을 이용하면 역함수를 직접 구하지 않고도 역함수의 도함수를 구할 수 있다.

【 역함수의 미분법 】​

[예제] 함수 f(x)=x2 (x≥0) 의 역함수를 y=f-1 (x)라 하자. 역함수의 미분법을 이용하여

(f-1)'(4)의 값을 구하여라.

<풀이> f-1 (4) = a 라 하면 f(a) = 4 이므로 a2=4 a=2 ∵ a ≥ 0

역함수의 미분법에 의해​

[참고]​

가. 우리가 다루는 대부분의 함수는 일차함수 y = ax+b, 이차함수 y=ax2+bx+c, 지수함수 y= ax, 로그함수 y= log ax,

      삼각함수 y = sin x 등의 함수가 모두 양함수로 표현되어 있어야 한다고 생각하기 쉽다. 예를 들어 함수의 표현에

      있어서 y5 =2x+1 보다는 y=(2x+1)1/5 이라는 형태에 익숙하고 편안함을 느낀다. 하지만 모든 함수가 항상 양함수

      로 표현이 가능한 것은 아니며, 양함수로 표현한다고 하더라도 복잡한 형태를 띠게 되는 경우가 많으므로

      dy/dx = 1/dx/dy는 이런 상황에서 큰 역할을 한다.

      예를 들어 음함수 y3+y2=3x+2를 y=f(x)로 바꾼 다음에 도함수 dy/dx= f'(x)를 구하는 것은 쉽지 않다.

      하지만 양변을 y에 대하여 미분을 하면​

나. 기호 dy/dx 는 독일의 수학자 라이프니츠가 처음 사용한 기호로서 dy를 dx로 나눈 분수가 아니라 그대로 하나의 도함수

      를 나타낸다. 하지만 합성함수나 역함수의 미분법에서는 dy/dx를 형식적으로 분수와 같이 다룰수 있는데,

      이는 라이프니츠 미분법의 장점이라고 할 수 있다.

      앞에서 배운 매개변수로 표현된 함수의 미분법에서도​

#몫의미분법 #몫 #도함수 #미분법 #합성함수 #겉미분 #속미분 #매개변수 #함수

#음함수 #양함수 #역함수 #라이프니츠 #로그함수 #삼각함수 #지수함수 #분수

#일차함수 #이차함수

미분의 개념을 이야기할 때 미분계수는 어떤 함수의 특정점에서 접선의 기울기값이라고 했다.

특정 점에서 접선의 기울기를 구하기 위하여 극한값을 구하는 과정도 알아 보았다.

그런데 함수 y = f(x)에 대하여 f'(1), f'(2), f'(3) … f'(100)을 구한다면 미분계수의 정의

를 이용하여 미분값을 구한다면 평균변화율의 극한값을 100번을 계산하여야 하는데 이는

번거롭고 효율적이지 못하다. 이런 경우에 x에서의 f'(x)를 함수값으로 하는 새로운 함수

y = f'(x)를 구하여 x값을 대입하면 보다 효율적으로 미분값을 계산할 수 있다.

이와 같이 어떤 함수 y = f(x) 함수에서 x값에 있어서의 미분값으로 하는 새로운 함수

y = f' (x)를 y = f(x)의 도함수라고 한다.

​

1. 도함수의 뜻

​

가. 도함수의 정의

함수 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는​

따라서 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는 a의 값을 2배하여 구할 수 있다. 즉,

f'(1) = 2, f'(√2) =2 √2, f'(π) = 2π, … f'(x) = 2x 이다.

일반적으로 함수 y = f(x)가 정의역 X에서 미분가능하면 정의역에 속하는 모든 x에 대하여

미분계수 f'(x)를 대응시키는 새로운 함수​

이를 그림으로 나타내면 다음과 같다.

이 때, 함수 f'(x)를 f(x)의 도함수라고 하고, 이것을 기호로

함수 y = f(x) 에서 그 도함수 f'(x)를 구하는 것을 함수 y = f(x)를 x에 대하여 미분한다고 하고 그 계산법을 미분법이라고

한다.​

【평균변화율, 미분계수, 도함수의 비교】

함수 y = f(x) 에서​

   ① 구간에서 x의 증분과 y의 증분의 비율

   ② 기하학적 의미 : 두 점 P(a, f(a), Q (b, f(b))를 지나는 직선의 기울기​

   ① 특정한 값 x = a 에서 평균변화율의 극한

   ② 기하학적 의미 : 곡선 y = f(x) 위의 점 P(a, f(a) 에서의 접선의 기울기​

   ① 특정값이 아닌 정의역에 속하는 임의의 x에 대한 미분계수 함수

   ② 기하학적 의미 : 곡선 y = f(x) 위의 임의의 점 (x, f(x))에서의 접선의 기울기

​

2. 미분법의 공식

도함수의 정의에서 도함수가 존재한다면 주어진 함수의 도함수를 구할 수 있게 된다.

그런데 도함수를 구할 때 정의에 의한 극한의 식으로 도함수를 구하기는 번거롭게 복잡

하다. 따라서 도함수를 구할 때 정의에 의해서 구하는 것보다 공식으로 도함수를 구하면

쉽고 편리하게 구할 수 있다.

​

가. 도함수의 정의에 이용하여 함수 f(x) = xn (n은 양의 정수)의 도함수를 구해 보자.​

인수분해 하면​

나. 상수함수 f(x) = C (C는 상수)의 도함수는

상수함수는 모든 점에서의 접선의 기울기가 항상 0이라는 것을 알 수 있다.

한편 아래의 미분법의 공식과 함수 y = xn 의 미분법을 이용하면 도함수의 정의를 이용하지

않더라도 다항함수​

의 도함수를 구할 수 있다.

【미분법의 도함수】

 두 함수 f(x), g(x)의 도함수가 존재할 때

   ① y = cf(x) 이면 y' = c f'(x) (단, c 는 상수)

   ② y = f(x) ± g(x) 이면 y' = f'(x) ± g'(x) (복부호 동순)

   ③ y = f(x) g(x) 이면 y' = f'(x) g(x) + f(x) g'(x) 가 된다.

또한 세함수 f(x), g(x), h(x)가 미분가능하면 함수 y = f(x) g(x) h(x) 도 미분가능하고

y' =f'(x) g(x) h(x)+ f(x) g'(x) h(x)+ f(x) g(x) h'(x) 이다.

​

다. 구간별로 정의된 함수의 도함수

구간별로 정의된 함수

f(x)= x (x < 0), x3 (x≥0) 의 도함수를 구할 때

각 구간의 도함수를 구하여 다음과 같이 나타내는 잘못을 해서는 안된다.

f'(x) = 1 (x <0), 3x2 (x ≥0)

구간의 경계가 되는 x = 0에서 평균변화율의 우극한은 0, 좌극한은 1로 같지 않기 때문에

x = 0 에서의 미분계수는 존재하지 않게 된다.

따라서 아래와 같이 나타내야 한다.

f'(x) = 1 (x <0), 3x2 (x >0)

일반적으로 구간별로 정의된 함수가 주어졌을 때, 그 구간의 경계점에서의 미분가능성은 알

수 없다. 경계점에서 미분가능하려면 미분계수가 존재해야 한다. 즉, 경계점에서의 평균변

화율의 극한이 존재해야 하므로 반드시 우극한과 좌극한이 서로 같은지 확인해야 한다.

참고로​

x = a 를 기준으로 나눠서 정의된 다항함수에서의 기하학적인 의미의 y = f(x)의 그래프가

x = a 에서 이어져 있고, 우극한에서의 접선의 기울기와 좌극한에서의 접선의 기울기가

같아야 한다.

​

#도함수 #비분 #우극한 #좌극한 #기하학 #다항함수 #기울기 #미분계수 #함수 #경계점

#평균변화율 #극한 #접선 #정의역 #방정식 #상수 #상수함수

또한 x의 증분에 대한 y의 증분의 비율​

위 식을 x값이 a에서 b로 변할 때의 함수 y=f(x)의 평균변화율이라고 한다.

함수 y=f(x)의 평균변화율은 두점 P(a, f(a)), Q (b,f(b))을 지나는 직선의 기울기와 같다.​

나. 미분계수 (순간변화율)

함수 y=f(x)에서 x의 값이 a 에서 a+△x (=b)까지 변할 때, 평균변화율은 다음과 같다.​

여기서 △x → 0 일 때 평균변화율의 극한값이​

함수 y=f(x)는 x=a에서 미분가능하다고 하고 이 극한값을 함수 y=f(x)의 x=a에서의 순간변화율 또는 미분계수라고 하며

기호로는 f'(a)와 같이 나타내고 f prime a라고 한다. 또한 함수가 어떤 구간에 속하는 모든 x의 값에서 미분가능할 때,

함수 y=f(x)는 그 구간에 서 미분가능하다고 한다. 특히 함수 y=f(x)가 정의역에 속하는 모든 x 의 값에서 미분가능할 때

함수 y=f(x)는 미분가능한 함수라고 한다. 한편, a+△x=x라고 하면 △x=x-a이고 △x →0일 때 x→a 이므로​

다음 함수는 미분이 가능할까 ?​

함수 f(x)=x2 은 x=2에서 미분가능하고 그 때의 미분계수는 f'(2)= 4 이다.

​

[정리하면]

함수 y = f(x)에 대하여

① x의 값이 a에서 b까지 변할 때의 평균변화율은​

② x = a 에서의 미분계수(순간변화율)은​

또한 미분계수(순간변화율)은 다음과 같이 나타낼 수도 있다.​

다. 미분계수의 기하학적 의미

앞에서 x의 값이 a 에서 b까지 변할 때 함수 y=f(x)의 평균변화율​

따라서 함수 y=f(x)의 x = a 에서의 미분계수

곡선 y=f(x) 위의 점 P(a,f(a))에서의 접선 ℓ의 기울기와 같음을 알 수 있다.

[미분계수 f'(a)의 기하학적 의미

함수 y=f(x)에 대하여 x=a에서의 미분계수 f'(a)는 곡선 y=f(x) 위의 점 (a, f(a)에서의 접선의 기울기와 같다.

점 (a, f(a))에서의 접선이 x축의 양방향과 이루는 각을 θ 라 하면, 미분계수 f'(a)는 다음과 같다. f'(a) = tan θ

​

[평균변화율과 미분계수의 대소 관계]

평균변화율과 미분계수의 기하학적 의미를 이용하면 그 대소 관계를 알 수 있다.

함수 y=f(x)의 그래프가 위 그림과 같을 때, 다음 식의 값의 대소를 비교하여 보자.

다음 함수 y=f(x)의 그래프가 다음 그림과 같을 때

다음 식의 값의 크기를 비교해 보자.​

위 그래프는 아래로 볼록한 그래프로 위 식의 크기는 다음과 같다.​

2. 미분가능과 연속

앞에서 미분계수의 기하학적 의미는 곡선의 접선의 기울기와 같다고 했다. 그런데 불연속점

에서는 접선을 그릴 수 없으므로 미분이 가능하지 않다는 것을 예상할 수 있다.

그러면 연속인 점에서는 항상 접선을 그릴 수 있어 미분도 가능할까 ? 이에 대한 생각을 하

면서 y = f(x)의 연속과 미분가능 사이에는 어떤 관계가 있는지 알아 보자.

​

가. 미분가능 : 연속

함수 y = f(x)가 x = a에서 미분가능하면 함수 y=f(x)는 x=a에서 연속이다.

[증명]

함수 f(x)가 x = a 에서 미분가능하면 미분계수​

f'(a)는 일정한 값이므로 다음이 성립한다.​

따라서​

나. 연속 ≠ 미분가능

앞의 명제의 역 '함수 y = f(x)가 x = a 에서 연속이면 y = f(x)는 x = a 에서 미분가능하다'

는 거짓이다. 즉, 함수 y = f(x)가 x = a 에서 연속이지만 y = f(x)는 x = a 에서 미분가능하지 않을 수 있다.

[증명]

함수 f(x) = ㅣx l 를 예로 들어 봅시다.

함수 f(x)는 x = 0 에서 미분가능하지 않다. 따라서 함수 f(x) = ㅣxㅣ는 x = 0 에서 연속이지만 미분가능하지는 않습니다.

미분 계수는 함수의 극한으로 정의되어 있다. 함수의 극한에서 좌극한과 우극한이 같은 값에 수렴할 때 함수의 극한이

존재한다고 한다. 즉, 미분계수가 존재하려면 △x → 0 일 때 평균변화율의 좌극한과 우극한이 같아야 한다.

따라서 위와 같은 반례에 의해 함수의 연속성이 함수의 미분가능성을 보장하지는 않는다.

즉, 함수 y = f(x)는 x = a 에서 연속이어도 일반적은로 함수 y = f(x)가 x = a 에서 미분이 가능한 것은 아니다. 또한 위의

함수에서와 같이 x = a 에서 연속이지만 x = a 에서 뽀족하면 (부드럽지 않으면) x = a 에서 미분가능하지 않다.

이러한 점을 뾰족한 점 또는 첨점이라 고 한다.

[함수의 미분가능과 연속]

함수 y = f(x)가 x = a 에서 미분가능하면 함수 y = f(x)는 x = a 에서 연속이다.

그러나 그 역은 일반적으로 성립하지 않는다.

[위 명제의 대우]

'함수 y = f(x)가 x = a 에서 연속이 아니면 함수 y = f(x) 는 x = a 에서 미분가능하지 않다' 도 성립한다.

[이차함수 접선의 기울기]

미분방정식은 순간변화율을 나타내는 방정식이다. 우리가 일상생활에서 사용하는 속도라른 개념은 거리를 시간으로

미분한 개념이고 가속도는 속도의 변화율을 말하는 것으로 미분의 개념을 포함하고 있다.

수학에서는 도함수를 포함하는 방정식을 미분방정식이라고 한다.

도함수가 몇 차이냐에 관계없이 포함하면 미분방정식이다.

만약 y의 도함수를 포함한다면 미분방정식을 풀어 해를 구한다는 것은 y라는 함수를 구한다는 것이다.

당연한 말이지만 이런 방정식을 구한다는 것은 x를 구한다는 것이다.

그런데 미분방정식에서는 다음과 같이

이런 식이 된다. 이는 y"는 y라는 함수를 두번 미분한다는 것이고 y'는 한번 미분한다는

것인데 여기서 y를 구하는 것이 미분방정식을 푸는 미분방정식은 여러가지 형태로 표현을

하는데 미분방정식을 해법은 이들 방정식을 풀이하는 과정이다.

위의 미분방정식은 상미분 방정식이라고 한다. 위 방정식에서는 독립변수가 하나 (①은

독립변수 x, ②는 x, ③은 t)인 경우에 종속변수가 하나 이상인 경우를 상미분 방정식이라

한다. 즉, 하나의 독립변수로 미분을 하는 경우를 상미분이라 한다.

위 의 방정식은 편미분방정식이라고 한다. 독립변수가 2개 이상인 미분방정식을 편미분

방정식이라고 한다. ④, ⑤ 식 모두 독립변수가 x, y 2개 이고 x에 대하여도 미분하고, y에

대하여도 미분을 해야 한다. 편미분에서는 x에 대하여 미분할 때는 y는 상수 취급하고 y에

대하여 미분할 때에는 x를 상수 취급을 한다. 예를 들어 마라톤 선수가 달리기를 할 때 속도

는 바람과 기온의 영향을 받는다고 하면 바람변화에 대한 속도, 기온변화에 대한 속도의

편미분 방정식이 성립하게 되는데 이 때 바람에 대해 미분할 때는 온도는 상수가 되고, 온도

에 대하여 미분할 때는 바람은 상수가 된다. 영어로 표현하면 다음과 같다.

상미분 : Odinary Differential Equation (ODE)

편미분 : Partial Differential Equation (PDE)

도함수는 y', y"로 표현했고 dy/dx로 나타낸다. 이들 두 기호를 모두 사용하는데 4계 도함

수 부터는 다음과 같이 표현한다.

물리학에서는 독립변수로 시간 t를 사용하는 경우가 많은데 이 때 "도트"를 이용하여

도함수를 표현하기도 한다.

위 식은 x라는 위치를 시간에 따라 두번 미분한다는 의마에서 점을 두개 찍어 나타낸다.

위 식은 2계 1차 미분 방정식이라고 하는데 계는 최고계 도함수의 계수를 의미한다.

최고계는 y를 x에 대하여 2번 미분하는 식이므로 여기서 최고계의 계수 2번 미분 즉 2가

된다. 차수는 최고계 도함수가 몇 제곱함수이냐를 말하는데 위 식에서는 최고계 도함수의

차수가 1제곱 함수이므로 1차 방정식이 된다.

그럼 다음 미분방정식의 도함수는 몇 계, 몇 차 도함수일까 ?

최고계 도함수의 계수가 2차이고 차수가 3이니까 2계 3차 미분방정식이라 할 수 있을까?

우변에 루트식이 있으니 이를 정수식으로 풀어줘서 차수를 결정해야 한다.

따라서 양변을 제곱을 하면 다음과 같이 되겠다.

이제 계수와 차수를 말할 수 있겠네요. 2계 6차 미분방정식이 된다. 미분방정식은 표현방법

이 여러가지여서 행태는 다르지만 같은 미분방정식이 되는 경우가 있다. 다음 식을 보자.

다음은 선형 미분방정식에 대하여 알아 보자

선형미분방정식은 도함수가 1차 선형방정식으로 표현되는 경우이다. 미분, 도함수 즉,

기울기가 직선으로 독립변수와 종속변수간에 비례관계에 있는 경우를 선형 미분방정식

이라 한다. 수치적으로 이야기하면 첫째, 종속변수 y와 모든 도함수 y', y"의 차수가 1차이

고 둘째, y, y', y"의 계수는 독립변수 x에 의존하는 이들 두 조건을 충족해야 한다.

이 미분방정식은 y'의 차수가 1차이고 계수가 4x이므로 x에 의존하는 상황이고 역시 y의

계수가 1 이므로 y에 관계없는 상황이므로 선형미분방정식이 된다.

y" + 2y'+y=0 이라는 미분방정식이 있다면 y"의 차수가 1차이고 계수가 y에 관계없고

y'의 차수도 1차 이고 계수도 -2가 되므로 y에 관계없으며 y도 마찬가지 이므로 선형방정식

이다.

위의 식들은 비선형 미분방정식이다. ①은 y의 계수가 y와 관계가 있고 ②는 y의 계수가

sin(y)이고 ③은 y의 차수가 2차 이므로 비선형 미분방정식이다.

미분방정식의 해는 미분방정식에 그 값을 대입했을 때 방정식이 성립하고 참을 이룬다.

어떤 x에 대한 방정식에서 x=3이 해임을 증명하려면 방정식에 x=3을 대입했을 때 방정식

이 성립하면 그 방정식의 해임을 증명하는 것이다. 미분방정식에서도 마찬가지이다.

미분방정식의 해가 되려면 그 해는 미분 가능해야 되므로 연속이어야 한다. 미분방정식을

풀고 나면 일반해, 특수해, 즉 General solution과 Particular solution으로 나뉘는데

일반해의 경우 해를 구하고 나서 상수가 남아 있는 경우를 말하고 특수해는 해를 구했을 때

상수가 남아 있지 않는 경우를 말한다.

어떤 미분방정식을 풀어서 해를 구했더니 상수가 들어 있다면 그것은 일반해이고, 문제에서

주어진 초기조건을 대입하여 상수를 찾아서 해를 구했다면 이는 특수해이다. 특히, 물리학이나 공학에서는

특수해를 구하는 것이 중요하다. 예를 들면 어떤 물체가 처음에 정지해 있었다는 초기조건을 쉽게 볼 수 있는데

그런 특수조건을 이용해서 특수해를 구하게 된다.

특히, 미분방정식에서 도함수의 계수와 임의의 상수의 개수가 일치한다. 2계 미분방정식

이면 임의의 상수가 2개가 나와야 하므로 특수해를 구하기 위해서는 초기조건도 2개가 필

요하고 3계면 3개의 상수가 나온다.

이런 경우도 있다. 어떤 미분방정식을 풀었는데 일반해도 구했고 초기조건도 구해서 풀었는

데 잘 살펴보니 y=0도 해가 되는 경우가 있다. 그런데 y=0이라는 해는 일반해의 C에 어떤

값을 넣더라도 나올 수가 없다. 이런 경우 y=0은 일반해도 아니고 특수해도 아닌데 이런 경

우를 '특이해'라고 한다. (Singular solution). 비선형 미분방정식에서는 특이해가 자주

나타난다.

어떤 미분방정식을 풀었는데 2개의 해가 나왔다고 하자. 그런데 앞에서 미분방정식에서

도함수의 계수가 임의의 상수의 개수와 같다고 했다. 이 경우 2계 미분방정식이므로

임의의 상수가 2개가 나와야 하는데 해가 2개이고 임의의 상수가 각각 하나씩 나오기도

한다.

신기하게도 위식에서는 x1과 x2라는 해를 단순히 더해서 하나의 x라는 해를 만들 수

있는데 이 경우도 해는 된다.

x1과 x2 선형결합이 된 x라는 해가 해가 된다는 것이다.

이 경우도 역시 임의의 상수의 개수가 2개이다.

일반적인 경우를 생각해 보면 n계 미분방정식의 특수해를 구하기 위해서는 n계 미분방정식

을 풀어서 나온 일반해에서 임의의 상수의 개수는 n개 이므로 초기조건이 n개 필요하다는

것을 알 수 있다.

이때 초기조건에서 y에 대입하는 x값이 동일해야 한다.

이렇게 미분방정식과 초기조건을 이용해서 미분방정식의 해를 구하는 것을 '초기값 문제

(Initial value problem)이라고 한다. 미분방정식의 계수에 따라서 1개의 초기값 문제,

2계 초기값 문제... 이런 식으로 부른다.

이런 미분방정식을 풀어서 초기조건을 이용해서 특수해를 구했다고 하자.

그런데 특수해 y=1/(x2-1)의 그래프를 그려보면

위 그림이 그래프 y=1/(x2-1)라는 함수의 그래프이다. 그런데 문제에서 주어진 초기조건

을 만족하는 부분은 단지

이 부분이 된다. 초기 조건이 y(0)=1 이므로 좌표상 (0, -1)을 지나는 그래프다. '해의 그래프'이다.

'함수의 그래프'이냐 '해의 그래프'이냐의 차이점을 설명하는 부분이다.

이런 문제가 있는데 위 미분방정식의 일반해가 주어졌고 초기조건이 주어졌다. 그런데

초기조건을 대입하여 풀어보면 C1=0, C1=2 이렇게 나온다. 모순되는 결과이다. 이말은

이 미분방정식의 해가 없다는 뜻이다. 왜 해가 없다고 해야 하는가 ? 앞서 초기 조건에서

같은 x값을 대입하는 것이 중요하다고 했는데 위의 문제에서는 하나는 pi/2를 대입했고

다른 하나는 pi를 대입했기 때문에 이 초기조건만으로는 해를 구할 수 없기 때문이다.

​

#미분방정식 #미분 #편미분 #일반해 #특수해 #특이해 #독립변수 #종속변수 #도함수

#계수 #차수 #상미분 #선형함수 #비선형함수 #초기조건 #변화율 #기울기

​

​

【 뉴톤의 냉각법칙 】

​

커피온도는 몇 [℃]일 때 가장 맛이 있을까 ?

커피는 맛으로 마시는 게 아니라 멋으로 마시는 것일 수 있지만 일반적으로 70 [℃]라고

한다. 그럼 100[℃]의 커피를 맛있게 먹으려면 얼마나 기다려야 하는지 알아 보자.

뉴턴의 냉각법칙에 따르면 냉각속도 즉, 온도의 변화속도는 dT/dt는 냉각되는 물체의

온도 T와 주변의 온도 T주변온도 와의 차이에 비례한다.

이것을 식으로 나타내면 다음과 같다.​

이처럼 미분방정식이 성립된다.

이제 100 [℃]의 커피를 30[℃]의 방에 놨을 때 마시기 좋은 온도가 될 때 까지는 몇 분이나

기다려야 하는지 계산해 보자.​

T(t)를 구하기 위해 양변을 적분을 하게 되면​

위 식은 분류를 잘못했다. T는 시간에 따라 변화하는 시간 t의 함수인데

위 식에서는 우변 시간 T를 상수 취급을 하는 오류를 범했다.

온도 T와 시간 t를 따로 모아서 적분을 해야 한다.​

위 식을 적분을 해서 소요되는 시간을 계산해 낼 수 있겠다.​

분모를 미분한 것이 분자에 있으면 ln l분모l가 된다. 위식은 다음과 같이 변한다.​

정리하면 ln lT-30l = kt + C가 되니까.

이제 상수 C를 구해야 하는데 초기조건을 사용하면 된다.

처음(t=0) 커피온도가 100[℃] 즉 T(0)=100 이니까​

하지만 지금도 시간을 구하려 하니 상수 k가 있어서 조건이 하나 더 필요로 한다.

조건하나를 더 추가해 보자. 커피를 놔 두고 3분이 지났더니 커피온도가 85[℃]가

되었다고 하자. 그러면 k를 구할 수 있겠다.​

이제 커피가 70[℃]까지 식는데 소요되는 시간을 구할 수 있겠다.

커피가 100[℃]에서 70[℃]로 식는데는 약 7분 정도 소요되겠다.

​

【 리비의 탄소연대 추정정】 - 방사성 물질의 붕괴

​

탄소연대추정법은 물질속에 C14와 C12의 구성비를 근거로 방사성 동위원소인 C14의 반감기를 추정하여 연대를 추정하는 것이다.

생물의 경우 사체 내에 있는 C14와 C12의 구성비로 연대를 추정한다.

공기중에는 C14와 C12의 구성비율이 일정하다. 식물이건 동물이건 살아있는 동안에는 호

흡을 광합성 또는 음식물 섭취를 통하여 동일한 비율을 유지한다. 그런데 생물이 죽으면 호

흡이나 음식물 섭취가 중단되어 탄소공급이 끊긴다. 그런데 생물이 죽으면 C14 는 방사성

동위원소이니까 스스로 붕괴를 하지만 C12는 그대로 남아 있게 된다. 따라서 세월이 흐르

면 C14 대 C12의 구성비가 변하게 된다.

따라서 생물의 사체내에 존재하는 C14의 양이 공기중의 C14에 비해 몇 [%]나 감소했는

지 알게 되면 생물의 사망연대를 추정할 수가 있다.

그럼 어떤 생물의 사체에서 생존했을 때 있어야 할 C14의 양보다 20[%]밖에 남아 있지

않았다면 이 사체의 사망시점이 몇년 전인지 알아 보자.

C14 는 방사성동위원소로서 붕괴속도는 현재 질량에 비례한다. 이것을 미분방정식으로

나타내면 현재의 질량을 y라 하면 dy/dt =ky이 된다.​

양변에 적분을 해보자.

사망시점 t=0 에서 질량을 yo라고 하면 y(0)= yo 가 된다.​

비례상수 k를 구하기 위해서는 조건이 하나더 주어져야 한다.

또하나의 조건은 C14의 반감기는 5730년이다. 반감기는 질량이 반으로 줄어드는데 소요

되는 시간이므로 초기질량 yo 가 절반으로 줄어드는데 소요되는 시간이 5730년이다.

따라서 이를 아래식에 적용하여 비례상수 k를 구할 수 있다.​

이를 이용하여 C14가 당초 보다 20[%]밖에 남아 있지 않으므로 사망연대를 추정할 수

있다. 20 [%]는 1/5이므로 이를 위 수식에 적용하면 다음과 같다.​

#뉴톤 #냉각법칙 #미분방정식 #상수 #적분 #미분 #리비 #탄소연대추정 #방사성 #동위원소 #탄소 #반감기 #비례상수

1. 미분

​

독립변수 x가 연속적으로 변함에 따라 종속변수 y도 연속적으로 변할 때 어느 한 점에서 종속변수 변화량 Δx와 독립변수 변화량 Δy의 비율의 극한을 그 점에서의 ‘미분계수’ 또는 ‘순간변화율’이라고 합니다.

이에 비해 단순히 종속변수 변화량 Δx 와 독립변수 변화량 Δy의 비율을 평균변화율이라 하죠.

​

1-1. 평균변화율

​

x가 a로부터 a+Δx인 b로 변화될 때 함수 f(x)의 평균 변화율은 다음과 같습니다.

​

아래 [그림 1]에서 파랑색 직선의 기울기가 평균변화율을 뜻합니다.

1-2. 순간변화율 (미분계수)

(1)식에서 Δx→0일 때의 극한값이 순간변화율입니다. 수학적으로 표현하면 아래 식과 같습니다.​​

[그림 1]에서 주황색 직선의 기울기가 a인 지점에서의 순간변화율을 뜻합니다.

​

[예제1] 순간변화율​

[풀이] 아래와 같이 미분계수는 1/2이 나옵니다. 한편 풀이에서 빨강색 부분은 같은 양을 나누고 곱해주었음을 뜻합니다.​

[예제2] 도함수

[풀이] 도함수는 아래와 같이 구해집니다.​

한편, x=1에서의 미분계수를 구한고자 한다면 위의 도함수에서 x대신에 1을 대입하면 됩니다.

그러면 (E-1)식과 같이 1/2이 동일하게 구해지는 것을 알 수 있습니다.

결국 도함수를 구해 놓으면 어느 지점에서건 미분계수를 쉽게 구할 수 있게 됩니다.

​

1-4. 상미분

​

위에서 도함수를 구하는 과정을 미분이라고 했는데요. 이때 원래 함수의 독립변수가 하나인 경우 이 함수를 미분하는 것을 상미분이라고 합니다.

통상적인 미분이라는 뜻이에요.

상미분 개념은 예를 들어 어떤 기계장치의 온도가 기계로 들어가는 교류신호의 실효값에만 의존하는 경우 실효전압의 크기가 증가함에 따라 온도가 어떠한 기울기로 증가하는 지를 알고자 할 때 적용할 수 있습니다.

구체적인 예로는 위 [예제2]가 바로 상미분에 해당합니다. 예제에서 x를 교류 실효값의 크기라 생각하고 f(x)를 온도라고 생각하면 됩니다.

​

1-5. 편미분

​

상미분은 변수가 하나인 경우의 미분이라면 편미분은 변수가 2개 이상인 경우의 미분법을 말합니다.

편미분은 하나의 변수에 대해 미분할 때 다른 변수는 상수로 취급합니다.

편미분 개념은 어떤 기계 장치의 온도가 기계로 들어가는 교류 실효값뿐만 아니라 압력에도 의존한다고 생각해봐요. 그러면 실효값과 압력이 달라지면 온도가 달라지는거에요.

이때 압력을 고정하고, 즉 압력을 상수로 취급하고 실효값에 따른 온도의 기울기를 구하는 방법이 편미분입니다. 물론 실효값을 상수로서 고정하고 압력에 따른 온도의 기울기를 구하는 것도 편미분입니다.

편미분의 기호는 다음과 같습니다. 예를 들어 변수가 여러개인 함수 f를 x로 편미분하고자 한다면 아래와 같이 쓰면 됩니다.​

[예제3] 편미분​

이 함수를 x와 y에 관해 각각 편미분하여라.

​

[풀이]

먼저 x에 관해 편미분부터 하면, y를 상수로 취급하면 됩니다.

이때 상수를 미분하면 0이 되는 것을 상기하세요.​

다음에는 y에 관해 편미분하면 x를 상수로 취급하면 됩니다.

2. 미분방정식 (Differential equation)

​미분방정식이란 ‘하나 또는 그 이상의 독립변수에 관하여 하나 또는 그 이상의 종속변수의 도함수 또는 미분을 포함하는 방정식’을 말합니다.

특히 독립변수가 하나인 경우 상미분방정식(상미방, ODE, Ordinary Differential Equation), 두개 이

상인 경우 편미분방정식(편미방, PDE, Partial Differential Equation)이라고 부릅니다.

​

2-1. 상미분방정식

​

상미분방정식의 예시는 다음과 같습니다.​

(6)식을 보시면 y를 x로 미분하는 dy/dx항이 수식에 포함된 것을 볼 수 있어요.

이렇게 주어진 미분방정식을 푼다는 말은 독립변수가 x이고 종속변수가 y인 함수 y=f(x)를 구한다

는 의미로 보시면 됩니다.

​

2-2. 편미분방정식

​

편미분방정식의 예시는 다음과 같습니다.

(7)식을 보시면 u를 t로 편미분, u를 x로 편미분, u를 y로 편미분하는 내용이 포함된 방정식임을 알 수 있어요. 이렇게 주어진 편미분방정식을 푼다는 말은 독립변수가 x, y, t이고 종속변수가 u인

함수 u=f(x,y,t)를 구한다는 의미로 보시면 됩니다.

​

3. 미분방정식 구분

​

미분방정식은 다양한 모양을 가질 수가 있어요. 미분을 2번하는 방정식, 3번하는 방정식도 있을 수 있고 상미분과 편미분으로 구성된 방정식도 있을 수 있어요.

그래서 미분방정식을 구분하기 위한 이름이 있어야 합니다. 이때 사용되는 것이 미분방정식의 ‘계수’와 ‘차수’, ‘선형’과 ‘비선형’입니다.

​

3-1. 계수와 차수, 선형과 비선형

​

계수란 미분방정식에 포함되는 최고계 도함수의 계수를 말합니다.

미분이 한번인 dy/dx는 1계, d2y/dx2 는 2계가 됩니다. 미분방정식에서 주어지는 도함수의 가장

큰 계수를 기준으로 이름이 붙습니다.

또한 차수란 미분방정식에 포함되어 있는 최고계 도함수의 지수를 말합니다.

예를 들어 (y′′′)3 은 지수가 3이므로 3차가 됩니다.

선형 미분방정식은 종속변수와 그 도함수가 1차이고 각 계수가 독립변수에만 의존하는 것을 말합니다.

이에 비해 비선형 미분방정식은 종속변수와 그 도함수가 지수를 갖거나 계수가 종속변수를 포함하거나, 비선형 함수 등을 포함하는 경우를 말합니다.

​

3-2. 미분방정식 구분의 예​

(10)식에서 3계 도함수가 3제곱이므로 3차 미분방정식이 되며, 또한 이 때문에 도함수가 1차가 아니므로 비선형이 됩니다. 차수는 최고계 도함수를 기준으로 결정된다는 것을 기억하세요.​

(12)식에서 종속변수인 u가 제곱(즉, 2차)의 형태여서 1차가 아니므로 비선형 방정식이 됩니다.​

(13)식은 계수 (1−y)가 종속변수를 포함하여 독립변수만으로 구성되어 있지 않으므로 비선형이 됩니다.​

(14)식은 종속변수가 비선형함수로서 1차가 아니므로 비선형이 됩니다.

​

#미분 #방정식 #미분방정식 #편미분 #비선형함수 #선형함수 #독립변수 #종속변수 #계수 #차수

#도함수 #함수 #실효값 #상수 #변화율 #순간변화율 #접선 #기울기

1. 소거법과 피벗 (Pivot)

​

피벗을 한마디로 정의하기는 어렵습니다. 피벗의 정의를 무작정 들으면 이해하기 어려우므로 우선 아래 연립방정식의 해를 구하는 과정을 살펴 보면서 알아 보도록 하자.

이 방정식을 소거법으로 푼다고 하면 소거법은 여러가지 방법이 있을 것이다. 위의 식에 3을 곱해서 아래식을 빼서 x를 소거할 수도 있고 위에 식에 -3을 곱해서 아래 식을 더할 수도 있고 아래식에 1/3을 곱해서 위의 식에서 아래식을 뺄 수도 있고 아래식에 -1/3을 곱해서 위 아래식을 더할 수도 있다. 결국 미지수 앞의 계수의 절대값을 맞추어 주면 두 식을 더하거나 빼서 소거할 수 있게 된다.

​

그런데 앞으로, 소거법을 적용하여 연립방정식을 풀 때 피벗(Pivot)을 사용할 때는 이렇게 다양한 방법으로 하지를 않고 정하진 숫자를 곱해 더하거나 빼는 규칙에 따라 하게 된다. 이렇게 하는 이유는 랭크(Rank)와 가역성, 다각화, LU분해 등 여러가지가 연관되어 있어서 이다. 그럼 먼저 피벗을 정의를 알아 보자.

기본행연산과 행사다리꼴(REF)에 다음에 알아 보기로 하자.

첫번째 Pivot 의 정의에 주목을 하자. 내용이 이해하기 어려운데 차근차근 알아보자.

먼저 한 행에서 일차방정식의 첫번째 미지수 앞의 계수라고 했다.

에서 1행의 첫번째 미지수의 계수는 1이고 2행의 첫번째 미지수 계수는 3이니 pivot은 1,3 아닌가 생각할 수 있는데 그렇지 않다. ②를 보면 미지수 하나에 대한 Pivot은 1개라고 했다. 결론 부터 말하자면1행에 대해서 미지수 x에 대한 Pivot은 1이 맞다. 그런데 Pivot의 정의에 의하면 이 형태에서는 y의 Pivot을 찾을 수 없고 x의 Pivot만 2개 인 것 처럼 보인다. 이러한 모순은 ①을 해석하면 되는데, y의 Pivot을 구하려면 소거를 한번 해야 한다.

연립방정식을 보면 그대로 (1)식+(2)식을 해서 x값을 구할 수도 있지만 지금 방정식의 해를 찾는 것이 아니라 Pivot을 찾는 것이니 Pivot의 법칙에 따라야 한다.

(1)식에 3을 곱하고 (2)식에서 (1)식을 뺀 것으로 (2)식을 대체해 보자.

3x + 2y = 11 에서 3x - 6y = 3 을 빼면 8y = 8 이니

으로 연립방정식의 형태가 바뀐다. 즉 (2)식이 (3)식으로 대체되고 미지수 x가 소거되어 y만 남게 되고 이렇게 하여 두번째 Pivot을 말할 수 있게 되었다. 2행의 y에 대한 Pivot은

8이 된다.

​

이 과정을 보면 생소하고 까다롭게 느껴질 것이다. 첫번째 Pivot은 그냥 1행에서 x의 계수를 읽으면 되지만 두번째 Pivot을 구하는 과정은 낯설다. 익숙해지기 위해서는 우선적으로 필요한 것은 소거를 어떻게 해야 하는지 명확한 기준을 세우는 것이다. 앞으로 Pivot을 구하기 위한 소거는 다음과 같은 방법으로 한다.

①에서 말하는 미지수를 소거할 방정식은 식 (2)를 말하는 것으로 식(3)으로 만들어 x를 소거시키겠다는 뜻이다. 그 다음 ②에서, 소거할 미지수의 계수는 3이기 때문에 위 방정식 (1)의 Pivot = 1 로 나눈다. 이 값 3/1 = 3 이 승수(multiplier)이다. 마지막으로 ③의 내용은 승수에 음의 기호를 붙인 -3을 (1)식의 양변에 곱한 뒤 (2)식과 더해 (3)식을 만들라는 것이다. 그러면 Pivot을 구하는 과정이 완성된다.

x항이 소거된 식 (3)에서 등장하는 첫 미지수 y의 계수는 8이다. 이 8이 두번째 피벗(Pivot)이다. 이 형태의 연립방정식을 이제 행렬로 바꿔 보면 특징이 나타나게 된다.

바로 #계수행렬 A가 상삼각행렬 U로 바뀐다.

이 예시 뿐만 아니라 일반적으로 한 쌍의 해를 가지는 연립방정식의 행렬표현에서 소거법(Elimination)을 진행하면 n행 n열, 즉 대각성분의 위치에 Pivot 들이 놓이며 대각 성분들 아래는 모두 0으로 채워진 상삼각행렬이 만들어 진다.

​

Elimination makes Ax = b ⇒ Ux = b'

​

2. 0은 피벗이 될 수 없다.

​

가. 해가 존재하지 않는 경우 (불능)

종종 연립방정식의 한쌍에 해가 없는 경우가 있다.

이 연립방정식의 해는 없다고 한다. 행관점에서 보았을 때 두 직선은 평행하고 y절편이 달라 만나는 점이 하나도 없기 때문이다. 이것을 행렬로 바꾸면 이 방정식에 대한 소거법을 적용하면 Pivot을 구할 수 없게 된다. 소거법을 적용하면 승수는 3/1=3이고 승수의 음수값

-3을 (4)식에 곱한 뒤 (5)식에 더해 아래와 같이 (6)식을 만든다.

이를 만족하는 해는 당연히 존재하지 않으며 (6)식에서 y의 계수는 0이다. 그러나 Pivot은 "0"이 될 수 없다고 정의했으므로 이 행렬은 Pivot이 1개 밖에 존재하지 않는다.

이 경우 해가 존재하지 않게 된다.

​

나. 무수히 많은 해를 가지는 경우 (부정)

​

반면 두 직선이 y #절편 과 #기울기 가 모두 같다면 두 직선이 일치하는 관계를 가지게 되고 이 경우 연립방정식의 해는 무수히 많게 된다.

위 식에 소거법을 적용하면 해는 무수히 많지만 y의 계수는 "0"이니 두번째 Pivot은 값을 찾을 수가 없게 된다. 이 때도 Pivot 의 개수는 1개가 된다.

3. 여러가지 사각행렬에 대한 Pivot

​

위에서 설명한 방법은 정사각행렬이 아닌 행렬의 Pivot을 구할 때 난관을 맞게 된다. 열백터나 행벡터 같은 하나의 행, 열을 가진 행렬이나 정사각행렬이 아닌 사각행렬에 대한 Pivot 및 Pivot의 개수는 어떻게 구할까 ? 정사각 행렬이 아니라는 뜻은 연립방정식의 개수(=행의 개수=m)이 미지수의 개수(열의 개수=n)보다 작은 m<n과 같은 뜻이다. 이 때 부터는 결론적으로 말하면 행렬의 랭크와 기본행연산, #사다리꼴 행렬에 대한 기초 지식을 쌓은 다음 진행하는 것이 좋다. 간단히 몇가지 특징만 알아 보자.

​

가. #행벡터, #열벡터 즉 1개의 행이나 열로 이루어진 행렬의 Pivot은 1개이다. 1행의

      첫 성분이 Pivot에 해당한다.

나. #성분 이 1개 뿐인 행렬도 Pivot은 1개로 취급하고 그 성분이 Pivot이다.

다. m × n 행렬의 경우, 최대 n개의 Pivot을 가질 수 있고 Pivot을 구하려면 행사다리꼴 형

     태로 바꾸는 #소거법 을 진행하는 것이 좋다. 최대 n개라고 했지 항상 n개를 가지는 것

     은 아니어서 Pivot의 개수는 직접 구하기 보다 행렬의 랭크와 같으므로 랭크(Rank)를

     먼저 구하는 것이 Pivot을 구하는데도 수월하게 된다.

이제 Pivot에 대해 어느 정도 감을 잡았을 것이다. 그런데 연립방정식을 푸는 방법을 아는데 왜 굳이 Pivot을 배우는 걸까 ? 연립방정식의 방정식 계수 m과 #미지수 개수 n을 확장하였을 때는 소거법의 계산 횟수가 급증하기 때문이다. #이원연립방정식 까지는 소거법으로 푸는 속도가 월등히 빠른데 3 × 3 계수 #행렬 을 포함한 #연립방정식 만 되더라도 기존의 연립방정식 풀이법이 복잡해 지기 시작한다. 사실 #Pivot 을 포함한 #상삼각행렬 로 바꾸어 소거하는 방법을 ' #가우스 #소거법 ( #Gaussian #Elimination )'이라 하고 #행사다리꼴 과 같은 다른 행렬 주제와 연결된다.