아낌없이 주는 나무

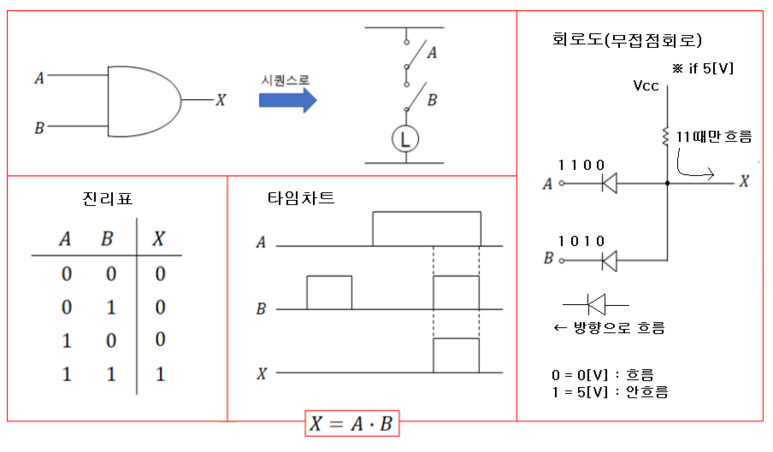
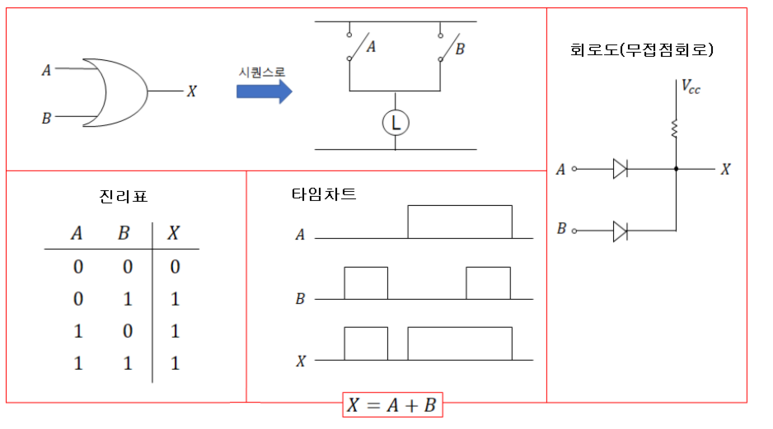
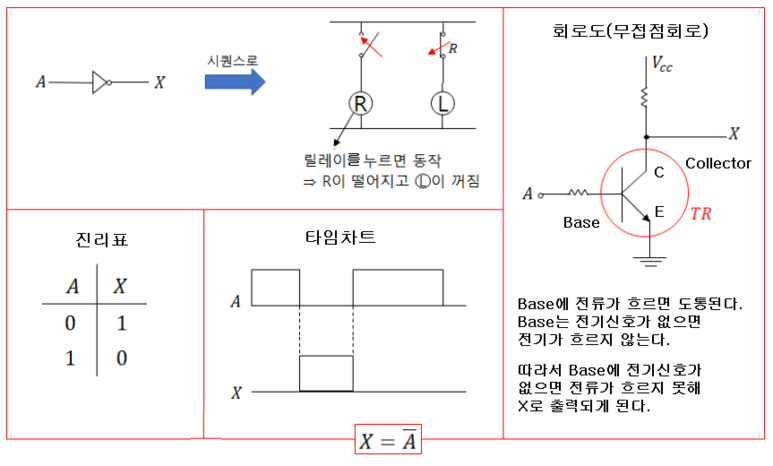
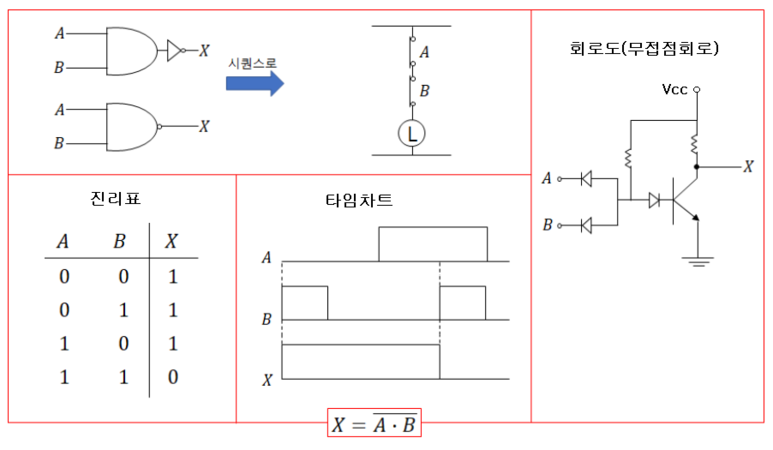
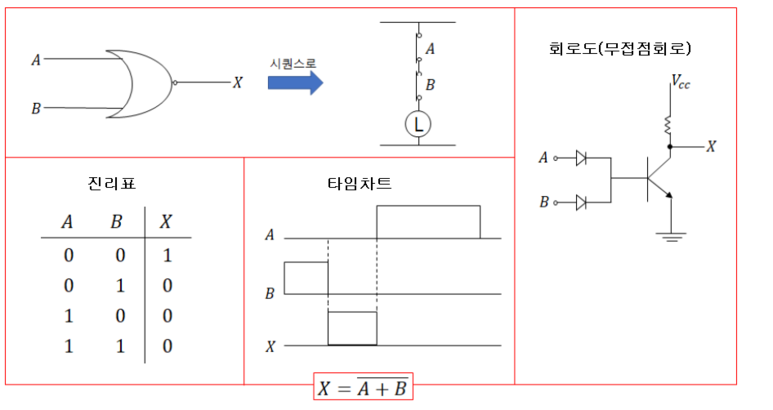
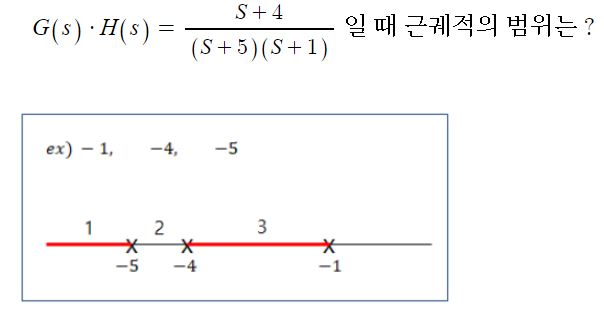
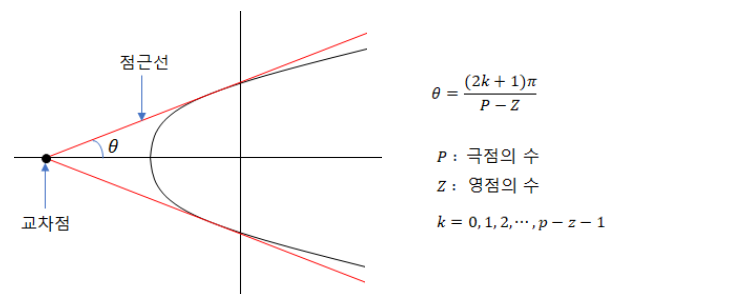
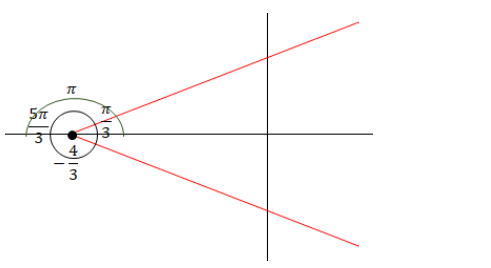
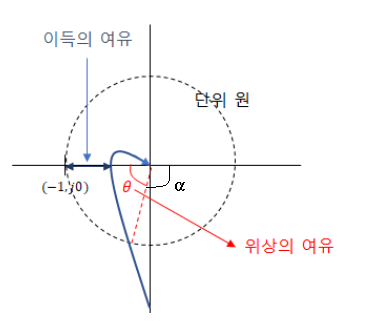
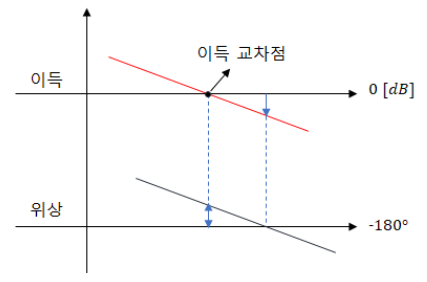
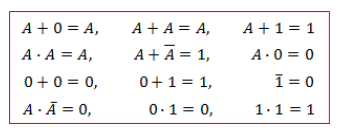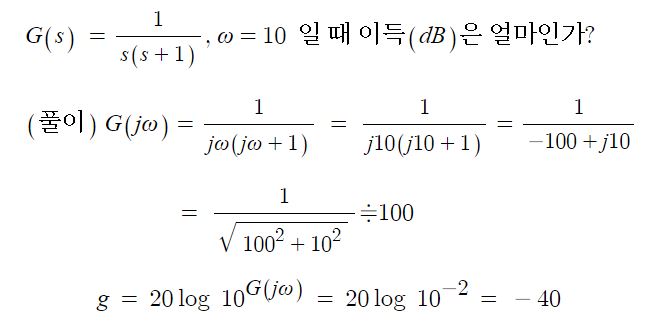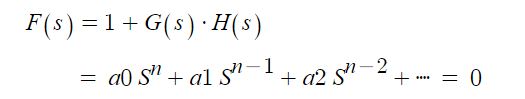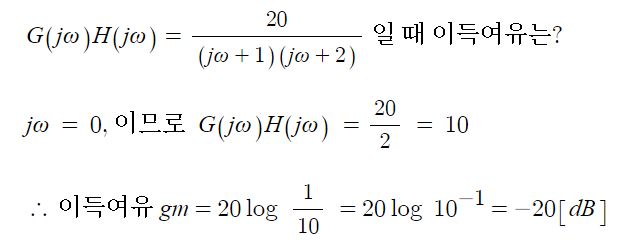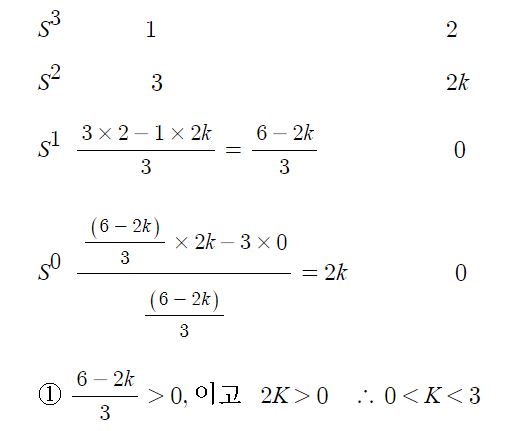PID 제어 (비례, 적분, 미분 제어)란?

​

자동제어는 감지기 및 센서로 부터의 신호를 읽고 목표치와 비교하면서

설비기기의 운전 및 정지 등 "조작량"을 제어하고 목표값에 가깝게 하는 명령입니다.

​

여기서 "조작량"을 목표값과 현재 위치의 차이에 비례한 크기로 생각하고

조금씩 조절하는 방법이 "비례 제어"라고 합니다.

​

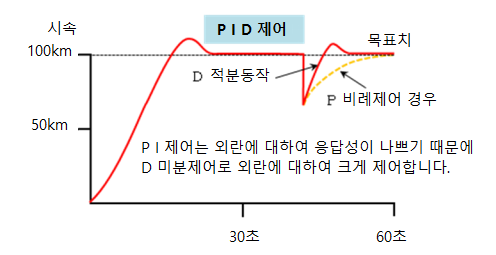
비례제어의 일반적인 제어방식으로는 "PID"가 있습니다.

​

P 동작 : Proportional 동작 (비례 동작)

I 동작 : Integral 동작 (적분 동작)

D 동작 : Differential 동작 (미분 동작)

​

1. 비례제어 방식

​

ON-OFF 제어 보다 제어 결과의 정확도를 높일 수 있는 자동제어 방식으로

비례제어 방식이 있습니다.

​

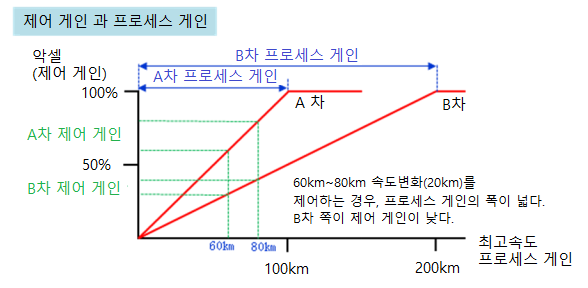
범위의 MV(조작량)가 제어 대상 PV(측정값)의 변화에 따라 0~100[%] 사이를

연속적으로 변화시키는 것을 생각한 제어방식입니다.

​

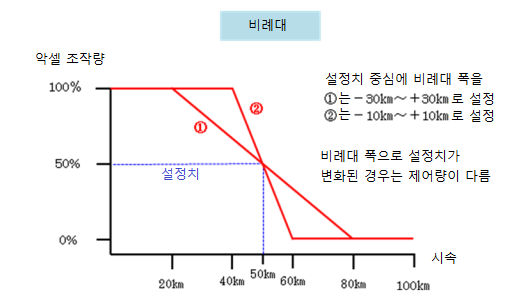
일반적으로 SV(설정값)은 비례대역의 중심에 놓습니다.

​

ON-OFF 제어에 비해 헌팅이 작고 부드러운 제어 가능합니다.

"자동차 운전"을 예로 들면, 목표값과 현재값의 차이가 크면 악셀을 더 밟아 속도를

더해가고 목표치에 가까워지면 악셀을 서서히 줄이는 것처럼 속도를 제어합니다.

​

이렇게 하면 비례제어로 잘 제어할 수 있다고 생각할 수 있지만

비례제어는 목표치에 도달하면 문제가 발생합니다.

​

목표치에 근접하게 되면 목표치와 편차가 적어, 조작량이 너무 작게 되고

더 이상 세밀하게 제어할 수 없는 상태가 되어 버려, 조작이 멈춰 버리게 되고

안정화 되어 버리는 현상이 일어나게 됩니다.

​

사람이 조작하는 경우에는 목표치에 딱 맞추는 것이 가능하지만

조절기 등을 사용하여 전기적으로 제어하는 경우에는

목표값과의 차이(편차)가 너무 작아 측정 오차 범위에 들어가 버리면

통제, 제어가 불가능한 상태가 되어 버립니다.

비례제어(P 제어)는 ON-OFF 제어에 비해 잘 제어할 수 있는 것을 생각할 수 있지만

실제로는 측정값이 설정값(목표값)에 근접하게 되면 문제가 일어 납니다.

따라서 이러한 문제를 해결하기 위해 고안한 것이

PI 제어 (비례·적분 제어) 입니다.

​

2. PI 제어 (비례·적분 제어)

​

P 제어 (비례 제어)에 있어서의 문제점은 측정값이 설정값에 도달하면 조작량이 너무 작아

제어할 수 없는 상태가 되어 버린다는 것입니다.

​

그 결과, 설정값에 매우 근접한 상태에서 더이상 조작되지 않고 안정화 되어 버려

언제까지 가더라도 "측정값 = 설정값"이 되지는 않게 됩니다.

​

여기서 P 제어(비례 제어)의 측정값과 설정값의 차이를 "e (편차)"라고 합니다.

비례제어는 목표값에 접근할 수 있지만,

목표값과의 오차(편차)는 "0"이 될 수 없는 특성을 가지고 있습니다.

​

이 편차를 없애기 위해 생각한 것이 '적분 동작(I)'입니다.

적분동작(I)은 편차를 시간적으로 축적하고 축적된 양을 설정량과 비교하여

편차를 재설정하고 편차를 없애는 방식으로 작동시킵니다.

​

이렇게 비례 동작에 적분동작을 추가한 제어를 PI 제어 (비례·적분 제어)라고 합니다.

PI 제어 (비례·적분 제어)는 P 제어( 비례 제어) 보다 잘 제어할 수 있다고 생각할 수 있지만

목표치에 맞추기 위해 편차를 축적하는 시간이 추가적으로 필요하다는 특성이 있습니다.

​

자동차 운전 제어처럼 가파른 길과 강한 역풍(맞바람) 등으로 차량 속도를 크게 방해하는

외란이 발생한 경우, PI 제어 (비례·적분 제어)는 편차를 축적하기 위해 어느 정도 시간이

소요되므로 불편한 경우가 생기게 됩니다.

​

따라서 이러한 문제를 해결하기 위해서 고안한 것이 PID (비례·적분·미분 제어)입니다.

​

3. PID (비례·적분·미분 제어)

​

PI 제어 (비례·적분)에서 개선해야 할 사항은 바로 응답시간입니다.

PI (비례·적분 제어)는 "측정값 = 설정값(목표값)"으로 제어할 수 있지만

일정한 시간이 소요됩니다.

​

예를 들어 "외란"이 있을 때, 곧 바로 반응하지 않고,

제어가 듣지 않는 상태에 빠질 수 있습니다.

​

이러한 문제를 해결하기 위해 생각한 것이 바로 "D 동작 (미분 동작)" 입니다.

​

미분 동작은 측정 시점 편차와 바로 전 측점시점간의 편차를 비교하여 그 차이로 제어하는

것으로 이를 "미분 동작"이라고 합니다.

​

이렇게 비례 동작에 적분 동작과 미분 동작을 추가한 것을 PID (비례·적분·미분 제어)라고 합니다.

​

PID (비례·적분·미분 제어)는 조작량에 민첩하고 빠르게 조작량에 반응하여

"측정값 = 설정값"이 되게 제어하는 방식이라 할 수 있습니다.​

1. 시퀀스 제어

   : 정해진 순서에 따라 차례대로 동작 (개루프 제어)

​

① 사용기구 : 입력기구, 출력기구, 보조기구

② 접 점 : 회로를 열고 닫아 회로의 상태를 결정하는 기능을 갖는 기구

  ⊙ C 접점 : a,b 변환 접점

    ◎ 유접점 : 일반적인 시퀀스 (실제 작동)

    ◎ 무접점 : 논리 작동 ( ex.. 반도체 → 논리회로 )

​

③ 수동 스위치 : 사람이 직접 누른다.

  ⊙ 회로의 개폐, 또는 접속 변경 등의 작업 명령 등의 입력 기구

      ※ BS, PB (Push Button Switch)

    ◎ 복귀형 : 누를 때 붙었다 떼면 떨어지는 것

    ◎ 유지형 : 한번 누르면 계속 유지되는 스위치

                     (보통 시퀀스 회로에서는 복귀형을 많이 쓴다)

    ◎ 검출스위치 : 온도, 열, 과전류 등을 검출하는 스위치

​

2. 논리회로

​

① AND gate

  ⊙ 입력 A, B가 동시에 있을 때 출력 X가 생기는 회로

② OR gate

  ⊙ 입력 A, B 둘 중에 하나가 있을 때 출력 X가 생기는 회로

③ NOT gate

⊙ 입력과 출력의 상태가 반대로 되는 상태의 반전 회로

④ NAND = NOT AND gate

⑤ NOR = NOT OR gate

⑥ EOR(XOR) : Exclusive OR gate

  ⊙ 입력이 서로 다를 때 출력이 나오는 회로

3. 논리 변환과 논리 연산

​

[배분법칙]

  ① A + (B · C) = (A + B) · (A + C)

  ② A · (B + C) = AB + AC

​

    (A + B) · (A + C)

      = A × A + A × C + A × B + B × C

      = A + AC + AB + BC

      = A × (1 + C + B) + BC

      = A × ( 1 ) + BC

      = A + (B · C)

    ∴ A + (B · C) = (A + B) · (A + C)

      - AB + AC = A (B + C)

​

4. 2진수의 특성

​   0 = OFF

  1 = ON

  1+1 = 1 = ON

5. 드모르간의 정리

    모든 것을 거꾸로 하면 된다.

  ◎ 상태공간법 : 현재의 회로를 바탕으로 미래를 예측하는 것

  ◎ 상태방정식 : 계통방정식이 n차 미분방정식일 때, 이것을 n개의 1차 미분방정식으로

                            바꾸어서 행렬을 이용하여 표현한 것

  ※ 미분방정식 ⇒ 3개의 1차 미분방정식 (행렬) ⇒ 상태천이방정식(상태천이행렬)

     (3차방정식)                        (상태방정식)

                       * 답 찾는 방법 정도만 다룸

​

1. 상태 방정식 

    ※ 시스템행렬과 제어행렬로 나타 내는데 시스템 행렬이 더 중요함

​◎ 상태천이방정식 : 입력 r(t)="0"이고 초기 조건만 주어졌을 때, (초기시간 이후에는

                                 어떤 현상이 나타나는가?) 초기시간 이후에 나타나는 계통의

                                 시간적 변화상태를 나타내는 행렬식

  ※ 상태천이 방정식 안에 상태천이 행렬이 있음

       상태방정식의 일반식

   ※  상태천이행렬의 성질

3. Z변환

 ※ "L" 라플라스변환 : 연속인 선형적 시스템, 규칙적 시스템

    "Z" 변환 : 불연속인 비선형 시스템, 불규칙 이산 시스템

​

① Z변환과 라플라스 변환

③ Z변화의 중요정리​

4. 가제어, 가관측

   : 제어의 기능과 불가능, 관측의 가능과 불가능을 판별한다.

1. 근궤적

S^2+3S+K = 0 이라고 할 때

  상수 K 값이 변함에 따라 근이 변하게 되는데

  근이 변함에 따라 안정 · 불안정을 판별할 수 있다.

​

   ⊙ 근 : 특성방정식의 근 - 안정과 불안정을 판별해 줌

   ⊙ S평면 상에서 개루프 전달함수(G(s)·H(s))의 이득상수 K를 "0"에서 ∞까지

       변화시킬 때 근이 그리는 궤적

       ⇒ 근궤적을 통해서 안정, 불안정을 판별할 수 있다.

​

ex) 이득상수 K의 변화에 따라 계의 특성방정식의 특성근이 어떻게 변화하는가?​

[근궤적 및 안정도]

  ① k = 0, s = -2 or 0

  ② 0 < k < 1, s = 서로 다른 음의 실근

  ③ k = 1, s = -1 (중근)

  ④ k > 1, s = 음의 공액 복소수

  ⑤ k < 0, s = 양의 실수, 음의 실근, 불안정 가능

2. 근궤적 작성 ​

 ① 근궤적의 출발 : 극점

 ② 근궤적의 도착 : 영점

 ③ 근궤적의 갯수 = 극점과 영점 중 많은 것의 갯수, 특성방정식의 최고 차수​

④ 근궤적의 대칭 : 실수축 대칭

⑤ 실수축 상의 근궤적의 범위 :

   ⊙ 극점과 영점의 총 개수가 홀수 구간에만 존재 ( - ∞ 에서 부터 시작)​

⑥ 근궤적 점근선의 각도

  ⊙ 1각도 실수축과의 내각

  ⊙ 2각도 실수축과의 외각

  ⊙ 3각도 180˚

⑧ 허수축과의 교차점 ⇒ 임계 안정 (루스표로 판별) 조건으로 계산

⑨ 이탈점, 분지점 : 특성방정식의 중근이 되는 경우

​

  ⊙ 근궤적이 나뉘어 지는 점​​

연습문제 1

문 2) G(s) = s, G(jω) = jω 의 곡선은 ?

문 3) 그림과 같은 곡선이 나오는 주파수응답은?

문 10)

       1. 모든 차수의 계수가 존재할 것

       2. 모든 차수의 부호가 같을 것 (0차는 예외적으로 봄)

       3. 루스표 1열의 부호가 같을 것

           (루스표 1열의 부호 변화 수 만큼 근이 우반평면에 존재)

  ※ 루스표 만드는 방법​

   ※ 위상의 여유와 이득의 여유

  ◎ 이득여유는 벡터궤적이 음의 실수축과 만나는 점과 판별점(-1, j0) 과 간격(차이)

  ◎ 이득 주파수 : 이득곡선과 단위 원과 만나는 점의 주파수

  ◎ 위상여유 Θ = 180˚ - α

      - 단위 원과 만나는 점과 실수축과의 각도

  ◎ 위상의 여유와 이득의 여유가 크면 클 수록 안정하다는 것

​

   ※ 이득의 여유 구하는 방법

     : G(s) · H(s)의 허수부가 0(jω=0)인 순간의 여유

예제2)​

③ 보드 선도에 의한 안정도 판별법

  ◎ 이득 교차점에서 위상이 -180˚ 보다 크고,

      위상 곡선과 -180˚선 교차점에서 이득이 음수이면 "안정"

​

※ 안정도 문제

​

문제 6) S4+2S3+S2+4S+2=0 일 때 안정도는 ?

             계수의 부호가 2번 바뀌었으므로 불안정, 우반평면에 근 2개

             ※ 차수에 "0"이 나오면 임계안정

​

문제10) 다음 전달함수일 때 안정을 위한 K의 조건은?

   G(s) = 2K / S(S+1)(S+2)

   풀이 : 1+G(s) · H(s) ⇒ H(s)=1, 단위 되먹임 함수

             특성방정식 = 개루프 전달함수의 분모 + 분자 = 0

             S(S+1)(S+2)+2K=0

            S(S2+3S+2)=0, S3+3S2+2S+2K=0​

2. 주파수 전달함수가 주어졌을 때 이득과 위상을 구하는 방법

      위상계산시 전달함수가 분모에 있을 때 위상각은 앞에 "(-)"가 붙는다.

      jb 형태시 각도는 j=90˚, -1=180˚, -j = 270˚

​

3. 벡터 궤적

  ⊙ 벡터궤적 : 주파수 전달함수 G(jω)를 복소평면상에 벡터로 나타낸 크기로서

                        G(jω)와 각도(Θ)에서 각주파수 G(jω)를 0 ~ ∞ 까지 변화시킬 때 그려진 궤적

​

                       G(jω) 에서 ω 가 0 ~ ∞로 변할 때

                      ◎ 비례요소 : k ⇒ k

                      ◎ 비분요소 : k · s ⇒ k · jω

                      ◎ 적분요소 : k / s ⇒ k / jω

                      ◎ 1차 지연 요소

                      ◎ 2차 지연 요소

                      ◎ 부동작 등

​

  ① 비례요소

      G(jω) = K​

③ 적분요소

    G(s) = k / s ⇒ G(s) = k / jω

④ 비례미분요소

    G(s) = 1+Ts ⇒ G(s) = 1+jωT

⑤ 1차 지연

4. 형에 따른 벡터 궤적 그리는 방법

※ 보드 선도에는 이득, 위상 곡선이 있음​

[이득]​

     ⊙ 절점 주파수 : 굴곡점이 발생하는 주파수

                               전달함수에서 실수부 = 허수부일 때의 주파수

     ⊙ 분자는 출발점

​

ex) 1차 지연요소 보도 선도를 예를 들면

6. 주파수 특성에 관한 상수 (용어 정리)​

   ① 영주파수의 이득 M0

        : 정상값 ⇒ 최종값의 정리

​

    ⊙ 영주파수의 이득 Mo (정상값) : 최종값 정리에 의하여 단위 계단 입력에 대한

         정상응답은 폐회로 전달함수에서 "S = 0"으로 놓았을 때 얻을 수 있는 정상값

  ② 대역폭 (BW : Bandwidth)