1. 호도법
▣ 일반적으로 평면에서 각을 표현할 때 도(degree)를 사용합니다. 하지만 이 도수법은 수
학이나 기하학에 연관되면 수식으로 연결하기 어려우므로 호도법을 사용하게 됩니다.
▣ 학교 수학에서 반지름(radius)이 1인 원의 둘레는 2π(pi, 파이)라는 것을 배웠습니다.
π는 순환하지 않는 무한소수로 원주율이라고 하며 수치로는 3.1415926...로 알고 있
습니다.
▣ 그럼, 각도가 a˚ 일 때 만들어지는 부채꼴의 호의 길이는 얼마일까요 ?

▣ 비례식을 이용하면 쉽게 풀 수 있겠지요.
360˚의 원일 때 둘레가 2π 였기 때문에 a˚ 일 때의 부채꼴의 호의 길이도 알수 있죠

▣ 하나더 응용해 보죠. 반지름이 r 일 때는 원의 둘레가 2πr입니다.
그럼 반지름이 r이고 각도가 a˚인 부채꼴의 호의 길이는 얼마일까요? 위의 식을
이용하여 구할 수 있겠죠..

▣ 거꾸로 반대 유도식도 가능하겠죠.
반지름이 r인 부채꼴의 호의 길이가 x일 때 부채꼴의 각은 얼마일까요?
이것도 비례식을 이용하면 쉽게 풀 수 있겠죠..

▣ 비례식을 이용해서 풀려면 숫자를 외워야 하고 나눗셈이 들어갑니다.
이건 매우 귀찮은 작업이며 실수의 여지도 있겠지요. 그래서 수학자들은
간편한 방법을 찾게 되었고 호도법이라는 것이 나오게 됩니다.
※ 1714년 Roger Cote라는 사람이 호의 길이를 각처럼 사용했다고 하여
붙여진 이름입니다.
▣ 호도법은 반지름이 r일 때 부채꼴 호의 길이가 r인 경우를 1라디안(radian)
이라고 표현합니다. 즉, 각도의 크기를 도수에서 길이의 단위로 바꾸버린 것입니다.

▣ 여기에서 질문이 나올 타임입니다. 대체 뭐가 편한데요?
우리는 반지름이 r인 원의 둘레가 2πr이라는 것을 알고 있습니다.
반지름이 r인 부채꼴(반원)의 호의 길이는 πr이고 각도는 π입니다.
반지름이 r인 부체꼴(반원의 반원)의 호의 길이는 1/2πr이고 각도는 1/2π입니다.

▣ 관계가 명확해 지지 않나요? 만약 반지름이 r인 부채꼴의 각도가 a라디안이라면
그것의 호의 길이는 ar인 것입니다.

▣ 복잡하게 생각할 필요가 없습니다. 각도와 반지름을 알면 호의 길이를 알 수 있고
각과 호의 길이를 알면 반지름을 알 수 있습니다. 또한 반지름과 호의 길이를
알면 각을 알 수 있습니다. 계산이 단순해지지 않습니까?
2. 입체각
▣ 평면에서의 각은 라디안이라는 단위를 사용해서 쉽게 표현할 수 있다는 것을
알 수 있었습니다. 하지만 3차원의 각도는 어떻게 표현할 수 있을까요?
우리는 각도를 평면에서만 생각했기 때문에 3차원에서 10˚라는 각도를 상상할 수 있을
까요?
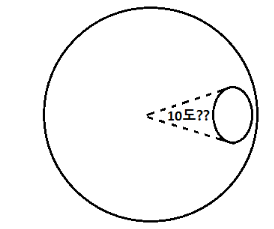
▣ 3D에 익숙한 분이시라면 이를 경도와 위도처럼 나누어 생각하실 수 있을 겁니다.
위의 그림처럼 중심이 되는 방향(벡터)를 기준으로 수평으로 몇 도, 수직으로 몇 도
이렇게 나눌 수 있겠죠. 하지만 표현은 가능하겠지만 머리만 복잡해지므로 더는 진행하지
는 않겠습니다.
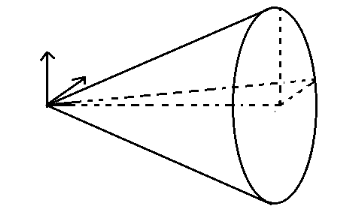
▣ 하지만 수학자들은 호도법을 발명했듯이 입체각 (Solid angle)이라는 것을 발명했습니
다. 반지름이 r인 구에서 면적이 r2인 면적을 포함하는 원뿔형의 각을 1스테라디안
(steradian, sr)이라고 부르고 이러한 각도를 입체각이라고 정했습니다.
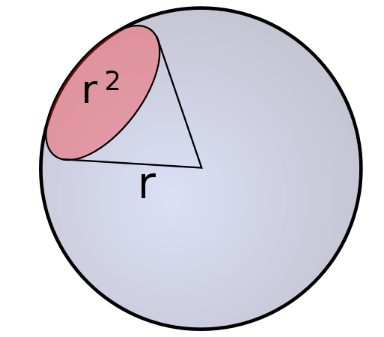
▣ 그럼 여기서 또 뭔가 보이지 않으시나요?
호도법에서 길이를 각으로 치환했듯이, 입체각은 겉넓이(면적)을 각으로 치환한
것입니다. 호도법에서는 1차원적인 곱인 "호의 길이 × 반지름" 으로 표현되듯이
입체각은 2차원적인 곱인 "겉면적 × 반지름의 제곱" 으로 표현되고 있습니다.
▣ 우리는 구의 겉면적을 4πr2 으로 알고 있습니다.
r2 이 1스테라디안을 의미하므로 구 전체의 입체각은 4π 입니다.
만약 반지름이 r인 구에서 입체각이 a [sr(스테라리안)]인 원뿔형의 겉면적을 구해야
한다면 다음과 같은 관계로 표현할 수 있습니다.
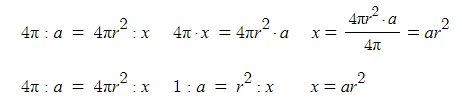
입체각도 호도법처럼 매우 단순하게 표현되는 것을 알 수 있습니다.
'생활속의 전기상식' 카테고리의 다른 글
| 2개 시설 전기안전관리자 통합 선임 가능 여부 (2) | 2025.01.24 |
|---|---|
| 공진 (Resonance)의 개념 이해.. (0) | 2023.02.12 |
| 인덕턴스 (Inductance)와 커패시턴스(Capacitance)의 개념 이해 (0) | 2023.02.12 |
| 전기기사 단답형 암기자료 (0) | 2021.10.09 |
비버리님의
글이 좋았다면 응원을 보내주세요!
