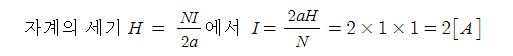1. #전류 의 자기 작용
▣ 전류의 자기 작용
⊙ 전류가 흐르고 있는 직선 도체 부근에 자침을 가까이 하면 자침은 일정한 방향으로 회전을 하고, 전류의 방향을
바꾸면 자침의 회전방향은 반전된다. 이와 같이 자침의 자극에 힘이 미치게 하는 원천은 또 다른 자계가 있기
때문으로 전류가 흐르는 도체 주위에 동심원 형태의 자계가 형성되는데 이를 전류의 자기작용이라 한다.
2. 앙페르의 오른 나사 법칙
▣ 직선 도체에 전류가 흐르면 도체 주위에 자계가 형성되는데 도체에 수직인 평면상에서 오른나사가 진행하는 방향으로
전류가 흐를 때 나사를 돌리는 방향으로 동심원의 자계가 발생한다. 즉, 전류에 자계방향의 관계를 나타낸 법을
앙페르의 오른 나사 법칙 (Ampere's right handed screw rule)이라 한다.

① 전류의 방향 : 오른 나사의 진행 방향
② 자계의 방향 : 오른 나사의 회전 방향

2. 전류에 의한 자계의 세기
가. 비오 - 사바르의 법칙
▣ 전선에 전류 I[A]를 흘렸을 때 미소부분 dl[m]에서 r[m] 떨어진 P점의 미소자계의 세기 dH[AT/m]를 정의하는 법칙

여기서, △H : P점의 미소자계의 세기 [AT/m], I : 도체의 전류 [A]
△ℓ : 도체의 미소부분[m], r : 거리 [m]
θ : △ℓ과 점 P를 연결하는 방향이 △ℓ과 이루는 각 [rad]
▣ 도선 주위의 자기장을 구하는 법칙으로 도선에 전류 I가 흐를 때, 미소 전류 Idℓ에서 r[m] 떨어진 P점에서의
미소자계의 세기

▣ 미소자계 dH는 미소전류 Idℓ에 비례하고 도선에서 거리 r의 제곱에 반비례
⊙ 도선 A점에서 B점까지 전류가 흐를 때, 자계의 세기는

나. 자계 내에서 전류가 흐르는 도체가 받는 힘
▣ 전자력 : 자계 내에 전류가 흐르는 도체가 있을 경우, 도체가 받는 힘 (전동기의 동작원리)
▣ N극과 S극이 만드는 자계와 전류에 의한 자계의 상호 작용에 의해 자계의 합성이이루어지고, 전류가 흐르는 도선은
힘을 받게 됨 (도선 아래의 자속밀도가 위쪽에 비해 높으므로)

※ 도체에서 형성되는 자기장이 자석에서 나오는 자기장이 상호작용을 해서 위쪽은 서로 상쇄되어 자기장이 약하고
아래쪽은 더해져 자기장이 강하게 된다.
▣ 이 때 힘의 크기는 전류 I, 도선의 길이 ℓ, 자속밀도 B에 비례하며, 전류의 방향과 자계의 방향이 형성하는 각도를
θ라고 하면 힘의 크기는 다음과 같이 구할 수 있다.

나. 원형 코일 중심의 자계
▣ 철가루를 뿌렸을 때의 모양 : 원형 도선의 각 부분을 작은 직선 도선으로 생각했을 때 각 직선도선의 자기력선이
합해진 모양으로 도선 중심에서는 일직선이 된다.
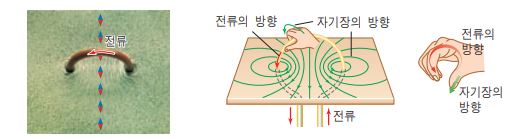
▣ 자기장의 방향 : 원형 도선의 중심에서 자기장의 방향은 오른손 네 손가락을 전류의 방향으로 감아쥘 때
엄지손가락이 가리키는 방향이 된다.
▣ 원형 도선 중심에서 자기장의 세기 : 도선에 흐르는 전류의 세기에 비례하고 도선의 반지름에 반비례한다.
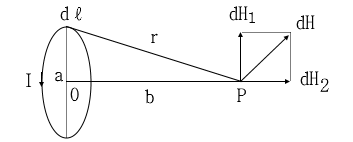
P점에서 자계의 세기는 다음과 같이 구할 수 있다.

다. 암페르의 주회적분 법칙
▣ 암페어의 오른손 법칙을 이용하여 전류분포가 대칭적일 경우 전류에 위한 자계를 구하는 법칙
▣ 폐곡선 C에 대한 자계 H의 선적분은 이 폐곡선과 쇄교하는 전류의 합과 같다.
(도체 C에 흐르는 전류에 의해 생성되는 자계 H의 총합은 도체에 흐르는 전류의 총합과 같다.)
▣ 코일 1턴(Turn)의 경우
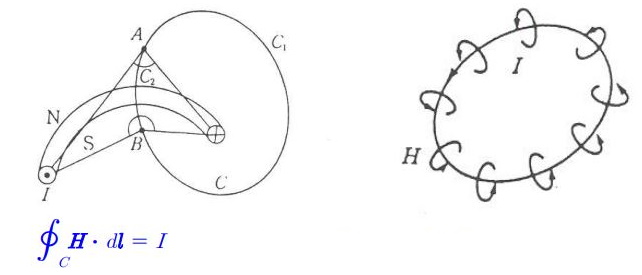
▣ 코일이 N턴인 경우
라. 무한장 직선 전류에 의한 자계의 세기
▣ 무한히 긴 직선 도체에 I [A]의 전류가 흘렀을 때 점 P에서의 자계의 세기
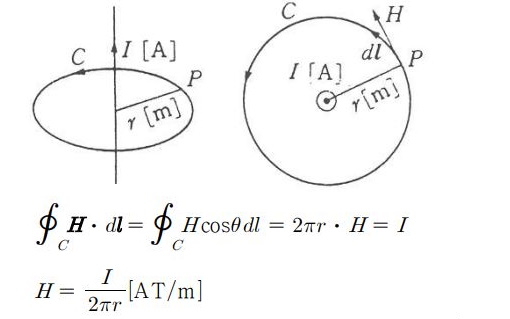
▣ 무한장 직선 도체에 흐르는 전류에 의한 자계의 크기는 전류에 비례하고 직선 도체와의 거리에 반비례한다.
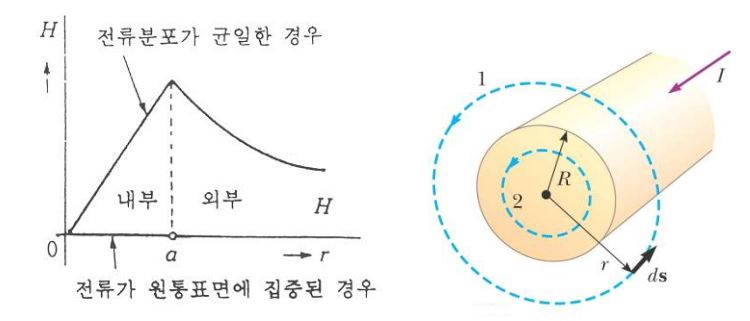
▣ 원주형 도체의 내부에 전류 분포가 균일한 경우 도체 반지름이 a이라고 하면 a = r 일 때 자계의 세기가 가장 크다.
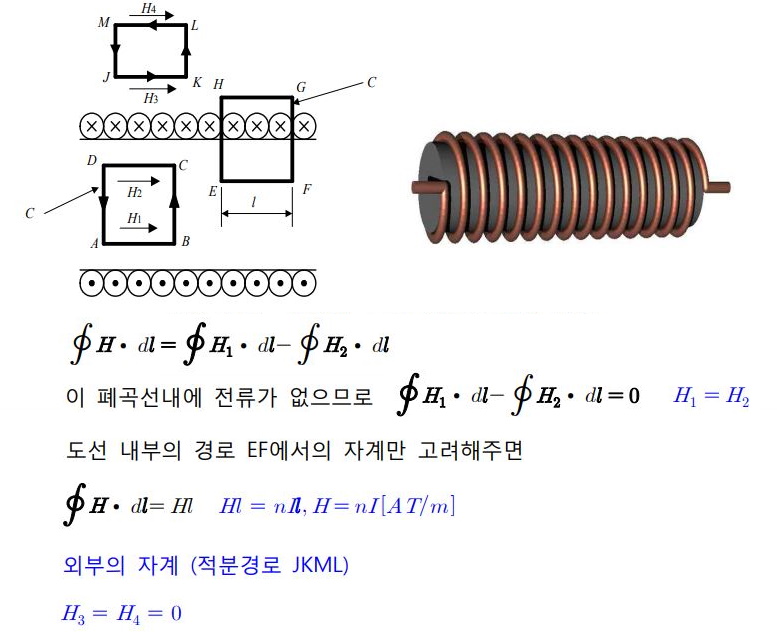
마. 무한장 솔레노이드에 의한 자계의 세기
▣ 원통형 도체에 단위 길이 당 n회의 코일을 감은 형태
① 솔레노이드(Solenoid) 내부의 자계
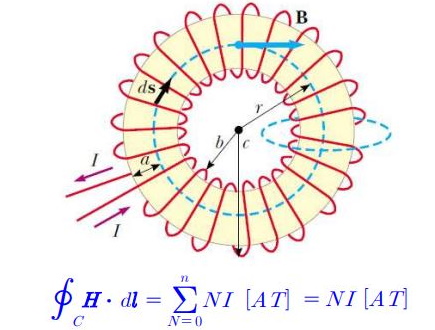
바. 환상 솔레노이드에 의한 자계의 세기
▣ 환상 솔레노이드 (토로이드) : 원형 철심에 코일을 감은 것
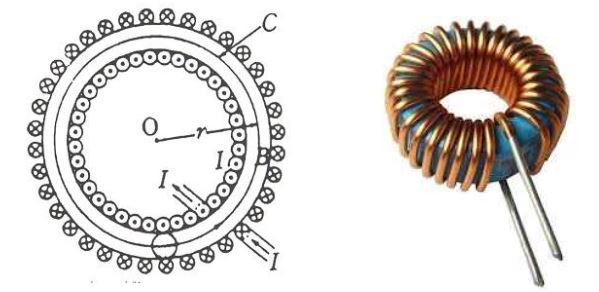
▣ 권수 N의 환상 솔레노이드에 전류 I[A]가 흐를 때 적분 경로 C에서의 자계의 세기

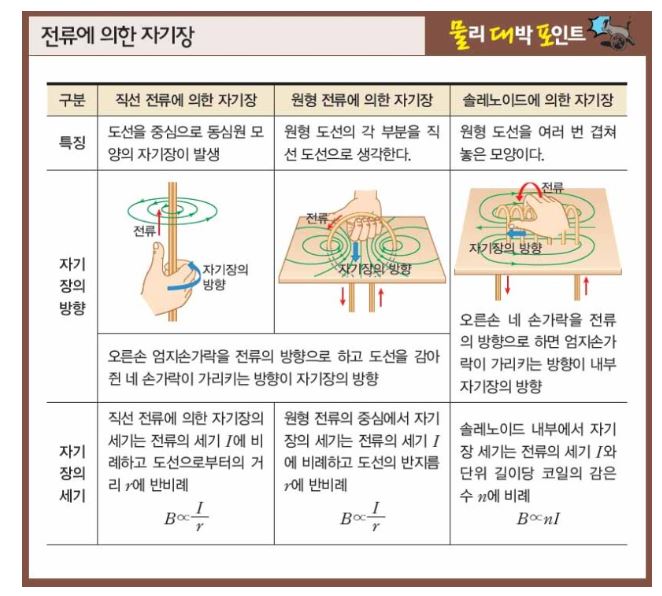
【 출제 예상 문제】
1. 전류에 의한 자계의 세기를 구하는 법칙은 ? ③
① #쿨룽 의 법칙 ② #페러데이 의 법칙 ③ 비오-사바르의 법칙 ④ #렌츠 의 법칙
[해설] 비오-사바르의 법칙 : 전류에 의해 발생되는 자기장의 크기 (전류에 의한 자계의 세기)
2. 전류의 자기작용에서 전류에 의한 자계의 방향을 결정하는 법칙은 ? ①
① #앙페르 의 오른 나사 법칙 ② 플레밍의 오른손 법칙
③ #플레밍 의 왼손 법칙 ④ 페러데이법칙
[해설] 앙페르의 오른 나사 법칙 : 전류에 의한 자계의 방향을 결정하는 방식
3. 코일의 권수가 1.250회인 공심 환상솔레노이드의 평균길이가 50[㎝]이며, 단면적이 20[㎠]이고,
코일에 흐르는 전류가 1[A]일 때 솔레노이드의 내부자속은 몇 [Wb]인가 ?

4. ㎝ 당 권수가 100인 무한장 솔레노이드에 2[㎃]의 전류가 흐른다면 #솔레노이드 내부의 자계의 세기[AT/m]는 ? ③
① 0 ② 10 ③ 20 ④ 50
[해설] 무한장 솔레노이드에 의한 자계
H = nI =100 × 100 × 0.002 = 20 [AT/m]
5. 반지름 5[㎝], 권수 200회인 원형 코일에 2[A]의 전류를 흘릴 때 코일 중심의 #자기장 의 세기 [AT/m]는 ? ④
① 200 ② 400 ③ 2,000 ④ 4,000
[해설] 원형 코일 중심에서의 자계의 세기
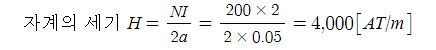
6. 무한장 직선도체에 1[A]의 전류가 흐른다. 이 때 생기는 자계의 세기가 0.2[AT/m]인 점은 도체에서 몇 [m] 떨어진
점인가 ? ②
① 5/π ② 5/2π ③ 5π ④ 10π
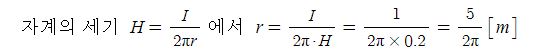
7. 공기중에 100[A]의 전류가 흐르는 도체와 직선거리로 0.5[m] 떨어진 곳에서의 자기장의 세기는 약 몇 [AT/m]인가 ? ①
① 31.8 ② 25 ③ 50 ④ 63.7
[해설] #비오-사바르 의 법칙
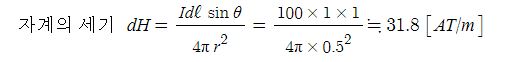
8. 반지름이 1[m]인 #원형코일 에서 중심점에서 자계의 세기가 1[AT/m]라면 흐르는 전류는 몇 [A]인가 ? ②
① 1[A] ② 2[A] ③ 3[A] ④ 4[A]
[해설] 원형코일 중심에서의 자계의 세기
'소방설비기사 (전기) > 소방전기일반' 카테고리의 다른 글
| 전자 유도 현상 : 패러데이의 법칙 등.. (0) | 2023.02.07 |
|---|---|
| 전자력 : 자기장 내에서 도체가 받는 힘 (0) | 2023.02.06 |
| 자기회로 - 정자계.. (2) | 2023.02.01 |
| 전계와 전기력선 - 정전계 (2) | 2023.01.30 |
| 콘덴서와 정전용량 - 정전계 (1) | 2023.01.30 |
비버리님의
글이 좋았다면 응원을 보내주세요!