【 가우스 정리】
▣ 대칭 전하 분포에 의한 전계의 세기를 구할 때 사용한다.
가우스의 법칙하면 전계의 세기와 연관하면 된다.
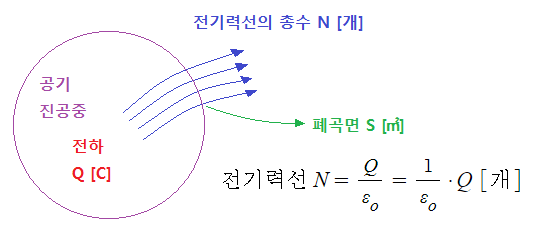
▣ 정의 : 임의의 폐곡면(S)을 통해 나오는 전기력선의 총수는 그 폐곡면 안에 있는
전하 (Q)의 1/εo 배와 같다.
※ 가우스의 법칙은 어느 공간에 구형태의 공간을 가정한 다음에 그 공간 구의 체적에서
발산하는 자기력선과 구의 표면에서 나오는 자기력선은 같다는 정리로 부터 자기력선의
밀도 즉 전계의 세기를 구하는데 사용된다.
구의 체적에서 전기력선의 발산을 구한다든지, 구의 표면에서 면의 단위면적당 전기력선의
밀도를 구한 다음 이를 적분하여 전계의 세기를 구하게 된다.
※ 구의 체적에서 전기력선의 발산을 구한다든지 구 표면의 전기력선을 밀도를 통해 전계의 세기를
구할 때 면적분과 체적적분을 사용하기 때문에 이를 이를 가우스법칙의 적분형이라 한다.
※ 또한 전계의 세기는 거리의 제곱에 반비례하고 어느 공간상에서 Q[C]이 있을 때 이로 부터
r[m] 떨어진 곳의 +1[C]이 받는 힘인 전계의 세기는 Q[C]를 거리의 제곱으로 나누어 주게 되고
유전율이란 1[m]에 1[V]의 전위차를 발생시키기 위한 전하량이라고 정의할 수 있으므로
전계의 세기는 다시 유전율로 나눠주면 된다. 따라서 아래와 같이 전기력선의 밀도를 구할 수
있는데 이를 가우스 법칙의 미분형이라 부른다.
① 가우스 법칙의 적분형
▣ 전기력선의 총수
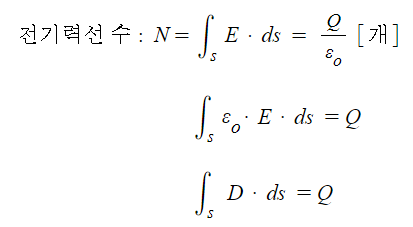
⊙ 특정 지점에서 구의 표면에서의 단위 면적당 전기력선의 밀도를 적분을 하게 되면 전체 전기력선의
총수를 구할 수 있다. 이 전기력선의 수는 전체 전하량을 유전율로 나눈 값과 같게 되는데
양변을 유전율로 나누어 주게 되면 유전율 × 전계의 세기란 좌변의 식을 구할 수 있다.
이는 전속밀도와 같게 되므로 구 표면의 전속밀도를 적분하게 되면 결국 총 전하량이 된다.
② 가우스 법칙의 미분형
▣ 전기력선의 총수 N


적분기호를 제거하게 되면 가우스의 미분형을 취할 수 있다.
【 포아송과 라플라스 방정식】
① 가우스 법칙의 미분형
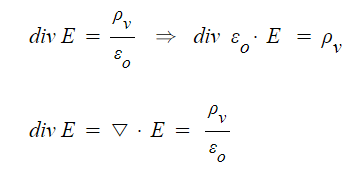
▣ 가우스법칙 미분형에서 전계의 발산은 특정 공간에서 체적전하 밀도를 유전율로 나눈 값과 같게되고
양변에 유전율을 곱해 주면 체적전하밀도는 전계의 발산에 유전율을 곱해주는 값이 된다.
② 전계의 세기 : E = - grad V = - ▽·V

※ 전계의 발산에서 전계 E는 - grad V로 바꿔 쓸 수 있고 이는 체적전하 밀도를 유전율로
나눈 값과 같게 된다. div는 ▽·로 바꿔 쓸 수 있고 grad 도 ▽로 쓸 수가 있다.
▽제곱은 라플라시안이라 부르기도 한다.
▣ 포아송 방정식의 용도

⊙ 체적전하밀도 (ρv)가 공간적으로 분포되어 있을 때 그 내부 임의의 점에서
전위(V)를 구하는 식이다.
⊙ 전위함수(V)가 주어지고 체적전하밀도 (ρv)를 계산할 때 사용한다.
※ ▽2 라플라시안이라고 함

※ 즉 (x, y, z) 축 방향에 대해 편미분을 2번 하라는 명령어다.
【포아송 방정식 예제】
예제 1. 전위함수 V = x2 + y2 [V]를 형성하는 전위분포에서 1[㎥]안의 전하밀도
[C/㎥]를 구하면 ?
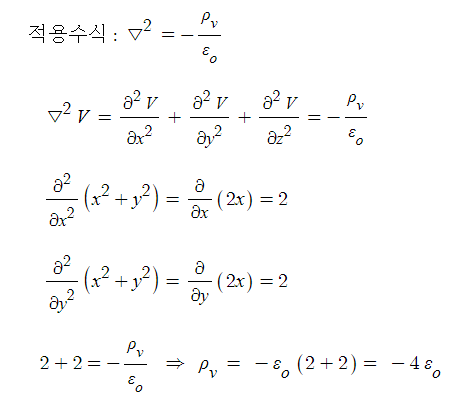
예제 2. 포아송의 방정식에서 전하가 분포되어 있지 않은 곳에서 라플라시안 ▽2=0이다.
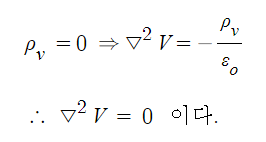
【공식정리】
1. 전위 경도
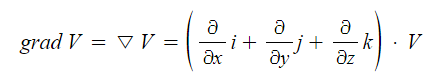
※ 전위경도는 전위의 기울기를 말하는 것으로 전위를 편미분하라는 의미이다.
편미분의 결과는 벡터로 표시되며 전위를 x, y, z 축에 대하여 편미분하면 된다.
2. 전계의 세기
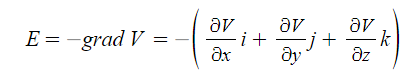
※ 전계의 세기는 전위 경도에 - 이다. 여기서 - 는 방향이 반대라는 의미이다.
전계의 세기는 전위와는 반대방향으로 나타난다는 의미이다.
즉 전계의 세기는 전위를 편미분하여 - 부호를 붙이면 된다.
3. 발산정리 (면적분 ↔ 체적적분)
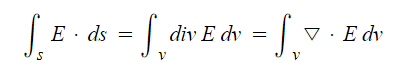
4. 전계의 세기와 전속 밀도 : D = εo · E
※ 전계의 세기에 유전율을 곱하게 되면 전속밀도가 된다. 전계의 세기는 결국 특정 지점에서
유전율로 나눈 값이 되므로 결국 전속밀도는 전계의 세기에 유전율을 곱한 값이 된다.
5. 가우스 법칙 : 전계의 세기를 산정하는 식
① 가우스법칙 적분형
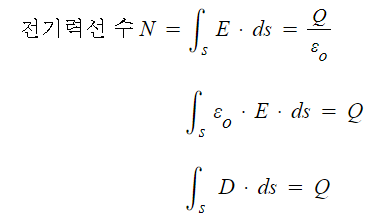
▣ 전기력선의 수는 구의 표면의 단위 면적당 전하밀도를 적분한 값이 되며
결국 전속밀도의 적분값이 총 전하의 값과 같게 된다.
② 가우스법칙 미분형
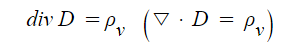
▣ 전속밀도 (전하량)의 발산은 체적 전하밀도와 같다. 체적전하 밀도를 전속밀도로
말을 바꾼 것과 같다.의미이다.
6. 포아송의 방정식
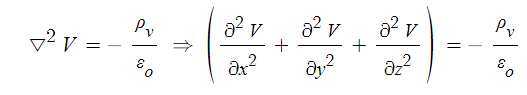
▣ 포아송의 방정식은 전위를 x, y, z 축에 대하여 2번 편미분하라는 의미이다.
7. 라플라스방정식
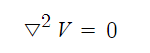
※ 어떤 공간내에서 전하량이 존재하지 않는 곳에서의 전위를 두번 편미분하게 되면
"0"이 된다는 의미있다.
'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 전기장과 전기력선에 대하여 (0) | 2024.08.05 |
|---|---|
| 전자기학 핵심요약 정리 - 전기기사 (0) | 2023.04.29 |
| 벡터의 적분, 발산 정리 - 전자기학 (0) | 2021.11.12 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
