【벡터의 적분】 ⇒ 적분은 더한다는 의미 : ∫ : Sum의 의미
① 적분기호 : ∫ : sum의 S 기호화한 것이다. 즉 적분은 더하라는 의미를 기호화 한 것이다.
② 선적분 : 선의 길이를 구할 때 사용, 기호 : ∫l, ∫c, ∮, ∮c
③ 면적분 : 면적을 계산할 때 사용 : ∫s : S : square. 면적분의 S는 면적을 의미한다.
④ 체적적분 : 체적(부피)을 구할 때 사용 : ∫v : v : volume 체적적분의 v는 부피를 의미한다.
【전하 밀도】
▣ 일정한 길이(선)나 넓이(면) 또는 부피(체적)에 존재하는 전하(Q)의 총량을 말한다.
※ 단위 길이, 넓이, 부피 당 전하량을 의미한다. 밀도를 구하는 것은 전체 중 일부분에 대한
단위당 밀도를 구해서 전체의 양을 구하기 위해 산정하게 된다.
1. 선전하 밀도
① 기호 : ρl, = λ : 단위 길이당 전하량
▣ 선전하 밀도의 기호는 ρl, λ로 표시한다.


※ 적분식의 의미는 ① dl : 단위 길이에 대한 선전하밀도 ρl를 ② 전체 길이 L이 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식은 선전하밀도에 전체 길이를 곱한 값과 같게 된다.
2. 면전하 밀도
① 기호 : ρs, : 단위 면적당 전하량


※ 적분식의 의미는 ① ds : 단위 면적에 대한 면전하밀도 ρs를 ② 전체 면적 s가 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식은 면전하밀도에 전체 면적을 곱한 값과 같게 된다.
3. 체적전하 밀도
① 기호 : ρv, : 단위 체적당 전하량


※ 적분식의 의미는 ① dv : 단위 체적에 대한 체적전하밀도 ρv를 ② 전체 체적 v가 될 때까지 ③ ∫ : 더하라
라는 의미이다. 따라서 위의 식 체적전하밀도에 전체 체적을 곱한 값과 같게 된다.
[종합 총 전하량]
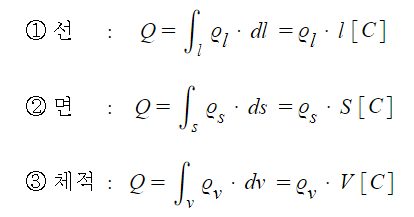
▣ 전기력선의 성질
⊙ 어느 점에서의 전기력선의 밀도는 그 점에서의 전계의 세기로 정의한다.
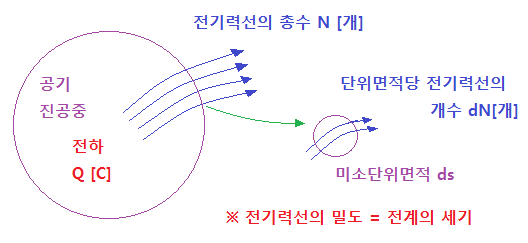
▣ 진공중에 전하 Q[C]의 전하가 있다고 할 때 이 전하로 부터 전기력선이 발산을 하게
된다. 이 전하에서는 N [개]의 전기력선이 발산하게 되고 특정 지점에서의 전기력선은
dN [개]가 된다. 특정 지점의 단위면적당 전기력선의 개수 즉 전기력선의 밀도가 그 점
에서의 전계의 세기가 된다.
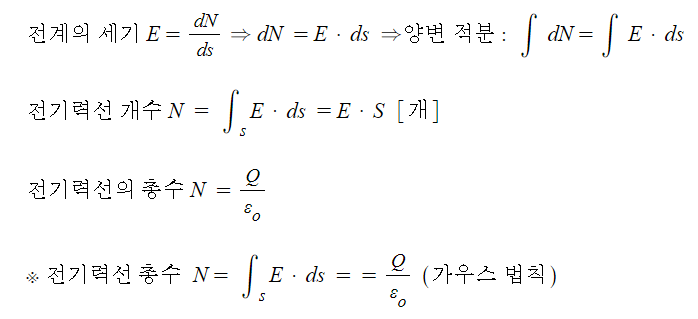

【 발산 정리 】
가. 면적분과 체적적분의 변환에 관계를 나타낸다.
나. 임의의 폐곡면의 표면을 뚫고 나오는 전기력선의 총수는 이 폐곡면에 둘러 쌓여진
체적속에서 빠져 나오는 전기력선의 총수와 같다.
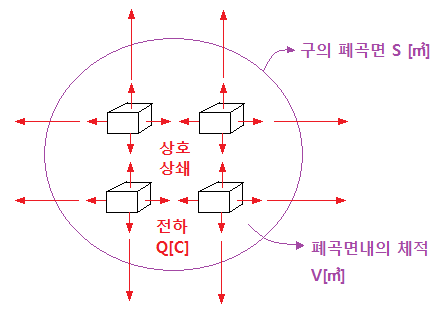
※ 단위 체적당 전기력선의 수를 면당 1개로 가정한다면 단위 체적 내부에서는 상호
전기력선이 상쇄되고 바깥면에서만 전기력선이 나오게 된다.
따라서 구의 내부에서는 전기력선이 발생하지 않게 되며 이로 인해서
구의 체적내에서 나오는 전기력선의 수와 구의 바깥면에서 나오는 전기력선의 수는
같게 된다.
【 발산의 수식 정리 】
① 면에서 빠져 나가는 전기력선의 총수

② 체적에서 빠져 나가는 전기력선의 총수
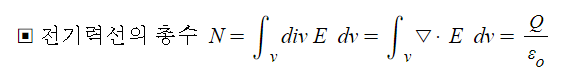
[발산의 정리 : 수식유도]

'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 전자기학 핵심요약 정리 - 전기기사 (0) | 2023.04.29 |
|---|---|
| 가우스 정리, 포아송 방정식, 라플라스 방정식, 공식정리 (2) | 2021.11.14 |
| 전속과 전속밀도 (0) | 2021.11.11 |
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
