미분이란 변화율을 의미한다. 속도와 같이 시간의 변화에 따른 위치의 변화율과 같이 속도라는 말에는 미분의 개념이
포함되어 있다. 풍속 60m/초라고 하면 이말에도 움직인 거리을 시간으로 미분했다는 말이 포함된다.
미분은 아이작 뉴턴이 운동법칙을 연구하기 위해서 미분이라는 개념을 고안해 냈다고 한다.
물체의 운동에 있어서 속도는 시간의 변화에 대한 위치의 변화율인데 이러한 변화율을 다루는 수학영역을
미분(微分, Differential calculus)라고 한다.
1. 평균변화율과 미분계수
가. 평균변화율
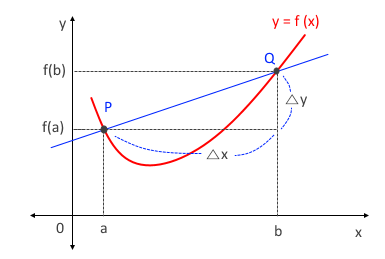
일반적으로 함수 y=f(x) 에서 x의 값이 a 에서 b 까지 변할 때, y의 값은 f(a)에서 f(b)까지 변한다.
이 때, x의 값의 변화량 b-a를 x의 증분이라 하고 △x로 나타낸다. 여기서 △는 차이를 뜻하는 Difference의 첫글자 D에
해당하는 그리스 문자로 델타 (Delta)라고 읽는다. 또, 이에 대한 y의 값의 변화량 f(b) - f(a)를 y의 증분이라 하고
△y 로 나타낸다. 즉
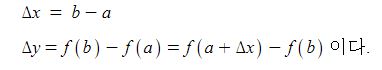
또한 x의 증분에 대한 y의 증분의 비율
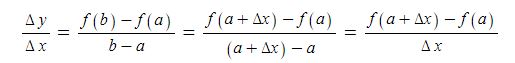
위 식을 x값이 a에서 b로 변할 때의 함수 y=f(x)의 평균변화율이라고 한다.
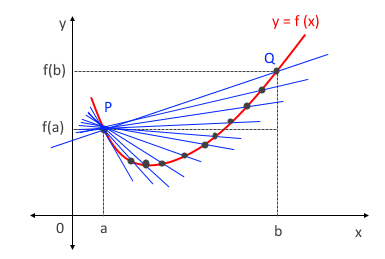
함수 y=f(x)의 평균변화율은 두점 P(a, f(a)), Q (b,f(b))을 지나는 직선의 기울기와 같다.
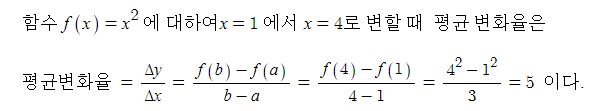
나. 미분계수 (순간변화율)
함수 y=f(x)에서 x의 값이 a 에서 a+△x (=b)까지 변할 때, 평균변화율은 다음과 같다.
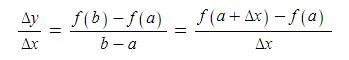
여기서 △x → 0 일 때 평균변화율의 극한값이
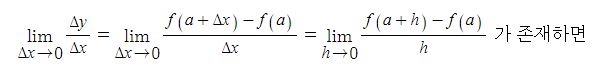
함수 y=f(x)는 x=a에서 미분가능하다고 하고 이 극한값을 함수 y=f(x)의 x=a에서의 순간변화율 또는 미분계수라고 하며
기호로는 f'(a)와 같이 나타내고 f prime a라고 한다. 또한 함수가 어떤 구간에 속하는 모든 x의 값에서 미분가능할 때,
함수 y=f(x)는 그 구간에 서 미분가능하다고 한다. 특히 함수 y=f(x)가 정의역에 속하는 모든 x 의 값에서 미분가능할 때
함수 y=f(x)는 미분가능한 함수라고 한다. 한편, a+△x=x라고 하면 △x=x-a이고 △x →0일 때 x→a 이므로
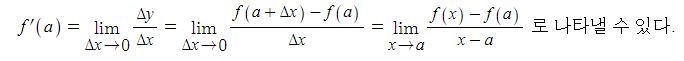
다음 함수는 미분이 가능할까 ?

함수 f(x)=x2 은 x=2에서 미분가능하고 그 때의 미분계수는 f'(2)= 4 이다.
[정리하면]
함수 y = f(x)에 대하여
① x의 값이 a에서 b까지 변할 때의 평균변화율은
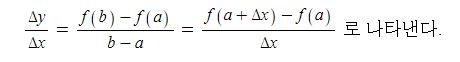
② x = a 에서의 미분계수(순간변화율)은
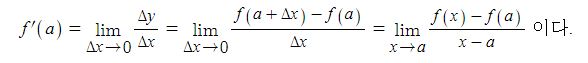
또한 미분계수(순간변화율)은 다음과 같이 나타낼 수도 있다.
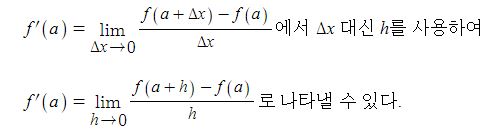
다. 미분계수의 기하학적 의미
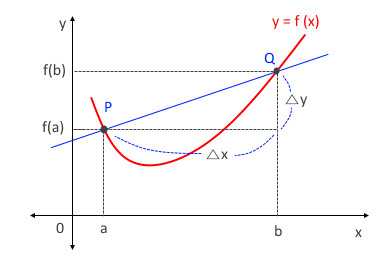
앞에서 x의 값이 a 에서 b까지 변할 때 함수 y=f(x)의 평균변화율
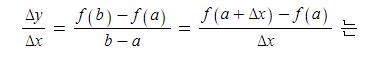
두 점 P(a, f(a)), Q (b, f(b))를 지나는 직선의 기울기와 같다고 하였다.
이 번에는 함수의 그래프에서 미분계수의 기하학적 의미를 알아 보자.
함수 y=f(x)에 대하여 x=a에서의 미분계수 f'(a)가 존재한다고 할 때, b가 a에 한없이 가까워지면 점 Q가 곡선을 따라
점 P에한없이 가까워진다. 역으로 점 Q가 곡선을 따라 점 P에 한없이 가까워지면 b는 a에 한없이 가까워짐을 알 수 있다.
이 때, 직선 PQ는 곡선 y=f(x) 위의 점 P에서의 접선 ℓ에 한없이 가까워지고 점 P는 이 접선의 접점이 된다.
따라서 함수 y=f(x)의 x = a 에서의 미분계수
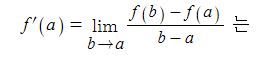
곡선 y=f(x) 위의 점 P(a,f(a))에서의 접선 ℓ의 기울기와 같음을 알 수 있다.
[미분계수 f'(a)의 기하학적 의미
함수 y=f(x)에 대하여 x=a에서의 미분계수 f'(a)는 곡선 y=f(x) 위의 점 (a, f(a)에서의 접선의 기울기와 같다.

점 (a, f(a))에서의 접선이 x축의 양방향과 이루는 각을 θ 라 하면, 미분계수 f'(a)는 다음과 같다. f'(a) = tan θ
[평균변화율과 미분계수의 대소 관계]
평균변화율과 미분계수의 기하학적 의미를 이용하면 그 대소 관계를 알 수 있다.
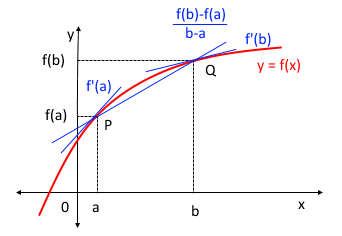
함수 y=f(x)의 그래프가 위 그림과 같을 때, 다음 식의 값의 대소를 비교하여 보자.

다음 함수 y=f(x)의 그래프가 다음 그림과 같을 때

다음 식의 값의 크기를 비교해 보자.
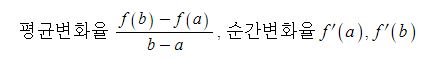
위 그래프는 아래로 볼록한 그래프로 위 식의 크기는 다음과 같다.

2. 미분가능과 연속
앞에서 미분계수의 기하학적 의미는 곡선의 접선의 기울기와 같다고 했다. 그런데 불연속점
에서는 접선을 그릴 수 없으므로 미분이 가능하지 않다는 것을 예상할 수 있다.
그러면 연속인 점에서는 항상 접선을 그릴 수 있어 미분도 가능할까 ? 이에 대한 생각을 하
면서 y = f(x)의 연속과 미분가능 사이에는 어떤 관계가 있는지 알아 보자.
가. 미분가능 : 연속
함수 y = f(x)가 x = a에서 미분가능하면 함수 y=f(x)는 x=a에서 연속이다.
[증명]
함수 f(x)가 x = a 에서 미분가능하면 미분계수
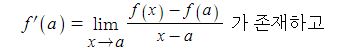
f'(a)는 일정한 값이므로 다음이 성립한다.
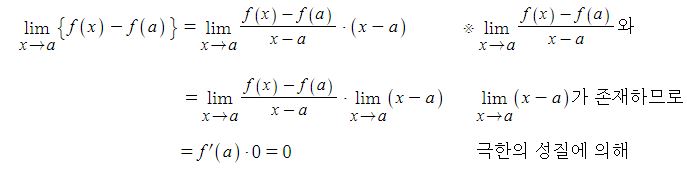
따라서
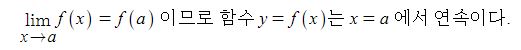
나. 연속 ≠ 미분가능
앞의 명제의 역 '함수 y = f(x)가 x = a 에서 연속이면 y = f(x)는 x = a 에서 미분가능하다'
는 거짓이다. 즉, 함수 y = f(x)가 x = a 에서 연속이지만 y = f(x)는 x = a 에서 미분가능하지 않을 수 있다.
[증명]
함수 f(x) = ㅣx l 를 예로 들어 봅시다.
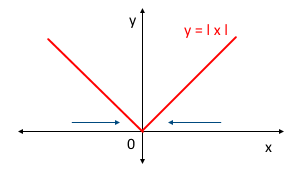
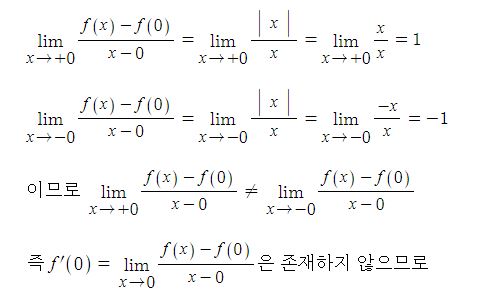
함수 f(x)는 x = 0 에서 미분가능하지 않다. 따라서 함수 f(x) = ㅣxㅣ는 x = 0 에서 연속이지만 미분가능하지는 않습니다.
미분 계수는 함수의 극한으로 정의되어 있다. 함수의 극한에서 좌극한과 우극한이 같은 값에 수렴할 때 함수의 극한이
존재한다고 한다. 즉, 미분계수가 존재하려면 △x → 0 일 때 평균변화율의 좌극한과 우극한이 같아야 한다.
따라서 위와 같은 반례에 의해 함수의 연속성이 함수의 미분가능성을 보장하지는 않는다.
즉, 함수 y = f(x)는 x = a 에서 연속이어도 일반적은로 함수 y = f(x)가 x = a 에서 미분이 가능한 것은 아니다. 또한 위의
함수에서와 같이 x = a 에서 연속이지만 x = a 에서 뽀족하면 (부드럽지 않으면) x = a 에서 미분가능하지 않다.
이러한 점을 뾰족한 점 또는 첨점이라 고 한다.
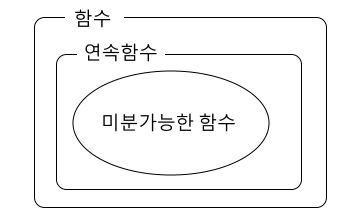
[함수의 미분가능과 연속]
함수 y = f(x)가 x = a 에서 미분가능하면 함수 y = f(x)는 x = a 에서 연속이다.
그러나 그 역은 일반적으로 성립하지 않는다.
[위 명제의 대우]
'함수 y = f(x)가 x = a 에서 연속이 아니면 함수 y = f(x) 는 x = a 에서 미분가능하지 않다' 도 성립한다.
[이차함수 접선의 기울기]
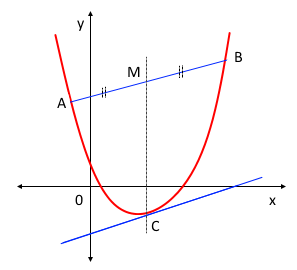
위 그림과 같이 이차함수 즉 포물선 위의 임의의 두점 A, B를 연결하는 직선의 기울기는 점 C (선분 AB의 중점과 x좌표가
같은 점)에서의 접선의 기울기와 같다.
#기울기 #접선 #미분 #연속 #평균변화율 #미분계수 #기하학 #증분 #정의역 #명제 #함수
'전기인이 되는 길 > 전기수학' 카테고리의 다른 글
| 여러가지 함수의 미분법 - 1 (2) | 2023.08.05 |
|---|---|
| 도함수 : 미분방정식 (0) | 2023.08.04 |
| 미분방정식 : 정의, 용어, 개념 (2) | 2023.07.29 |
| 미분방정식 응용 : 뉴턴 냉각법칙, 리비의 탄소연대 추정 (2) | 2023.07.27 |
| 미분방정식 이해하기 (2) | 2023.07.26 |
