두 함수를 몫으로 표현된 함수, 합성함수, 음함수, 역함수, 매개변수로 표현된 함수 등
다양한 형태의 함수의 미분법에 대하여 알아 보자.
1. 몫의 미분법
가. 몫의 미분법

위 함수는 도함수의 정의를 이용하여 다음과 같이 풀이할 수 있다.

위와 같이 매번 도함수의 정의를 이용하여 도함수를 구하는 것은 복잡하고 시간이 많이
걸리게 되는데 몫의 미분법은 결과를 공식화하여 기억하자.

[예제] 몫의 미분법을 이용하여

【 몫의 미분법 】
두 함수 f(x), g(x) (g(x) ≠ 0)가 미분가능할 때

이와 같이 몫의 미분은 결과 공식을 외워 두자.

n이 자연수일 때 다항함수 y = xn 의 도함수가 y' =n xn-1 이다. 그런데 몫의 미분법을 이
용하면 n이 정수일 때도 위 사실이 성립함을 알 수가 있다.

①,②,③에서 알 수 있듯이 n이 양수일 때 뿐만 아니라 0이거나 음의 정수일 때에도 함수
y = xn 의 도함수 y' = n xn-1 이 된다. 즉, 임의의 정수 n에 대하여 y = xn 의 도함수는
y' = n x n-1 이 된다.
【 y = xn 의 도함수 (단, n은 정수) 】

2. 합성함수의 미분법
가. 합성함수의 미분법
함수 y = (2x -3)3 의 도함수를 구하려면 다음과 같이 식을 전개한 후 미분해야 한다.
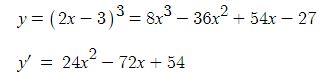
이 처럼 다항함수의 차수가 조금만 높아도 전개한 다음 미분하는 것은 여간 복잡한 것이 아니다.
따라서 함수를 전개하지 않고 미분할 수 있는 방법이 있다면 그 방법을 이용하는 것이 빠르고 계산과정도 간단하다.
합성함수의 도함수가 어떻게 나타나는지를 확인해 보면 그 방법을 구체적으로 확인할 수 있다.
두 함수 y = f(u), u = g(x) 가 미분 가능할 때, 도함수의 정의를 이용하여 합성함수
y =f (g(x))의 도함수를 구해 보자.
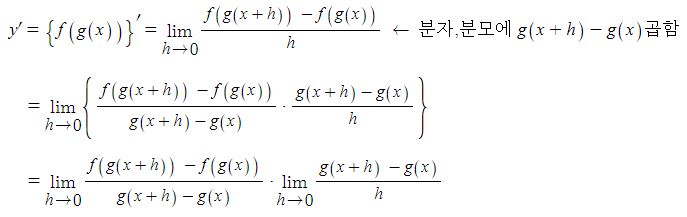
위 식에서 앞, 뒤 두 극한 값을 찾으면 함성합수의 도함수를 구할 수 있다.
① 앞 함수의 극한 값
g(x+h) = B, g(x) = A 라고 하면 함수 y = g(x)미분 가능하므로 연속이다.
따라서 h → 0 일 때, g(x+h) → g(x) 이므로 h → 0 이면 B → A 이다.
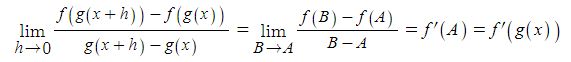
② 뒤 함수의 극한값은 도함수의 정의에 의해 g'(x)가 된다.
따라서 ①, ② 에 의해 합성함수 y = f(g(x))의 도함수는 다음과 같다.
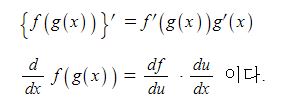
[예제] 함성합수의 미분법을 이용하여 함수 y = (2x-3)3의 도함수를 구해 보자.
이 함수를 f(u)=u3 과 g(x) = 2x-3의 합성합수라고 하면
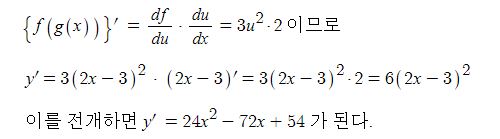
[합성함수의 미분법]

【 합성함수의 미분은 (겉미분) × (속미분)】
합성함수 y = f(g(x))의 도함수를 다음과 같이 기억하자.
① 바깥 쪽 함수 f(x)를 미분하고 안의 함수 g(x)는 그냥 둔 다음 ☜ 겉미분 f'(g(x))
② 안쪽 함수 g(x)를 미분하여 ☜ 속미분 g'(x)
③ 겉미분과 속미분을 곱한다. ☜ f'(g(x)) · g'(x)
위 사실을 적용해 보면
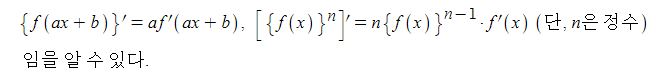
3. 매개변수로 표현된 함수의 미분법
x = t - 1, y = t2 + 1 과 같이 변수 t에 대한 함수 x, y가 주어져 있을 때, 함수 x, y를 각각
t에 대한 한수로 볼 수 있지만 중복되는 변수 t를 소거하여 y를 x에 대한 하나의 함수로 볼
수도 있다. 즉, x = t-1 에서 t = x+1 이므로 이를 y = t2 + 1에 대입하여 변수 t를 소거하면
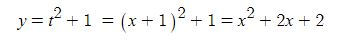
따라서 y는 t에 대한 함수이기도 하지만 x에 대한 함수이기도 하다.
이와 같이 두 변수 x, y의 함수 관계가 변수 t를 매개로 하여 x = f(t), y = g(t)의 꼴로 표현
될 때, 변수 t를 매개변수라 하고 x = f(t), y = g(t)를 매개변수로 표현된 함수라고 한다.
매개변수로 표현된 함수 x = f(t), y = g(t)의 도함수를 구하기 위해서는 매개변수 t를 소거
하여 y = f(x) 꼴의 함수로 고친 다음 미분해야 한다.

함수 x = f(t), y = g(t)가 t에 대하여 미분가능하고 f(t) ≠ 0이면 x=f(t)의 역함수가 존재하고 t는 x의 함수이므로
y = g(t)도 x의 함수로 볼 수 있다.
따라서 t의 증분 △t에 대한 x의 증분을 △x. y의 증분을 △y라 하면 △x→0 일 때 △t→0 이고,
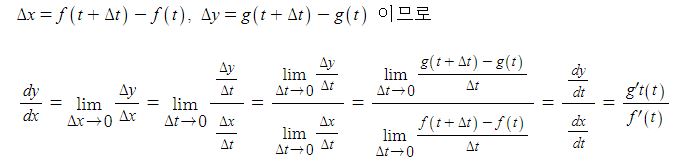
【 매개 변수로 표현된 함수의 미분법】
x = f(t), y = g(t) 가 t에 대하여 미분가능하고 f'(t) ≠ 0 이면
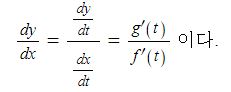
예제 : 매개변수로 표현된 함수의 미분법

4. 음함수의 미분법
가. 음함수의 미분법
일반적으로 함수는 정의역의 원소 x와 공역의 원소 y 사이의 관계식으로 표현할 수 있다.
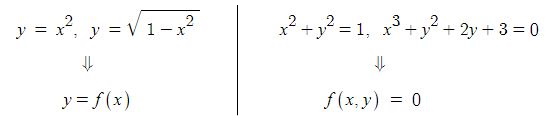
왼쪽과 같이 y = f(x)의 꼴일 때 y를 x의 양함수(Explicit function)라고 하고, 오른쪽과 같이 f(x,y) = 0 의 꼴일 때
y를 x의 음함수 (Implicit function)라고 한다.
음함수 f(x,y) = 0 을 양함수 y = f(x)의 꼴로 고칠 수 있다면 양함수로 변형한 다음 미분하여 도함수를 구할 수 있다.
하지만 음함수 x3+y2+2y+3 = 0 처럼 양함수로 고치기가 어려운 함수들에 대하여 음함수를 양함수 y = f(x)의 꼴로
고치지 않고 바로 미분할 수 있는데 이를 음함수의 미분법이라고 한다.
양함수든 음함수든 미분계수와 도함수는 모두 정의역의 원소인 x의 변화량에 따른 함수값 y의 변화량의 극한을 뜻하는
것이고 이것을 dy/dx라는 기호를 써서 나타낸다. 음함수는 비록 f(x,y) = 0 의 형태를 띠고 있다고는 하지만 y가 x에 대한
함수라고 가정을 한다.
따라서 문자 y를 포함하고 있는 항을 x에 대하여 미분할 때에는 y를 x의 함수로 보고 합성함수의 미분법을 적용하여
미분하는 것이 음함수의 미분법의 핵심이다.
음함수 x2 + y2 = 1 에 위의 사실을 적용해서 양변을 x에 대하여 미분하면

[예제] 음함수의 미분법을 이용하여 x3+y2+2y+3=0 의 도함수를 구해 보자.
양변을 x에 대하여 미분하면

【음함수의 미분법】
x의 함수 y가 음함수 f(x, y) = 0 의 꼴로 주어졌을 때, y를 x의 함수로 보고 각 항을 x에 대하여 미분하여 dy/dx를 구한다.
예제 : 음함수의 미분법을 이용하여 xy = 4 의 도함수 dy/dx를 구하여라.
[풀이] y를 x의 함수로 보고 각 항을 x에 대하여 미분하면
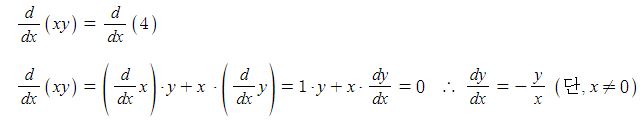
나. y = xr 의 미분법 (단, r은 유리수)
몫의 미분법을 사용하여 n이 정수인 범위에서 (xn)' = nxn-1 이 성립한다는 것을 알았다.
이제 음함수의 미분법을 이용하면 n이 유리수인 범위에서도 성립한다는 것을 알 수 있다.
y = xr (r은 유리수)을 미분해 보자
임의의 유리수 r에 대하여 r = n/m (m,n은 정수, m≠0)으로 나타낼 수 있다.

이 식의 양변을 x에 대하여 미분하면 음함수의 비분법에 의하여
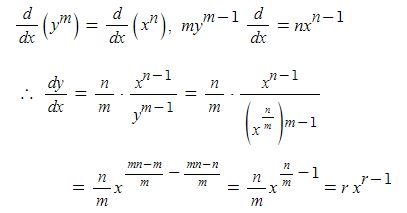
【 y = x^r 의 도함수 (단, r는 유리수】

[예제]

5. 역함수의 미분법
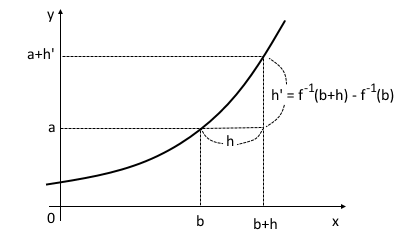
미분가능한 함수 y = f(x)의 역함수 y = f-1 (x)가 존재하고 미분가능할 때 f-1(x)의 도함수를 구해보자.
역함수의 관계에 의해 f(a) = b 이면 f-1(b) = a 이므로 함수 y = f-1 (x)의 x = b 에서의 미분계수를 구한 다음,
이것이 y = f(x)의 x=a 에서의 미분계수와 어떤 관계가 있는지 살펴 보자.
도함수의 정의에 의해 함수 y = f-1(x) 의 x = b에서의 미분계수는

아래 그림과 같이 f-1(b)=a이고 f-1(b+h)=a+h' 이라고 하면 h' → 0 이므로
이를 미분의 정의에 의해 미분을 하면
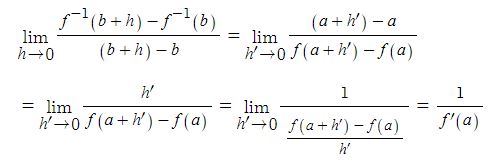
이것을 정리하면 다음과 같이 표현할 수 있다.
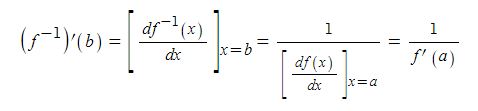
이제 좀 더 범위를 확장하여 앞에서 배운 음함수의 미분을 이용하여 함수와 그 역함수의
도함수 사이의 관계를 확인해 보자.
y = f-1 (x) 라 하면 x = f(y)이고 양변을 x에 대하여 미분하면 좌변과 우변은 각각
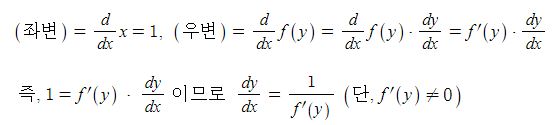
한편, x = f(y) 에서 양변을 y에 대하여 미분하면 dx/dy = f'(y) 이므로 다음이 성립한다.
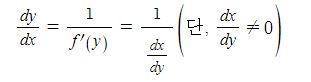
따라서 역함수의 미분법을 이용하면 역함수를 직접 구하지 않고도 역함수의 도함수를 구할 수 있다.
【 역함수의 미분법 】

[예제] 함수 f(x)=x2 (x≥0) 의 역함수를 y=f-1 (x)라 하자. 역함수의 미분법을 이용하여
(f-1)'(4)의 값을 구하여라.
<풀이> f-1 (4) = a 라 하면 f(a) = 4 이므로 a2=4 a=2 ∵ a ≥ 0
역함수의 미분법에 의해
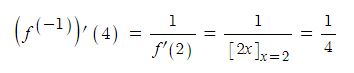
[참고]
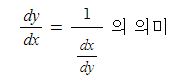
가. 우리가 다루는 대부분의 함수는 일차함수 y = ax+b, 이차함수 y=ax2+bx+c, 지수함수 y= ax, 로그함수 y= log ax,
삼각함수 y = sin x 등의 함수가 모두 양함수로 표현되어 있어야 한다고 생각하기 쉽다. 예를 들어 함수의 표현에
있어서 y5 =2x+1 보다는 y=(2x+1)1/5 이라는 형태에 익숙하고 편안함을 느낀다. 하지만 모든 함수가 항상 양함수
로 표현이 가능한 것은 아니며, 양함수로 표현한다고 하더라도 복잡한 형태를 띠게 되는 경우가 많으므로
dy/dx = 1/dx/dy는 이런 상황에서 큰 역할을 한다.
예를 들어 음함수 y3+y2=3x+2를 y=f(x)로 바꾼 다음에 도함수 dy/dx= f'(x)를 구하는 것은 쉽지 않다.
하지만 양변을 y에 대하여 미분을 하면
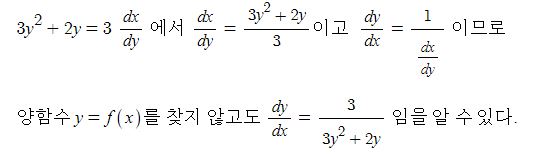
나. 기호 dy/dx 는 독일의 수학자 라이프니츠가 처음 사용한 기호로서 dy를 dx로 나눈 분수가 아니라 그대로 하나의 도함수
를 나타낸다. 하지만 합성함수나 역함수의 미분법에서는 dy/dx를 형식적으로 분수와 같이 다룰수 있는데,
이는 라이프니츠 미분법의 장점이라고 할 수 있다.
앞에서 배운 매개변수로 표현된 함수의 미분법에서도

#몫의미분법 #몫 #도함수 #미분법 #합성함수 #겉미분 #속미분 #매개변수 #함수
#음함수 #양함수 #역함수 #라이프니츠 #로그함수 #삼각함수 #지수함수 #분수
#일차함수 #이차함수
'전기인이 되는 길 > 전기수학' 카테고리의 다른 글
| 여러가지 함수의 미분법 -2 : 미분방정식 (0) | 2023.08.05 |
|---|---|
| 도함수 : 미분방정식 (0) | 2023.08.04 |
| 미분방정식과 미분계수 (1) | 2023.07.30 |
| 미분방정식 : 정의, 용어, 개념 (2) | 2023.07.29 |
| 미분방정식 응용 : 뉴턴 냉각법칙, 리비의 탄소연대 추정 (2) | 2023.07.27 |
비버리님의
글이 좋았다면 응원을 보내주세요!
