1. 라플라스 변환
【 라플라스 변환 정의 】
▣ 시간함수 t로 표현된 미분방정식을 복소변수 S의 대수적 방정식으로 변환시키는 기법
으로 복잡한 파형과 무효성분을 갖는 회로의 정상상태 응답 특성 해석 및 각종 필터설계
에도 활용된다.
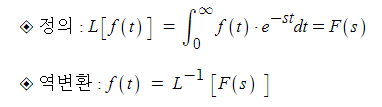
▣ 라플라스 변환을 하는 이유는 복잡한 미분, 적분 방정식을 단순화하기 위함이다.

◈ 하지만 이를 라플라스 변환을 하면 (S-1) / [(S-2) (S-3)] 과 같은 부분분수로 전개하여
쉽게 풀 수 있다.
▣ 다음 식도 마찬가지 이다.

▣ 다음의 미분방정식과 적분방정식이 혼합된 경우에도 마찬가지이다.

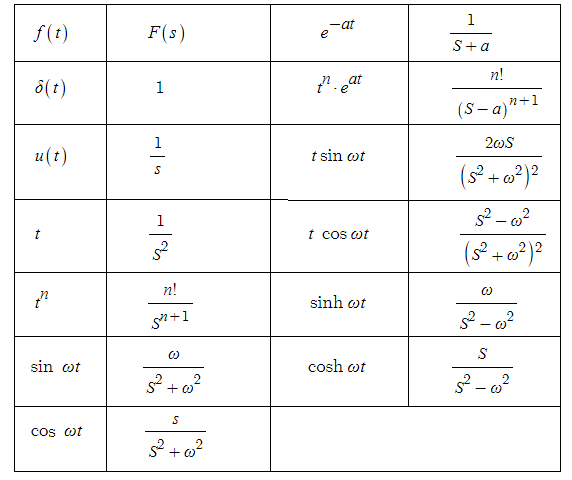
【 주요 라플라스 변환 공식】
가. 단위계단 함수 (Unit Step Function)
▣ 신호에서 "ON" 또는 "OFF"로 되는 함수가 자주 출현한다. 예를 들어 전기회로에 인가
되는 전압은 임의의 시간 후 제거될 수 있는데 다음의 특수한 함수를 활용하면 편리하다.

▣ 특정 신호를 살리려면 x × 1 = x. 제거하려면 x × 0 = 0 하는 함수 이다.
▣ 단위계단함수를 라플라스 변환을 하면 다음과 같다.
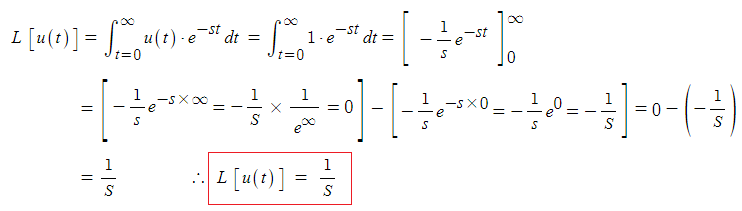
[예제] 2u(t), us(t-2), 2u(t-2)의 그래프를 그려라.

【단위 계단 함수 적용】
▣ 단위 계단 함수는 그래프의 일부를 "Turn Off" 시킨다.
[예제1] u(t) 함수를 이용 y = t·u(t) 함수와 y = t·u(t-2) 함수의 그래프를 그려 보자.

[예제2] f(t) = sin t ·u(t-2π) = ( 0 t < π, sin t t ≥ 2π)의 그래프를 그려 보자.

나. 단위 임펄스 함수 (단위 충격(Impluse) 함수)
▣ 크기, 즉 면적이 "1"인 함수를 말하며 순간적으로 "1"의 크기가 나타났다가 사라지는
파형을 나타내는 함수 이다.
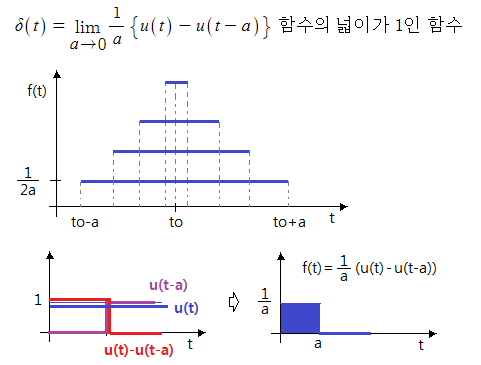
▣ δ(t) 함수의 라플라스 변환 유도식은 다음과 같다.
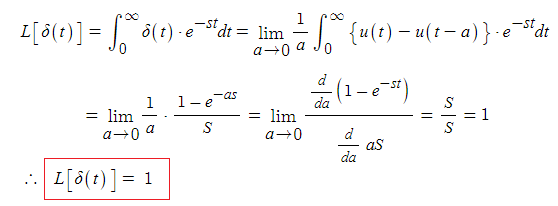
다. 단위 경사함수 (램프함수)
▣ 기울기가 "1" 인 함수이며 t, t · u(t) 로 나타내며 같은 함수이다.
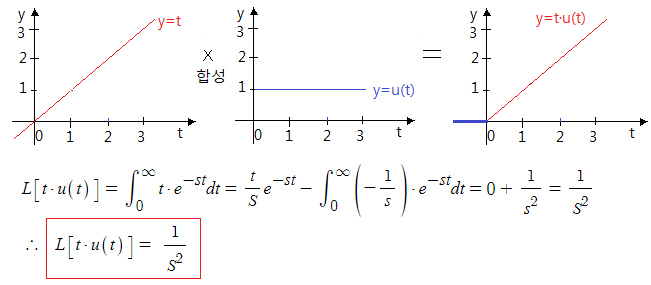
라. 상수 함수 : k , k · u(t)
▣ 상수함수 f(t) = k 는 단위계단함수에 상수를 공급 것과 마찬가지이며 라플라스에서도
상수는 상수 취급을 하여 단위계단함수 1/S 곱하기 상수꼴 즉, k/S 가 된다.
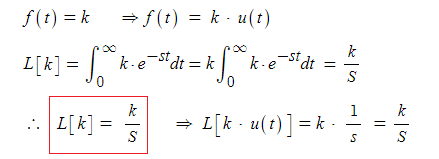
마. 시간함수 : tn
▣ 전기는 시간의 함수인데 시간의 지수함수로 나타낸 방식이다.
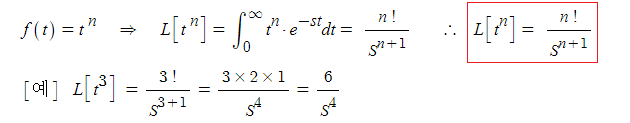
바. 지수함수

사. 삼각함수

아. 쌍곡선 함수
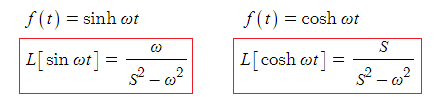
자. 덧셈, 뺄셈 및 실수배 (선형성)
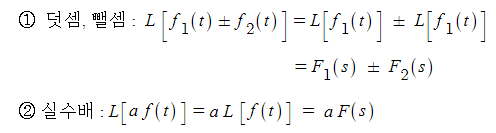
※ 역라플라스 변환에도 위 덧셈, 뺄셈 및 실수배 법칙이 동일하게 적용된다.
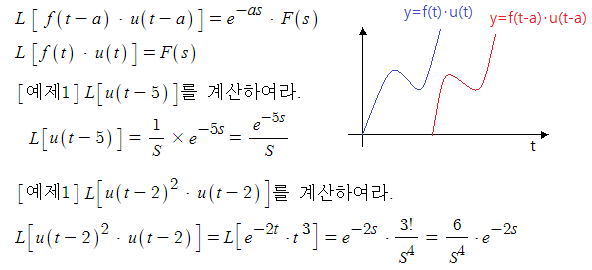
차. 실추이 정리 [이동]
※ 실추이란 함수의 곡선을 이동시키는 것을 말한다.
카. 복소(주파수) 추이 정리
▣ 실수 a에 대하여 e±at 만큼 진폭이 추이된 f(t)의 라플라스 변환
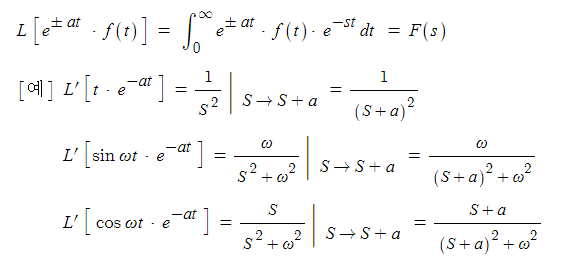
타. 복소미분정리
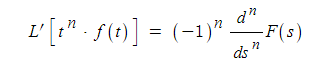
※ L' [tn f(t)] 은 tn은 f(t)를 n번 미분하라.
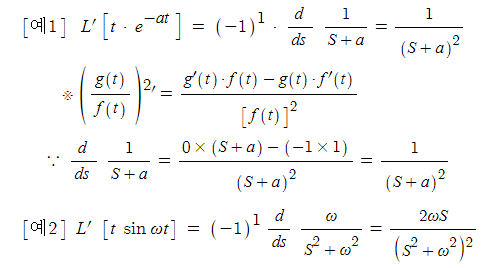
파. 미분정리
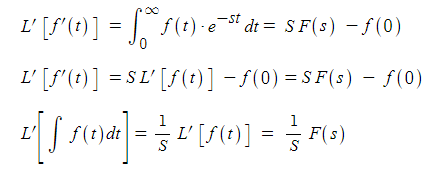
하. 초기값 정리, 최종값 정리
▣ 먼저 초기값에 대하여 알아 보자.

▣ 최종값에 대하여 알아 보자.

2. 라플라스 역변환
▣ 라플라스 S함수를 시간함수 t 함수로 변환하는 것으로 라플라스 변환식을 역으로
적용을 하며 F(s) 함수을 분모를 인수분해하여 부분분수로 변환하여 역변환한다.

▣ 헤비사이드 부분분수식을 이용하여 풀어 보자.
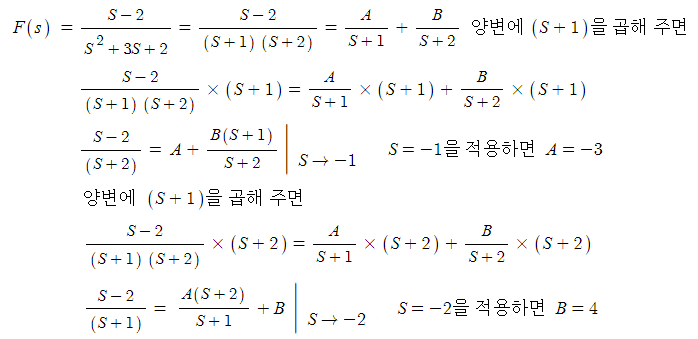
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 전달함수 - 전기 회로 이론 (0) | 2022.01.27 |
|---|---|
| 라플라스 변환 기출문제 풀이 (0) | 2022.01.25 |
| 과도현상 (시정수, 시상수, 특성근) 기출문제 풀이 (0) | 2022.01.23 |
| 과도현상 (시정수, 시상수, 특성근) (1) | 2022.01.23 |
| Z·Y 파라미터, 영상전달함수, 전파정수 기출문제 풀이... (2) | 2022.01.21 |
