미분방정식은 순간변화율을 나타내는 방정식이다. 우리가 일상생활에서 사용하는 속도라른 개념은 거리를 시간으로
미분한 개념이고 가속도는 속도의 변화율을 말하는 것으로 미분의 개념을 포함하고 있다.
수학에서는 도함수를 포함하는 방정식을 미분방정식이라고 한다.
도함수가 몇 차이냐에 관계없이 포함하면 미분방정식이다.
만약 y의 도함수를 포함한다면 미분방정식을 풀어 해를 구한다는 것은 y라는 함수를 구한다는 것이다.

당연한 말이지만 이런 방정식을 구한다는 것은 x를 구한다는 것이다.
그런데 미분방정식에서는 다음과 같이
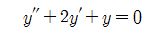
이런 식이 된다. 이는 y"는 y라는 함수를 두번 미분한다는 것이고 y'는 한번 미분한다는
것인데 여기서 y를 구하는 것이 미분방정식을 푸는 미분방정식은 여러가지 형태로 표현을
하는데 미분방정식을 해법은 이들 방정식을 풀이하는 과정이다.
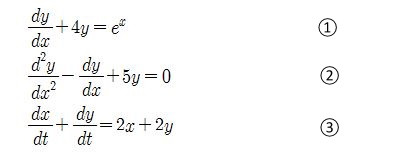
위의 미분방정식은 상미분 방정식이라고 한다. 위 방정식에서는 독립변수가 하나 (①은
독립변수 x, ②는 x, ③은 t)인 경우에 종속변수가 하나 이상인 경우를 상미분 방정식이라
한다. 즉, 하나의 독립변수로 미분을 하는 경우를 상미분이라 한다.
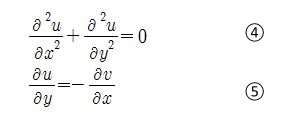
위 의 방정식은 편미분방정식이라고 한다. 독립변수가 2개 이상인 미분방정식을 편미분
방정식이라고 한다. ④, ⑤ 식 모두 독립변수가 x, y 2개 이고 x에 대하여도 미분하고, y에
대하여도 미분을 해야 한다. 편미분에서는 x에 대하여 미분할 때는 y는 상수 취급하고 y에
대하여 미분할 때에는 x를 상수 취급을 한다. 예를 들어 마라톤 선수가 달리기를 할 때 속도
는 바람과 기온의 영향을 받는다고 하면 바람변화에 대한 속도, 기온변화에 대한 속도의
편미분 방정식이 성립하게 되는데 이 때 바람에 대해 미분할 때는 온도는 상수가 되고, 온도
에 대하여 미분할 때는 바람은 상수가 된다. 영어로 표현하면 다음과 같다.
상미분 : Odinary Differential Equation (ODE)
편미분 : Partial Differential Equation (PDE)
도함수는 y', y"로 표현했고 dy/dx로 나타낸다. 이들 두 기호를 모두 사용하는데 4계 도함
수 부터는 다음과 같이 표현한다.
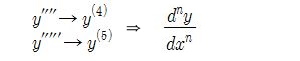
물리학에서는 독립변수로 시간 t를 사용하는 경우가 많은데 이 때 "도트"를 이용하여
도함수를 표현하기도 한다.
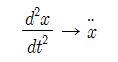
위 식은 x라는 위치를 시간에 따라 두번 미분한다는 의마에서 점을 두개 찍어 나타낸다.
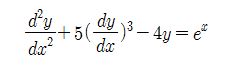
위 식은 2계 1차 미분 방정식이라고 하는데 계는 최고계 도함수의 계수를 의미한다.
최고계는 y를 x에 대하여 2번 미분하는 식이므로 여기서 최고계의 계수 2번 미분 즉 2가
된다. 차수는 최고계 도함수가 몇 제곱함수이냐를 말하는데 위 식에서는 최고계 도함수의
차수가 1제곱 함수이므로 1차 방정식이 된다.
그럼 다음 미분방정식의 도함수는 몇 계, 몇 차 도함수일까 ?
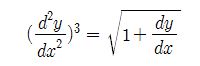
최고계 도함수의 계수가 2차이고 차수가 3이니까 2계 3차 미분방정식이라 할 수 있을까?
우변에 루트식이 있으니 이를 정수식으로 풀어줘서 차수를 결정해야 한다.
따라서 양변을 제곱을 하면 다음과 같이 되겠다.
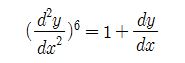
이제 계수와 차수를 말할 수 있겠네요. 2계 6차 미분방정식이 된다. 미분방정식은 표현방법
이 여러가지여서 행태는 다르지만 같은 미분방정식이 되는 경우가 있다. 다음 식을 보자.
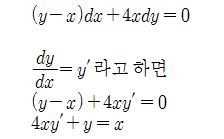
다음은 선형 미분방정식에 대하여 알아 보자
선형미분방정식은 도함수가 1차 선형방정식으로 표현되는 경우이다. 미분, 도함수 즉,
기울기가 직선으로 독립변수와 종속변수간에 비례관계에 있는 경우를 선형 미분방정식
이라 한다. 수치적으로 이야기하면 첫째, 종속변수 y와 모든 도함수 y', y"의 차수가 1차이
고 둘째, y, y', y"의 계수는 독립변수 x에 의존하는 이들 두 조건을 충족해야 한다.
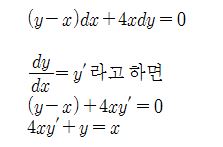
이 미분방정식은 y'의 차수가 1차이고 계수가 4x이므로 x에 의존하는 상황이고 역시 y의
계수가 1 이므로 y에 관계없는 상황이므로 선형미분방정식이 된다.
y" + 2y'+y=0 이라는 미분방정식이 있다면 y"의 차수가 1차이고 계수가 y에 관계없고
y'의 차수도 1차 이고 계수도 -2가 되므로 y에 관계없으며 y도 마찬가지 이므로 선형방정식
이다.

위의 식들은 비선형 미분방정식이다. ①은 y의 계수가 y와 관계가 있고 ②는 y의 계수가
sin(y)이고 ③은 y의 차수가 2차 이므로 비선형 미분방정식이다.
미분방정식의 해는 미분방정식에 그 값을 대입했을 때 방정식이 성립하고 참을 이룬다.
어떤 x에 대한 방정식에서 x=3이 해임을 증명하려면 방정식에 x=3을 대입했을 때 방정식
이 성립하면 그 방정식의 해임을 증명하는 것이다. 미분방정식에서도 마찬가지이다.
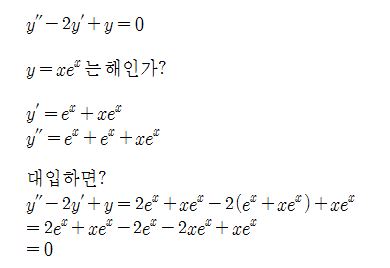
미분방정식의 해가 되려면 그 해는 미분 가능해야 되므로 연속이어야 한다. 미분방정식을
풀고 나면 일반해, 특수해, 즉 General solution과 Particular solution으로 나뉘는데
일반해의 경우 해를 구하고 나서 상수가 남아 있는 경우를 말하고 특수해는 해를 구했을 때
상수가 남아 있지 않는 경우를 말한다.

어떤 미분방정식을 풀어서 해를 구했더니 상수가 들어 있다면 그것은 일반해이고, 문제에서
주어진 초기조건을 대입하여 상수를 찾아서 해를 구했다면 이는 특수해이다. 특히, 물리학이나 공학에서는
특수해를 구하는 것이 중요하다. 예를 들면 어떤 물체가 처음에 정지해 있었다는 초기조건을 쉽게 볼 수 있는데
그런 특수조건을 이용해서 특수해를 구하게 된다.
특히, 미분방정식에서 도함수의 계수와 임의의 상수의 개수가 일치한다. 2계 미분방정식
이면 임의의 상수가 2개가 나와야 하므로 특수해를 구하기 위해서는 초기조건도 2개가 필
요하고 3계면 3개의 상수가 나온다.

이런 경우도 있다. 어떤 미분방정식을 풀었는데 일반해도 구했고 초기조건도 구해서 풀었는
데 잘 살펴보니 y=0도 해가 되는 경우가 있다. 그런데 y=0이라는 해는 일반해의 C에 어떤
값을 넣더라도 나올 수가 없다. 이런 경우 y=0은 일반해도 아니고 특수해도 아닌데 이런 경
우를 '특이해'라고 한다. (Singular solution). 비선형 미분방정식에서는 특이해가 자주
나타난다.
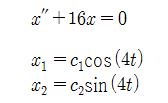
어떤 미분방정식을 풀었는데 2개의 해가 나왔다고 하자. 그런데 앞에서 미분방정식에서
도함수의 계수가 임의의 상수의 개수와 같다고 했다. 이 경우 2계 미분방정식이므로
임의의 상수가 2개가 나와야 하는데 해가 2개이고 임의의 상수가 각각 하나씩 나오기도
한다.

신기하게도 위식에서는 x1과 x2라는 해를 단순히 더해서 하나의 x라는 해를 만들 수
있는데 이 경우도 해는 된다.
x1과 x2 선형결합이 된 x라는 해가 해가 된다는 것이다.
이 경우도 역시 임의의 상수의 개수가 2개이다.

일반적인 경우를 생각해 보면 n계 미분방정식의 특수해를 구하기 위해서는 n계 미분방정식
을 풀어서 나온 일반해에서 임의의 상수의 개수는 n개 이므로 초기조건이 n개 필요하다는
것을 알 수 있다.
이때 초기조건에서 y에 대입하는 x값이 동일해야 한다.
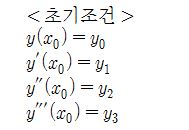
이렇게 미분방정식과 초기조건을 이용해서 미분방정식의 해를 구하는 것을 '초기값 문제
(Initial value problem)이라고 한다. 미분방정식의 계수에 따라서 1개의 초기값 문제,
2계 초기값 문제... 이런 식으로 부른다.
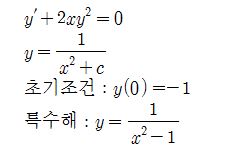
이런 미분방정식을 풀어서 초기조건을 이용해서 특수해를 구했다고 하자.
그런데 특수해 y=1/(x2-1)의 그래프를 그려보면
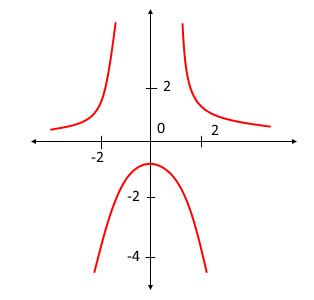
위 그림이 그래프 y=1/(x2-1)라는 함수의 그래프이다. 그런데 문제에서 주어진 초기조건
을 만족하는 부분은 단지
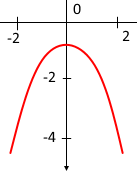
이 부분이 된다. 초기 조건이 y(0)=1 이므로 좌표상 (0, -1)을 지나는 그래프다. '해의 그래프'이다.
'함수의 그래프'이냐 '해의 그래프'이냐의 차이점을 설명하는 부분이다.
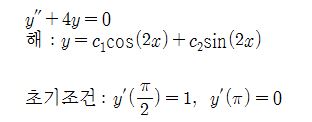
이런 문제가 있는데 위 미분방정식의 일반해가 주어졌고 초기조건이 주어졌다. 그런데
초기조건을 대입하여 풀어보면 C1=0, C1=2 이렇게 나온다. 모순되는 결과이다. 이말은
이 미분방정식의 해가 없다는 뜻이다. 왜 해가 없다고 해야 하는가 ? 앞서 초기 조건에서
같은 x값을 대입하는 것이 중요하다고 했는데 위의 문제에서는 하나는 pi/2를 대입했고
다른 하나는 pi를 대입했기 때문에 이 초기조건만으로는 해를 구할 수 없기 때문이다.
#미분방정식 #미분 #편미분 #일반해 #특수해 #특이해 #독립변수 #종속변수 #도함수
#계수 #차수 #상미분 #선형함수 #비선형함수 #초기조건 #변화율 #기울기
'전기인이 되는 길 > 전기수학' 카테고리의 다른 글
| 도함수 : 미분방정식 (0) | 2023.08.04 |
|---|---|
| 미분방정식과 미분계수 (1) | 2023.07.30 |
| 미분방정식 응용 : 뉴턴 냉각법칙, 리비의 탄소연대 추정 (2) | 2023.07.27 |
| 미분방정식 이해하기 (2) | 2023.07.26 |
| 피벗과 소거법 (Pivots and Elimination method) : 선형 일차 연립방정식 (4) | 2023.02.19 |
