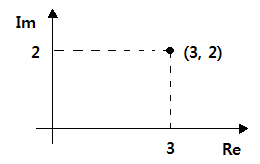
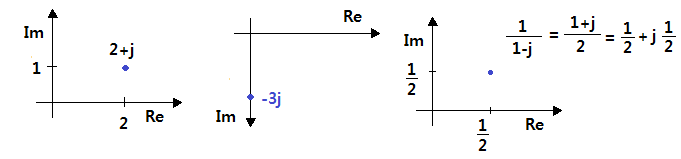
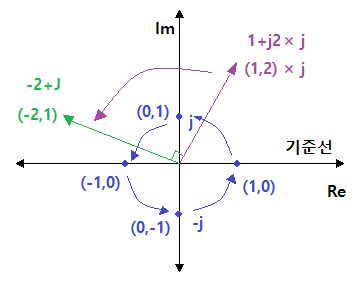
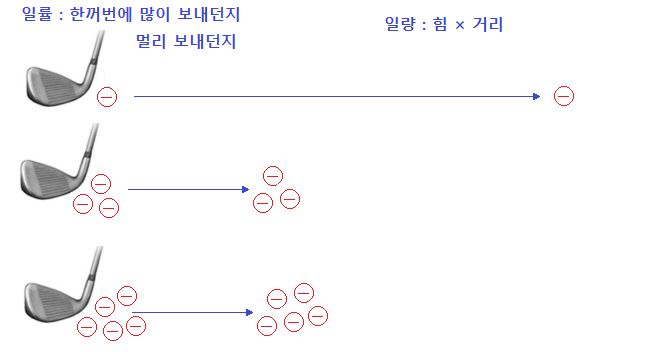
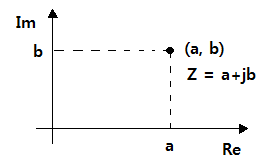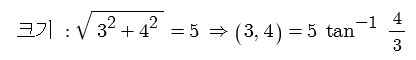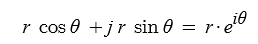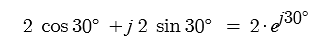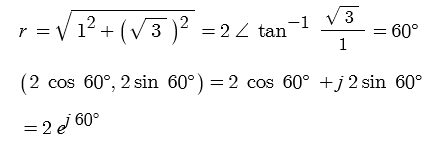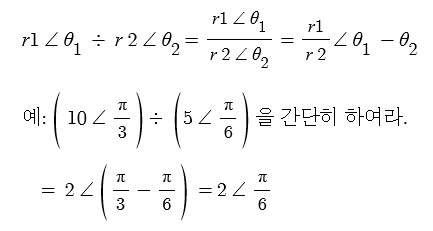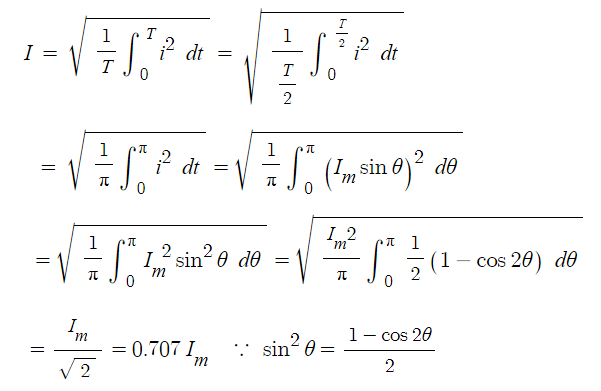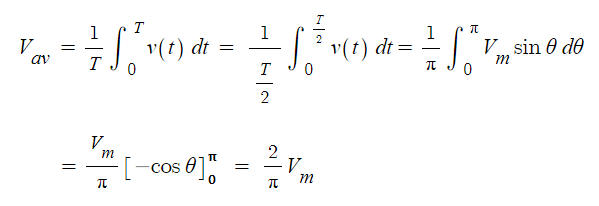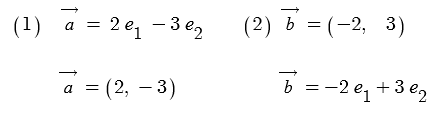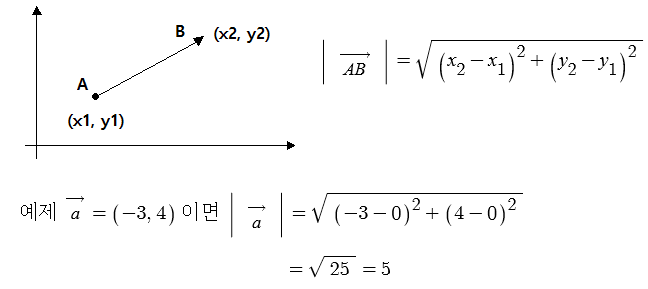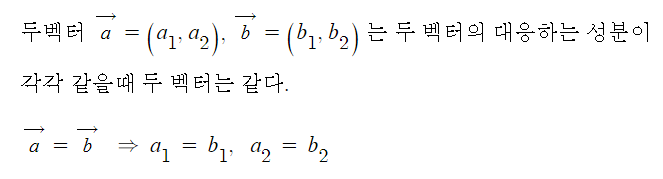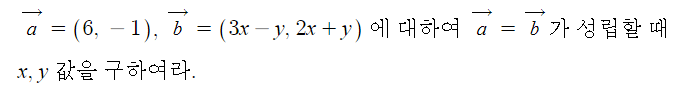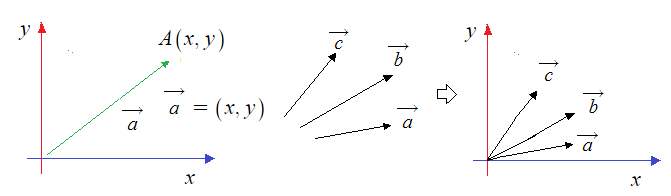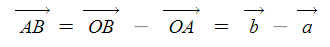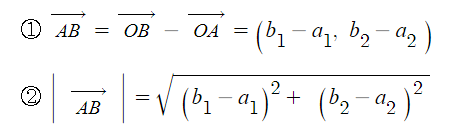1. 정현파 (Sin파) 교류의 발생
가. 전류의 종류
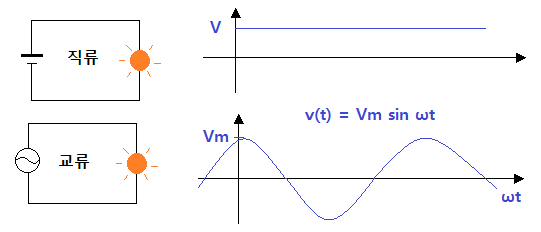
【직류】 D.C (Direct Current) : 전류의 흐름이나 위상이 변하지 않는 것

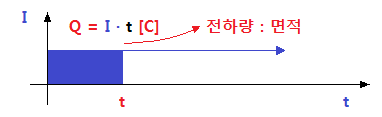
※ 전류의 단위 1[A] : 1초(sec0 동안에 1[C]의 전하가 이동한 전하량을 나타낸다.
▣ 표기 : 영문자 대문자로 표기 V, I
▣ 직류는 시간에 따라 일정한 전하량을 보인다.
【교류】 AC : Alternative Current : 시간에 따라 전하량이 변한다.
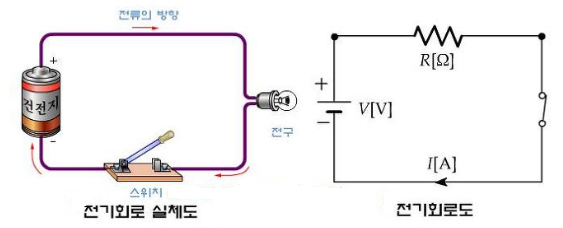
▣ 교류의 표기 : 영문자 소문자 : v, i
▣ 교류 : 시간에 따라 전하량이 변화한다.
가. 사인파의 발생
▣ 우리나라는 60[Hz]를 사용한다.
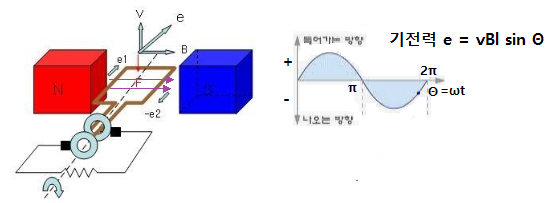
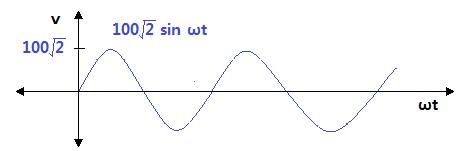
▣ Sin파 형태를 가지며 주기적으로 변화하는 전압 또는 전류
⊙ 유기기전력 e의 크기
e = vBl sin Θ [V]
v : 도체의 회전속도, B : 자속밀도, L : 도체의 길이
Θ : 도체와 자기장이 이루는 각도
▣ 유기기전력은 자기장내에서 도체를 회전시켜 발생시키는데 이를 정류기(슬립링)을
통해 유기기전력을 유인해낸다.
⊙ 이 때 유기기전력의 크기는 도체의 회전속도(v)와 전자석의 자속밀도(B) 및
도체의 길이 (L)에 비례하게 된다. 또한 도체와 자속이 이루는 각도 Θ에
따라에 유기기전력의 크기가 결정된다.
* 유기 기전력 e = vBl sin Θ : 이브 빠에 갔더니 사인해 달라고 하더라
* 회전력 F = BIL sin Θ : FBI 에 갔더니 사인해 달라고 하더라.
▣ 전류 (Current)
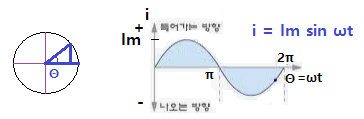
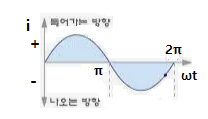
⊙ 도체가 회전함에 따라 파형이 파동이 출렁인다.
※ 자속과 도체가 이루는 각 (Θ)에 따라 기전력의 크기가 결정되는데 도체가 한바퀴
돌면 정현파 (Sin파)의 파형을 이루게 된다.
전류 i = Im sin ωt [A]
▣ 전압 (Voltage)
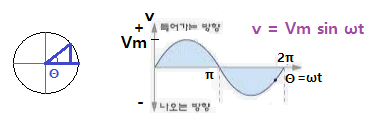
⊙ 전압도 전류와 같은 파형을 나타낸다.
⊙ 주기 (T) : 파형을 한번 반복하는 시간, 시간에 따른 흐름, 1 사이클(Cycle) 시간 [sec]
⊙ 주파수(f) : 1초 동안에 파형 사이클 (Cycle)을 반복한 횟수
f = 60 [Hz] ⇒ T = 1/60 [sec]
※ 주기와 주파수는 반비례, 역수 관계에 있다.
⊙ 각주파수 : ω = 2πf, 기전력의 파형을 기준으로 단위 시간당 회전수
⊙ 각속도 : ω = 2πf
【 호도법 】
▣ 반지름의 길이가 r인 원에서 길이가 r인 호 AB를 정할 때, ∠AOB의 크기(중심각의
크기)를 1 라디안 (radian)이라고 하고 이것을 단위로 하여 각도를 나타내는 방법을
호도법이라 한다.
⊙ 호도법과 육십분법의 관계

※ 호도법 사용 이유 : 각도를 실수화하기 위하여
2. 위상 [Phase]
가. 진상, 지상 파형
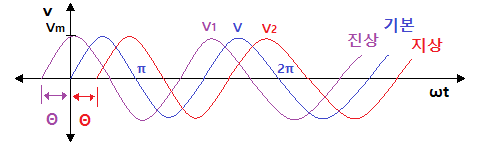
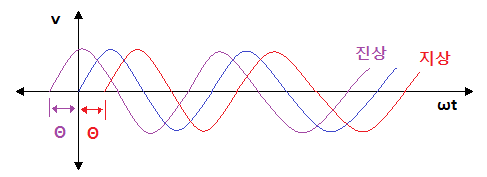
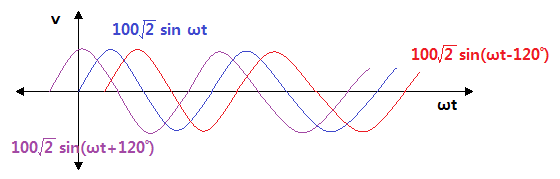
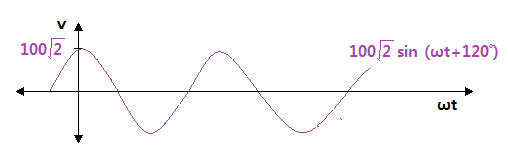
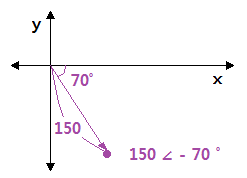
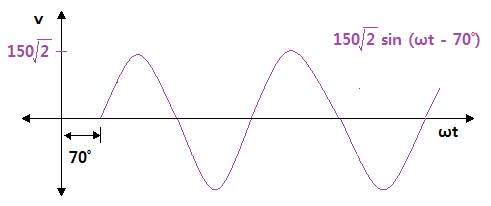
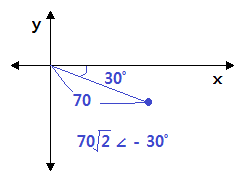
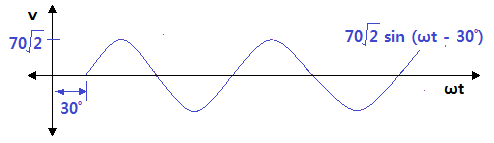
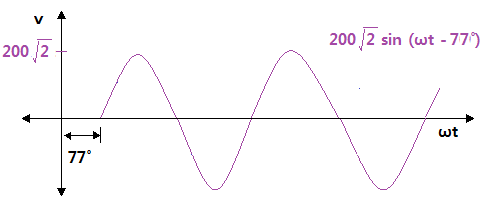
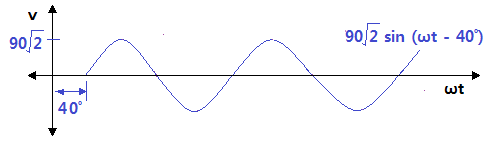
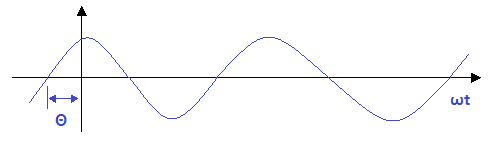
▣ 기본파 보다 위상이 Θ1 만큼 앞선 파형을 진상파형이라 하고 기본파 보다 위상이 Θ2
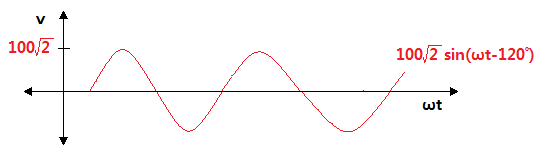
만큼 뒤진 파형을 지상 파형이라고 한다.
주파수가 60[Hz]로 같다는 가정에서 말한다.
⊙ 기본파형 v = Vm sin ωt
⊙ 진상파형 v = Vm sin (ωt + Θ1)
⊙ 지상파형 v = Vm sin (ωt + Θ2)
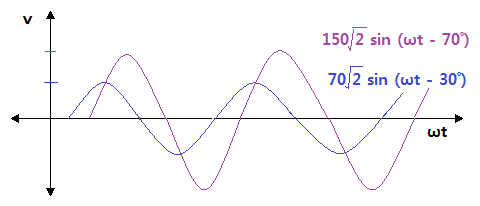
나. 동위상
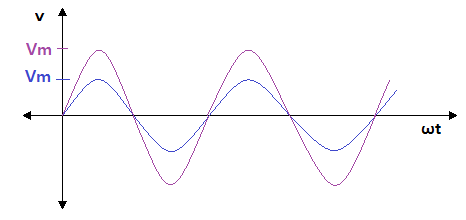
▣ 파형의 크기, 진폭은 다르지만 주기가 같은 파형을 동위상 파형이라고 한다.
이 때도 주파수는 60[Hz]로 같다는 전제에서 말한다.
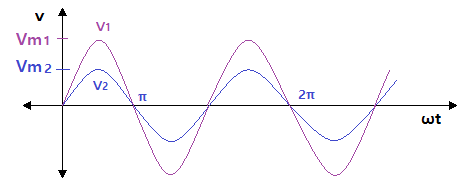
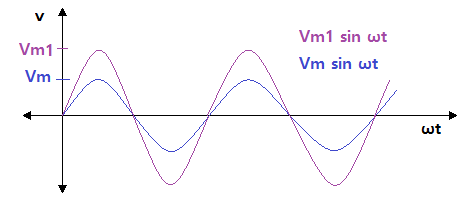
⊙ 진폭이 큰 파형 V1 = Vm sin ωt
⊙ 진폭이 작은 파형 V2 = Vm sin ωt
▣ 위 식에서 보는 바와 같이 동위상이라 함은 파형과 주파수가 같고 진폭만 다른 경우를
말한다. 주파수는 발전소에서 동일하게 유지하므로 동위상이라 함은 파형이 같은 경우
를 말한다.
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| R-L-C 교류회로, R - L 만의 회로 (2) | 2021.12.18 |
|---|---|
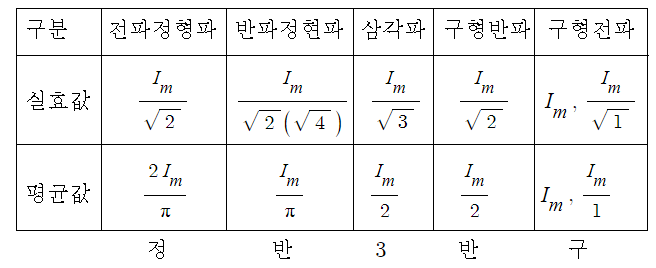
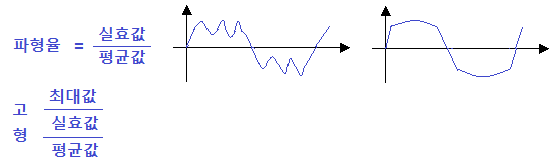
| 정현파(Sin파) 교류의 크기, 파고율, 파형율 (0) | 2021.12.18 |
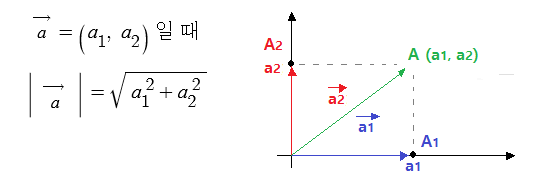
| sin파 (정현파), Sin파는 점이다. 벡터다. (0) | 2021.12.14 |
| 복소평면과 극좌표 - 복소수는 벡터다. (0) | 2021.12.13 |
| 오일러 공식 - 전기수학 (0) | 2021.12.12 |