1. 단위 벡터
▣ 단위 벡터는 크기가 "1"인 벡터를 말한다.
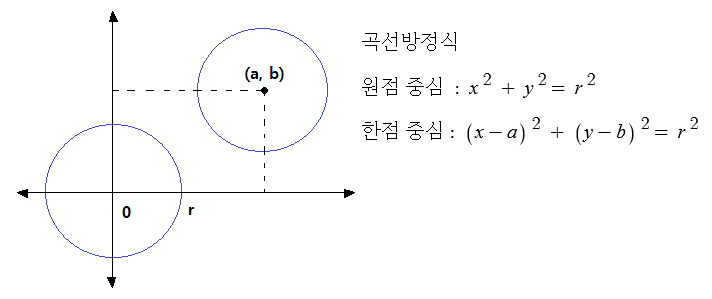
▣ 단위벡터를 좌표평면에 나타내면 다음과 같다.
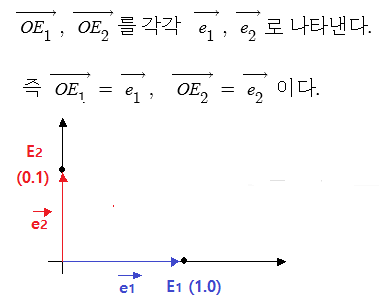
⊙ 좌표 평면 위에서 원점 O를 시점으로 하고
두점 E1 (1,0), E2 (0, 1)를 종점으로 하는 두벡터
2. 평면벡터의 성분 표시
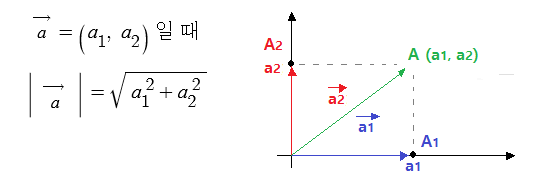
▣ 아래 그림의 평면 벡터 a는
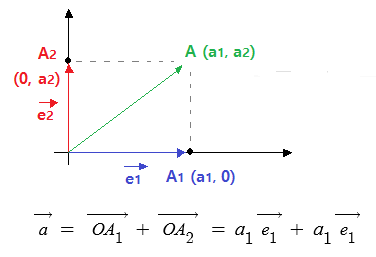
이 때, a1, a2 를 벡터 a의 성분이라 하고 a1, a2 를 각각 벡터 a의 x성분, y성분이라 한다.
벡터 a를 성분을 이용하여 다음과 같이 나타낸다.
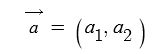
예제 : 다음의 각 평면 벡터를 (1)은 성분으로, (2)는 단위벡터 e1, e2로 나타내어라.
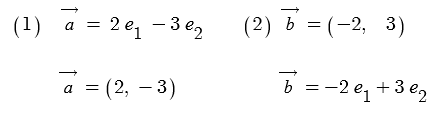
3. 벡터의 크기
※ 두점 사이의 거리
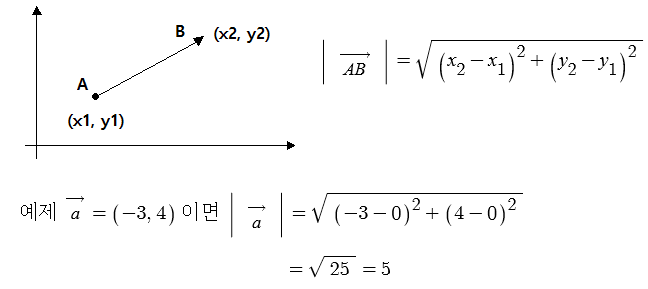
4. 두벡터가 같을 조건
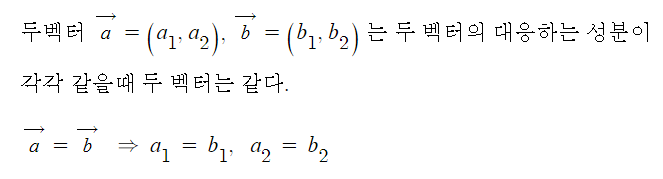
예제1
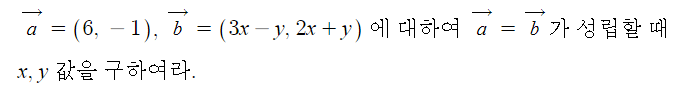
[풀이] 3x - y = 6, 2x + y = -1 ⇒ y = 3x -6, y = -2x - 1
3x - 6 = -2x - 1, x = 1, y = -3
5. 위치 벡터
가. 위치 벡터 정의
▣ 한점 O를 시점으로 하는 벡터 OA를 점 A의 위치 벡터라 한다.
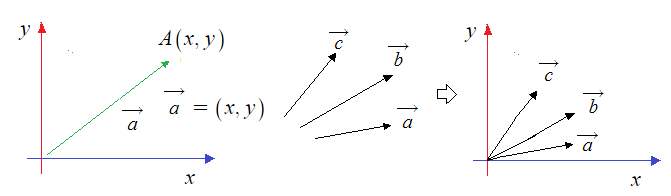
나. 위치 벡터의 성질
▣ 두점 A, B의 위치 벡터를 각각 벡터 a, 벡터 b라고 하면
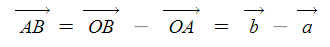
예제 1: 세점 A, B, C의 위치 벡터를 벡터 a, 벡터 b, 벡터 c라고 할 때

예제 2: 세점 A, B, C의 위치 벡터를 벡터 a, 벡터 b, 벡터 c라고 할 때

다. 벡터의 성분에 의한 연산

예제1. 다음 벡터연산을 성분으로 나타내어라.

예제 2. 두점 A(a1, a2), B(b1, b2)에 대하여 벡터의 크기는 ?
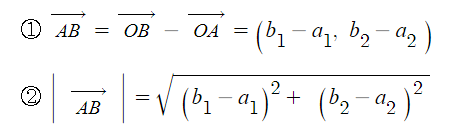
예제 3. 두점 A(3, 3), B(4, 1)에 대하여
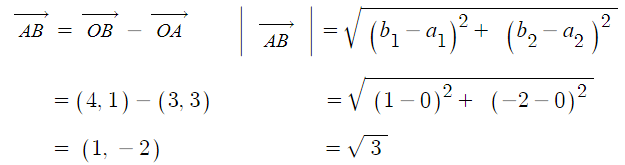
라. 벡터의 평형과 성분
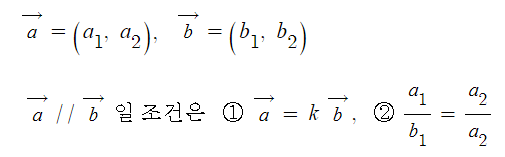
※ 두 벡터가 평행일 조건 : 두 벡터가 실수배 관계
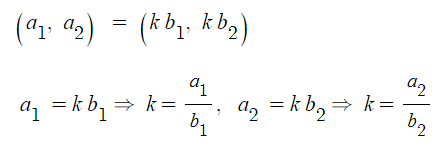
예제1. 좌표평면 위의 두점 A, B가 다음과 같을 때
벡터 AB의 성분과 크기를 각각 구하여라.
가. A (3, 2), B (-5, -1) 나. A (-2, 3), B (4, -1)
[풀이]
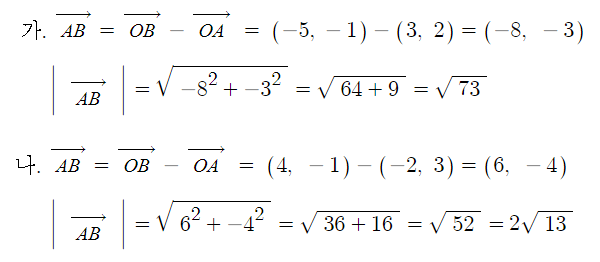
예제 2. 세 벡터 벡터 A = (3, 2), 벡터 B = (-4, 2), 벡터 C = (1, -1) 에 대하여
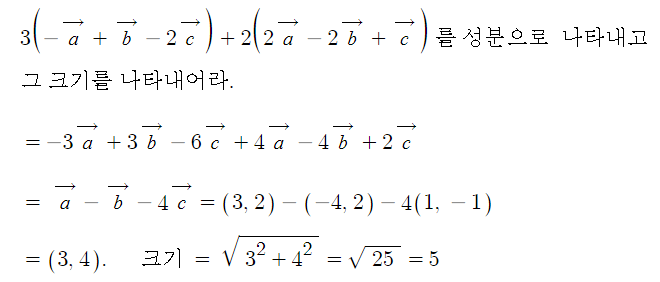
예제 3. 좌표평면위의 세 점 A (3, 2), B (1, -1), C (-2, 0) 에 대하여

'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 오일러 공식 - 전기수학 (0) | 2021.12.12 |
|---|---|
| 정현파 교류의 크기 (0) | 2021.12.11 |
| 기초에서 벡터까지 (0) | 2021.12.09 |
| 전력과 전력량 (0) | 2021.12.05 |
| 전류계, 전압계 접속 (배율기, 분류기) - 회로이론 제5강 (0) | 2021.11.30 |
