1. 기본파
▣ 정현파 교류 전류, 전압은 시간에 따라 사인함수 형태로 변화한다.
⊙ 전압을 기준으로 표현하면 아래 그림과 같다.
v = Vm sinx = Vm sin ωt
▣ v : 각 순간에서의 전압값 (순시값) : 특정 시간 순간 순간 마다 전압값
▣ Vm : 최대값 (진폭)
▣ ω : 각속도 (회전체의 속도 = 회전속도) ω = 2πf
▣ t : 시간
▣ x : x = Θ , Θ = 각속도 × 시간 = ω · t
2. 위상 (Phasor)
▣ 기본파를 기준으로 파형의 앞서는 경우 진상 ( Lead)와 위상이 늦은 경우
지상(Lag)로 나타내는 것
▣ 0˚ 에서 시작한 기본파를 v = Vm sin ωt 라고 한다면
진상의 경우 V1 =Vm sin (ωt + Θ1) 이고
지상의 경우 V2 = Vm sin (ωt - Θ2) 이다.
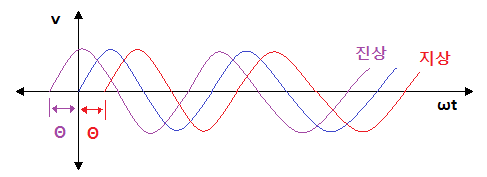
⊙ 진상 : 위상이 Θ 만큼 앞선 파형
v = Vm sin (ωt + Θ)
⊙ 지상 : 위상이 Θ 만큼 뒤진 파형
v = Vm sin (ωt - Θ)
※ 0˚ 에서 시작한 기본파를 V = Vm sin ωt 라고 하면
진상 파형은 V1 = Vm sin (ωt + Θ1) 이고
지상 파형은 V2 = Vm sin (ωt + Θ2) 이다.
3. Sin 파의 최대값
가. 최대값이 변할 때
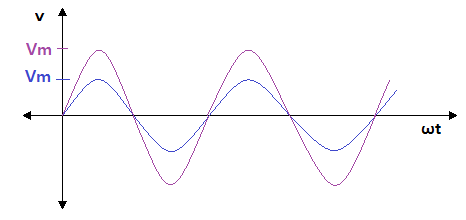
▣ 주파수가 일정하다는 가정하에서 파형도 정현파(Sin파)일 때
두 파형은 위 그림과 같다. 최대값이 다르기 때문에 두 파형은 진폭만 다르다.
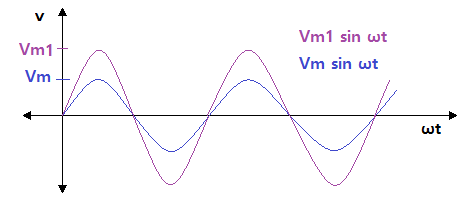
나. 최대값과 위상이 함께 변할 때

▣ 위 그림은 위상과 최대값이 다른 경우를 나타낸다. 주파수가 같고 파형이 정현파
(Sin파)로 같으므로 진폭과 위상이 다르게 된다.
3. 위상 (페이저 (Phasor))
▣ 정현파(Sin파)는 점이다.
▣ 정현파는 벡터이다.
▣ 정현파는 복소수이다.
▣ 정현파는 극좌표이다.
※ 정현파 파형은 같은데 그 위치만 다를 때 위상으로 정현파를 구분하여 표현한다.
⊙ 발전소에서 주파수(60[Hz])를 일정하게 만드므로 위상으로 정현파를 구분한다.
① 3상 정현파 교류의 파형을 나타내 보자.
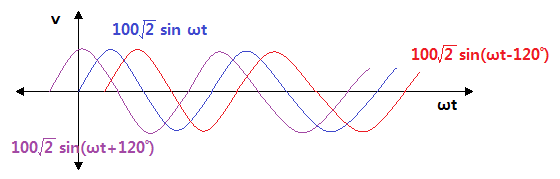
② 기본파형을 그려 보자.
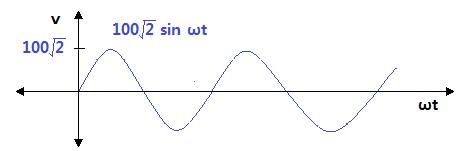
③ 진상파형을 그려 보자.
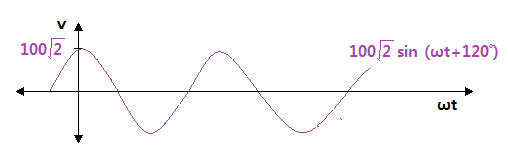
④ 지상파형을 그려 보자.
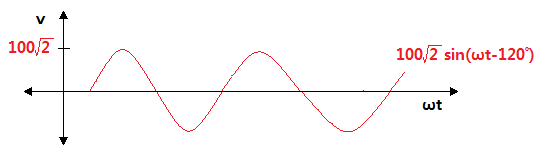
▣ 크기와 위상이 다른 경우의 파형을 그려보자.
⊙ 크기가 다르면 진폭이 다르게 되고 위상이 다르면 순시값의 위치가 다르게 된다.
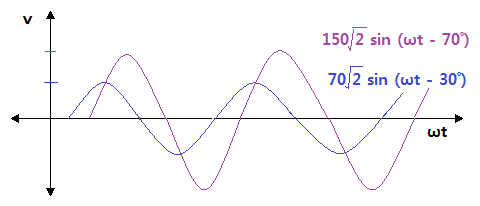
⊙ 150√2 sin (ωt - 70˚) = 150 ∠ -70˚
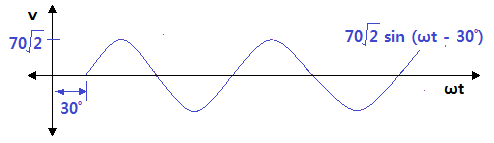
⊙ 70√2 sin (ωt - 30˚) = 70 ∠ -30˚
▣ 한점을 극좌표와 Sin 파형으로 나타내자.
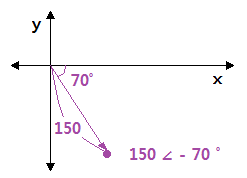
⊙ 극좌표를 정현파형으로 나타내 보자.
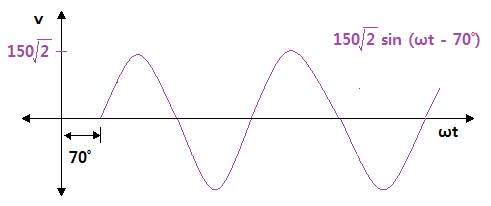
▣ 한점을 극좌표와 Sin 파형으로 나타내자.
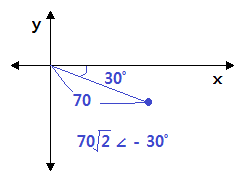
⊙ 극좌표를 정현파형으로 나타내 보자.
▣ 정현파 종족
⊙ 정현파로 파형과 주파수가 같고 크기와 위상이 다른 파형을 정현파 종족으로
통칭한다. 유사한 파형이라는 말이다.
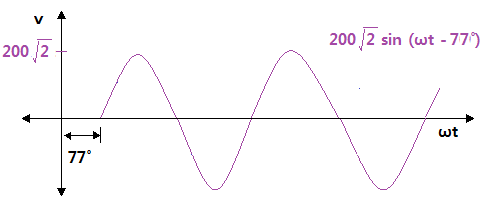
▷ 극좌표 : 200 ∠ -77 ˚
▷ 파형 : 200√2 sin (ωt - 77˚)
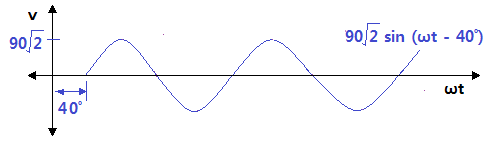
▷ 극좌표 : 90 ∠ -40 ˚
▷ 파형 : 90√2 sin (ωt - 40˚)
【 종합 】
▣ 정현파는 점이다.
▣ 정현파는 벡터다.
▣ 정현파는 복소수다.
▣ 정현파는 극좌표다.
※ Phasor는 위상을 나타내는데 각각의 정현파를 구분하기 위해 사용한다.
【 페이저의 이용 】
1. 주파수가 일정한 Sin파
가. 동일한 각속도를 갖는 여러개의 정현파 또는 미분한 형태의 정현파 도함수 들이
포함되는 경우 그들의 합도 동일한 각속도 ω를 갖는다.
예 : f(t) = cos 2t - √3 sin 2t - 4 sin2t + 4 cos 2t
= 5 cos 2t - (4+√3) sin 2t
= 7.6 cos (2t - 48.8˚)
위 결과와 같이 같은 주파수 ω를 갖는 정현파는 진폭 Vm과 위상 Θ로 특징지을 수 있다.
나. 주파수가 일정한 조건에서 정현파의 파형을 결정하는 2가지 요소는 진폭과 위상이다.
▣ 페이저 : 정현파의 실효값을 크기로 하고 위상을 각으로 하여 하나의 벡터로서 극좌표
형식으로 표현하고, 이를 복소수로 표현한다. 여기서 기준 페이저는 교류에서
위상각이 0˚인 페이저를 말한다.
V를 기준 페이저라 하면

예제 : 다음 순시값을 페이저로 나타내어라.
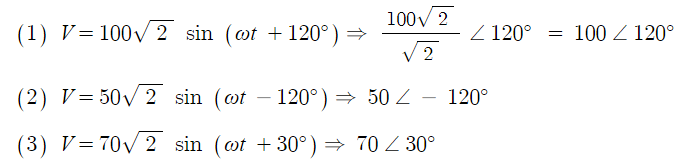
예제 V1 = 20√2 sin ωt [V], V2 = 50√2 sin (ωt+π/3) 일 때 V1 + V2 의 실효값을
구하라.
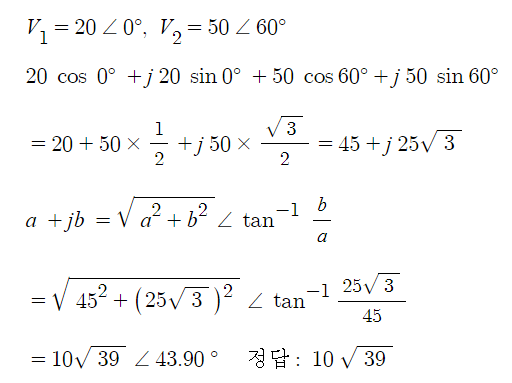
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 정현파(Sin파) 교류의 크기, 파고율, 파형율 (0) | 2021.12.18 |
|---|---|
| 정현파 (Sin파) 교류 (0) | 2021.12.17 |
| 복소평면과 극좌표 - 복소수는 벡터다. (0) | 2021.12.13 |
| 오일러 공식 - 전기수학 (0) | 2021.12.12 |
| 정현파 교류의 크기 (0) | 2021.12.11 |