전력과 전력량

1. 휘스톤브리지

휘스톤브리지

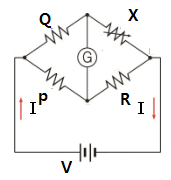
▣ 휘스톤 브리지

 ⊙ G는 검류계로 어떤 때는 전류가 흐르고 어떤 때는 전류가 흐르지 않는다.

     전류가 흐를 때와 흐르지 않을 때의 조건이 있을 것이다. 그 조건을 충족시키기 위해

     저항 X는 가변 저항을 사용하고 있다. 즉 가변 저항을 사용하게 되면 조건을 충족시키는

     저항값을 얻을 수 있다. 이와 같이 저항값을 변경을 통하여 검류계에 전류가 흐르지 않는

     저항을 값을 찾게 된다. 이와 같은 방법으로 검류계에 전류가 흐르지 않는 상태의 저항값은

     마주보고 있는 저항의 곱이 서로 같을 때는 전류가 흐르지 않는데 이 때를 휘스톤 브릿지의

     평형상태라고 하고 이렇게 전류가 흐르지 않을 때의 회로조건을 휘스톤 브리지라고 한다.

 

▣ 휘스톤브리지 평형 조건 : PX = QR

  ⊙ 휘스톤브릿지에서 검류계에 전류가 흐르지 않는 상태를 평형상태라고 하며 이 때의 조건은

      마주보고 있는 저항의 곱의 값이 상호 같을 때 평형상태라고 한다,

  ⊙ 평형조건의 미지의 저항값 : X

      즉 저항값 P × X = Q × X 이다. 이를 X에 대하여 풀어 보면 다음과 같다.  

평형조건

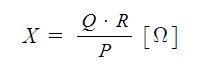
[예제1] 다음과 같은 회로가 주어졌을 때 검류계에 전류가 흐르지 않을 때 

          저항 X의 값을 구하여라.

휘스톤평형

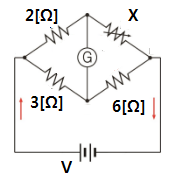
    2 × 6 = 3 × X ⇒ 3x = 12 x = 4 [Ω]

  ▣ 휘스톤 브릿지을 이용하여 가변저항값을 찾는 문제이다.

     휘스톤브리지의 평형조건은 마주보고 있는 저항값을 곱이 서로 같다는 조건이다.

     따라서 마주보는 저항값의 곱 즉 3 x X= 2 × 6 이 된다.

​

[예제2] 다음과 같은 회로가 주어졌을 때 전류 I의 값은 ?

 ※ 검류계에 5[Ω]의 저항을 달았을 때 이 저항에는 전류가 흐르지 않았다.

전류계산

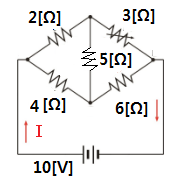
위 그림은 휘스톤 브리지를 나타낸 그림이다. 휘스톤 브리지의 평형상태를 이용하여

전류 I를 구하는 문제를 풀어 보자. 

검류계의 평형조건에서 마주보는 저항의 곱의 값이 서로 같을 때 검류계에 전류가

흐르지 않게 되므로 이를 이용하여 문제를 풀이하게 된다. 검류계 즉 5[Ω]의  저항에 전류가

흐르지 않는 다면 위 회로는 아래와 같이 등가변환할 수 있다. 

 

[위 회로를 등가 변환하면]

휘스톤 등가변환

위 휘스톤브리지 원리에 의하여 검류계에는 전류가 흐르지 않으므로 위 그림 왼쪽과 같이 

회로를 등가변환할 수가 있다. 이를 다시한번 등가변환하면 저항을 직렬연결하면 합성저항은

각각 저항값을 단순합산하면 되므로 5[Ω]과 10[Ω]의 저항이 병렬연결된 회로로 변환할 수 있다.

이는 다시 또 등가변환할 수 있는데 저항의 병렬연결의 합성저항을 구하면 된다. 저항의 병렬연결의

합성저항은 (저항의 곱) / (저항의 합)의 식으로 계산할 수가 있다. 

계산식

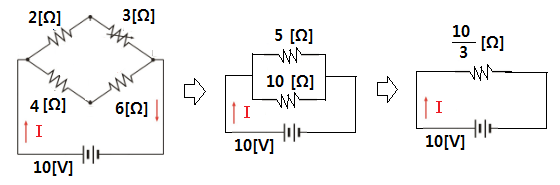
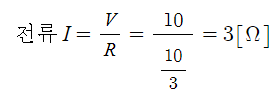
위의 회로를 가장 단순화한 후에는 오옴의 법칙에 의하여 전류값을 구할 수 있다. 오옴의 법칙은

V = IR, I = V/R 의 식을 이용하여 전류값을 구하게 된다.

 

2. 전력과 전력량

가. 전력 (P) : 일률 - 일할 수 있는 능력

□ 전력(P)은 전기가 일할 수 있는 능력을 말한다. 즉 전기가 단위시간당 일할 수 있는 능력을

    말하며, 이는 다른 말로 일률이라고도 할 수 있다. 일이란 힘 × 거리 이므로 단위 시간당

    일을 많이 하려면 힘을 세게 하거나 거리를 많이 이동시키면 된다.

[자동차] 출력(P=W], 마력[P = HP]

출력, 일률

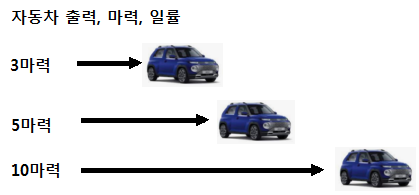
  ▣ 위의 그림은 거리의 개념으로 일률 즉 출력을 나타낸 것이다. 단위 시간당 출력이 높으면

      긴 거리를 갈 수 있도록 함으로서 단위시간당 일량을 많게 할 수 있다. 즉 일률이 3마력은

      단위시간당 3을 갈 수 있고 5마력은 단위시간당 5, 10마력은 단위 시간당 10을 갈 수가

      있다. 이와 같이 출력(일률)이 높으면 동일한 시간에 많은 일을 할 수 있게 된다. 

 

나. 전력량 (W) : 일량 - 전력이 한 일의 양

 

일률과 일량

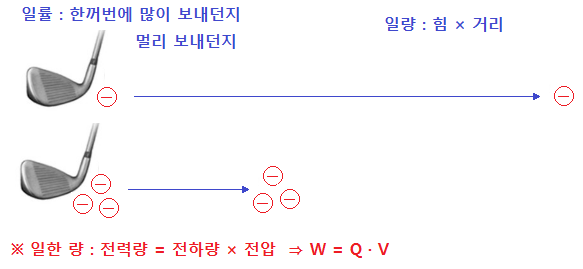
 위 그림은 일량을 골프로 비유하여 나타낸 것이다. 골프채로 전하량을 이동시키기는 것을 일이라고

 한다면 적은 수의 전하를 먼거리로 보낸 것과 많은 수의 전하량을 작은 거리를 이동시킨 것은

 일량이 같다고 할 수 있다.

 

다. 종합

▣ 종합하여 보면 전기가 하는 일률인 전력과 전기가 한 일의 양인 전력량은 다음과 같이 

    정리할 수 있다.

전력, 전력량

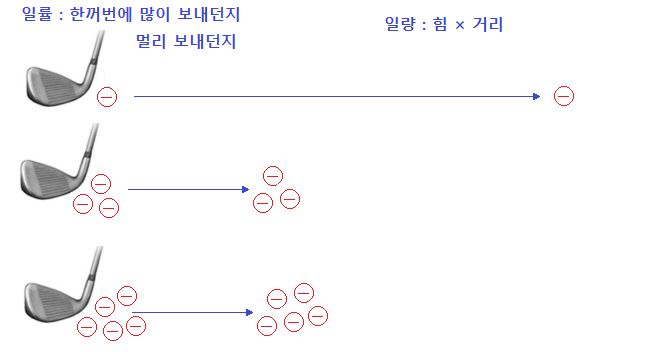
   위 그림에서 일률 즉 전력은 한번에 얼마나 많은 전하량을 보낼 수 있는가와 관련이 있고

   일량인 전력량은 얼마나 많은 전하량을 얼마 만큼의 거리를 이동시켰는가와 관련이 있다.

   따라서 일률인 전력과 일량인 전력량은 다음과 같이 요약할 수 있다.

 

   일률, 전력 P = 일 ÷ 시간 = 전력량 ÷ 시간 = (전하량 × 전압) ÷ 시간

   전력량 W = 전력(P) × 시간 (t) W = P · t ⇒ P = W/t ⇒ P = (Q · V) / t

​

▣ 전력 : 단위시간 동안에 전기가 한 일의 양 (능력)

             P = V · I = I2·R = V2/R = W/t [W] = [J/sec]

             1[HP] =746 [W] ⇒ 1[HP] : 말 7마리를 사육했다.

▣ 전력량 : 임의의 시간동안 전기가 한 일의 양 (에너지)

                W = Pt = VI · t = I2R · t = V2/R · t [J] = [W·sec]

                1[J] = 0.24[cal] ⇒ 주울의 법칙

                1[Wh] = 3600 [J]