1. 복소수의 기하학적 표현
▣ 벡터, 복소수, 지수함수는 같은 것을 다르게 표현한 것이다.
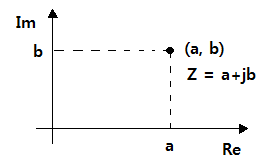
▣ 전기에서 사용할 j를 본격적으로 사용해 보자
전기에서는 보통 교류 전류를 i를 써서 표현하므로 그와 구분하기 위해 i대신에
j를 사용한다.
▣ 벡터를 좌표값으로 표현하기 위해 복소수로 좌표평면에 표시할 수 있게 된다.
따라서 좌표평면이 벡터와 복소수를 연결해 준다.
▣ 복소평면에서 Z = a+bi = a +jb로 나타내자.
이를 가로축을 실수축, 세로축을 허수축으로 하여 각각 실수부와 허수부의 수를
(a, b) 좌표로 표시한다.
예) 3+2i = 3+j2으로 나타낸다. 또한 복소 평면위에 (3, 2)의 점으로 표시한다.
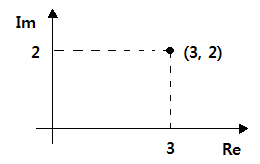
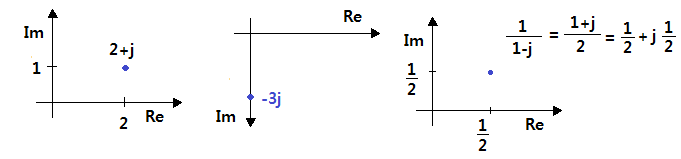
예 2) 다음 복소수를 복소평면에 표시하여라.
(1) 2 + j (2) -j3 (3) 1/(1-j)
2. 허수 j의 이용
▣ 허수 j를 이용하면 복소수체계를 이용하여 벡터를 표현하고 수의 회전을 포함한 성분의
회전을 표현할 수 있다.
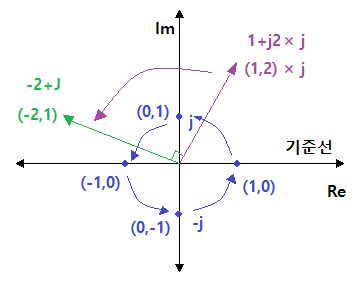
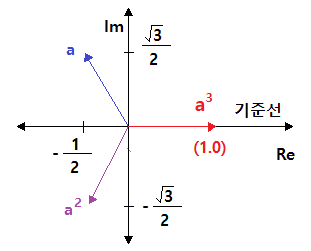
① 1 × j = j : j를 곱하는 순간 90˚ 좌회전한다.
② j × j = -1 : j를 곱하는 순간 90˚ 좌회전한다.
③ -1 × j =- j : j를 곱하는 순간 90˚ 좌회전한다.
④ -j × j = 1 : j를 곱하는 순간 90˚ 좌회전한다.
※ 벡터의 회전을 아주 편리하게 회전시키는 개념이 복소수에 있다.
예 : 벡터 (2,3)을 복소수를 이용하여 2+ㅓ3으로 나타낼 수 있다. 이 때 2+j3에 j를 곱하
면 즉, (2+j3) × j = -3 + 2j 가 되어서 복소평면에서 벡터의 회전을 표현할 수 있다.
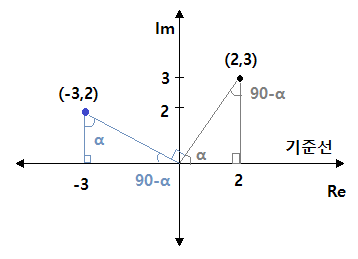
예 : 3상 교류에서 벡터 연산자의 회전을 알아 보자

3. 극좌표
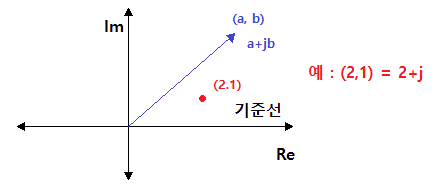
가. 직교좌표
▣ 가로축을 x축, 세로축을 y축으로 하여 평면을 나타내는 좌표, 이 때 직교좌표 (x, y)를
복소수 x+jy로 나타낼 수 있다.
나. 극좌표
▣ 원점에서 그 점까지의 거리와 x축과 이루는 각도로 나타내는 좌표
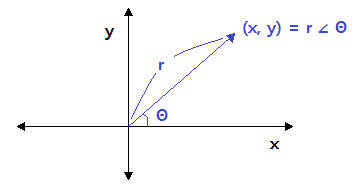
▣ (x, y) = r ∠ Θ 로 나타낸다.
예 : ( √3, 1) = 2 ∠ 30˚
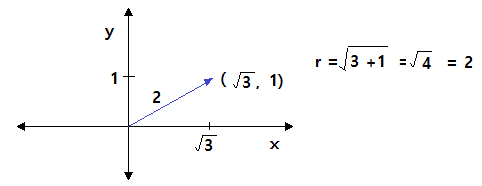
다. 극좌표와 직교좌표의 변환
① 극좌표 r ∠Θ 를 직교좌표 (rcosΘ, rsinΘ)로 변환하여라.
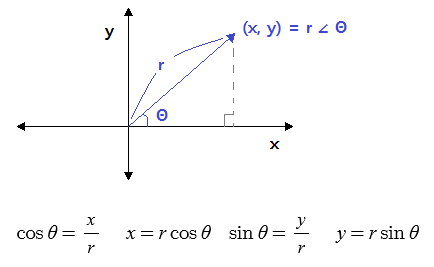
ex : 2 ∠30˚ 를 직교좌표로 바꾸면 ?
= (rcosΘ, rsinΘ) = (2cos 30˚, 2sin30˚) =(2×√3/2, 2 × 1/2)
= (√3, 1)
② 극좌표 r ∠Θ 를 복소수 형태로 변환하면 ? rcosΘ + j sinΘ 로 나타낼 수 있다.
③ 지수함수의 표현
▣ 오일러의 공식을 이용하여 복소수를 지수함수로 변환할 수 있다.
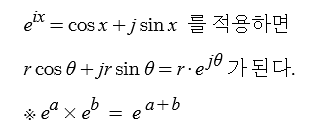
④ 직교좌표 (x, y) - x + jy 의 극좌표 표현
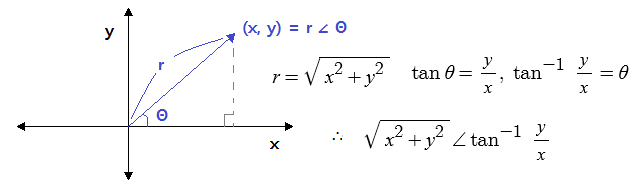
예제. 좌표 (3,4)를 극좌표로 표현하면 ?
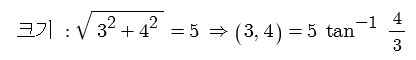
▣ r ∠Θ = (rcosΘ, rsinΘ) = (x, y)
(x, y) = x + jy = rcosΘ + j rsinΘ
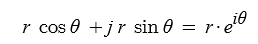
예제 : 2∠30˚ = (2 cos 30˚ , 2 sin 30˚) = (√3, 1)
(√3, 1) = √3 + j = 2 ∠tan-1 1/√3 = 2 cos30˚ + j 2 sin30˚
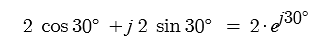
예제 : 극좌표 2 ∠ 60˚ 를 직교좌표로 바꾸어라.
(2 cos 60˚, 2 sin 60˚) = (2 × 1/2, 2 × √3/2) = ( 1, √3)
예제 : 직교좌표 (1, √3)을 복소수로 나타내어라. 1+j√3
예제 : 직교좌표 (1, √3)을 삼각함수로 표현하여라.
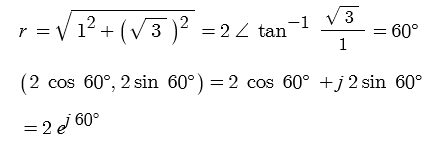
예제 : 직교좌표 (1, √3)을 지수함수로 표현하라.
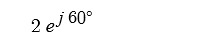
예제 : 극좌표 2 ∠ 30˚ 를 직교좌표로 표현하라.
= (2 cos 30˚, 2 sin 30˚ ) = (2 × √3/2, 2 × 1/2) = (√3, 1)
예제 : 직교좌표 (√3, 1) 을 삼각함수로 표현하라.
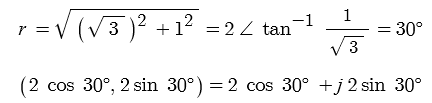
예제 : 직교좌표 (√3, 1) 을 지수함수로 표현하라.

4. 극좌표의 연산
가. 덧셈 : 복소수로 변환하여 계산한다.
r ∠ Θ = r cos Θ + j sin Θ
예 : 3 ∠ 30 ˚ + 2 ∠ 60 ˚ = (3cos 30˚ + j 3sin30˚)+(2 cos 60˚ + j 2sin60˚)
= (3√3/2 + j 3/2) + (2/2 + j 2√3/2) = (2+3√3)/2 + j (3+2√3)/2
= 4.84 ∠ 41.93
나. 뺄셈 : 복소수로 변환하여 계산한다.
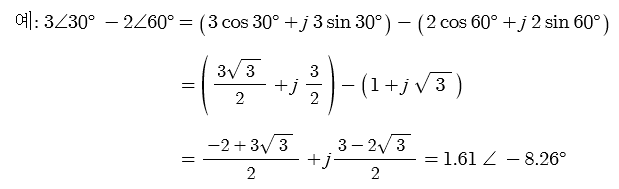
다. 곱셈
▣ (r1 ∠ Θ1) × (r2 ∠ Θ2) = r1 × r2 ∠ Θ1 + Θ2
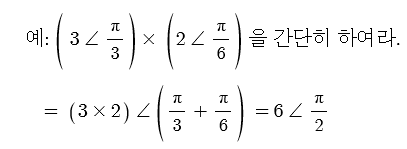
라. 나눗셈
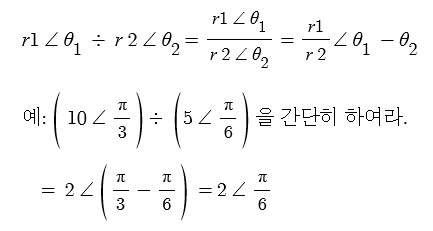
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 정현파 (Sin파) 교류 (0) | 2021.12.17 |
|---|---|
| sin파 (정현파), Sin파는 점이다. 벡터다. (0) | 2021.12.14 |
| 오일러 공식 - 전기수학 (0) | 2021.12.12 |
| 정현파 교류의 크기 (0) | 2021.12.11 |
| 기초에서 벡터까지.. 벡터 성분 - 전기수학 (0) | 2021.12.10 |
