【키르히호프의 법칙 】
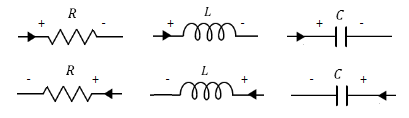
▣ 능동소자 (Positive)
⊙ 스스로 어떤 전기적 작용을 일으키는 소자를 말한다.
⊙ 능동소자에는 전압원, 전류원 등이 있다.
※ 능동소자는 기전력을 발생시키거나 전류를 발생시키는 장치를 생각하면 된다.
전기장치로서는 발전기, 건전지 등의 기기를 생각하면 된다.

▣ 수동소자 (Passive)
⊙ 스스로는 전기적 작용을 일으키지 못하고 다른 에너지를 받아 전기적 작용을
일으키는 소자를 말한다.
⊙ 수동소자에는 저항, 리액터, 콘덴서 등이 있다.
⊙ 수동소자는 스스로는 아무 것도 못하고 능동소자와 연결될 때 비로소 전기적 작용을
할 수 있다.
※ 일반적인 전기소자는 대부분 수동소자라고 보면 된다. 장기장치를 구성하는 소자는
저항, 리액터, 콘덴서로 구성되어 있기 때문에 일반적으로 소자하면 수동소자를 떠올린다.
1. KCL 제1법칙 (전류법칙)
▣ 임의의 점에 들어 온 전류와 나간 전류의 대수 합은 "0"이다.
⊙ 전기에서 중요한 것이 전류이므로 KCL 제1법칙은 전류법칙이다.
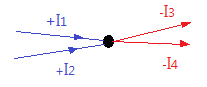
I1 + I2 - I3 - I4 = 0
한 점에 들어오는 전류와 한점에서 나가는 전류의 합을 같다.
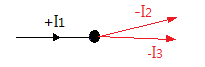
I1 - I2 - I3 = 0, I1 = I2 + I3
한 점에서 들어 오는 전류의 합과 나가는 전류의 합은 같으므로
한점에 들어 오는 전류는 하나이고 유출되는 전류는 두개 이므로
유출되는 전류 2개의 값의 합은 유입 전류와 같게 된다.
2. KVL 제2법칙 [ 전압법칙 ]
▣ 루프를 형성하는 회로망에서 모든 기전력의 대수합은 전압강하의 대수합과 같다.
⊙ 하나의 폐회로 내에서 전압상승분의 합과 전압강하분의 합의 같게 된다.
또한 전압원만을 연결한 경우에는 각각의 전압원의 극성을 고려한 전압상승순의 합과 전압
강하분의 합의 같게 된다.
⊙ 전압강하 = 전압상승 ∑ V = 0
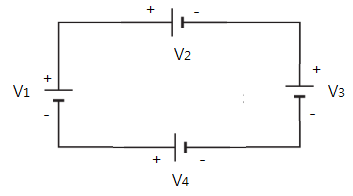
▣ V1 을 기준으로 할 때 : V1 을 기준으로 각 기전력의 극성을 비교하여 산정한다.
V1 - V2 - V3 + V4 = 0
V1 + V4 = V2 + V3
⊙ V1을 기준으로 할 때 극성이 같은 것은 전압읠 더해주고 극성이 다른 경우에는
전압을 빼주어 합성 전압으로 "0"이 된다.
▣ V2 을 기준으로 할 때 : V2 을 기준으로 각 기전력의 극성을 비교하여 산정한다.
V2 + V3 - V4 - V1 = 0
V2 + V3 = V4 + V1
⊙ V2을 기준으로 할 때 극성이 같은 것은 전압읠 더해주고 극성이 다른 경우에는
전압을 빼주어 합성 전압으로 "0"이 된다.
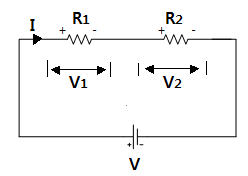
▣ 전압상승분의 대수합과 전압강하분의 대수합은 같게 된다.
V - V1 - V2 = 0
V = V1 + V2
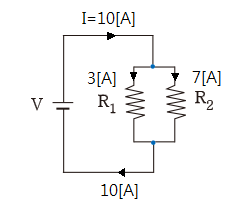
예제 1. 아래 회로에서 R1에 흐르는 전류는 몇 [A]인가 ?
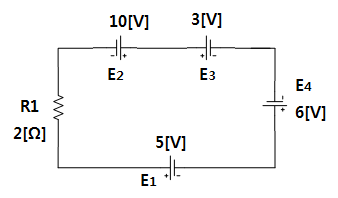
▣ 전압상승분의 대수합과 전압강하분의 대수합은 같다.
⊙ 전압상승분(기전력)의 대수합을 먼저 구하면
E1 + E2 + E3 + E4 = 10 + 5 -3 + 6 = 18 [V]
⊙ 전압상승분 = 전압강하분 이므로 VR1 = 18 [V]
※ 먼저 전체 전압원에 대한 전압상승분을 계산하게 된다. 전체 전압상승분은
극성을 고려하여 극성이 같은 것은 더해주고 극성이 다른 것은 빼 주어
합성전압을 구하게 된다.
▣ 전류 I = 전압 [V] ÷ 저항 [R]
I = 18 ÷ 2 = 9 [A]
※ 합성저항을 구한 다음에는 전류를 구하기 위해서는 오옴법칙을 이용하여
전류를 구하게 된다.
예제 1. 아래 회로에서 R1,R2,R3,R4 에 걸리는 전압은 각각 몇 [V] 인가 ?
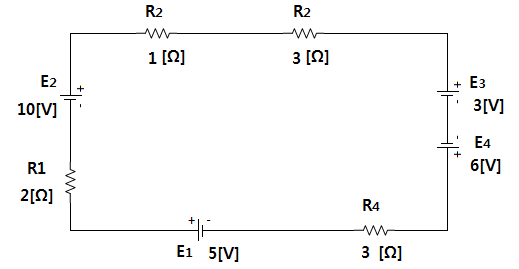
▣ 전압상승분(기전력)의 대수의 합과 전압강하분의 대수의 합은 같다.
⊙ 기전력의 합 = E1 + E2 + E3 + E4 = 5 + 10 - 3 + 6 = 18 [V]
∴ 전압강하분 전체 전압의 대수의 합은 18[V]이다.
⊙ 그런데 전압 V = I · R 이고 직렬회로에서 전류 I는 일정하므로
전압은 저항 R에 비례하게 된다.
전체 전압을 구했으면 오옴의 법칙을 이용하여 저항에 걸리는 전압을 구한다.
오옴의 법칙을 적용하기 위해서는 전류를 구해야 하는데 직렬회로에서는
각각의 저항에 흐르는 전류는 일정하다. 따라서 전체 전류는 전압/합성저항
으로 구할 수 있다. 즉 합성저항은 18/9 = 2[A]이다.
이제 각각의 저항에 걸리는 전압은 V=IR에 의하여 계산할 수 있다.
따라서 각각의 저항에 걸리는 전압은 R1= 4[V], R2 = 2[V], R3 = 6[V], R4 = 6[V]
가 된다.
※ 오옴의 법칙에서 전압은 저항에 비례하여 걸리게 되므로 다음의 수식에 의해서도
계산할 수 있다.
⊙ 저항 I[Ω] = 1 k로 놓으면
1k + 3k + 3k + 2k = 9k =18
k = 2[V]이다.
따라서 R1 = 2 × 2 = 4[V]
R2 = 2 × 1 = 2[V]
R2 = 2 × 3 = 6[V]
R2 = 2 × 3 = 6[V] 이다.
'전기인이 되는 길 > 회로이론' 카테고리의 다른 글
| 전류계, 전압계 접속 (배율기, 분류기) - 회로이론 제5강 (0) | 2021.11.30 |
|---|---|
| 저항의 직·병렬 접속 (직·병렬 연결) - 회로이론 제4강 (1) | 2021.11.28 |
| 저항 (R : Resistance) - 회로이론 제2강 (0) | 2021.11.27 |
| 1. 전류와 전압 : 회로이론 제1강 (0) | 2021.11.27 |
| 전기기초이론 - 전류, 전압, 저항, 비정현파(정의, 전압, 전류, 전력 계산) (0) | 2021.08.25 |
