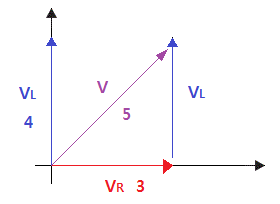
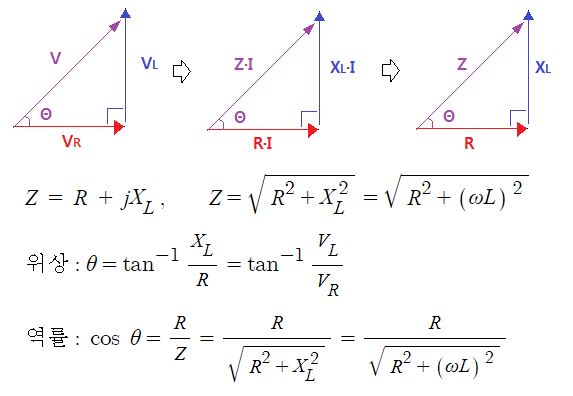
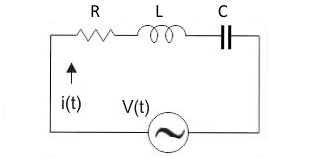
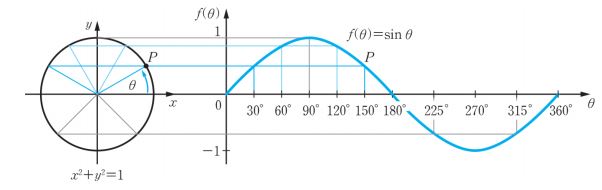
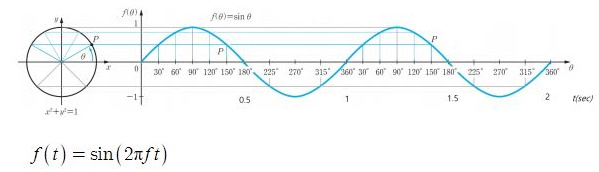
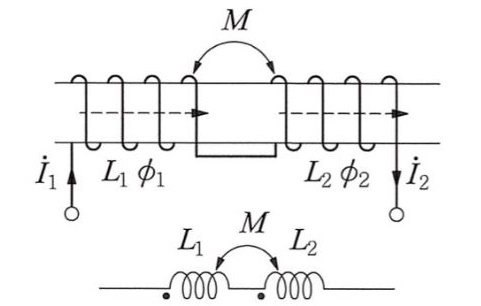
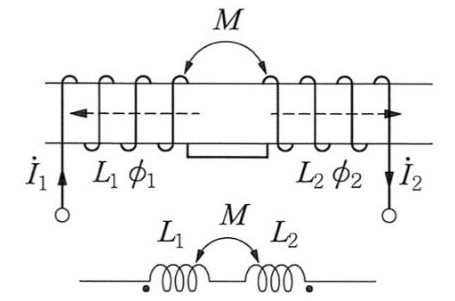
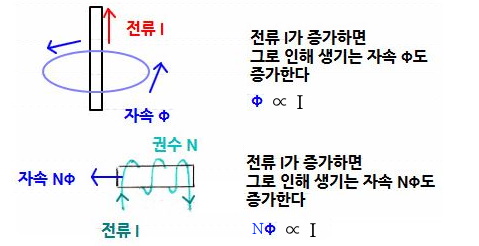
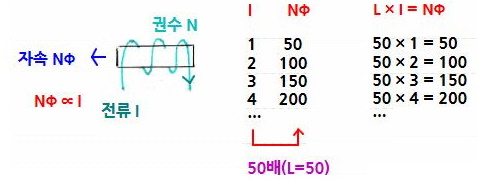
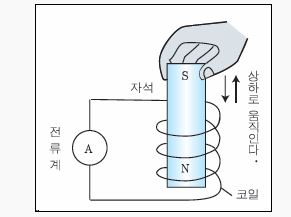
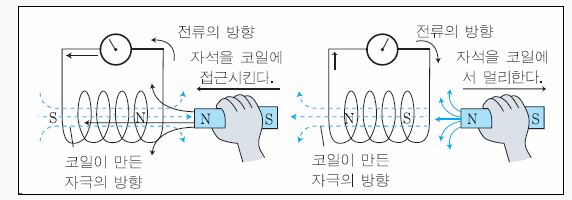
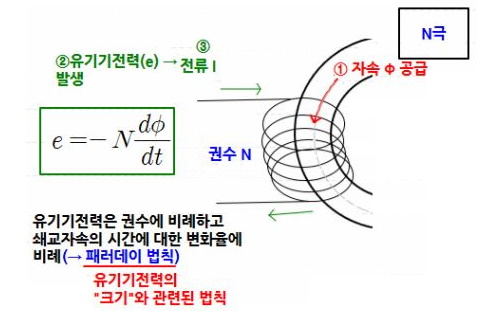
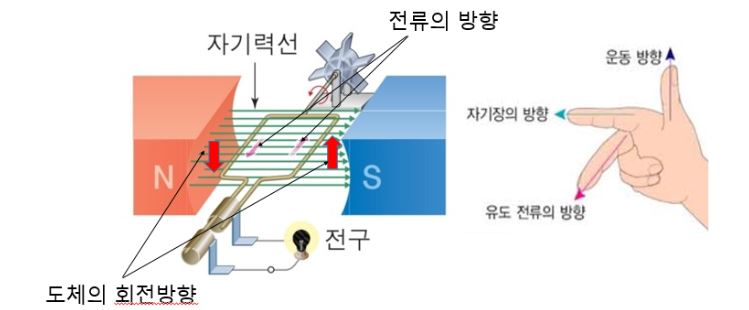
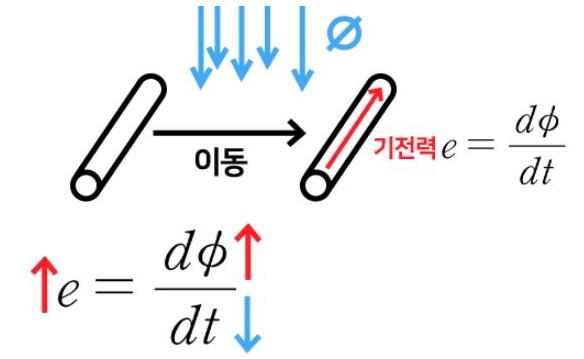
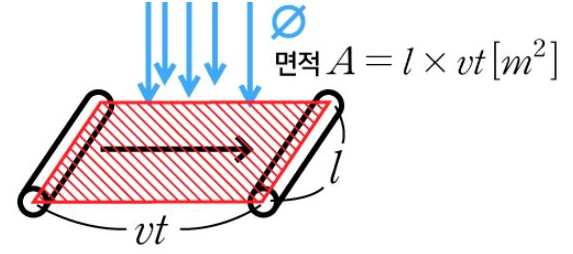
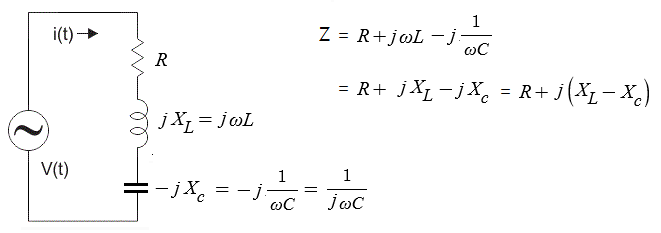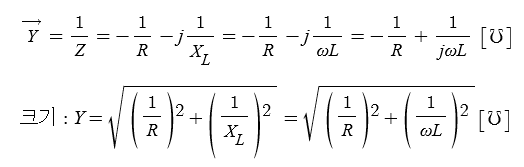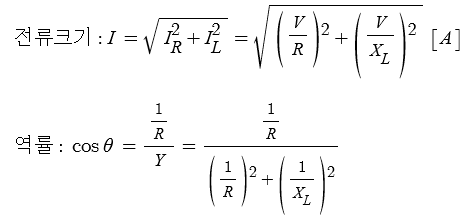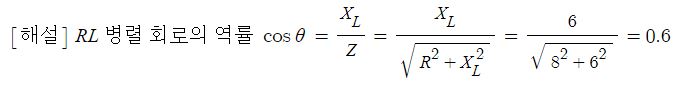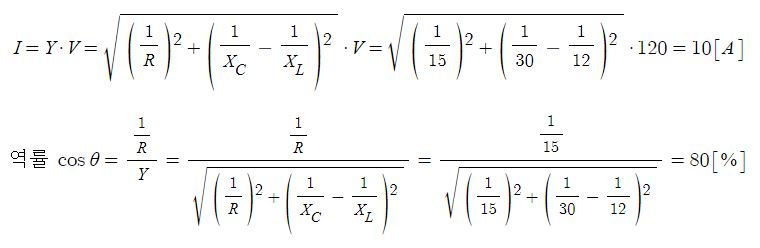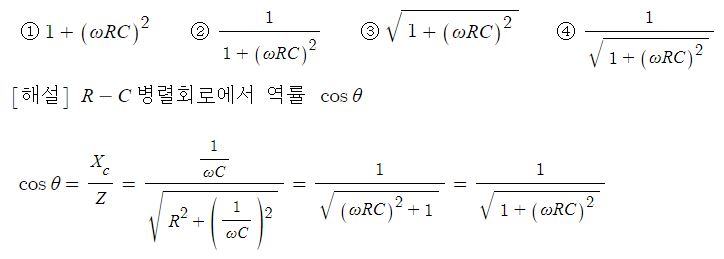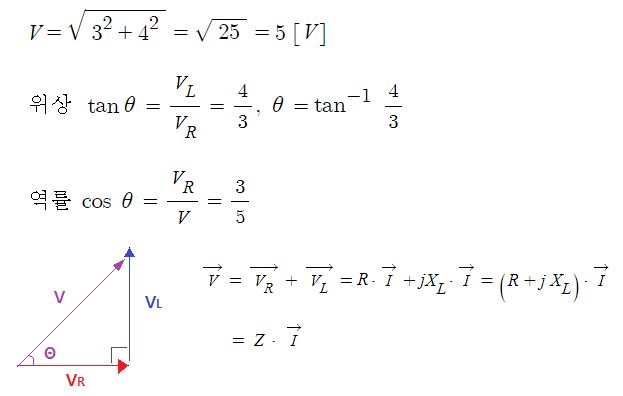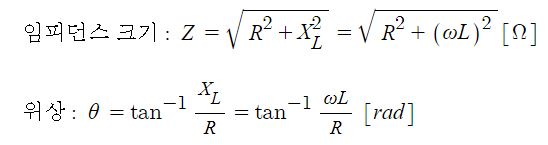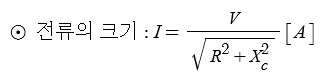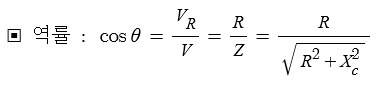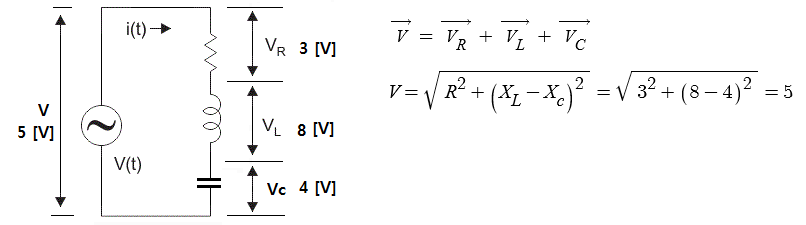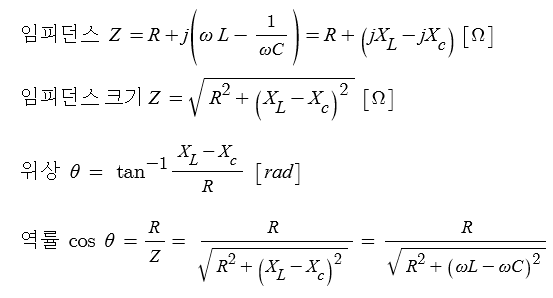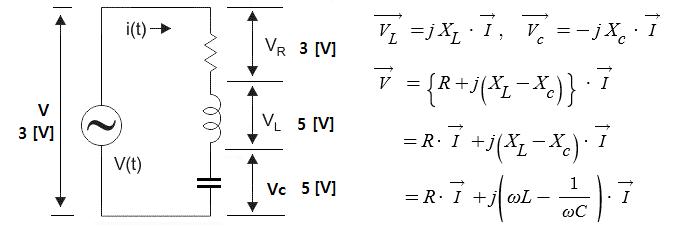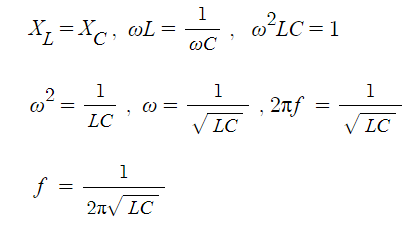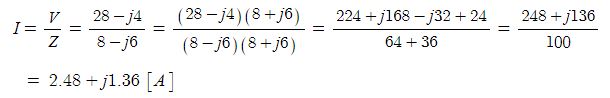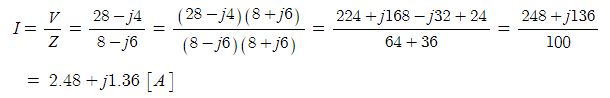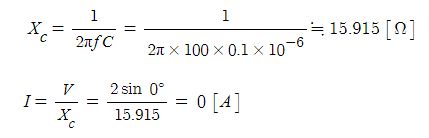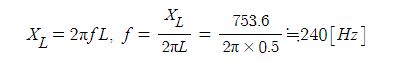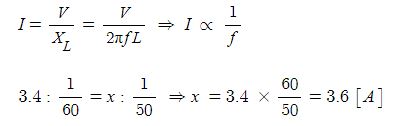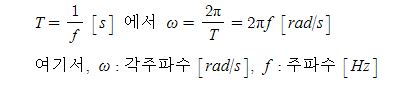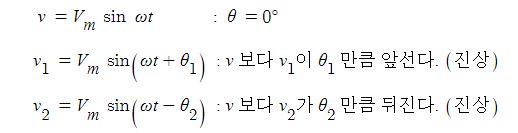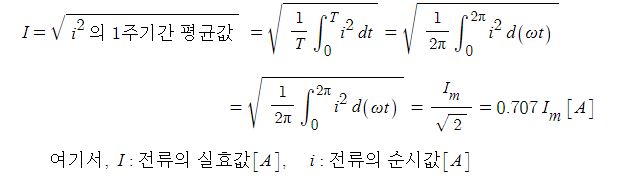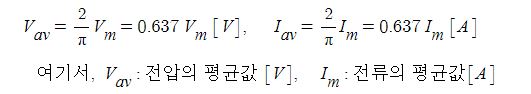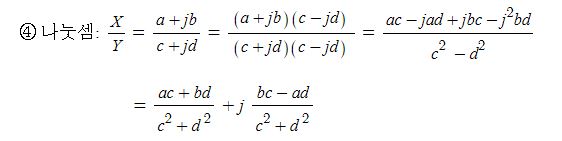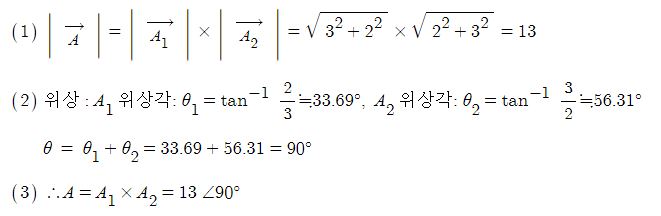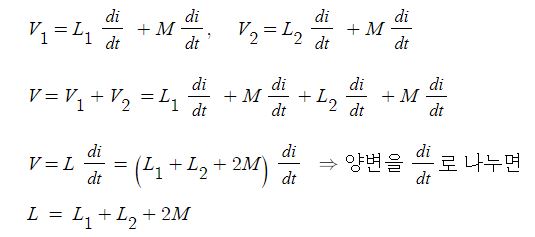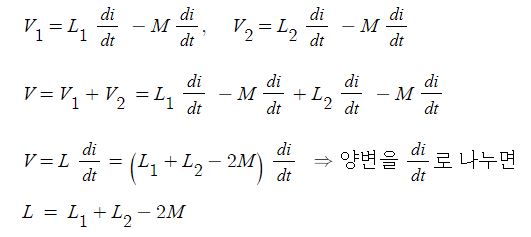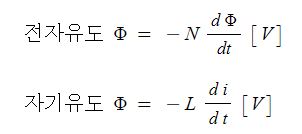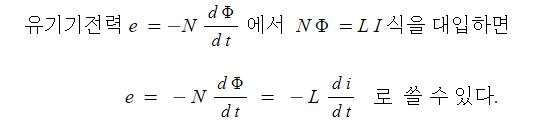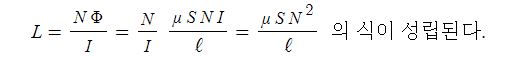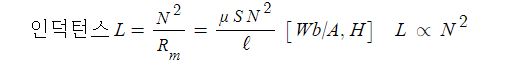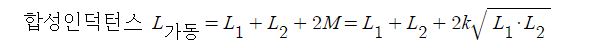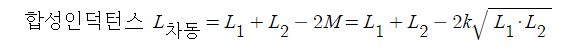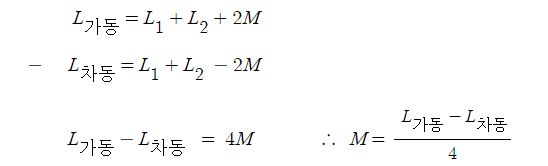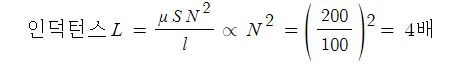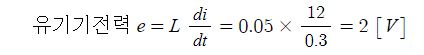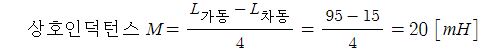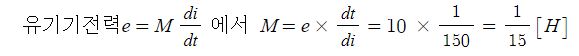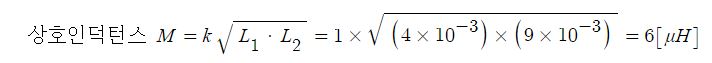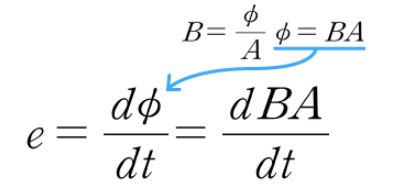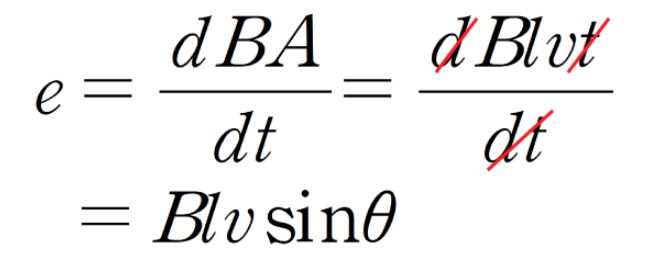▣ 전기에너지와 일률을 혼용하여 사용합니다. 전기는 역학적인 힘을 발생시킨다.
모터가 그런 역할을 한다. 또한 힘이 전기를 발생시키기도 한다. 발전기가 그런 역할을 한다.
이런 이유로 일률 [W]가 전기에너지의 단위도 되고 전기의 일률 단위로도 사용된다.
힘과 에너지, 일률 등에 대하여 먼저 알아 보자.
1. 속도, 가속도, 힘, 일, 일률
가. #속도 (Velocity)
▣ 속도는 얼마시간 동안 얼마만큼 이동했냐를 나타내는 단위다. 즉, 단위시간당 이동한 거리를 나타낸다.
이는 이동한 거리와 소요된 시간과의 비율을 말한다. 속도 v = 거리 s / 시간 t [m/sec] 로 나타냅니다.
나. #가속도 (Acceleration)
▣ 가속도는 얼마의 시간동안 얼마 만큼의 속도가 변했는가를 나타내는 단위다.
즉, 단위 시간당 속도의 변화량을 나타낸다. 예를 들어 어떤 차가 출발하여 5초만에 20 [m/sec]의 속도를 냈다면
이 차의 가속도는 4 [m/sec2]이 된다.
가속도 산정은 ( 20 [m/sec] - 0 [m/sec] ) / 5 [sec] = 4 [m/sec2]
가속도 a = 속도 변화량 v / 시간 t
가속도 1은 1초 동안에 속도 변화가 1[m/sec]이라는 것을 말한다.
다. #힘 (Force)
▣ 힘은 가속도를 발생시키는 원천이다. 정지해 있는 물체를 움직이려면 힘을 가해야 한다.
정지한 물체가 이동하는 순간, 가속도가 발생한다. 뉴턴이 힘을 수식으로 정리했다.
뉴턴의 유명한 수식은 다음과 같다.
F = m · a
힘이란 어떤 질량을 가진 물체의 속도를 변화시키는 양이다. 힘의 단위를 아이작 뉴튼 (Isaac Newton)의 이름을 따서
N (Newton)을 힘의 단위로 사용한다.
1 [N]은 1kg의 물체를 1초 동안에 1[m/sec]으로 가속시키는 힘을 말한다.
1 [N] = 1[kg·m/sec2] 입니다. 힘의 단위는 [kg·m/sec2]를 의미한다.
라. 일 (Work)
▣ 일은 힘을 들여서 물체를 이동시키는 것을 의미합니다. 일은 힘 × 거리로 나타낸다.
W = F · s (일 = 힘 × 거리)
일의 단위로는 J(Joules)을 사용하며 1[J]은 1[N]의 힘으로 물체를 1[m] 옮긴 것을 말한다.
마. #일률 (Power)
▣ 일률은 단위 시간당 일할 수 있는 능력을 말한다. 일할 수 있는 에너지를 의미한다.
단위로는 W[Watt]를 씁니다. 1[W]는 1초 동안에 1[J]의 일을 할 수 있는 능력 (에너지)를 말하고
10[W]는 1초 동안에 10[J]의 일을 할 수 있는 능력, 에너지를 말한다.
일률 P = W[J] / t [sec]
2. 직류전력
▣ 전력은 일률, 에너지를 말한다. 단위는 W를 사용하고 1[W] = 1[J / sec] 입니다. 즉, 1초 동안에 1[J]의 일을 할 수 있는
능력, 에너지를 말한다. 1[J]은 1[N]의 힘으로 1[m]를 이동시키는 일을 의미하고 1[N]은 1초 동안에 1kg의 물체를
1[m/sec2]로 가속시킬 수 있는 힘을 말한다.
▣ 이상은 물리적 측면에서 말한 것이고 전기에서는 전력은 1[V] × 1[A] = 1[W] 이다.
전기에서도 1[W]는 1[J]의 일을 할 수 있는 일률, 능력, 에너지를 말한다. 전압 V는
질량, 전류 I는 가속도 ( I = q/t)에 대응하는 개념으로 보면 된다.

3. 교류전력
▣ 교류에서는 전압과 전류의 값이 순간순간 변화하므로 직류처럼 전력을 P = V × I 로 구할 수 없다.
교류에서는 순시값을 적분하는 방법으로 전력, 일률을 구하게 된다.
변하는 값의 합은 적분을 통해서 구하게 된다.
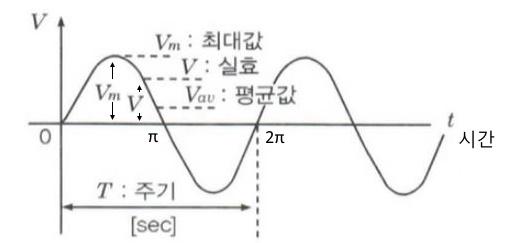
⊙ 교류에서는 전력(일할 능력, 에너지)도 순시값이 변하므로 순시값으로 그 회로를 대표
하는 전력을 나타내는 것은 곤란하므로 평균값으로 그 회로의 전력을 나타내게 된다.

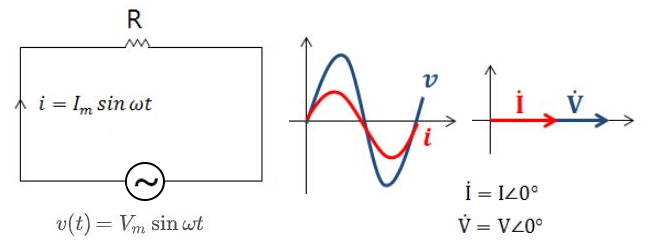
▣ 저항(R)만의 회로에서는 전압 × 전류의 값이 모두 양의 값이 되어 전력( = 전압 × 전류)의 값이 모두 양수가 되고
전력의 주파수는 커지게(증폭) 된다.

▣ 저항(R)만의 회로에서는 전력은 P = V × I 로 구할 수 있다.
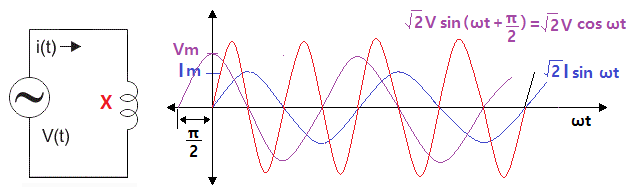
▣ 순시전력을 구해보자. 전력 P = 전압 V × 전류 I 이다.

▣ 평균 #전력 에 대하여 알아 보자.
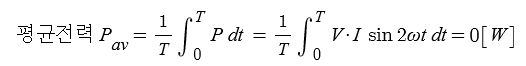
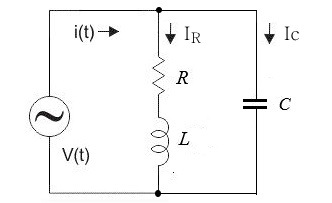
※ L만의 회로에서는 에너지 소모가 없다. 평균전력이 "0"이다.
L만의 회로에서는 충전과 방전을 계속하여 에너지 소모, 전력소모가 없다.
▣ 순시에너지에 대해 알아 보자

다. #콘덴서 C 만의 회로
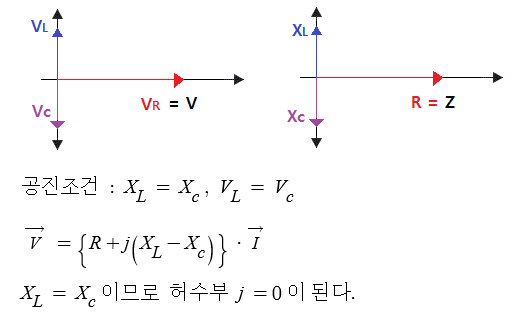
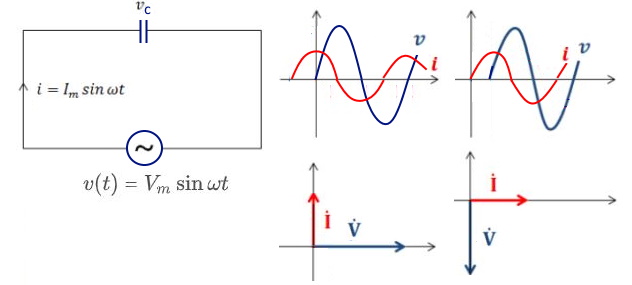
▣ L만의 회로에서는 전류가 전압보다 π/2(90˚)만큼 앞선 진상전류가 흐르게 된다.
⊙ 또한 전류와 전압의 위상차가 있어 극성이 서로 일정하지 않게 된다.
⊙ 전력 P의 파형도 정현파(Sin파)를 이루므로 전체를 단순합산하면 0이 된다.
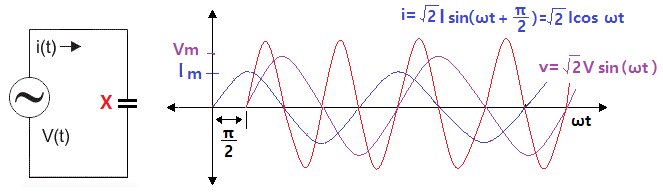
▣ #순시전력 을 알아 보자.
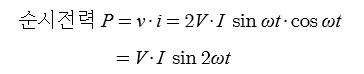
▣ #평균전력 에 대하여 알아 보자.
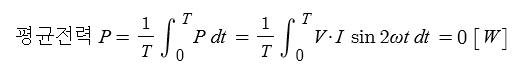
※ C만의 회로에서는 에너지 소모가 없다. 평균전력이 "0"이다.
C만의 회로에서는 충전과 방전을 계속하여 에너지 소모, 전력소모가 없다.
▣ 순시 에너지에 대해 알아 보자.
나. #유효전력 (평균전력, 소비전력) : 실제 일을 하는데 사용되는 전력을 말한다.

다. #무효전력 : 소비되지 않고 충전 되는 전력

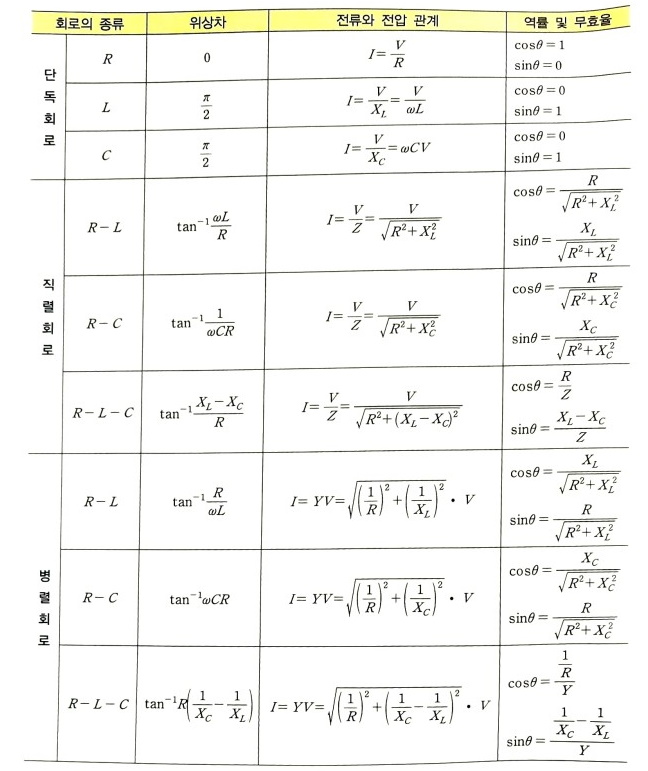
5. 역률과 무효율

6. #복소전력
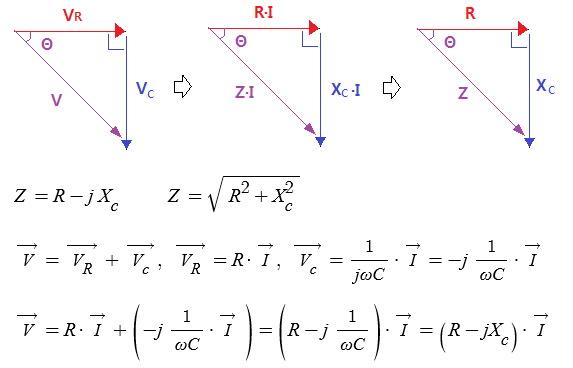
▣ 전력은 #전압 × #전류 이다. 저항에 흐르는 전류와 전압은 위상이 같은데, 리액턴스에 흐르는 전압와 전류는 위상에
차이가 있으므로 벡터적으로 산정해야 한다.
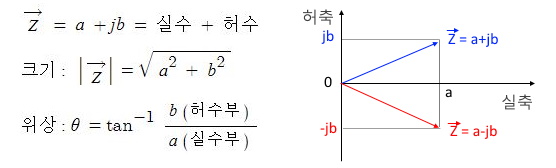
⊙ 다음에 주어진 전압과 전류값으로 #극형식 의 곱으로 전력을 산정해 보자.

▣ 교류전력을 산정하기 위해서는 전압과 전류를 단순하게 #복소수 곱셈으로 계산하면 위상차에 오류가 발생하므로
전압과 전류중 하나의 값을 #컬레 복소수값으로 취해서 전력을 계산한다. 컬레 복소수값을 취하는 것은 위상차를
전압과 전류의 #위상차 로 만들어 주기 위함이다.
|
구 분
|
복소전력
(공액)
|
+j Q
|
- j Q
|
|
전류공액
|
P = V · I
|
유도성
|
용량성
|
|
전압공액
|
P = V · I
|
용량성
|
유도성
|
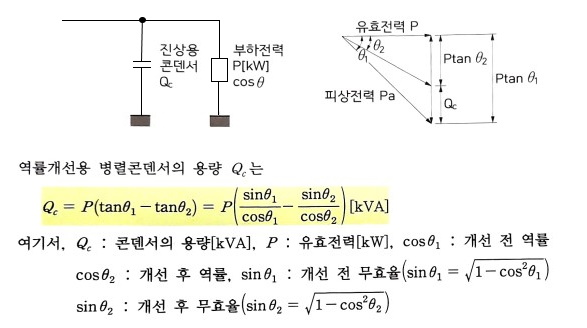
7. #역률 개선을 위한 콘덴서 용량
8. 최대 전력 전송
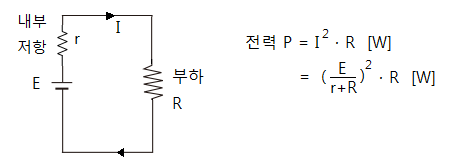
가. 직류에서 최대 전력 #전송
▣ #직류회로 에서는 전압과 전류의 위상차가 없기 때문에 전력 = 전압 × 전류 이며
P = V · I = I^2 · R [W]가 된다.
▣ 이 때 #전원장치 에서 발생한 기전력이 부하에 최대로 전달되는 최대전력 전송조건에 대하여 알아 보자.

▣ 저항과 전력과의 관계를 볼 때, 전력곡선의 접선이 "0"이 즉 미분한 값이 영일 때
전력은 최대가 된다. 이를 통해서 전력의 최대값을 구해 보자.

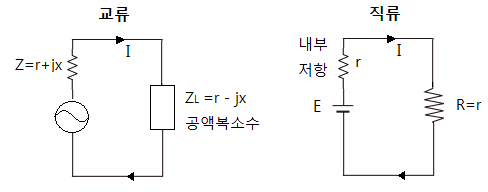
나. 교류 전력
▣ 교류회로에서 내부 #임피던스 와 부하 임피던스에 #리액턴스 성분이 있기 마련이다.
이런 리액턴스 성분 때문에 전압과 전류에 위상차가 발생하게 된다.
▣ 전압과 전류의 위상차 때문에 부하에는 임피던스가 복소수 형태로 발생하는데
직류에서 처럼 전력이 최대가 될려면 내부저항과 부하저항이 같을 때 최대가 된다.
이런 부하전력의 최대조건을 맞추기 위해서는 #부하 임피던스의 허수부가 "0"이 되어야 하고
즉, 임피던스의 #허수부 가 없어질 때 최대전력 전달조건이 된다.
다. 최대전력 전송

【출제 예상 문제】
1. 어떤 회로에 V=100+j20 [V]인 전압을 가했을 때, I=8+j6 [A]인 전류가 흘렀다. 이 회로의 소비전력은 몇 [W]인가 ? ②
① 800 [W] ② 920 [W] ③ 1,200[W] ④ 1,400[W]
[해설] 복소전력 P=VI = (100+j20) (8-j6) = 800-j600+j160+120=920-j440 [VA]
∴ 소비전력은 920 [W]
2. 전압 E=10+j5[V], 전류 I = 5+j2 [A]일 때 소비전력 P와 무효전력 Q는 각각 얼마인가 ? ④
① P=15[W], Q=7[Var] ② P=20[W], Q=50[Var]
③ P=50[W], Q=15[Var] ④ P=60[W], Q=5[Var]
[해설] 복소전력 P=VI = (10+j5) (5-j2)=50-j20+j25+10=60+j5
∴ 소비전력 P=60[W], 무효전력 Pr = 5[Var]
3. 무효전력 Pr = Q일 때 역률이 0.6 이면 피상전력은 ?
① 0.6Q ② 0.8Q ③ 1.25Q ④ 1.67Q
[해설] 피상전력
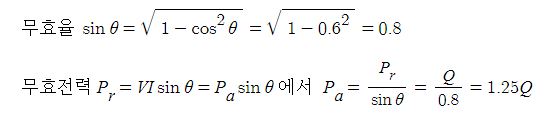
4. 어떤 회로에 v(t)=150sinωt [V]의 전압을 가하니 i(t)= 6 sin(ωt-30°) [A]의 전류가 흘렀다. 이 회로의 소비전력은 ? ②
① 약 390 [W] ② 약 450 [W] ③ 약 780 [W] ④ 약 900 [W]
[해설] 소비전력 P=Pa cos θ = VI cosθ

5. 내부저항 r[Ω]인 전원이 있다. 부하 R에 최대전력을 공급하기 위한 조건은 ? ②
① r = 2R ② R = r ③ R = 2√r ④ R = r2
[해설] 최대전력 전달조건 : 부하저항 = 내부저항, R =r
6. 220[V] 전원에 1.2[kW]의 선풍기를 접속하니 6[A]의 전류가 흘렀다. 이 선풍기의 무효율은 약 몇 [%]인가 ? ②
① 11 ② 42 ③ 55 ④ 85
[해설] 교류전력의 무효율
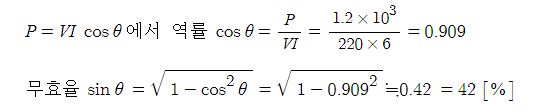
7. 전기회로의 전압 E, 전류 I 일 때 Pa = EI = P+jPr 에서 무효전력 Pr < 0 이다. 이 회로는 어떤 부하인가 ? ①
① 유도성 ② 용량성 ③ 저항성 ④ 공진성
[해설] 복소전력
|
구 분
|
복소전력
(공액)
|
+j Q
|
- j Q
|
|
전류공액
|
P = V · I
|
유도성
|
용량성
|
|
전압공액
|
P = V · I
|
용량성
|
유도성
|
8. 역률 90[%] 450[kW]의 유도전동기를 95[%]의 역률로 개선하기 위하여 필요한 콘덴서의 용량 [kVA]은 ? ③
① 약 25 ② 약 48 ③ 약 70 ④ 약 95
[해설] 역률 개선을 위한 콘덴서 용량
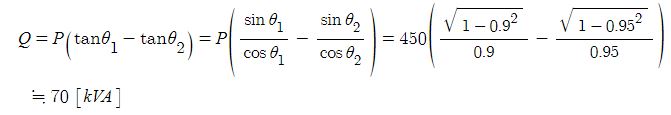
9. 그림과 같은 회로에서 부하 RL에서 소비되는 최대전력은 몇 [W]인가 ? (단, Rs는 전원의 내부저항이다)

① 12 [W] ② 36 [W] ③ 72 [W] ④ 144 [W]
[해설] 최대 전력 공급 조건

'소방설비기사 (전기) > 소방전기일반' 카테고리의 다른 글
| 교류 전력 측정, 계측기 오차 보정 (2) | 2023.02.16 |
|---|---|
| 3상, n상 교류 전력, Y-△ 결선 임피던스 변환 (0) | 2023.02.14 |
| 교류 R-L-C 병렬 회로, R-L-C 병렬 공진 (0) | 2023.02.13 |
| 교류 R-L-C 직렬 회로, R-L-C 직렬 공진 (0) | 2023.02.12 |
| 교류회로의 기본 소자 : 수동 소자 (0) | 2023.02.11 |
비버리님의
글이 좋았다면 응원을 보내주세요!