아낌없이 주는 나무

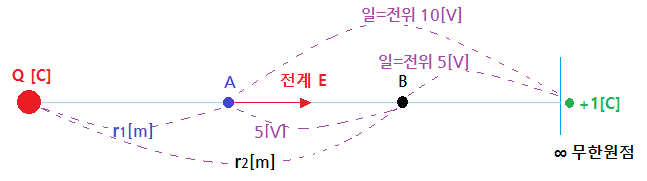
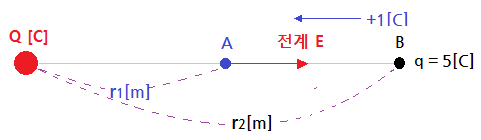
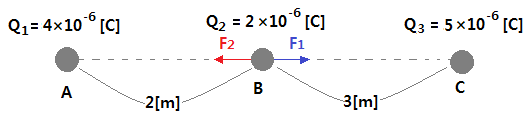
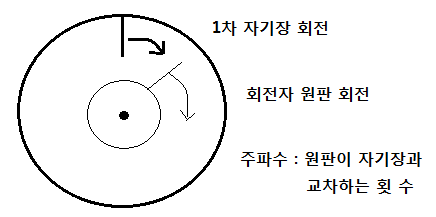
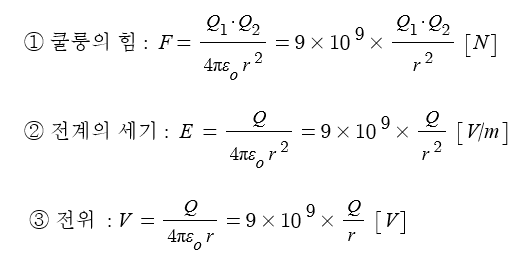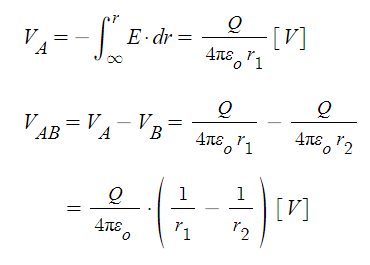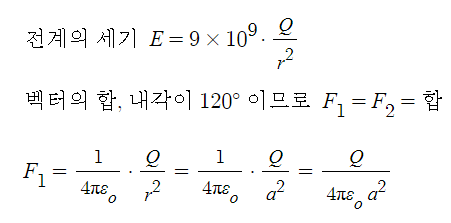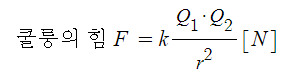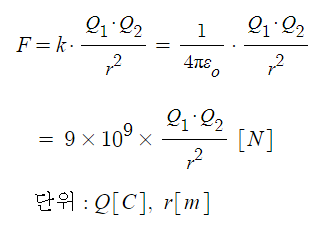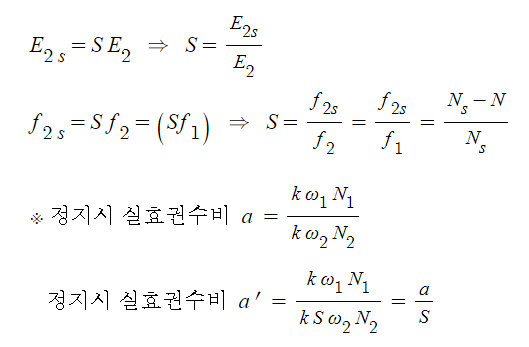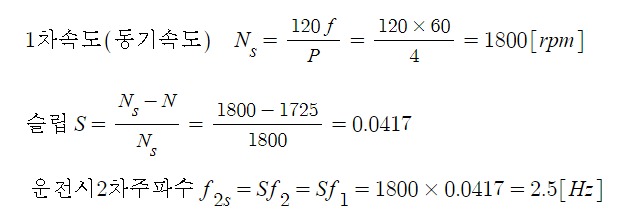▣ 동기발전기 전기자 반작용

​

⊙ 아래 발전기의 등가회로를 보면서 전기자 반작용에 대해 알아보자.

⊙ 위의 발전기의 등가회로를 보면 계자에서 자속을 공급하면 전기자 권선이 기계적

    회전 운동으로 계자의 자속을 끊게 되고 전선이 주위의 자속을 변화가 생기면

    페러데이의 전자유도 법칙에 의해 전기자 권선에 유기기전력(E)이 발생하게 된다.

​

유기기전력(E)은 권선에 전류를 흐르게 하고 이 전기자 전류(Ia)를 흐르게 하고

이 전기자 전류(Ia)는 다시 권선 주위에 회전자계를 발생시키는데 이 회전자계는

계자 자속에 영향을 주게 되는데 이러한 작용을 전기자 반작용이라 한다.

​

한편 부하의 종류에 따라 전기자 전류 (Ia = I)의 위상을 변화시키는데 저항부하 R은

유기기전력과 동상이고, L 부하는 지상, C부하는 진상 전류를 흐르게 한다.

이에 따라 부하에 발전기의 전력에도 영향을 주게 된다.

​

R 부하 : P = V · IR = V I cos Θ [VA]

L 부하 : Pr = V · IL = V I sin Θ [VA]

​

전기자 반작용은 전기자 권선에 흐르는 전류(Ia)에 의해 발생하고, 이 전기자 전류(Ia)는

부하전류와 같은 전선을 흐르므로 정격전류와 같다. 그런데 무부하 상태에서는 전류가

흐르지 않으므로 전기자 반작용도 발생하지 않는다.

따라서 전기자 반작용은 부하가 있을 때 즉, 전류가 흐를 때만 발생한다.

​

한편 전기자 반작용은 부하의 성질에 따라 반작용의 영향이 달라 진다.

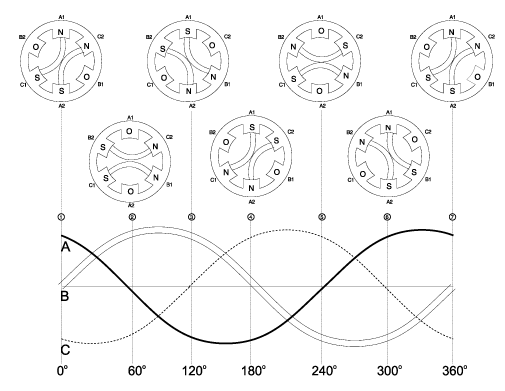
아래 그림을 보면서 R. L, C 부하에 따라 전기자 반작용이 어떻게 변화하는지 알아보자

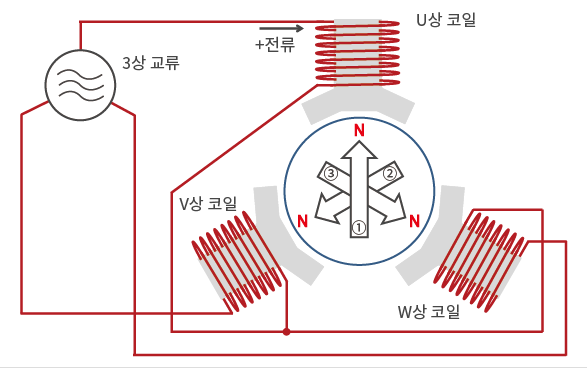
위 그림에서 전기자 전류가 최대일 때의 전기자 반작용에 대하여 알아 보자

계자에서 자속이 공급되면 자속은 N극에서 S극으로 흐르게 되고

기계적 회전운동으로 전기자 권선이 자속을 끊게 되어 전기자 권선에는 Ia의 전류가

흐르게 되고 이 전기자 전류는 다시 주자속에 영향을 주는 자속을 발생시키게 된다.

전기자 권선에서 발생하는 자속은 전기자 권선이 계자극에서 가까울 때 최대가 되고

멀어질 때 자속발생은 작아진다. 따라서 전기자 권선이 0˚와 180˚일 때 자속, 전류가

0이 되고 90˚, 270˚일 때 자속, 전류는 최대가 된다.

전기자 권선이 90˚ 회전할 때에 전류의 방향을 보면 전기자 전류는 들어가는 방향이

된다. 즉 전류가(+)일 때는 들어가는 방향이고 전류가 (-)일 때는 나오는 방향이 된다.

​

이제 부하의 종류에 따른 전기자반작용을 알아 보자.

위 그림에서 먼저 R부하에 대하여 알아 보자

저항부하일 때는 유기기전력과 전류는 동상이고 유기기전력이 최대일 때, 전기자전류도

최대가 된다. 전기자 권선에서 발생하는 회전자계는 N극 주변에서는 들어가는 방향,

S극 주변에서는 나오는 방향이 되어 합성 회전자속은 계자에서 발생하는 주자속과

직각방향 즉, 횡축으로 작용하게 된다. 주자속과 전기자 반작용 자속이 서로 교차하게 되어

교차자화작용이라고 부르며 계자의 N극과 S극 주변에서는 한쪽은 약간 증자,

한쪽은 약간의 감자현상이 발생하여 중심축이 약간의 편차현상이 발생하게 되고

전체적으로 계자의 주자속이 감소하하는 감자현상이 발생하게 된다.

​

L부하 일 때를 알아 보자.

발전기의 유기기전력에 의해 흐르게 되는 전기자 전류(Ia)가 L부하를 만나면 유기기전력

보다 90˚ 위상이 늦은 지상전류가 되고 유기기전력보다 위상이 90˚ 늦어 최대 전류가

흐르게 된다. L부하 일 때 전기자가 만드는 회전자계의 합성 자속은 계자가 만드는 주자속

과 반대 방향으로 발생하게 되고 이로 인해 주자속을 감소시키게 된다.

회전자계가 만드는 합성자속은 주자속 축과 평행하다 하여 직축반작용이라 부른다.

​

C부하 일 때에 대하여 알아 보자

발전기의 유기기전력에 의해 흐르게 되는 전기자 전류(Ia)가 C부하를 만나면 유기기전력

보다 90˚ 위상이 앞선 진상전류가 되고 유기기전력보다 위상이 90˚ 앞서 최대 전류가

흐르게 된다. C부하 일 때 전기자가 만드는 회전자계의 합성 자속은 계자가 만드는 주자속

과 같은 방향으로 발생하게 되고 이로 인해 주자속을 증가시키게 된다.

회전자계가 만드는 합성자속은 주자속 축과 평행하다 하여 직축반작용이라 부른다.

​

R 부하 ⇒ I cos Θ - 횡축반작용

- 교차자화작용, 약간의 감자작용

​

L 부하 : 뒤진전류, 감자작용 (φ 감소 ↓) ⇒ 유기기전력 감소 (E ↓) ⇒ 부하전압 감소 (V ↓)

+ I sin Θ

​

C 부하 : 앞선전류, 증자작용 (φ 증가 ↑) ⇒ 유기기전력 증가 (E ↑) ⇒ 부하전압 증가 (V ↑)

- I sin Θ

【 전위 [V] 】

1. 전위 : "일" = 힘 × 이동한 거리 = F · r [V]

​

▣ 전위는 일의 다른 표현이다. 일은 특정 힘으로 대상물을 옮긴 거리로 볼 수 있다.

    즉, 일은 힘 × 이동한 거리로 표현할 수 있다.

▣ 전위를 설명하기 전에 우선 "일"에 대하여 알아 보자

가. 전위의 정의

  ▣ 전위 : 전계의 세기가 E인 평등전계내에서 P점의 전위란 ?

   ⊙ 무한 원점으로 부터 단위 점전하(+1[C])를 전계에 대항하여 P점까지 이동시키는데

       소요되는 일 (힘 × 이동거리)

▣ 전위란 위 그림과 같이 무한원점에 있는 +1[C] 전하를 P점으로 옮기는데 소요되는 일이

    다. 전위를 구하기 위하여 힘과 거리로 나누어 일량을 구해 보자.

【 기본 적분식 】

 ▣ 전자기학 공부에 필요한 기본적분식에 대하여 알아보자.

▣ Q[C] 전하로 부터 r[m] 떨어진 지점의 전위는 ?

【 정리 】

​

​【 전위 경도 】

1. 전위차

가. Q[C]의 전하에서 r1[m] 떨어진 A와 r2[m] 떨어진 B 간의 전위차

   ▣ 전위차 : +1 [C]의 단위전하를 B점에서 A점으로 이동하는데 소요되는 일

▣ 위 그림에서 전위차는 VA와 VB의 전위의 차이를 말하는 것으로 +1[C]의 단위전하를

    B점에서 A점으로 옮기는데 소요되는 에너지(일)를 말한다.

  ⊙ 전위차 VAB = VA - VB

나. A,B점 사이에 q[C]을 이동시킬 때 소요되는 일

▣ B점에서 A점으로 +1[C]의 단위 전하를 이동하는데 소요되는 일이 전위이므로

    B점에서 A점으로 q[C]을 옮기는데 소요되는 일은 전위차 × q[C]이 된다.

다. 전위의 기준

① 전위의 기준은 "무한원점"을 기준으로 한다.

② 무한원점의 전위는 "0" 전위이다.

    ※ 일 = 힘 × 이동한 거리 = +1[C] × "0" = "0"

​

라. 전계의 보존성

  ▣ Q[C]의 전하에 의하여 만들어진 전계내에서 단위 정전하를 폐회로에 따라 일주

      시킬 때 "전계 E가 하는 일"은 "영(0)"이다.

※ 정전하가 이동하여 제자리로 돌아 오면 이동하면서 소비된 에너지 만큼 제자리로

    돌아 오기 위해서는 전위를 외부에서 공급받아야 하므로 결국 소요된 전위(에너지)는

    없게 된다.

​

2. 전위 경도 ※ 경도 : 기울기

​가. 전위의 경도 (전위의 기울기)

    ※ 기울기를 구하라는 말은 미분하라는 말과 같다.

나. 임의의 거리를 진행할 때 (임의의 두 점 사이의) 전위의 높이 변화

    ⇒ 단위 길이당 전위의 변화

다. 전위

【 종합정리】

 전계 E = - grad V (전위의 기울기) - 는 방향이 반대라는 의미이다.

   ※ 전위의 경도는 전계의 세기와 크기는 같고 방향이 반대라는 의미이다.

​

​

1. 전계

전계 : 어느 공간에 대전체가 존재하여 공간상에 전기적 힘이 작용하고 있는 공간을 전계라고 한다.

정전계 : 전계 중에서 전계 에너지가 최소로 되는 전하 분포의 상태의 전계를 정전계라고 한다.

​

2. 전계의 세기 (E)

▣ 정의 : Q[C]으로 부터 거리가 r[m] 떨어진 거리에 단위 정전하(+1[C])를 놓았을 때

            이 단위 정전하에 작용하는 쿨룽의 힘을 그 점의 전계의 세기로 표현한다.

 ※ 이 때 전계의 세기에 영향을 미치는 것은 Q [C]의 전하 즉 전하량(대전체, 대전된 정도)과

    Q [C]의 전하로 부터 떨어진 거리에 영향을 받게 된다.

가. 전계의 세기 (힘의 크기)

▣ 전계의 세기 : 전계내에서 단위 정전하(+1[C])가 받는 쿨룽의 힘

   ⊙ 전계의 세기는 단위 정전하(+1[C])가 받는 힘이므로 전계의 세기는 오로지 전계내에 작용하는 힘에

       크기에 의하여 좌우되며 단위 정전하는 영향을 받는 역할만 하게 된다.

  ※ 쿨룽의 힘은 공간상에 존재하는 전하들간에 서로 작용하는 힘이므로 전계의 세기를 계산할 때

      쿨룽의 힘의 법칙에 의하여 단위 정전하 (+1[C])가 미치는 힘의 크기는 +1 이므로 단위정전하에

      의한 힘의 영향은 제외하고 오로지 공간상에 작용하는 힘의 세기를 나타내게 된다.

      쿨룽의 힘에 의하여 전계의 세기를 계산하므로 쿨룽의 힘은 거리의 제곱에 반비례하고 각각의

      전하의 전하량에 의해 영향을 받게 되고 전하가 놓여 있는 매질에 의해 영향을 받게 된다.

      따라서 전계의 세기는 쿨룽의 힘을 Q[C]으로 나누어 준 것과 같게 된다.

나. 전계의 세기 (힘의 방향)

▣ 전하들간에 서로 작용하는 힘은 대전체의 극성에 따르게 되는데 전하들간에

    다르면 극성이면 끌어당기는 흡인력이 작용하고 극성이 서로 같으면 밀어내는 힘

    즉, 반발력이 작용하게 된다.

▣ 단위 정전하가 양전하이므로 Q전하가 양(+)전하이면 반발력이 발생하고

    Q전하가 음(-) 전하이면 흡인력이 발생한다.

​

3. Q[C]전하로 부터 r[m] 떨어진 곳, P점에 q [C]의 전하를 놓았을 때 작용하는 힘

가. P점에 +1[C](단위 정전하)을 놓았을 때 작용하는 힘

  ▣ Q[C]으로 부터 r[m] 떨어진 곳에 단위 정전하 (+1[C])를 놓았을 작용하는 힘은 Q[C]의 전하와

      단위 정전하간에 작용하는 쿨룽의 힘을 계산하면 된다. 쿨룽의 힘은 거리의 제곱에 반비례하고

      공간의 매질에 영향을 받는다.

 ▣ 다만, P 점에 단위 정전하 (+1[C])을 놓았을 작용하는 힘은 오로지 해당 공간상에 작용하는 힘을

      말하며 단위 정전하에 의해 발생하는 힘은 제외된다. 단위 정전하가 작용하는 힘은 "1"이므로

      단위 정전하에 의한 힘은 제외된다.

나. P점에 q[C]의 전하를 놓았을 때 작용하는 힘

    ⇒ 작용하는 힘이 q배로 증가한다.​

​ ▣ P 점에 q[C])을 놓았을 작용하는 힘은 공간상에서 발생하는 쿨룽의 힘을 말하며

     Q[C], q[C]이 상호작용하는 힘을 말한다.

【전계의 세기 예제 문제 풀이】

ex1 : 공기중에 2×10-7[C]의 점전하를 놓았을 때 이로 부터 50[cm] 거리에 있는

       점 P에서의 전계의 세기 [V/m]는 ?

 ※ Q[C]으로 부터 50[cm] 떨어진 곳에 단위 정전하를 놓았을 때 작용하는 전계의 세기는

    쿨룽의 힘 산정식으로 계산할 수 있다. 이때 단위 정전하가 작용하는 힘은 "1"이므로

    Q[C]이 작용하는 힘만 계산하게 된다.

ex2. 전계의 세기가 500[V/m]인 전계내에 5[μC]의 전하를 놓았을 때 이 전하에 작용

      하는 힘은 ?

 ※ 전계의 세기는 전계내에 단위 정전하 (+1[C])을 놓았을 때 이 단위 정전하가 받을 힘을 말하므로

    단위 정전하 대신에 5[μC]을 놓았을 때 작용하는 힘을 계산하면 전계의 세기에 전계내에 놓은

    전하량을 곱하여 산정하게 된다.

ex3. 한변의 길이가 A[m]인 정삼각형의 두 정점에 Q[C]과 -Q[C]의 점전하를 놓았을 때

      나머지 정점의 전계의 세기 [V/m]는 ?

※ 전계의 세기는 +1[C]의 전하를 놓았을 때 작용하는 쿨룽의 힘이므로

   정삼각형의 정점에 +1[C]이 받는 힘을 구하면 된다.

 ① 위 그림에서 +1[C]의 전하를 놓으면 +Q과는 반발력이 작용하고

     -Q[C]은 흡인력이 발생하므로 힘의 벡터 표시는 위 그림과 같으며

     이들의 합은 벡터합인데 크기가 같고 내각이 120˚인 경우 내적을 구하면

     각각의 벡터와 같게 된다.

 ② 위의 내용을 이용하여 전계의 세기를 구해보자.​

​

1. 대전, 대전체, 전하량

※ 중성물체가 전기를 띠게 되는 현상을 대전이라 부른다.

   중성물체는 양전하와 음전하가 같은 수가 있어서 전기를 띠지 않으나

   음전하 중에 자유전자가 이동을 하여 양전하의 수와 음전하의 수가 달라졌을 때

   전기를 띠게 되는데 이를 대전되었다고 한다.

​

▣ 대 전 : 중성물체가 전자의 이동으로 전기를 띠게 되는 현상

▣ 대전체 : 전기를 띠는 물체

​

① A 물체의 전기량 : + 1.602 × 10-19 × 3개 + Q [C]

① B 물체의 전기량 : - 1.602 × 10-19 × 3개 - Q [C]

   ※ 전기량을 전하량이라 부른다.

​   ※ 양전하, 음전하의 수의 차이가 전기량이므로 전기를 띠게 되는 그 전하량의 차이,

      전기를 띠게 하는 전하의 량을 전기량이라고 한다.

2. 정전유도 현상

▣ 중성물체 A에 대전체 B를 가까이 대면 성질이 다른 전하는 서로 흡인력이 발생하여

    서로 당기게 되고 성질이 같은 전하는 서로 밀어내는 반발력이 작용하게 된다.

▣ 이러한 전하의 성질에 따라 A에 B와 가까운 쪽은 반대극성을 띠는 전하가

    먼쪽은 같은 극성의 전하가 나타나게 된다.

​

3. 쿨룽의 법칙

  ▣ 정지된 두 전하사이에 작용하는 힘에 관한 법칙

 ⊙ 힘은 벡터량으로 크기와 방향을 가진다.

  ※ 같은 극성의 전하간에는 밀어내는 힘(반발력)으로 작용하고

      다른 극성의 전하간에는 끌어 당기는 힘(흡인력)으로 작용한다.

【쿨룽의 법칙】

 ① 힘은 두 전하의 크기에 비례

 ② 힘은 두 전하사이의 거리의 제곱에 반비례

③ 쿨룽상수 : k

  ▣ 두 전하 Q1, Q2 가 놓여 있는 매질(공기, 기름...)에 의해 결정되는 계수

④ 유전율 : ε

  ▣ ε : 유전율 [F/m] : 전하를 유도하는 능력(성질)

  ▣ εo : 진공 또는 공기중의 유전율

   ⊙ εo : =8.855 × 10-12 [F/m]

   ⊙ εs : 비유전율 (비교 유전율)

    ※ 공기의 유전율을 기준으로 하여 다른 물질의 유전율을 비교한 값

※ 공기의 비유전율

【힘의 크기】​

【종합정리】

  ▣ 힘 = 크기 + 방향

  ▣ 방향

   ⊙ 같은 극성의 전하

⊙ 다른 극성의 전하

결과 : 두 전하 사이에 작용하는 힘인 쿨룽의 힘은 두 전하를 연결하는

        직선과 일치한다.

​

【쿨룽의 법칙, 예제 문제 풀이】

ex 1. 진공중에 두 전하가 일직선상에 놓여 있을 때 B전하에 작용하는 힘[N]은 ?

【문제풀이】

  ▣ A, B, C 전하는 모두 양전하이므로 서로간에 반발력이 작용한다.

  ▣ B전하에는 A전하의 반발력 F1, C전하의 반발력 F2가 동시에 작용한다.

  ▣ F1과 F2는 작용하는 힘의 방향이 반대이므로 양 힘의 합은 두 힘간의 차이다.

   ① 먼저 A전하에 의한 힘의 F1을 구해 보자.

② C전하에 의한 작용하는 힘 F2를 구해 보자.

③ B구에 작용하는 힘은 F1 - F2이다.

ex2 : 한변의 길이가 2[m]가 되는 정삼각형의 세정점 A, B, C에 10-4[C]의 전하가 있다.

이 때, 점 B에 작용하는 힘[N]은 ?

【문제풀이】

  ▣ 정삼각형의 각 정점에 크기가 같고 거리가 같은 전하가 놓여 있으므로 작용하는 힘은

     같으나 방향이 다르므로 작용하는 힘의 합은 벡터합으로 구해야 한다.

① A에 의해 작용하는 힘 F1 과 B에 의해 작용하는 힘 F2를 구해 보자.

  ※ 두 전하간에 작용하는 힘은 쿨룽의 법칙에 의하여 계산할 수 있다.

     여기서 9 × 10^9의 공기중의 유전율로 나눈 값이다.

▣ 두 힘의 합은 벡터 합으로 구한다.

  ※ 벡터의 합은 코사인 법칙에 의하여 계산할 수도 있고 삼각함수와 평행사변형에

     의한 방법 등을 이용하여 계산할 수 있다.

1. 동기기의 무부하, 단락시험

​

동기기의 기계적 파라미터값을 측정하기 위해 특성시험을 한다.

동기기의 특성 시험에는 무부하 전압시험과 단락전류 시험이 있다.

만약 동기기의 동기 임피던스를 구한다고 한다면 어떻게 할까?

임피던스는 저항과 리엑턴스로 구성되어 있으므로 저항과 리엑턴스를 측정해야 한다.

동기기를 실제 저항과 리액턴스를 실측하여 이를 합하여 동기임피던스를 구할 수도 있지만

실무적으로 쉽지 않은 일이다.

​

따라서 동기임피던스를 실측에 의해 측정하는 방법의 대안으로 특성시험을 통해

동기임피던스를 구하는 방법으로 특성시험을 하게 된다.

​

특성시험을 통하여 구한 동기임피던스는 전압변동률을 구하는데 중요한

요소가 된다.

​

동기기의 전압변동율을 측정해야 한다면,

직접 무부하 전압과 전부하 전압을 측정하여 전압변동율을 구할 수 있겠지만

동기임피던스의 값을 알게 되면 운전조건을 참조하여 전압변동율을 구할 수 있다.

이러한 동기임피던스값을 구하기 위해 개방회로시험과 단락회로 시험을 하게 된다.

개방회로 시험과 단락회로 시험을 통해 동기임피던스의 값을 구할 때는 실제

임피던스의 크기를 구하는 것보다 %임피던스(%Z)

즉, 정격전압 분의 임피던스 전압강하의 비율을 통해서 임피던스를 구하게 된다.

​

(1) 개방회로 시험

​

개방회로 시험은 부하측 회로를 개방한 상태에서 진행하는 시험이다.

시험조건은 회전자를 동기속도로 운전하는 상황에서 시험하게 된다.

부하단자회로를 개방한 상태에서 회전자의 회전속도를 동기속도까지 올리게 되면

전압은 무부하 포화곡선을 이루게 되고 결국 이 시험은 개방회로 즉 무부하 상태에서

계자전류와 전압간의 관계, 무부하 포화곡선을 얻는 것이 된다.

​

전기자권선의 출력단자는 개방되어 있으므로 출력단자에는 전류가 흐르지 않습니다.

따라서 출력단자 전압은 온전히 계자전류에만 영향을 받게 되고 동기기의 출력전압이

출력단자 전압이 되며 이 출력단자전압을 전압계를 이용하여 측정하게 됩니다.

​

무부하 상태에서 출력이 정격전압이 되는 계자전류의 값은 %임피던스 구하는 식에서

정격전압과 같은 기준이 된다. 무부하 상태에서는

출력전압이 오로지 계자전류에만 영향을 받으므로

정격전압값을 정격전압을 만드는 계자전류의 값으로 대체하는 것이다.

Vn ∝ If 이므로 무리가 없다.

​

동기기는 Y결선을 하므로 출력단자에 1/√3을 곱하면 동기기의 상전압이 된다.

​

(2) 단락회로 시험

​

단락회로 시험은 출력단자를 단락한 상태에서 진행하는 시험이다.

이 시험역시 출력단자를 단락한 상태에서 회전자의 회전속도를 동기속도까지 올리게 되고

이 때 계자전류를 서서히 올리면 출력단자에 전류가 높아지게 되며 출력단자의 전류는

오로지 동기임피던스에만 영향을 받게 됩니다. 출력단자에 정격전류가 흐르게 하는

계자전류값을 측정하게 됩니다. 이 시험으로 계자전류에 대한

단락회로전류의 관계를 알 수 있으며 정격전류를 흐르게 하는 계자전류의 값은

%임피던스 구하는 식에서 %임피던스 전압강하값에 해당합니다.

따라서 %임피던스는 다음과 같이 구할 수 있습니다.

이러한 관계는 발전기의 유기기전력과 단자전압과의 관계를 생각하면 이해가 쉽다.

발전기에서 단자전압 V = E - Ia ·ra 이다. 단자전압 V ∝ E ∝ If 이다.

위식에서 단자전압 "V = 유기기전력 - 전기자반작용 전압강하 " 이므로

단자전압을 발생하는데 소요되는 계자전류와 전기자반작용 전압강하 (동기임피던스

전압강하)가 생기게 하는데 소요되는 계자전류의 비율이 %퍼센트 임피던스와

같은 값이 된다. 발전기 등가회로에서 단자전압은 유기기전력에서 전기자 반작용

전압강하(=동기임피던스전압강하)를 뺀 값으로 정격전압을 만드는데 소요되는

계자전류이고 단락시 정격전류를 만드는데 필요한 계자전류는 다른 말로 동기임피던스

전압강하를 만드는데 소요되는 계자전류라는 말이 되므로 %Z를 구하는 식에 그대로

반영해도 된다.

​

이 관계는 단락비를 구하는데도 그대로 적용할 수 있다.

단락비 Ks = 1 / %Z 이므로 %Z의 관계를 역수로 취하면 된다.

이러한 관계를 나타낸 곡선을 통해 단락회로 특성을 알 수 있습니다

​

아래 그림은 개방 및 단락 회로 시험의 결선도와 측정시험 결과를 나타낸 것입니다.

계자를 동기속도로 운전하여 개방시험을 하여 계자전류에 해당하는 전류와 전압을 측정하였다.

계자전류를 일정하게 하고 동기속도로 운전하였으므로

동일한 계자전류에 대하여 동일한 유기전압이 발생한다고 가정할 수 있습니다

외부의 전원 소스가 없는 상태에서 유기전압만이 유일하 전원이면 이 때 측정된 단자전압과

전기자 전류의 비가 바로 동기임피던스의 값이 됩니다.

​

단자전압의 포화특성으로 시험에서 포화가 된 후에 측정한 동기임피던스의 값은 일정하지 않습니다.

이러한 경우 정격의 전기자 전류가 얻어지는 계자전류에 대하여 동기임피던스를 산정하여 사용하게 되며

동기임피던스의 식은 다음과 같습니다.

이제 동기 임피던스값이 구해졌으므로 전기자 저항값을 알면 동기 리엑턴스값을 알 수 있습니다.

전기자 저항값은 계자전류가 흐르지 않는 상태에서 외부 두 단자간의 저항을 측정하면 됩니다.

이 저항값은 두 상의 저항을 나타내므로 한상당 저항값은 이것의 반값을 취하면

됩니다. 실제적인 저항값은 이렇게 구해진 값보다 1.2에서 1.5배 큰 값을 취합니다.

이는 슬롯의 모양 등 여러가지 변수의 영향으로 실제 측정된 저항값보다 큰 값으로 영햐을

미치기 때문입니다.

단락비가 큰 기계의 특징으로는

① 동기임피던스가 작으며, 전압강하와 전압변동률이 작습니다.

② 전기자 반작용이 작고, 안정도가 향상되며 출력이 증가합니다.

③ 과부하 내량이 증가하여 선로의 충전용량이 증가합니다.

④ 철손이 증가하여 효율이 떨어지며 철이 많이 사용되어 철기계라고 합니다.

⑤ 공극이 크며 기계의 형태, 중량이 커집니다.

​

2. 단락비의 의미

​

동기발전기에서 무부하시험과 3상 단락시험을 통해 얻은

전류의 비를 '단락비'라고 한다.

여기서 무부하 시험과 3상 단락시험은 다음과 같다.

​

① 무부하시험

⊙ 동기발전기의 정격속도에서 무부하(부하 개방)로 운전하는 시험이다.

    무부하 시험을 통해 '정격전압(Vn)'을 발생시키는 여자(계자)전류를 구합니다.

    (이 무부하 시험을 통해 무부하 포화곡선을 얻을 수 있다)

② 단락시험

⊙ 동기발전기의 정격속도에서 단락상태로 운전하며 하는 시험이다.

    단락시험을 통해 '정격전류(In)'와 같은 크기의 단락전류를 발생시키는

    여자(계자)전류를 구합니다.

    (단락시험을 통해 단락곡선을 얻을 수 있습니다)

​

이 두가지 시험을 통해 얻은 각각의 여자전류로 단락비를 구합니다.

동기기에서 임피던스에 영향을 주는 것은 저항과 리엑턴스가 있으나

저항은 리엑턴스에 비해 크기가 매우 작아 무시해도 되므로

동기기에서는 Zs ≒ Xs 로 나타낼 수 있다.

또한 무부하(개방)회로 시험에는 동기리엑턴스(Xs)가 영향을 주고 단락시험에서는

동기임피던스(Zs)가 영향을 주나 이 두 영향은 같다고 가정할 수 있다.

​

한편 무부하시 정격전압을 발생시키는 계자전류는

단락시(동기리엑턴스만 영향)에 단락전류를 발생시키는 계자전류와 같다고 할 수 있다.

​

단락곡선은 전기자 반작용(리엑턴스)으로 직선형태를 취하므로 If" / If' = Is / In 이 된다.

​

동기임피던스 Zs ≒ 동기리엑턴스 Xs 라고 하였으므로 이를 Is / In 식에 대입을 하면

라고 할 수 있다.

따라서 단락비는 정격전류 대비 단락전류의 비율이며

동기임피던스 전압대비 정격전압의 비율이라고 말할 수 있다.

결국, 단락비는 동기임피던스와 반비례하게 된다.

단락비 관련 식을 정리하면

퍼센트 임피던스 식을 정리하면

3. 단락비의 특징

​

단락비가 '클 때'를 기준으로 정리해 보겠습니다.

​

들어가기 전에 아래 2가지를 기억해 주세요

① 단락비와 누설리엑턴스는 반비례 관계이다.

② 단락비가 큰 경우 철로 이루어진 기계, 돌극형을 사용합니다.

​

※ 단락비가 클 때 커진다.

⊙ 안정도가 커진다.

⊙ 계자 기자력이 커진다.

(철 기계이므로 계자전류가 크다 = 계자 기자력이 크다)

⊙ 선로의 충전용량이 커진다. - 선로 충전용량에 대한 여유분이 생긴다.

⊙ 철손이 커진다.

​

※ 단락비 클 때 작아진다.

⊙ 동기 임피던스가 작아진다.

⊙ 전기자 반작용이 작아진다.(누설리엑턴스가 작아진다=누설자속이 작다=전기자반작

용이 작다.

⊙ 전기자 기자력이 작아진다.

(전기자 반작용이 작아진다 = 전기자 기자력이 작아진다)

⊙ 전압 변동률이 작아진다.

(누설자속이 적다 = 전압변동이 작다)

⊙ 자기 여자현상이 줄어든다

(전압변동률이 작아진다 = 자기 여자 현상이 줄어든다)

​

【유도전동기 속도제어 '극수 변환법'】

유도전동기의 회전자의 회전속도는 다음 식으로 나타낼 수 있다.

유도전동기의 회전자의 속도는 1차측 회전자계의 회전속도 즉, 동기속도에

(1-S) 배를 한 속도로 회전하게 된다.

즉, 유도전동기 2차측 회전자 속도는 슬립(s), 주파수(f), 극수(p)에 의해 회전속도에

영향을 받게 되며 이들 요소를 제어하게 하게 되면 유도전동기의 회전속도를

제어할 수 있게 된다.

그중에서 극수(p)에 의한 속도제어법인 극수변환법을 알아 보자

​

1. 극수변환 속도제어 종류​

극수변환 속도제어는 2가지 방법으로 나눠진다.

​

(1) 논리극변환법

코일의 결선을 바꿔 줌으로서 고정자 권선의 극수를 바꿔주는 단순한 방법이다.

(고정자 권선의 극수가 높으면 속도가 느려진다)

극수변환법에서 주로 쓰는 방법으로 2:1 비율로만 속도제어가 가능하다.

​

예를 들어 4극기에서 2극기로, 8극기에서 4극기로

2:1비율로만 속도제어가 가능하다.

유도전동기 2차측의 회전자 속도는

에 따라서 극수가 높을 수록 회전자의 속도는 느려진다.

 ※ 극수와 회전수와 관계는 극수가 많으면 동일한 주파수를 내기 위해서

    많은 회전이 필요하지 않으므로 속도 속도가 낮아도 원하는 주파수를

    낼 수 있으므로 극수와 회전수는 반비례 관계에 있다고 한다.

    유도전동기의 회전자의 속도는 동기속도에 (1-S) 배를 한 것이 되므로

    극수가 많아져 동기속도가 낮아지면 유도전동기의 회전자 속도도

    낮아지게 된다.

​

(2) 다중권선법

극수가 다른 다중권선을 미리 감아두는 방법으로 2:1 뿐만아니라 여러비율로

변환이 가능하다.

그러나 고정자 권선이 커지고 비싸진다는 단점이 있다.

따라서 꼭 필요한 경우에 한정하여 사용된다.

​

2. 극수변환법 원리 (논리극 변환법)

극수변환법 중 논리극변환법의 원리를 확인해 보자 (2극기 ⇒ 4극기)

아래 그림은 4극기 유도전동기이다.

고정자에 3상 전원을 넣어주면 교류전원값 변화에 따라 회전자계가 형성된다.

이 자기장 변화에 따라 2차측 회전자가 힘을 받아 회전하게 된다.

​

아래 그림은 논리극변환법의 원리를 확인해 보기 위해

위의 4극기 유도전동기 3상중 한 상만 떼어낸 그림이다.

고정자인 a1, a1', a2, a2'에는 코일이 연결되어 있다.

이 때 고정자의 코일에 전류방향을 어떻게 해 주느냐에 따라서

2극기, 4극기로 변환이 가능하여 속도를 제어할 수 있다.

원리를 알기 위해서는 아래의 '암페어 오른나사 법칙'을 알아야 한다.

'암페어 오른나사 법칙'을 사용하면 전류 흐름에 따라 자기장의 방향이

어떻게 변하는지 알 수 있다.

먼저 2극기로 유도전동기의 속도를 빠르게 제어하고 싶으면 R2 점으로

전류를 흘리면 된다.

이 때

a1, a1' 에서 '암페어 오른나사 법칙'을 사용하면 자기장의 방향은 위로 향한다.

a2, a2' 에서 '암페어 오른나사 법칙'을 적용하면 자기장의 방향은 위로 향한다.

그러면 유도 전동기는 2극기의 형태가 되는 것을 알 수 있다.

​

다음으로 4극기로 변경하여 느리게 유도전동기를 속도제어하고 싶다면

R점으로 전류를 흘리지 않고 코일의 전류를 한방향으로 흘리면 된다.

이 때

a1, a1' 에서는 암페어의 오른나사 법칙에 따라 자기장이 아래로 향한다

a2, a2' 에서는 암페어의 오른나사 법칙에 따라 자기장이 위로 향한다.

두 자기장이 만나면서 오른쪽, 왼쪽 방향으로도 자기장이 형성된다.

그러면 결국 유도전동기는 4극기의 형태로 되는 것을 확인할 수 있다.

1. 유도 전동기의 속도와 슬립

▣ 유도전동기는 자석(회전자계)보다 원판이 속도가 늦어야 한다.

 ⊙ 유도전동기에는 3가지 속도가 있다.

   ◎ 동기속도 : 회전자기장의 회전속도

   ◎ 회전속도 : 회전자의 회전 속도

   ◎ 상대속도 : 회전자가 바라 본 회전자계의 속도 (원판에서 바라본 자속의 속도)

① 동기속도 Ns (1200 [rpm]이라 가정)

  ⊙ 회전 자계의 회전 속도로 입력속도라 한다. 일정한 속도로 정해져 있다.

     Ns (입력속도) = 1200[rpm], ⇒ N (출력속도) = 1140[rpm], SNs = 60[rpm]

​

② 실제속도 N : 1140 [rpm]

  ⊙ 회전자의 회전속도로서 출력속도라고 한다.

    ※ 발전기는 전기적 출력이 원칙, 전동기는 기계적 출력이 원칙이다.

​

③ 상대속도 SNs 60[rpm]

  ⊙ 회전자에서 본 동기속도를 말하며 손실속도라고 한다.

   ※ 동기속도와 실제속도가 같으면 출력이 나오지 않으므로 유도기에서는 약간의

      손실이 있어야만 회전력이 생긴다. 원판입장에서 보았을 때 동기속도가 도는

      상대적인 속도를 상대속도이다.

​

      1200 - 1140 = 60

      Ns - N = SNs

​

마찬가지로 유도전동기에서도 동기속도는 일정한데 부하가 증가하면 속도가 낮아진다.

따라서 부하가 낮아 지면 속도가 증가하고 부하가 없을 때(무부하시) 속도가 최고가 된다.

그러나 동기속도와 실제속도가 같아지면 회전력이 없어지므로 동기속도와 같을 수는 업쇼고 실제속도가 동기속도 보다는 약간 작아지게 된다.

​

⊙ 동기속도를 "1"로 보았을 때의 비율

⊙ 슬립(S)이 증가 ↑ ⇒ 회전속도 (N) 감소 ↓

    감소 ↓ ⇒ 회전속도 (N) 증가 ↑

⊙ 3상 유도 전동기는 동기속도 이하에서만 운전할 수 있다.

⊙ 3상 유도전동기는 슬립이 있을 때만 회전력을 받는다.

⊙ 부하가 증가하면 슬립이 증가한다.

​

2. 유도기 정지시, 운전시의 주파수 관계

​

1) 회전자가 정지했을 때

   회전자가 정지하고 있을 때는 고정자의 회전자계를 모두 고정자의 권선이

   끊어 주게 된다. 회전자계를 권선이 끊어주면 유기기전력이 발생하게 된다.

   이 때 발생하는 유기기전력을 식으로 나타내면 다음과 같다.

   ▣ 고정자 권선(1차) E1 = 4.44 k ω1 f1 N1 φ1

   ▣ 회전자 권선(2차) E2 = 4.44 k ω2 f2 N2 φ2

      f1 = f2

     φ1 = φ2

∵ 주파수 f 는 시간당 얼마나 회전하느냐가 결정하는 것이 아니라(×)

   시간당 자속을 얼마나 전기자가 끊어 주느냐가 결정하기 때문이다.​ ​

2) 회전자가 회전할 때

▣ 고정자 권선 (1차) : 60[Hz]

▣ 회전자 권선 (2차) : Sf2 = Sf1 [Hz]

▣ 고정자 권선(1차) : E1 = 4.44 k ω1 f1 N1 φ1

▣ 회전자 권선(2차) : E2 = 4.44 k ω2 Sf2 N2 φ2

   = S × 4.44 k ω2 f2 N2 φ2

   = S · E2

∵ 주파수 f 는 시간당 얼마나 회전하느냐가 결정하는 것이 아니라(×)

   시간당 자속을 얼마나 전기자가 끊어 주느냐가 결정하기 때문이다.

​

정지시 (회전 ×) Ns = 100[rpm]

N = 100[rpm] 이면 회전하지 못한다.

      회전시(기동시) Ns = 100[rpm] (회전자계 속도)

N = 0[rpm] (원판속도) , 정지시

f2 = 100[Hz]

S = 1 ※ 손실이 100[%] 효율 = 출력/입력 = 0

회전시(운전시) Ns = 100[rpm] Ns = 100[rpm] Ns = 100[rpm]

N = 90[rpm] N = 80[rpm] N = 70[rpm]

f2 = 10[Hz] f2 = 20[Hz] f2 = 30[Hz]

S = 0.1 S = 0.2 S = 0.3

​

【주파수 관계 】

① 정지시 : f1 = f2

   (회전자, 원판)

② 원판이 회전하더라도 1차 주파수는 불변 ⇒ f1 = 불변

③ 회전자 운전시(회전할 때) 2차 주파수는 1차 주파수의 슬립 S배이다.

​

【운전시 유기기전력 】

▣ 고정자 권선(1차) E1 = 4.44 k ω1 f1 N1 φ1

▣ 회전자 권선(2차) E2 = 4.44 k ω2 s f2 N2 φ2

=s 4.44 k ω2 f2 N2 φ2

= S E2

​ ∴ E2s = S E2 정지시 2차 기전력과 구별하기 위하여 E2s ​첨자 s를 붙인다.

​

★★ 종합정리

⊙ 정지시 2차 주파수 : f2 = f1

   운전시 2차 주파수 : Sf2 = Sf1

​

⊙ 정지시 2차 기전력 : E2

   운전시 2차 주파수 : SE2

​

⊙ 정지시 2차 리액턴스 : x2 = XL = 2πf2L

   운전시 2차 리액턴스 : Sx2 = SXL = 2πSf2L

​

⊙ 정지시 2차 저항 : r2 ⇒ R = ρ l/A

   운전시 2차 저항 : r2 ※ 저항은 R= ρ l/A 이므로 주파수와 관련이 없다.

   즉 저항은 회전속도와 관련이 없으므로 정지시나

   운전시 저항은 같다.

※ E2, f2는 고정시이며 이는 1차 E1, f1과 같다. 그런데 운전시를 구분하기 위해

   첨자 s를 붙여 E2s, f2s 로 운전시 2차 유기기전력과 주파수를 표시하게 된다.

​

ex1 : 슬립이 4[%]인 유도전동기에서 정지시 2차 한상의 전압이 150[V]일 때

      운전시 2차 한상의 전압은 ?

      운전시 E2 = SE2

      E2s = 0.04 × 150[V] = 6[V]

​

ex2 : 4극 60[Hz]의 3상 유도 전동기가 있다. 이 전동기가 정격시 1,725[rpm]으로

     회전할 경우, 2차 기전력의 주파수는 얼마인가?

     운전시 주파수 f2 = Sf2 = Sf1

     먼저 1차 주파수 f1을 구하면

​【 유도전동기의 슬립과 속도관계 】

동기속도는란?

⊙ 동기속도로 회전자계의 회전속도를 말한다.

3상 유도전동기의 경우 전동기의 전원의 3상 교류 전력을 이용하여 3상 교류 고정자

권선에 회전자기장을 만들고 있습니다.

동기화속도에 관한 식은 다음과 같습니다.

유도전동기의 슬립

​

⊙ 슬립이란?

슬립은 유도전동기의 동기속도 (Ns)에서 실제 회전속도(N)와의 차이의 비율,

즉 "상대회전속도 차이 (Ns-N)와 동기속도 (Ns)와의 비율을 말한다.

​

실제 회전속도는 예를 들면, 전동기가 정격속도로 회전하는 경우는 정격회전 속도를 말

합니다.

유도전동기의 경우 슬립이 있기 때문에 전동기는 동기속도로 회전하지 않고

동기화속도 보다 약간 늦은 속도로 회전합니다.

​

유도전동기와 달리 슬립이 없는 전동기를 동기전동기라고 하여

슬립이 없기 때문에 동기화속도와 실제 속도가 같습니다.

(동기전동기의 경우 슬립 S = 0)

​

슬립을 구하는 식은 다음과 같습니다.

1. 유도전동기 회전원리

​

▣ 유도 전동기는 아라고 원판의 회전원리에 따라 회전한다.

   아라고 원판 위 아래로 자석을 두고 이 자석을 회전시키면 자석을 회전하는 방향으로

   아라고 원판이 함께 회전하게 된다.

위 그림과 같이 자석을 시계방향으로 회전하면 아라고 원판도 시계방향으로

힘을 받아 회전하는 원리로 유도전동기도 회전을 하게 된다.

유도 전동기가 회전하려면 자석이 발생하는 자속을 원판이 끊어 주어 스스로 전자유도 전류

를 발생시켜야 원판이 힘을 받아 회전을 할 수 있다. 전류가 흐르기 위해서는 전자유도법칙

에 의한 기전력이 발생되어야 한다. 이를 위해서는 유도기는 우선 페러데이의 전자유도 법

칙에 따라 발전기의 역할을 하여 기전력을 발생시키고 전류를 흐르게 해야 한다.

​

⊙ 계자에서 자속이 발생되어야 한다.

⊙ 도체를 이용하여 자속을 끊어 기전력을 발생시켜야 한다.

​

즉 자석이 발생시킨 자속을 아라고 원판이 끊어 주어 기전력을 발생시켜야 한다.

위 그림을 보면 자석을 시계방향으로 회전을 하면 아라고 원판 즉, 도체는 반시계방향으로

운동하는 효과가 나타난다. 즉, 자석의 자계가 위에서 아래로 발생하는데 원판이 자속을

끊어 주므로 아라고 원판에 플레밍의 오른손 법칙에 따라 원판 중심으로 유기기전력이

발생하게 된다.

​

⊙ 플레밍의 오른손 법칙 : 기전력(전류) 방향

   ① 엄지(F) : 도체의 운동방향

   ② 검지(B) : 자속밀도 방향

   ③ 중지(I) : 전류의 방향

​

플레밍의 오른손 법칙에 따라 전류가 원판의 중심으로 흐르는 것을 알았다.

전류는 원판중심 방향으로 흐르고 자속밀도 방향은 위에서 아래로 발생하므로

플레밍의 왼손 법칙에 따라 원판은 시계방향으로 힘을 받게 됨을 알 수 있다.

⊙ 플레밍의 왼손 법칙 : 도체에 작용하는 힘의 방향

  ① 엄지(F) : 도체에 작용하는 힘의 방향

  ② 검지(B) : 자속밀도 방향

  ③ 중지(I) : 전류의 방향

​

※ 유도기는 스스로 유기기전력(전류)를 발생시켜야 하는데 유기기전력을 발생시키기 위해

서는 자속을 도체가 끊어 주어야 한다. 그런데 자속을 발생시키는 자석과 원판(도체)가

같은 속도로 회전을 하면 자속을 끊어 주지 못하므로 전류를 발생시킬 수 없고 결국에는

원판이 회전력을 발생시키지 못하게 된다.

​

유도전동기에서는 아라고 원판과 같이 자석을 회전시키지 않는다.

대신 3상 전류를 공급하여 회전하는 자계를 형성함으로서 자석이 회전하는 것과 같은

역할을 3상 전류가 하게 된다.

3상 교류 전력을 고정자에 공급을 하면 합성 자계가 시간의 흐름에 따라 회전하게 된다.

위 그림 1/4t에서는 a상은 나오는 방향이고 b,c상은 a상이 나오는 방향이므로 들어가는

방향이 된다. 그리고 a', b', c'는 각각 a, b,c상과 반대방향이 반대방향이 된다.

이를 연속하여 보면 아래 그림과 같이 회전자계가 합성되어 하나의 자극을 형성하게 되고

이 합성 회전자계가 회전하게 됨을 알 수 있다.

위 그림과 같이 3상 교류 전류는 합성 자속이 회전하고 있는 것을 볼 수 있다.

이 때 회전속도는 다음과 같다.

위 식에서 극수 P는 합성회전자계의 극수를 말한다. 위의 그림에서는 3상 전류가

Y결선으로 접속하였을 때 하나의 회전자계를 만드므로 자극은 N극, S극 이렇데

2개의 자극이 된다. 주파수는 60[Hz] 이므로 3상 전류가 만드는 회전자계의 회전

속도는 Ns = 120×60÷2 = 3600[rpm]이 된다.

​

2. 3상 유도전동기 구조 및 종류

​

▣ 3상 유도전동기의 구조를 다음 그림을 보며 알아 보자

3상 유도전동기에는 고정자에 3상 유도코일을 감아 회전자를 발생킨다.

회전자에는 회전자 도체가 있고 구리 막대(농형)나 권선(권선형)을 감는다.

3상 교류 전원은 회전자기장을 발생시키는데 이는 자석을 회전시키는 것과

같은 역할을 하게 된다.

원판이 자속을 끊어 주어야 원판이 힘을 받아 회전을 하게 된다.

이러한 역할을 하는 것이 회전자의 도체가 하게 된다.

원판은 회전자계와 같은 방향으로 회전을 하게 된다.

​

⊙ 1차 : 자석 : 회전자계

⊙ 2차 : 회전자 (원판) : 회전자 도체

​

▣ 유도 전동기는 회전자의 모양에 따라 농형유도전동기화 권선형 유도전동기로 나눈다.

​

【 농형유도전동기】

⊙ 고정자 1차 권선에 3상 교류 전류를 공급하면 회전자계가 형성된다.

   이 회전자계를 농형 2차 권선이 끊게 되면 유기기전력이 발생하게 되는데

   이 역할을 하는 것이 회전자의 구리막대이다.

   구리막대는 농형전동기를 기동할 때 사용하는 기동권선(제동권선)이다.

   ※ 제동권선 : 3상 동기 전동기 : 난조발생 방지

      3상 농형 유도전동기 : 기동토크 발생 (기동권선 역할)

      농형전동기에는 스큐슬롯 , 경사슬롯, 사슬롯, 사구를 사용한다.

​

▣ 스큐스롯을 사용하는 목적

◎ 고조파 제거 (기전력의 파형 개선)

◎ 고조파의 소음 발생 방지 (클로우링 현상 방지)

​

【 권선형유도전동기】

권선형 유도전동기는 회전내에 권선을 감은 형태의 전동기이다.

회전자 권선은 외부에 슬립링을 통해 외부의 가변저항과 연결된다.

※ R : 가변저항기의 저항, r2 : 회전자 내부에 있는 권선의 저항

​

고정자 1차 권선에 3상 교류 전류를 공급하면 회전자계가 발생하게 되고

이 회전자계를 끊어 주어 유도기전력을 발생시켜야 회전력을 얻을 수 있다.

권선형 유도 전동기는 농형과 달리 2차 저항을 가변할 수 있다.

​

⊙ 권선형 유도 전동기의 2차 저항을 가변하는 이유

   ◎ 기동할 때 기동전류를 제한하는 역할 R ↑ ⇒ I ↓

   ◎ 기동토크를 개선할 때 토크 τ ↑

   ◎ 속도 제어 (조정)​ ​​

※ 권선형 유도전동기는 회전자 권선에 전류가 흐르고 이 권선에는 저항이 브러쉬로

   연결되어 있으므로 브러쉬에 의한 손실, 그리고 전류 I​2R에 의한 손실이 발생하는

   등으로 효율이 좋지 않다. 따라서 권선형은 잘 사용되지 않는다.