1. 대전, 대전체, 전하량

※ 중성물체가 전기를 띠게 되는 현상을 대전이라 부른다.
중성물체는 양전하와 음전하가 같은 수가 있어서 전기를 띠지 않으나
음전하 중에 자유전자가 이동을 하여 양전하의 수와 음전하의 수가 달라졌을 때
전기를 띠게 되는데 이를 대전되었다고 한다.
▣ 대 전 : 중성물체가 전자의 이동으로 전기를 띠게 되는 현상
▣ 대전체 : 전기를 띠는 물체
① A 물체의 전기량 : + 1.602 × 10-19 × 3개 + Q [C]
① B 물체의 전기량 : - 1.602 × 10-19 × 3개 - Q [C]
※ 전기량을 전하량이라 부른다.
※ 양전하, 음전하의 수의 차이가 전기량이므로 전기를 띠게 되는 그 전하량의 차이,
전기를 띠게 하는 전하의 량을 전기량이라고 한다.
2. 정전유도 현상

▣ 중성물체 A에 대전체 B를 가까이 대면 성질이 다른 전하는 서로 흡인력이 발생하여
서로 당기게 되고 성질이 같은 전하는 서로 밀어내는 반발력이 작용하게 된다.
▣ 이러한 전하의 성질에 따라 A에 B와 가까운 쪽은 반대극성을 띠는 전하가
먼쪽은 같은 극성의 전하가 나타나게 된다.
3. 쿨룽의 법칙
▣ 정지된 두 전하사이에 작용하는 힘에 관한 법칙

⊙ 힘은 벡터량으로 크기와 방향을 가진다.
※ 같은 극성의 전하간에는 밀어내는 힘(반발력)으로 작용하고
다른 극성의 전하간에는 끌어 당기는 힘(흡인력)으로 작용한다.
【쿨룽의 법칙】
① 힘은 두 전하의 크기에 비례
② 힘은 두 전하사이의 거리의 제곱에 반비례
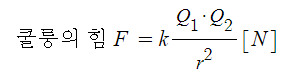
③ 쿨룽상수 : k
▣ 두 전하 Q1, Q2 가 놓여 있는 매질(공기, 기름...)에 의해 결정되는 계수

④ 유전율 : ε
▣ ε : 유전율 [F/m] : 전하를 유도하는 능력(성질)
▣ εo : 진공 또는 공기중의 유전율
⊙ εo : =8.855 × 10-12 [F/m]
⊙ εs : 비유전율 (비교 유전율)
※ 공기의 유전율을 기준으로 하여 다른 물질의 유전율을 비교한 값

※ 공기의 비유전율

【힘의 크기】
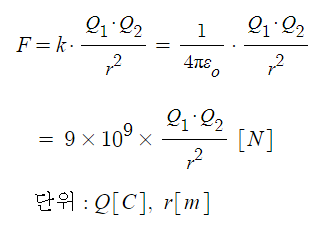
【종합정리】
▣ 힘 = 크기 + 방향
▣ 방향
⊙ 같은 극성의 전하

⊙ 다른 극성의 전하

결과 : 두 전하 사이에 작용하는 힘인 쿨룽의 힘은 두 전하를 연결하는
직선과 일치한다.
【쿨룽의 법칙, 예제 문제 풀이】
ex 1. 진공중에 두 전하가 일직선상에 놓여 있을 때 B전하에 작용하는 힘[N]은 ?
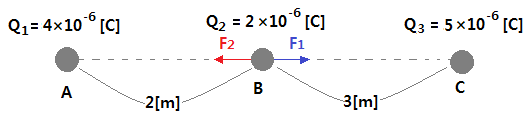
【문제풀이】
▣ A, B, C 전하는 모두 양전하이므로 서로간에 반발력이 작용한다.
▣ B전하에는 A전하의 반발력 F1, C전하의 반발력 F2가 동시에 작용한다.
▣ F1과 F2는 작용하는 힘의 방향이 반대이므로 양 힘의 합은 두 힘간의 차이다.
① 먼저 A전하에 의한 힘의 F1을 구해 보자.

② C전하에 의한 작용하는 힘 F2를 구해 보자.

③ B구에 작용하는 힘은 F1 - F2이다.

ex2 : 한변의 길이가 2[m]가 되는 정삼각형의 세정점 A, B, C에 10-4[C]의 전하가 있다.
이 때, 점 B에 작용하는 힘[N]은 ?
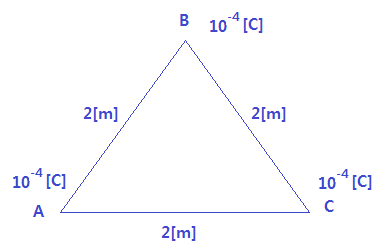
【문제풀이】
▣ 정삼각형의 각 정점에 크기가 같고 거리가 같은 전하가 놓여 있으므로 작용하는 힘은
같으나 방향이 다르므로 작용하는 힘의 합은 벡터합으로 구해야 한다.
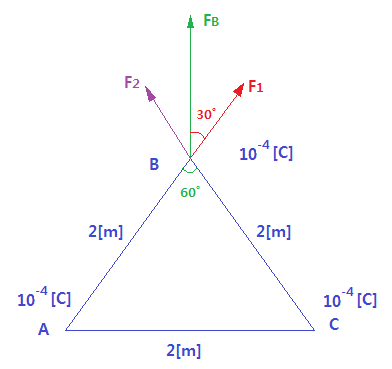
① A에 의해 작용하는 힘 F1 과 B에 의해 작용하는 힘 F2를 구해 보자.

※ 두 전하간에 작용하는 힘은 쿨룽의 법칙에 의하여 계산할 수 있다.
여기서 9 × 10^9의 공기중의 유전율로 나눈 값이다.
▣ 두 힘의 합은 벡터 합으로 구한다.

※ 벡터의 합은 코사인 법칙에 의하여 계산할 수도 있고 삼각함수와 평행사변형에
의한 방법 등을 이용하여 계산할 수 있다.
'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
|---|---|
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
| 정전계, 전자유도, 쿨룽의 법칙 - 전자기 (0) | 2021.08.25 |
| 벡터의 정의, 표현, 가감연산, 내적, 외적 (2) | 2021.08.25 |
