예제1 : V = 3x2y - y3z2 일 때 grad 의 점 (-1, -2, -1)에서의 값은 ?
※ 전위 경도를 구하라는 문제로서 grad는 편미분을 하라는 의미이다.
따라서 먼저 전위 V에 대하여 편미분을 하게 되고
편미분을 하고 난 후에 한점의 좌표값을 넣어 계산을 하면 된다.

▣ 전위 V에 대하여 편미분을 하였다. 전위 V를 x, y, z 축에 대하여 편미분을 하였다.

※ 위에서 편미분한 식에 대하여 점의 좌표값을 대입하여 최종값을 산정하였다.
예제2 : 전위함수 V = 2x+5yz+3 일 때 점 (2,1,0) 에서의 전계의 세기는 ?
※ 먼저 숙지해야 할 사항 : 전계의 세기 " E = - grad V " 이다.
전계의 세기는 마이너스(-) 전위경도 이므로 전위함수에 대하여
우선 편미분을 하게 된다. grad는 경도, 기울기를 의미하며 연산자는
편미분 연산자 즉 ▽을 적용하게 된다.

【 벡터의 발산 】 ⇒ div, ▽ · (나블라 도트)
▣ 발산은 기호로 div 즉 diversions를 말하며 연산기호는 ▽· 이다.
발산은 편미분 연산자와 내적의 합성으로 결과값은 스칼라값이 된다.
▣ 발산의 계산, 산정방법
① 어떤 벡터 A가 있을 때 div A (▽·) 가 있을 때는
② 단위 체적당 발산하는 전기력선의 수를 계산하는 것임
A = Axi + Ayj + Azk 에 대하여 발산(div A), ▽· 를 구하라.

※ ▽· 는 계산 대상과 편미분 연산자를 내적하라는 의미로 보면 된다.
※ · (도트) 내적은 같은 성분끼리의 내적만 존재한다.

※ 내적의 곱은 스칼라값으로 나온다.
⇒ i, j, k 가 없다.
예제1. 벡터 A = x2i + y2j + z2k 일 때 점 (1,2,3) 에서 발산을 구하시오.
※ 발산 : div = ▽· ⇒ ▽ · A
▣ 발산 div를 구하라는 말은 계산 대상과 편미분 연산자를 내적하라는 말이다.
따라서 편미분 연산자 ▽과 벡터 A를 내적하게 된다.

예제2. 전계 E = 3x2i + 2xy2j + x2yzk 일 때 div E를 구하라.
div = 발산 = ▽ · E
▣ 전계의 발산을 구하는 것은 전계를 편미분 연산자 ▽와 내적하라는 말이다.

※ 한점이 주어지면 점 (1,2,3)을 위 식에 넣어서 계산하면 된다.
【 벡터의 회전 】 rot, curl ⇒ ▽ × (나블라 크로스)
① 어떤 벡터 A = Axi + Ayj + Azk 일 때
② rot A = curl A = ▽ × A
※ 외적의 결과는 벡터이다. i, j, k 가 있어야 한다.

rot, curl는 벡터의 회전값을 구하는 것으로 이는 벡터의 외적값을 구하는 것이다.
외적은 값은 성분끼리의 값은 "0"이므로 자신과 같은 성분값은 계산하지 않고
자신과 다른 성분의 값으로 연산을 하게 된다. x축 성분의 값을 계산하는 경우에는
rot와 curl 값을 구하는 방법은 ①방향으로 곱한 다음에 이를 ②방향으로 곱한 값을
빼주는 방식을 산정을 하게 된다.
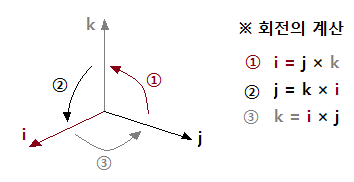
예제 1. 벡터 A = xyi + yzj + zxk 일 때 점 (4, 5, 3)에서의 ▽×A를 구하시오.
▽ × 는 curl, rot 를 구하라는 말로 이는 편미분 연산자 ▽과 계산 대상자를
외적하라는 말이다. 외적을 할 때에는 성분이 같은 경우에는 결과 값이
'0'이 되므로 성분이 다른 값을 계산하게 된다.
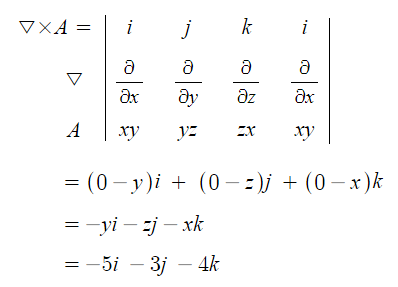
예제2. 벡터 A = xyz2i + xyzj + x2yzk 일 때 rot A를 구하면 ?
※ rot A = ▽ × A
rot 을 구하라는 의미는 편미분 연산자 ▽과 계산 대상을 벡터 외적하라는 의미이다.
외적을 할 때에는 성분이 같은 경우에는 결과 값이 '0'이 되므로 성분이 다른 값을
계산하게 되고 결과값은 벡터로 표시되게 된다.
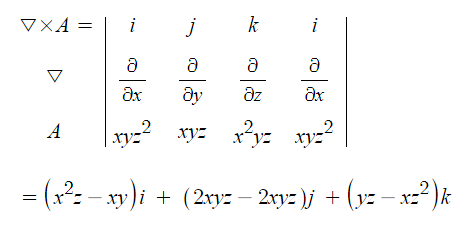
【 종합정리 】
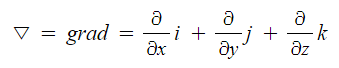
※ ▽ : 나블라, 델 - 편미분하라.
div 발산 = ▽· ⇒ 같은 성분 끼리만 내적한다.
※ i, j, k 가 없다.
rot = curl = ▽ × ⇒ 다른 성분끼리 외적한다.
※ i, j, k 가 붙는다.
'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 전속과 전속밀도 (0) | 2021.11.11 |
|---|---|
| 유전율과 전계의 세기 (0) | 2021.11.11 |
| 전자기학 - 전기력선, 등전위면, 도체, 벡터 미분 (0) | 2021.10.29 |
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
