아낌없이 주는 나무

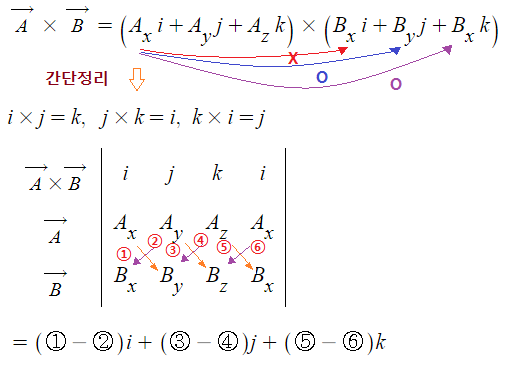
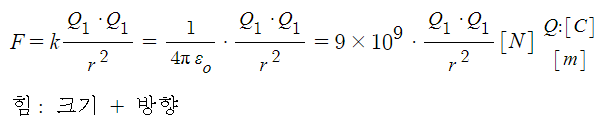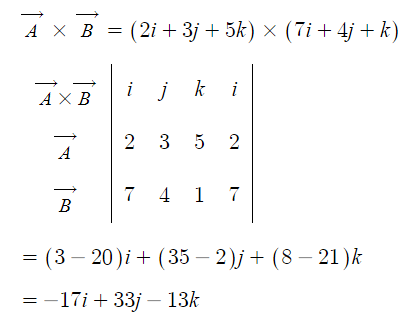▣ 정전용량 [C] - 선로정수

​

선로정수중에서 정전용량에 대하여 알아 봅시다.

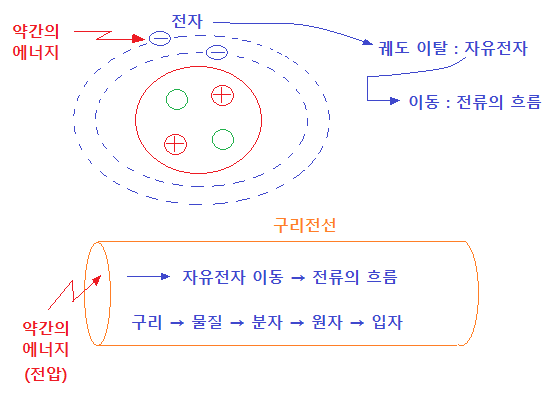
전력계통에서 정전용량 [C]는 콘덴서와 관련이 있습니다.

여기서 콘덴서란 콘덴서 제품을 말하는 것이라기 보다는 콘덴서 역할을 하는

것들의 작용에 의한 것입니다.

콘덴서는 아래 그림과 같이 도체사이에 절연물질이 있는 것입니다.

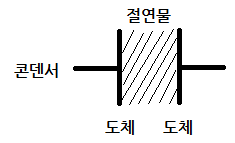
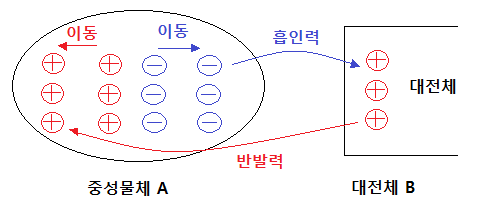
전력계통에서는 정전용량은 2가지 경우에 나타납니다.

선로와 대지사이는 두 도체 사이에 절연물인 공기가 있어 콘덴서 역할을 하고

전선과 전선사이에도 두 도체사이에 절연물인 공기가 있으므로 콘덴서 역할을 하여

각각 정전용량이 발생하게 됩니다.

​

⊙ 정전용량도 인덕턴스와 마찬가지로 3가지가 있습니다.

자기(대지)용량, 상호(선간), 작용(합성)정전용량이 있습니다.

각각의 정정용량을 그림으로 나타내면 다음과 같습니다

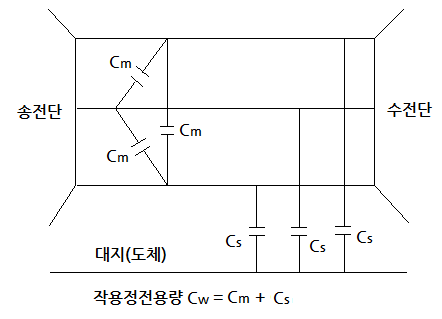
1. 전기공급방식에 따른 작용정전용량

▣ 송전계통에서 작용정전용량은 전기공급방식에 따라 산정식이 달라집니다.

    단상의 경우에는 상호정전용량을 2배, 3상은 3배를 하며 이것은 한상분의 정전용량입

    니다.

⊙ 단상 : 작용 정전용량 Cw = Cs + 2 Cm

⊙ 3상 : 작용 정전용량 Cw = Cs + 3 Cm

​

[단상2선식]

⊙ 상호정전용량은 콘덴서가 직렬연결과 같습니다. (저항의 병렬연결)

    따라서 합성 정전용량인 작용정전용량은 다음과 같습니다.

※ 개인적인 생각으로는 상호정전용량인 Cm은 a선의 전압에 의한 Cm과 b선의 전압에

   의한 Cm의 합이므로 2Cm이 되어야 하는 것이 아닌가 생각한다. (이렇게 외우고 이해

   하는 것이 쉽지 않을까 생각한다.)

​

[3상 3선식]

▣ 3상 3선식 송전선로에서 상호정전용량 Cm은 △결선에 해당하므로 각 상의 상호정전

   용량을 각 상의 정전용량으로 나누기 위해 △결선을 Y결선으로 등가변환한다.

   △결선에서 Y결선으로 등가변환하면 저항(R), 리액턴스(x), 임피던스(Z)는 1/3배로

   줄어든다. 따라서 △결선의 Cm은 Y결선의 3Cm과 같고 한상의 상호정전용량은

   3Cm이 된다.

※ 3상의 경우에도 한상에 걸리는 상호정전용량 Cm은 자신의 전압에 의한 상호정전용

   량Cm, 다른 2선에 의한 전압에 의한 상호정전용량을 합하여야 하므로 3Cm이다

   이렇게 이해하는 것이 암기하기도 쉬운 것 같다.

​

2. 전선의 종류에 따른 작용정전용량

3. 충전전류 (앞선전류 = 진상전류)

​

▣ 충전전류 : 정전용량(콘덴서)에 흐르는 전류 : 한상분을 말함

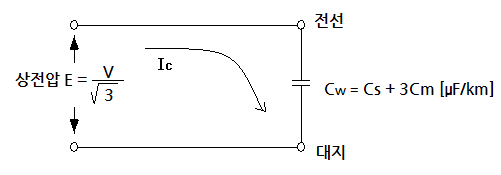
▣ 송전선과 대지간에는 대지전압이 걸리게 되며 이 전압에 의하여 정전용량이 발생한다.

   송전선과 대지간에는 전압차가 있기 때문에 전류가 흐르게 되는 이를 충전전류라 한다.

⊙ 충전전류의 구하는 식은 전압을 저항 즉 작용정전용량으로 나누어 산정한다.

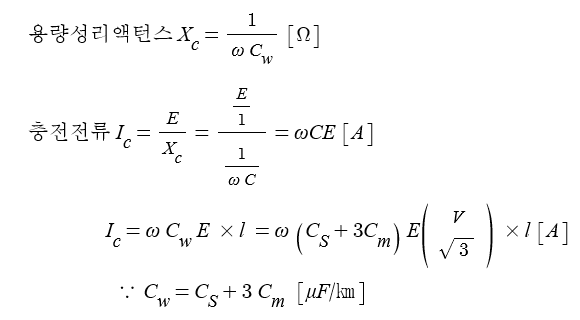
※ 정태시 : 고장이 나지 않은 정상적인 운전상태

​

4. 충전용량 (진상용량)

​

※ 콘덴서는 양 극간 전압을 모으고, 에너지를 충전한다.

​

▣ 충전용량은 정전용량(C)을 말하며 쉽게 말하면 콘덴서용량이라 할 수 있다.

    송전계통의 충전용량 즉 정전용량을 말할 때는 3상 전체값을 일컬는다.

   ※ 변압기 용량을 [kVA] 로 나타 내듯이 용량이란 말이 나오면

      피상용량[VA] = 전압 × 전류 를 말한다.

    Qc = 3 E × Ic = 3 E × ω CE = 3 ω CE2 = ω CV2 [VA] × 10-3 [kVA]

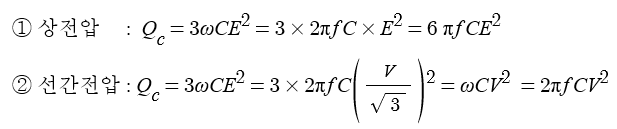
5. 누설컨덕턴스

​

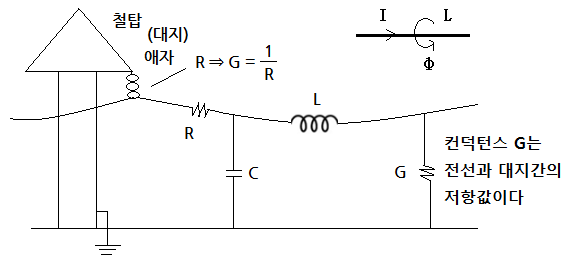
▣ 송전선로에서 컨덕턴스는 누설저항값이다. 누설저항으로는 애자표면의 누설전류가

    대부분이므로 그 값은 대단히 크고 그 역수인 누설컨덕턴스는 대단히 작아서 선로

    정수로는 실용상 고려할 필요가 적다. 따라서 누설컨덕턴스는 무시하는 것이 보통이다.

저항 (R) : 송전계통에서 저항은 전류가 흐르지 않아도 전선이 주어지면 정해진다.

인덕턴스(L) : 송전계통의 전선에 전류가 흐르면 그 전선 주위에 자속이 발생하고

발생된 자속에 의하여 유도성 리액턴스가 발생한다.

정전용량(C) : 송전계통의 전선에 전압이 걸리면 선로와 대지간, 그리고 선로 상호

간에 정전용량이 발생한다.

누설컨덕턴스 (G) : 송전선로에서 컨덕턴스는 누설저항값이다. 누설저항으로는 애자표면

의 누설전류가 대부분이므로 그 값은 대단히 크고 그 역수인 누설컨덕턴스는

대단히 작아서 선로정수로는 실용상 고려할 필요가 적다. 따라서 누설컨덕턴스

는 무시하는 것이 보통이다.

​

⊙ 누설컨덕턴스는 애자를 통하여 전류가 새는 것을 말하는 것으로 애자는 철탑을 통하여

    대지로 연결된다. 그러므로 송전계통에서 누설컨덕턴스는 전선과 대지간의 저항값이

    라고 할 수 있다.

​

▣ 이렇게 하여 송전선로가 주어지면 전력의 송전에 영향을 주는 선로정수 R, L, C,G가

    정해지고 얼마나 영향을 주는지 그 영향정도를 선로정수라고 한다.

⊙ 이들 선로정수중 저항(R)과 인덕턴스 (L)은 전선에서 발생하므로 R과 L은 직렬로

    연결되어 있다고 볼 수 있고

⊙ 정전용량과 누설컨덕턴스는 전선과 대지간에 발생하는 것으로 병렬로 연결되어 있다

    고 볼 수 있다.

​

이러한 4가지 선로정수를 종합하여 등가회로로 구성하면 다음 그림과 같다.

저항과 인덕턴스는 전선에 의해 발생하므로 직렬로 연결되고 합하여 선로임피던스를

구성한다. 정전용량과 누설컨덕턴스는 전선과 대지간에 발생하므로 선로에는 병렬연결

개념으로 어드미턴스를 구성한다. 정전용량과 인턱턴스는 송전로 1[km]를 단위로 하며

이에 따라 합성 등가회로는 1[km]를 단위로 구성되고 전선로의 길이가 100[km]라면

이러한 등가회로가 100개가 있는 것과 마찬가지 인데 이를 종합하여 분포정수회로라고

부른다. 이들 [km]당 선로정수와 100[km]의 합성선로 정수의 산정식은 다음과 같다.

이들 송전계통의 선로정수를 하나의 등가회로로 나타내는 것이 집중정수회로이며

이는 아래 그림과 같다.

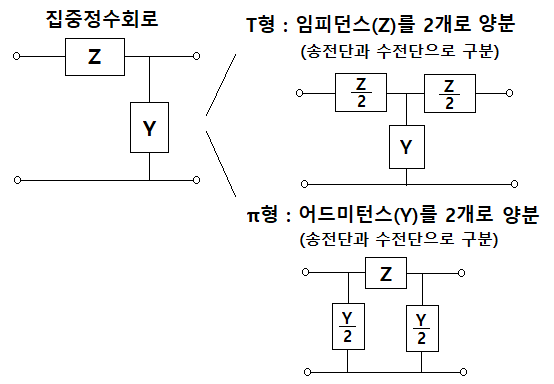
이 집중정수회를 분석하기 위하여

임피던스(Z)를 송전단과 수전단의 둘로 양분하여 분석하는 것이 4단자 정수 T형이고

어드미턴스(Y)를 송전단과 수전단 둘로 양분하여 분석하는 것이 4단자 정수 π형이다.

​

【정전계】

▣ 전계란 어떤 물질이 대전이 되었을 때 전기의 성질을 띠게 되는데

    이 대전체는 공간상에 전기적인 힘, 영향을 미치게 된다. 이렇게

    공간상에 전기적인 영향이 나타나는 현상을 전계라고 한다.

    이러한 전계중에서 전하가 정지하고 있는 상태의 전계를 정전계라 한다.

  ⊙ 전하(양성자, 전자)가 정지하고 있을 때의 전계

★⊙ 전계 에너지가 최소로 되는 전하분포의 전계

​

【물질과 전계】

▣ 물질 → 분자 → 원자 → 입자

⊙ 물 → H2O → H(수소) + O(산소) - 물질의 최소 단위

⊙ 물질은 분자로 이루어져 있으며 이 분자는 다시 원자로 구성되어 있고

    원자는 다시 입자로 구성되어 있다. 이중 입자에 의하여 전기적인

    성질을 띠게 되고 입자는 다시 +성질을 띠는 양성자와 - 성질을 띠는

    음전하로 나뉘게 된다.

▣ 전하의 전기량 : ± 1.602 × 10-19 [C]

※ 전자가 원자핵 즉 양성자와 가까이 있게 되면 전자와 양성자간 작용하는 전기적 힘이

   세므로 전자는 양성자에 구속되기 쉽고 만약 전자가 양성자와 멀리 떨어진 경우에는

   전자와 양성자간 전기적 힘이 상대적으로 작으므로 이 전자에 약간의 외부적인 힘을

   가하면 전자가 양성자의 구속에서 벗어나 궤도를 이탈하는 경우가 있다. 이를 자유전자

   라고 하며 이 자유전자의 이동이 전류의 흐름으로 나타난다. 구리와 같은 도체는 이런

   자유전자의 흐름이 양호한 물질이다.

가. 대전, 대전체, 전하량

▣ 대전 : 중성물체가 전하의 이동으로 전기를 띠는 현상

▣ 대전체 : 전기를 띠는 물체

   ⊙ A 물체의 전기량 : +1.602 × 10-19 [C] × 3개

   ⊙ B 물체의 전기량 : -1.602 × 10-19 [C] × 3개

     ⇒ 전기량 : 전하량 (Q [C])

 ※ +성질의 띠는 양전하와 -성질을 띠는 음전하의 전기량은 동일하다.

    특정물질에서 양전하의 수와 음전하의 수가 동일하다면 이 물질은

    동일한 +전기량과 -전기량을 갖게 되므로 전기적으로 중성이 되며

    자유전자가 이동하여 양전하와 음전하의 수가 달라지면 + 혹은 -의

    전기적 성질을 띠게 된다. 이를 대전되었다고 한다.

​

나. 정전유도 현상

▣ 정전유도 현상

   ⊙ 중성물체 A에 대전체 B를 접근시키게 되면 A에 B와 가까운 쪽은 반대극성의 전하가

       먼쪽은 같은 극성의 전하가 나타나는 현상

   ⊙ 이는 +성질을 띠는 양전하와 양성전하는 서로 밀어내는(반발력)이 작용하고 +성질을 띠는

       양전하와 -성질을 띠는 음전하는 각각 당기는 힘(흡인력)이 작용하여 +성질이 띠는 대전체를

       중성물질에 가까이 하면 양전하는 밀어내고 음전하는 당기게 되어 대전체에 가까운 곳은

       음전하가 몰리게 되고 대전체에서 먼 곳은 양전하가 몰리게 되어 중성물질의 표면에

       전기적 성질을 띠는 대전현상이 발생하게 된다.

​

다. 쿨룽의 법칙

  ▣ 쿨룽의 법칙

    ⊙ 정지된 두 전하 사이에 작용하는 힘에 관한 법칙

     ⇒ 정지된 두 전하 : 정전하, 힘 : 벡터 : ① 크기, ② 방향

【쿨룽의 법칙】

  ① 힘 : 두 전하의 크기에 비례

  ② 힘은 두 전하 사이의 거리의 제곱에 반비례

【유전율】

   ε : 유전율 [F/m], 전하를 유도하는 능력

   εo : 진공 또는 공기중의 유전율 εo = 8.855 × 10-12 [F/m]

   εs : 비유전율(비교) : 공기의 유전율을 기준으로 다른 물질의 유전율을 비교한 값

【힘의 크기】

【방향】

▣ 같은 극성 : 반발력 다른 극성 : 흡인력

   [결과] 두 전하에 작용하는 힘의 방향은 두 전하를 연결하는 직선과 일치

​

[예제1] Q1= 4 ×10-6, Q2 = 2×10-6, Q3 = 5 × 10-6 의 3개의 구전하가

진공중에 일직선으로 놓여 있을 때 B구에 작용하는 힘은 [N]은 ?

[예제] 한변의 길이가 2[m]가 되는 정삼각형의 3정점 A, B, C에 10-4의 전하가 있다.

        점 B에 작용하는 힘[N]은 ?

​

【 벡터의 정의, 표현 】

1. 벡터와 스칼라

​

가. 물리량을 나타내는 방법

  ⊙ 스칼라 : 크기만으로 양을 표현하는 것 (길이, 무게, 속력 등)

             ※ 스칼라 값은 단위로 쓰이는 물리량을 나나태는 경우가 많다.

  ⊙ 벡터 : 크기와 방향으로 양을 표현하는 것.

            ※ 대부분의 물리량은 크기와 방향을 갖고 있다.

               일반적인 물리량은 벡터라고 보면 된다.

​

나. 벡터의 표현 : 화살표로 표현 (→)

  ▣ 벡터는 시점에서 종점을 잇는 직선으로 표시하며 시점에서 종점으로

      방향을 나타내는 화살표로 표시하게 된다. 벡터는 크기와 방향을 갖고 있으므로

      벡터의 크기는 직선의 길이로 나타내며 방향을 화살표 방향으로 표기하게 된다.

      방향을 기준방향을 기준으로 편각을 이용하여 표기하기도 한다.

다. 직각 좌표 (공간좌표)

▣ 공간상에서 임의의 한점을 표현

  ※ 직각 좌표계는 공간상의 위치나 방향 등을 수치로 표시하여

     이를 합산하거나 연산을 할 수 있도록 하는 중요한 개념이다.

▣ x, y, z 축을 이용

① 좌표점을 이용하는 방법

② 수식화하는 방법

​

1) 좌표점을 이용하는 방법

▣ 벡터의 표현 : (종점좌표) - (시점좌표)

⊙ 벡터의 표현 (3, 4, 5) -(0, 0, 0) = (3, 4, 5)

   ex : A점 (1,2,1), B점 (3,4,5)일 때 A점에서 B점으로 향하는 벡터의 표현은 ?

   (3,4,5) - (1,2,1) = (2, 2, 4)

 ※ 위에서 말한 바와 같이 좌표점을 이용하게 되면 벡터의 값 즉, 크기와 방향을

    수치화할 수 있고 이는 벡터와 방향을 모두 수식에 의해 연산할 수 있다는

    장점이 있다.

​

2. 수식화하는 방법

가. 단위 벡터

▣ 단위벡터 : 크기는 "1"이면서 방향만을 나타내는 벡터

                  벡터를 표현하는 방법

   ※ 단위는 "1"을 나타내며 벡터 뿐만 아니라 다른 물리량을 나타낼 때도

      단위는 각각의 물리량을 비교하기 위한 척도이며 각각의 물리량을

      나타내는 기본이 된다.

[단위벡터의 정의]

   ① 크기가 "1"이면서 방향만을 나타내는 벡터

   ② 표현하는 방법 : ao, bo, co....

나. 기본벡터

① 정의 : 각 축(x, y, z)상에 존재하는 단위 벡터

기본벡터 표현방법 : i, j , k

​

[기본벡터 정리]

▣ 정의 : 각 축상에 (x,y,z)에 존재하는 단위벡터

▣ 기호 : i(x축), j(y축), k(z축)

▣ 기본벡터도 단위벡터에 포함이 된다.

▣ 기본벡터도 좌표점으로 표현이 가능한다.

     i(1,0,0), j(0,1,0), k(0,0,1)

​

3. 벡터를 수식화하는 방법

① 벡터의 표현

② 벡터의 크기

ex : 좌표점이 (2,5,6)인 벡터 (A)의 표현, 크기 및 단위벡터는 ?

4. 벡터의 계산

​

가. 가감법

① 대수학적 방법 : 수식적으로 계산한다.

⇒ 같은 성분들 끼리 가감한다.

예제 ex : A벡터와 B벡터의 합과 차는?

나. 기하학적 방법 (도형으로 구하는 방법)

ex : 두변의 크기가 같고 편각 Θ=60˚ 인 경우

 ▣ 두 벡터가 있고 이들 사이에 사잇각을 알게 되면 두 벡터의 합은 cos법칙에 의하여

     계산할 수가 있다.  

  ⊙ 특수각은 sin, cos 값이 실수로 나타나는 값으로 30˚, 45˚, 60˚ 등을 말한다.  

▣ 두변의 크기(길이)가 같고 이루는 각도가 120˚ 인 경우

다. 뺄셈 (차감)

​

▣ A-B의 경우 ⇒ A+(-B), "-" 는 방향

⊙ B → A, B에서 A로 향하는 벡터

 ※ 벡터의 뺄셈은 빼고자 하는 벡터의 반대 부호값과 뺄 대상 벡터의 합으로 구할 수 있다.

    벡터는 평행이동하여도 그 값이 변하지 않으므로 결국 벡터의 뺄셈은 빼고자 하는

    벡터의 종점에서 빼는 대상 벡터의 종점을 잇는 선으로 표기할 수 있다.

▣ B-A의 경우 ⇒ B+(-A)

⊙ A → B, A에서 B로 향하는 벡터

​

【벡터의 연산, 내적, 외적 】

1. 벡터의 곱셈 (내적)

​▣ 벡터 곱의 결과

 ⊙ 스칼라 (크기) ⇒ 내적

   - 벡터를 내적을 하게 되면 그 값은 스칼라 값으로 나타난다.

 ⊙ 벡터 (크기+방향) ⇒ 외적

   - 벡터를 외적하게 되면 그 값은 벡터값으로 표현된다. 

​

가. 벡터의 내적

1) Dot 곱 (표현), 스칼라곱 (결과) ⇒ 크기

2) 벡터 · 벡터 = 스칼라

나. 기본벡터의 내적

 ▣ 각 축(x,y,z) 상의 단위 벡터 i(x), j(y), k(z)

▣ 내적은 같은 성분끼리의 내적은 성립

▣ 다른 성분과의 내적은 성립하지 않는다.

    ※ 결과값에 i, j, k가 붙지 않는다.

        크기만 있고 방향성분은 없다. 결과값은 스칼라값이다.

​

다. 벡터의 내적 계산

라. 두벡터가 이루는 각도 계산 (무조건 벡터 내적)

ex : 벡터 A = -7 i - j 이고 벡터 B = -3i - 4j 일 때 두 벡터가 이루는 각도는 ?

라. 두 벡터의 수직조건 : 벡터 내적의 결과가 "0"이 되는 조건

【 암페어의 오른 나사 법칙과 벡터의 외적 】

1. 암페어 오른 나사 법칙

▣ 전류( I )에 대한 자속( φ )의 방향 결정

 ※ 도체에 전류가 흐르면 그 주위에는 회전하는 자계가 형성하게 되는데

    이 때 전류의 흐름과 자계의 방향을 확인하는 방법으로 암페어의 오른 나사의 법칙을

    사용한다.

▣ 전류( I ) ∝ 자속( φ ) ⇒ 비례 관계

【 자석에 의한 자속 】

​

【 원형코일 전류와 자속 】

▣ 전자석 : 철심 + 코일 = 자극에서의 자속 방향

2. 벡터의 외적

▣ Cross 곱 또는 벡터곱

⊙ 표현 : X, 결과 (벡터곱) : 크기와 방향

⊙ A · B ⇒ 스칼라 (크기)

⊙ A × B ⇒ 벡터 (크기 + 방향)

※ 벡터 × 벡터 = 벡터

2) 크기 : 두벡터를 두변으로 하는 평행사변형 면적

3) 방향 : A에서 B로 오른 나사를 돌릴 때 나사의 진행방향

[방향]

① A × B : A에서 B로 오른 나사를 돌리는 방향

② 면적 : 두벡터가 이루는 평행사변형의 면적

가. 기본벡터의 외적

▣ 각 축 (x, y, z) 상의 단위 벡터 ⇒ i, j, k

【 기본벡터의 외적 정리 】

① 같은 성분 끼리의 외적은 불성립 ×

② 다른 성분 끼리의 외적은 성립 O

​

나. 두 벡터의 외적

예제)

예제 2 : A=10i-10j+5k, B = 4i-2j+5k가 어떤 삼각형의 두변을 표시하는 벡터이다.

이 삼각형의 면적은 ?