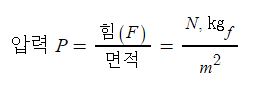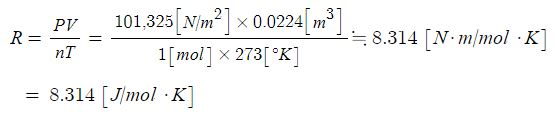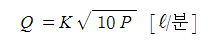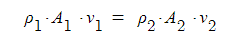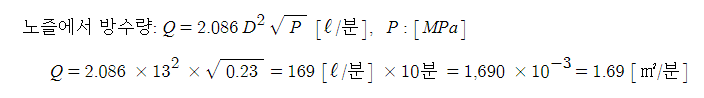1. 질량(mass : M, m)이란 무엇인가 ?
▣ 질량(mass)이란 특정 공간에 어떤 속성의 물질이 얼마만큼 있는지를 나타내는 물리적인 양을 말하며 질량이란 말에는
밀도와 비슷한 개념이 포함되어 있고 뉴턴의 운동법칙에 의한 어떤 물체에 힘을 가할 때 발생하는 가속도에 대한 저항
의 정도, 또는 관성의 정도를 의미하기도 한다. 따라서 밀도를 측정한다는 것은 어떤 부피내에 어떤 특성의 물질이 있는
지 측정하는 것이 되고 또한 측정 대상의 물체를 구성하는 원자의 총수와 밀도, 유형 등을 알 수 있게 된다. 질량은 어떤
물체의 구성하는 물질의 물리적인 양으로 물질의 고유한 성질을 나타내는 것으로 벡터가 아닌 스칼라이며 어느 공간에
있더라도 동일하므로 중력을 영향을 받지 아니한다. 또한 측정 대상 물체가 존재하는 한 질량이 영(zero)가 될 수 없고
기호로는 M,m을 단위로는 [kg]과 [g]을 쓴다.
2. 무게 (weight, W)란 무엇인가 ?
▣ 무게란 어떤 물체가 받는 중력의 힘을 말한다. 즉, 어떤 물체가 지구의 중력에 의한 힘을 받아 그 물체가 얼마 만큼의
힘으로 지구중심부를 향해 끌어 당겨지는지를 나타낸다. 따라서 뉴턴의 운동법칙에서 나오는 힘으로 표현되며 질량(m)
과 중력가속도(g)의 곱으로 나타낸다. 중력가속도는 크기와 방향을 가지는 벡터(vector)이고 지면에 수직으로 작용하며
중력가속도는 위치에 따라 변하므로 동일한 물체라도 환경에 따라 무게가 달라질 수 있다. 무게는 질량에 작용하는
중력의 힘이라고도 할 수 있으므로 동일한 중력가속도가 작용하는 곳에서는 질량에 따라 무게가 결정되므로 무게도
궁국적으로는 질량의 척도라고 할 수 있다. 무게의 단위는 힘의 단위인 N[㎏·m/s2]과 [㎏f]를 쓴다.
3. 밀도란 무엇인가 ?
▣ 밀도(density)는 질량의 개념을 물리량 계산에 적용하기 위해서 도출된 개념으로 동일한 물질을 기준으로 하여 단위
체적(부피)당 질량으로 정의되고, 비질량(specific-mass) 이라고도 한다. 또한 밀도는 단위 가속도 대비 작용하는 힘에
저항하는 관성의 정도로 표현하기도 한다.
따라서 밀도는 어떤 물질의 질량이 m, 부피가 V인 경우 수식으로는 밀도(ρ) = 질량 (m) / 부피 (V)로 나타낸다. 국제 단위
계의 단위로는 [㎏/㎥], [g/㎤] 이다. 또한 가속도 대비 작용하는 힘에 대한 관성의 정도를 나타내는
밀도 (ρ) = 힘(F) / 가속도 (a)로도 나타내며 이를 풀어 보면 ρ = N /(m/s2) =(N·s2)/m으로도 나타낼 수 있다.
하지만 이 단위로는 밀도 값이 보통 한두 자리로 나오기 때문에 [g/㎤] 단위를 사용하기도 한다. 대표적인 액체 유체인
물 (Water)의 밀도는 4[℃]일 때 1 [g/㎤] = 1,000 [㎏/㎥]이다.

▣ 액체 비중의 기준이 되는 물(H2O)의 밀도는 다음과 같다.
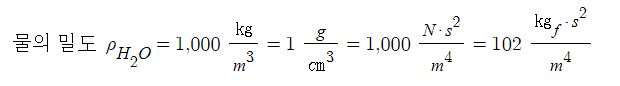
4. 비중량(specific weight)이란 무엇인가 ?
▣ 비중량은 밀도의 개념을 무게에 적용시킨 것이다. 여기서 비(specific)는 단위라는 말로 숫자 "1"을 의미한다. 즉, 체적
"1" 단위당 무게 또는 단위 부피당 중량을 말한다. 또한 비중량은 밀도가 받는 중력에 의한 힘이라 할 수 있으므로 비중
량은 밀도 × 중력가속도로 나타낼 수 있다. 무게는 질량과 중력가속도의 곱이므로 마찬가지로 비중량은 밀도 × 중력가
속도가 된다. 4[℃] 물의 비중량은 물의 밀도 1,000 [㎏/㎥] × 중력가속도가 되므로 1,000 [㎏f/㎥]가 된다.

수은의 비중량은 수은의 비중은 13.6 으로 다음과 같이 나타낼 수 있다.
수은의 비중량 = 수은의 비중 × 물의 비중량

5. 비체적(specific volume)이란 무엇인가 ?
▣ 비체적(specific volume)은 단위 질량당 체적(부피)를 말한다. 수식은 비체적 = 부피 (V) / 질량 (m)이다. 밀도와
역수 관계에 있다. 유체역학이나 열역학에 자주 등장하는 단위이므로 숙지하는 것이 필요한다.
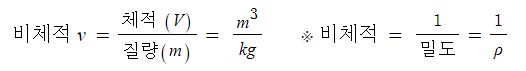
6. 비중이란 무엇인가 ?
▣ 비중(specific gravity)은 물의 밀도에 대한 물질의 밀도 비율을 말한다. 일반적으로 액체의 밀도는 표준대기압 즉 1기압
(1[atm]) 상태에서 4[℃]의 물(water)를 기준으로 물에 대한 대상 물체의 밀도의 비율을 말한다. 비중의 기호는 SG이고
비중은 밀도를 밀도로 나눈 것으로 단위가 없는 무차원수이다.

7. 압력, 방수압, 방사압, 토출압
▣ 압력, 방수압, 방사압, 토출압은 압력의 여러 표현방법이며 압력은 단위 면적당 작용하는 힘을 말한다.
수식으로 압력 = 힘 / 면적으로 표현한다. 기호로는 P를 쓰며 단위로는 N/㎡, kgf/㎡를 쓴다.

8. 수두, (전)양정, 높이 (H)
▣ 에너지 보존법칙과 베르누이 법칙에서 위치에너지를 말한다. 위치에서는 특정 위치가 갖는 일할 수 있는 능력 즉 에너지
를 말하며 위치에너지는 중력가속도와 높이의 곱으로 나타낸다. 그러나 표현의 편의상 소방유체에서는 중력가속도를
생략하고 높이만으로 위치에너지를 표현한다.
수두, 양정 = 중력가속도 × 높이 ⇒ 간략히 높이 [m]
9. 중력가속도
▣ 지구가 물체를 끌어 당기는 힘을 산정하기 위한 상수를 말한다. 기호는 g를 쓰고 단위는 가속도 이므로 m/sec2이고
값은 9.8 m/sec2 이다.
10. 체적, 부피 (v) : 단위 [㎥]
11. 질량 [㎏], 무게 [㎏f]
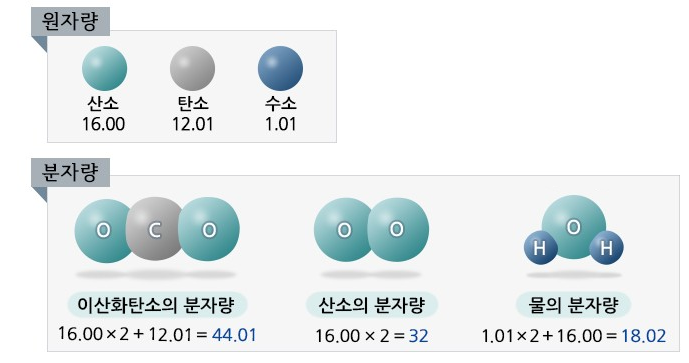
12. 분자량 (M) : CO2 : 44 , 할론 : 148.95
13. 온도 (T)
▣ 섭씨 : 물이 어는 점을 0[℃] 끓는 점을 100 [℃]로 하고 이들 간격을 백등분 한 것. 단위 : ℃
▣ 화씨 : 물의 어는 점을 32 [˚F], 끓는 점을 212 [˚F]로 하여 이들을 180 등분 한 것. 단위 : ˚ F
▣ 절대온도 [ ˚ K = 273 + ℃ ]
▣ 섭씨 온도와 화씨 온도의 변환

14. 기체 상수 (R) : 8.31385 [N·m/kmol ·K]
※ 압력단위가 atm일 경우 (0.082 atm · ㎡/kmol · K]

※ 고온, 저압의 기체는 일반적으로 이상기체방정식에 따른다.
기체 1몰은 0[℃], 1기압 (1atm)에서 22.414 [ℓ] 이므로 기체상수를 다음과 같이 구할 수 있다.
※ 표준온도와 압력 (standard temperature & pressure : STP) : 0[℃], 1[atm]
STP에서 실체 기체 ≒ 이상기체, 이 때 1[mol]의 기체 부피는 22.414 [ℓ]이다.

15. 유량, 체적유량, 방수량, 방사량, 토출량, 양수량 (Q)
▣ 유체역학에서는 물질의 상태를 어떤 좌표값으로 특정 지점을 통과하는 연속체의 개념으로 본다. 유체는 수많은 입자들
로 구성되어 있기 때문에 각각의 입자들을 분석대상으로 보는 것이 아니라 특정 지점을 통과하는 연속체의 개념으로
분석한다,
▣ 따라서 유량도 특정시점에서 관의 어느 부분을 통과하는 연속적인 양의 개념인 체적유량을 개념으로 정의한다.
이 때 특정시점에 특정지점을 통과한 유체의 부피로 흐르는 유량을 나타내는 것이 체적유량이며 이를 소방유체역학에
서는 유량, 체적유량, 방사량, 토출량, 양수량 등으로 부르며 기호로는 Q를 쓰고 단위로는 [㎥/sec], [ℓ/min], [단면적(A)
[㎡] × 속도 v [m/sec]]으로 나타내며 유체의 부피는 온도, 압력 등에 따라 변화하므로 부피 유량을 나타낼 때는 온도와
압력을 함께 표시한다.
16. 질량 유량 (M)
▣ 위에서 말한 체적 유량이 측정하기도 쉽고 사용하기도 간편하나 부피는 온도, 압력에 따라 변화하므로 이를 보완하기
위해 도입된 것이 질량 유량이다. 질량은 어디 있든, 어떠한 환경이든 똑같고 또한 질량은 보존되기 때문이다. 질량 유량
은 유체입자의 양을 측정하는 개념이다.
▣ 즉, 질량유량은 단위 시간당 흐르는 유체의 질량(㎏)을 측정하는 것이며 시간당 유체의 흐른 유체의 질량(㎏)을 의미한
다. 단위로는 [㎏/s]를 쓰며 kg을 g, ton으로 s를 min, hour으로 쓰기도 한다.
측정방법으로는 ‘질량 유량 = 밀도 × 단면적 × 평균 유속, 질량유량 = 밀도 × 부피(체적) 유량’ 으로 나타낸다.
⊙ 질량유량 = 밀도 × 단면적 × 평균 유속 [kg/s]
⊙ 질량유량 = 밀도 × 부피(체적) 유량 [kg/s]
17. 중량유량 (G)
▣ 중량유량은 단위 시간당 흘러간 유체의 중량을 말하며 이는 질량유량에 중력가속도를 곱해 산정한다. 즉, 질량유량을
지구 중력으로 환산한 값이다. 기호로는 G를 쓰고 단위는 [N/s], [㎏f/s]를 쓴다.
산정식은 ‘중량 유량 = 중력가속도 × 밀도 × 단면적 × 평균 유속, 중량유량 = 중력가속도 × 밀도 × 부피(체적) 유량’ 으로
나타낸다.
⊙ 중량유량 = 중력가속도 × 밀도 × 단면적 × 평균 유속 [N/s, kgf/s]
⊙ 중량유량 = 중력가속도 × 밀도 × 부피(체적) 유량 × 평균 유속 [N/s, kgf/s]
18. 단면적 (A)
▣ 유체는 대부분 원형관을 통해 공급되므로 단면적은 일반적으로 원의 면적이 된다.

19. 구경, 관경, 내경, 직경 (D) : [m, ㎜]
20. 유속, 속도 (v, u) : [m/s]
21. 각종 계수 (C) : 유량 계수 등
22. 동력 (P)
▣ 동력을 일률과 같다. 단위는 [J/s], [W] 를 쓴다.
⊙ 1[HS] = 0.746 [kW]
⊙ 1[PS] = 0.735 [kW]
23. 효율 [η]
▣ 효율은 입력 대비 출력을 말한다.

24. 전달계수 (K)
▣ 전달계수는 에너지 변환과정에서 손실을 감안하여 여유율을 두는 정도이다.
⊙ 전동기의 경우 통상 1.1 ~ 1.2 정도의 여유률을 둔다.
25. 전압, 정압 (P)
▣ 유체가 정지해 있을 때 또는 등속도 운동을 할 때의 압력을 정압이라고 한다.
⊙ 기호로는 P를 쓰고 단위로는 [㎜Aq, ㎜H2O] 등을 쓴다.
26. 마찰손실계수 (f)
▣ 유체의 입자간의 충돌 등 입자의 운동에 의한 손실율을 나타내는 계수를 말한다.
27. 길이 (L) : [m, ㎜]
28. 조도 (C) : 관 등의 거칠기 등을 말한다.
29. 회전수 (N) : [rpm, rps]
#밀도 #질량 #중량 #비중 #비중량 #비체적 #압력 #중력가속도 #체적 #기체상수
#체적유량 #질량유량 #중량유량 #마찰손실계수
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 소화설비 (0) | 2024.09.23 |
|---|---|
| 물질의 성질 (중력가속도, 질량, 밀도) (2) | 2024.09.23 |
| 소방시설의 종류 (소방시설법 시행령) (2) | 2024.09.13 |
| 창고시설의 화재안전성능기준 (2) | 2024.09.12 |
| 공동주택의 화재안정성능기준 및 화재안전기술기준 (6) | 2024.09.11 |