물체의 운동 상태를 변화시키려고 하는 외력에 저항하는 성질의 힘을 관성력(inertia force)이라 한다. 액체 상태인 물은 외력과 관성력에 평형하도록 운동한다. 물의 거동을 해석하기 위해서는 외력인 중력, 압력, 물의 밀도, 압축성, 점성 등의 물리적 성질에 관한 이해가 필요하다.
어떤 물질의 단위체적에 대한 질량의 비를 밀도(density)라 하며, 지구 중심에서 물체를 잡아 당기는 가속도를 중력가속도로 한다. 단위중량(unit weigth)은 단위 체적당의 중량으로 밀도와 중력가속도를 곱한 값이다. 질량과 단위중량과의 관계를 좀 더 살펴보기 위하여 먼저 중력가속도에 대해 좀 더 알아 보자. 뉴턴이 발견한 만유인력은 행성의 반경을 R, 질량을 M (행성의 질량), m (물체의 질량), 중력상수를 G(gravitational constant)라 하면 어떤 물체에 작용하는 중력은 GmM/R2 으로 나타낼 수 있다. 행성이 지구처럼 크다면( 반경 약 6,370km) 행성의 표면에서 어느 정도 떨어진 곳이라 할지라도 지구 반지름에 비해 아주 미소한 크기이므로 중력은 행성 표면과 거의 비슷하다고 할 수 있다.
지구에서 질량 m인 물체에 작용하는 중력(W)은 중력가속도를 g(9.8m/s2)라 하면 뉴턴의 제2법칙에 의하여 다음과 같이 표현된다.
W = mg 식 (1.1)
따라서 지구에서 중력에 의한 중력가속도는 다음과 같이 나타낼 수 있다.
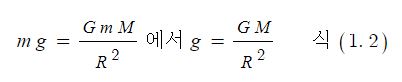
식 (1.1)에서 알 수 있듯이 중력가속도는 물체의 질량과 관계가 없다. 행성(지구)의 질량과 관계가 있다. 식 (1.1)와 식 (1.2)에서 나타낸 바와 같이 물체의 무게는 만유인력, 즉 중력으로 중력가속도가 지구 중심에서 얼마나 떨어져 있는냐 (장소)에 따라 다르기 때문에 같은 물체라도 무게는 장소에 따라 다르다. 지구는 일반적으로 적도의 반경이 크고 극지방의 반경이 작으므로 같은 물체의 중량은 적도 지역에서 보다는 극지방에서 약간 클 것이다.
물체의 체적을 V, 중량을 W, 중력 가속도를 g, 질량을 m 이라고 하면 밀도 와 단위 중량 는 다음과 같이 나타낼 수 있다.
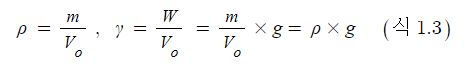
여기서, 중량의 차원은 [W] ≒ [F] ≒ [MLT−2] , 중력가속도의 차원은 [g] ≒ [LT−2], 부피
의 차원은 [Vo] ≒ [L3] 이다. 따라서 밀도와 단위중량의 차원은 MLT와 FLT에서 각각 다음과 같이 표현된다.
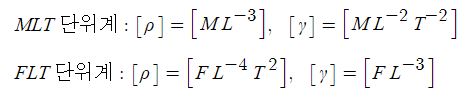
따라서 MLT와 FLT 차원에서 밀도의 단위는 각각 kg/m3과 kg/m2 ⋅ s2이고,
단위중량의 단위는 각각 kgf ⋅ s2/m4과 kgf/m3이다.
물의 밀도는 근소하지만 동일 기압이라 할지라도 수온에 따라서, 동일 온도라 하더라도 압력에 따라서 변화한다.
#밀도 #비중량 #가속도 #중력가속도 #만유인력 #뉴턴 #차원 #질량 #중량
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 옥내소화전설비 (수정) (14) | 2024.09.24 |
|---|---|
| 소화설비 (0) | 2024.09.23 |
| 단위 · 약칭 정리 (2) | 2024.09.19 |
| 소방시설의 종류 (소방시설법 시행령) (2) | 2024.09.13 |
| 창고시설의 화재안전성능기준 (2) | 2024.09.12 |