1. 역적 운동량 방정식
▣ 역적이란 말은 일정한 시간 동안 힘이 쌓인다는 뜻으로 힘의 적분을 의미한다.
배관내에 질량이 m인 물체가 dt 시간 만큼 움직인 경우에 배관내의 유속이
V1에서 V2로 변했다고 가정을 하고 이 때 유체에 작용하는 힘을 구해 보자.
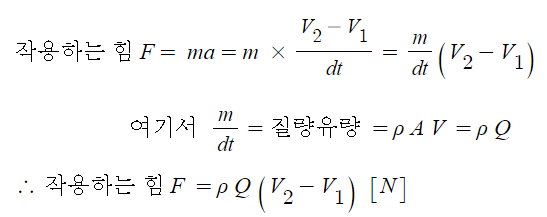
2. 고정 평판에 작용하는 힘
노즐에 의하여 고정 평판에 유체를 분사했을 때 고정 평판에 작용하는 힘을 구해 보자.
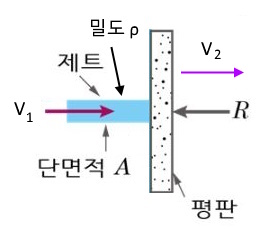
위 그림에서 유동하는 유체가 고정 평판에 미치는 힘은 평판이 V2의 속도로 이동한다면
평판에 부딪힌 유체도 V2의 속도로 이동하게 되므로 다음과 같이 나타낼 수 있다.
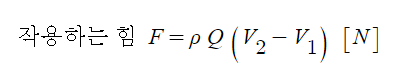
그런데 고정된 평판이라면 유체의 수평방향 유속 V2 = 0 되므로 다음과 같이 된다.

여기서 부호 (-)는 유체가 흐르는 방향과 반대방향으로 힘이 작용한다는 의미이다.
또한 체적 유량 Q = A · v 이므로 이를 위식에 대입하면
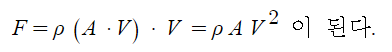
3. 경사면에 작용하는 힘
다음 그림과 같이 평면에 경사지게 노즐로 유체를 분사했을 때 작용하는 힘을 구해 보자.
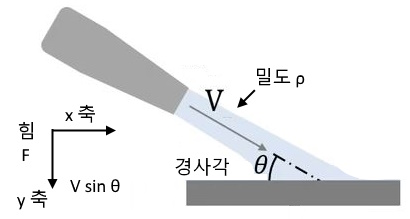
위 그림에서 유체가 평판에 부딪혀 정지하고 유체에는 점성도 없다고 가정하고 작용하는 힘을 수직축 즉 중력에 의한 힘만을 구해 보면 다음과 같다.
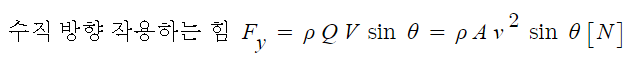
4. 곡면에 작용하는 힘
다음 그림과 같이 곡관 속에 흐르는 유체가 곡면에 작용하는 힘을 구해 보자.
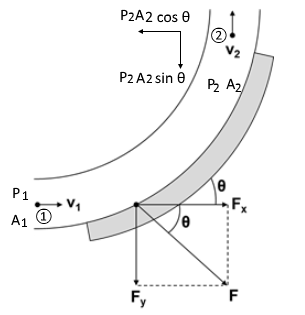
먼저, ①, ② 지점에서의 힘의 x축 성분, y축 성분과 속도의 x축 성분, y축 성분을 알아 보자.
먼저 속도 성분을 x축과 y축 성분으로 나누어 보면 다음과 같다.
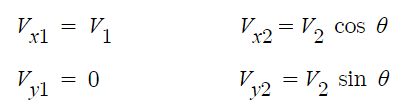
① 지점에서의 힘의 성분은 다음과 같다.

② 지점에서의 힘의 성분은 다음과 같다.
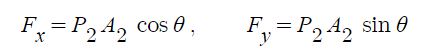
이제 곡면에 작용하는 힘의 x성분을 알아 보자. 운동량 방정식에서 힘이 작용한 만큼 운동량이 변화하므로 힘의 변화량은 운동량의 변화량과 같게 되어 다음의 식이 성립한다.
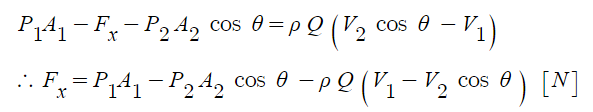
힘의 y성분을 구해 보면
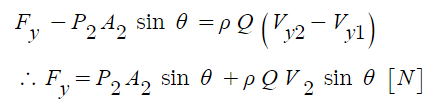
그런데 위에서 곡관의 면적이 같고 (A1 = A2), 유속이 ① 지점과 ② 지점에서 같다고 가정하면 힘의 x성분과 y성분은 다음과 같이 나타낼 수 있다.
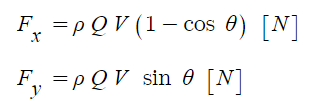
5. 베인 중심선이 받는 힘
베인이란 유체가 흐르고 있는 배관내에 수직으로 회전할 수 있도록 만들어진 날개를 말하며 일반적으로 평판을 휘어지게 만든 것을 말한다.
아래 그림과 같이 노즐에서 분사된 유체가 베인에 힘을 작용하여 베인을 회전하게 만들 때 작용하는 힘을 구하여 보자.
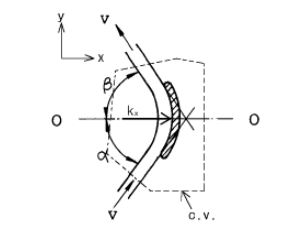
이 때 작용하는 x축과 y축에 작용하는 힘은 다음과 같다.
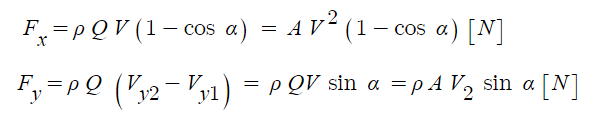
베인 중심선에 작용하는 힘은 다음과 같다.
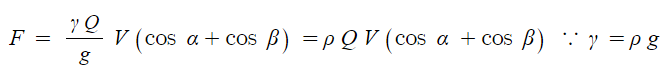
6. 분류 추진 (추진력)
아래 그림과 같이 유체를 분출시키면 그 반발력으로 물체가 앞으로 나가게 되는데
이를 추진력, 분류 추진이라고 한다.
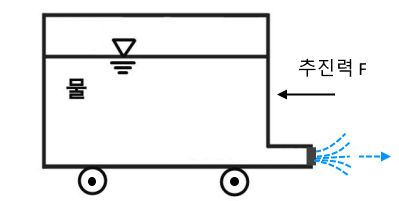
이 때 분류 추진으로 물체가 전진하게 되는 것은 분출되는 물체가 질량이 있고 유체의 속도가 변하는 가속도에 의하여 반발력, 즉 추진력이 생기게 되는데 이 때 작용하는 힘, 추진력은 다음과 같다.
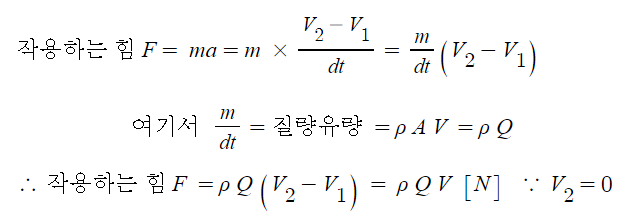
7. 노즐 플랜지에 작용하는 힘 (반발력)
어떤 배관에 유체의 속도를 높여 멀리 보내기 위해 구멍의 크기를 작게 하는 노즐을 설치하여 유체를 방사했을 때 유체가 방사하는 힘의 반발력으로 노즐의 플랜지에 힘이 작용하게 된다. 이 때 작용하는 힘을 구해 보자.
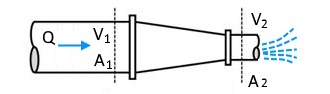
이 때 플랜지 볼트에 작용하는 힘은 다음과 같이 구할 수 있다.
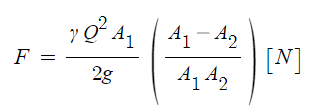
또 다른 산정식이 있는데 결과는 같다.
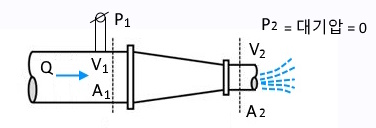
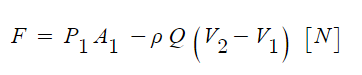
8. 운동에너지 수정계수
배관 내부의 유체의 속도가 항상 일정하면 좋겠는데 그렇지 않으므로 이를 보정하기 위해서는 운동에너지 수정 계수를 사용한다.

#운동량 #플랜지 #운동에너지 #질량유량 #체적유량 #경사면 #고정평판 #경사각 #날개각 #베인 #중심선 #추진력 #힘 #반발력 #수평 #수직
'소방설비기사 기계실기 이론' 카테고리의 다른 글
| 몰 (mol) 질량, 몰 부피, 입자수 사이의 관계 (2) | 2024.05.25 |
|---|---|
| 유효흡입수두 (NPSHav)와 필요 흡입 수두 (NPSHre) (2) | 2024.05.23 |
| [유체역학] 분류에 의해 작용하는 힘 (0) | 2024.05.20 |
| 운동량과 충격량 (Momentum & Impulse) (0) | 2024.05.19 |
| 베르누이 방정식과 토리첼리의 정리 (2) | 2024.05.14 |
