1. 유량
가. 연속방정식
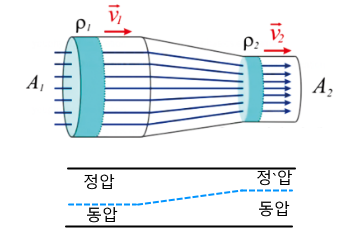
▣ 배관의 단면이 다른 관이 있다고 했을 때, 이 단면을 통해서 흐르는 유량은 항상 일정하다. 이는 에너지 보존의 법칙에
따른 것이다.
ρ1 · A1 · v1 = ρ2 · A2 · v2
⊙ 전압 = 정압(靜壓) + 동압 (動壓)
※ 관의 굵기에 관계없이 전압 (정압+동압)은 일정하다. 관이 굵으면 정압이 높이 동압이 낮으며 관이 가늘면 동압이 높고
정압이 낮다.
① 1차원 유동의 연속방정식
▣ 체적 유량 Q = A v : 체적유량 = 면적 × 유속
Q = A1 · v1 = A2 · v2
▣ 질량 유량 : m = ρ A v = ρ · A1· v1 = ρ · A2 · v2
▣ 중량 유량 : G = γ A v = γ · A1 · v1 = γ · A2 · v2
▣ 1차원 연속방정식의 미분
⊙ 질량 유량을 미분을 하면 연속방정식은 항상 일정하다는 것이므로 상수가 되는데 이를 미분하면 "0"이 된다.
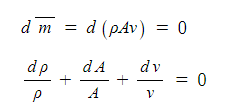
② 2차원 정상류 비압축성 유체의 연속방정식
⊙ x축과 y축에 대하여 편미분한 값을 합한 값이 "0"이 된다.
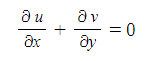
ex : x축 방향의 속도 성분을 u = x2 - y2, y방향의 속도성분을 v = -xy라고 한다면 연속방정식 성립여부
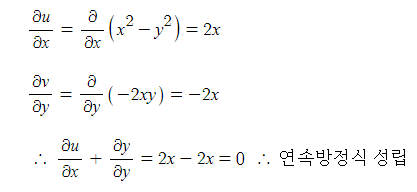
2. 유량 및 유량계수
▣ 유량계수는 어떤 특정관에서 유체의 흐름을 특정해 주는 지수를 말한다.
Q = A · v 에서 Q = C · A · v 로 표현한다. 여기서 C는 유량 계수이다.
▣ 유량계수는 유체의 수축유량계수와 속도 유량계수의 곱으로 나타낸다.
Cq = Co × Cv = A × Co × v ×Cv
가. 유량 측정 : 벤츄리 미터
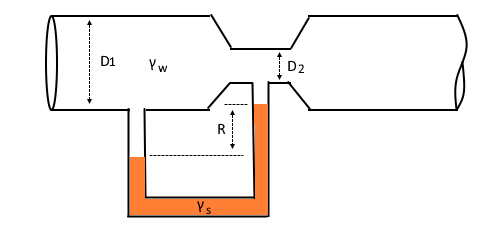
벤츄리 유량측정식은 다음과 같다.

나. 물탱크의 유량

▣ 수조내 증가하는 유량
⊙ 유입수량 - 토출유량
▣ 소화용수의 사용시간
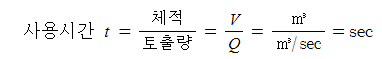
다. 노즐에서 방사량
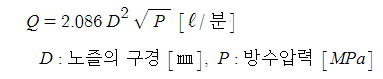
라. 소방차의 방수량
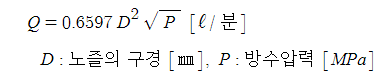
마. K-factor (유량계수)가 주어졌을 때

※ 수력반경과 수력 직경

※ P : 유체가 접하고 있는 관의 둘레 길이
A : 관의 단면적
ex : 위의 정사격형의 수력반경과 수력직경을 구하면
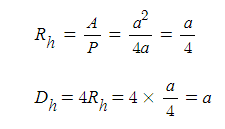
【 출제 예상 문제】
1. 다음 식에서 연속방정식이 아닌 것은 ?

2. 392 [N/sec]의 물이 지름 20 [㎝]의 관 속에 흐르고 있을 때 평균유속은 약 몇 [m/sec] 인가 ?

3. 유동단면이 30[㎝] × 40 [㎝] 사각적 수로를 통하여 비중 0.86, 점성계수 0.027인 기름이 2[m/sec]의 유속으로 흐른다.
이 때, 수력 직경에 기초한 레이놀즈의 수는 얼마인가 ?
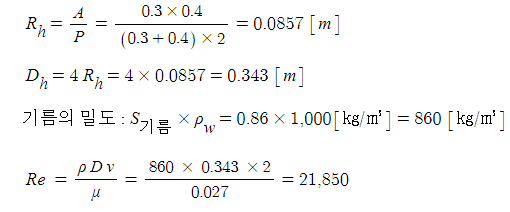
4. 직경 20 [㎝]의 소화용 호스에 물이 질량 유량 1,000[㎏/sec]로 흐른다. 이 때의 평균유속은 약 몇 [m/sec]인가 ?
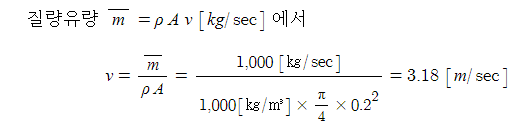
5. 연속방정식의 설명으로 가장 적합한 것은 ? ①
① 질량보존의 법칙을 만족한다.
② 뉴턴의 제2법칙을 만족시키는 방정식이다.
③ 단면적과 유량은 서로 반비례한다는 것을 구할 수 있다.
④ 연속방정식에 따르면 실제 유체의 경우 경계면에서 속도는 상대적으로 0 이어야 한다.
6. 그림과 같은 관을 흐르는 유체의 연속방정식을 맞게 기술한 것은 ?
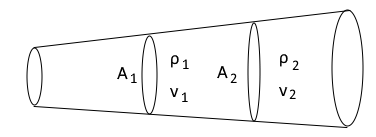
연속방정식은
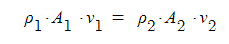
7. 내경 20 [㎝]의 매분 5.4 [㎥]의 물이 흐르고 있을 때 유속은 약 몇 [m/sec]인가 ?
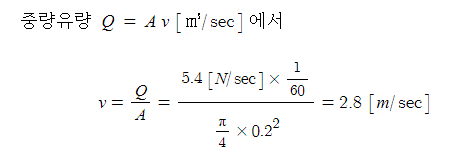
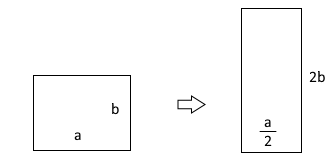
8. 직사각형 덕트에서 가로는 반으로 줄이고 세로는 2배로 늘리면 수력 직경은 몇 배가 되겠는가 ?
수력직경을 구해 보면
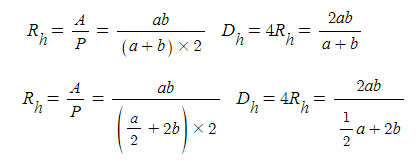
※ 변수가 하나가 아니라 2개 이므로 비교할 수가 없다.
9. 검사면을 통과하는 유동에 대하여 질량유동을 ρAv 로 구할 때 필요한 조건이 아닌 것은 ? ③
① 검사면은 움직이지 않는다. ② 밀도는 일정하다.
③ 검사면이 원형이다. ④ 유동은 검사면에 수직이다.
※ 관이 어떤 모양이든 단면적만 구하면 된다.
10. 수면의 면적이 10 [㎥] 인 저수조에 계속적으로 분당 1 [㎥]의 유량으로 채워지고 있다. 화재 초기에 수심은 2 [m] 였고
진화를 위해 분당 2 [㎥]의 물을 계속 사용한다면 이 저수조가 고갈될 때까지는 약 몇분이 걸리겠는가 ?
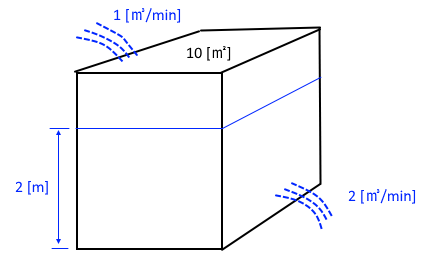
줄어 드는 양 : 1 [㎥/min] - 2 [㎥/min] = -1 [㎥/min]
고갈되는 시간 : T = 10 × 2 [㎥] ÷ 1[㎥/min] = 20 [min]
11. 안지름이 13 [㎜]인 옥내 소화전의 노즐에서 방출되는 물의 압력이 230 [kPa]이라면 10분 동안의 방출량은
약 몇 [㎥]인가 ?
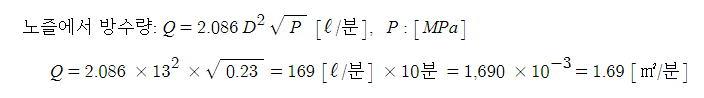
12. 소방차에 설치되어 있는 물탱크에 소화수원으로 2[㎥]이 채워진 상태로 화재 현장에 출동하여 구경이 21 [㎜]인 노즐을
사용하여 294.2 [kPa]의 방사압력으로 방사할 경우 물 탱크내 소화수원이 완전히 소모되는데 약 몇 분이
소요되겠는가 ?
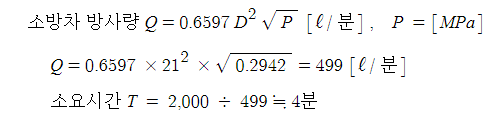
#유량측정 #벤츄리미터 #유량 #노즐 #방사량 #수력반경 #수력직경 #이중관 #연속방정식 #정상류 #압축성 #유량계수 #체적유량 #질량유량 #중량유량 #레이놀즈수
'소방설비기사 (기계) > 소방유체역학' 카테고리의 다른 글
| 펌프의 이상현상 (0) | 2023.09.06 |
|---|---|
| 배관의 주손실과 부차적 손실 (0) | 2023.09.05 |
| 유체의 유동과 레이놀즈 수 (0) | 2023.09.02 |
| 경사평면 및 곡면에 작용하는 힘 (0) | 2023.09.02 |
| 모멘트 (Moment) 란 ? (0) | 2023.09.01 |
