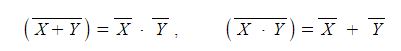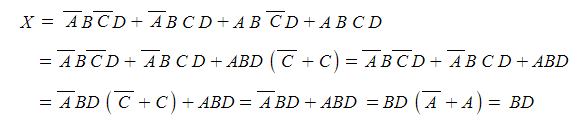아낌없이 주는 나무

1. 불(Boolean)대수 정리

​

▣ 논리의 구성과 식을 간단히 하기 위하여 불(Boolean) 대수, 드 · 모르간(De Morgan) 의 정리 등을 이용한다.

​

가. 분배법칙

   A + ( B · C) = (A+B) · (A+C)

   A · (B + C) = (A · B) + (A · C)

  ※ 논리연산에서는 논리합(+)도 분배법칙이 성립한다.

​

나. 2진수의 특성상 "0", "1" 및 논리변수 A, B에 대하여 다음식이 성립한다.

     논리합은 합집합, 논리곱은 교집합으로 생각한다. "1"은 전체집합의 의미이다.

​

① A + 0 = A

     A · 1 = A (A집합과 전체 집합과의 교집합은 A이다)

​

② A + A = A (자신과 자신의 합집합은 자신이다)

     A · A = A (자신과 자신의 교집합은 자신이다)

​

③ A + 1 = 1 (자신과 전체 집합 "1"과 합집합은 전체 집합 "1"이다.

​

④ A · 0 = 0 ("0" 집합과 자신과의 교집합은 "0"이다.

​

⑤ 0 + 0 = 0 ("0" 집합과 "0" 집합의 합집합도 "0"이다)

     0 · 1 = 0 ("0" 집합과 "1" 전체 집합의 교집합은 "0"이다)

​

⑥ 0 + 1 = 1 ("0"집합과 전체집합 "1"과 합집합은 전체집합 "1"이다)

     1 · 1 = 1 (전체 집합 "1"과 전체집합 "1"과 교집합은 전체집합"1"이다)

​

⑦ 0' = 1 ("0"의 반대는 "1"이다)

     1' = 0 ("1"의 반대는 "0"이다)

​

【불(Boolean) 대수 기본 정리】

다. De Morgan의 정리

2. 논리회로

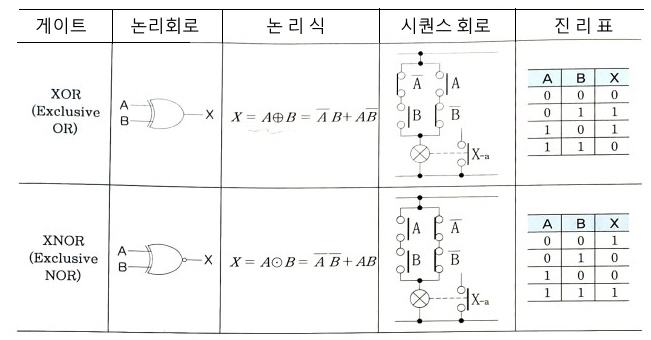
 ▣ 논리회로를 게이트, 논리식, 시퀀스회로 및 진리표와 비교하며 알아 보자

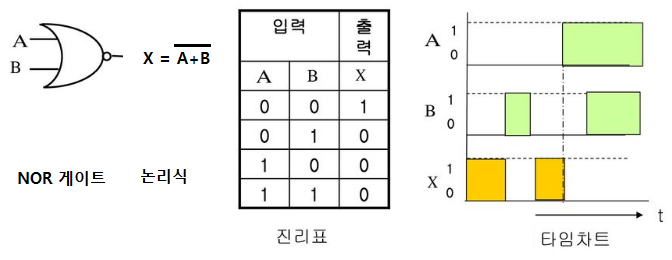
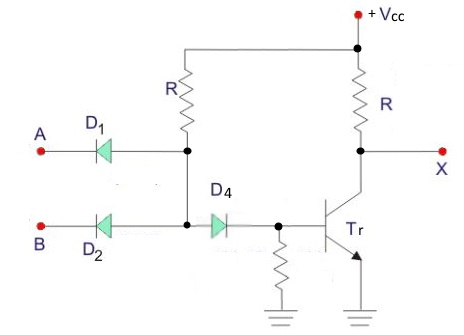
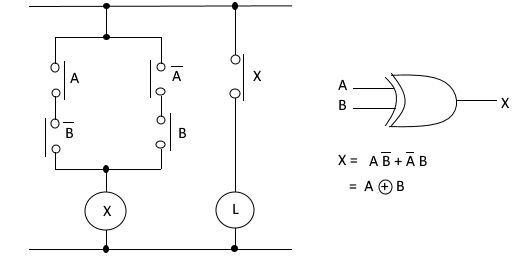
   ⊙ 우선 기본적인 논리회로에는 AND, OR, NOT, NAND, NOR, XOR, XNOR가 있다.

[이어서]

[참고] 논리회로의 치환 : 드 모르간의 정리

  ▣ 드모르간의 정리는 NOT을 이용하여 논리식을 단순화한다.

【 출제 예상 문제】

​

1. 다음의 표와 같이 두 입력 A와 B가 주어졌을 때 주어진 논리소자의 명칭과 출력에 대한 진리표를 완성하시오.

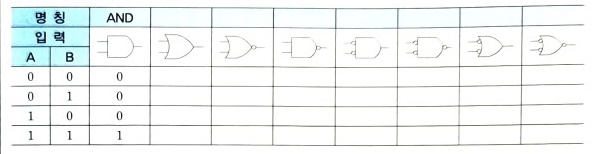
[답안작성]

2. 그림과 같은 논리회로를 이용하여 다음 각 물음에 답하시오.

  가. 3개의 입력단자 A, B, C에 각각 1의 입력이 들어 간다면 출력단자 X, Y에는 어떤 출력이 나오겠는가 ?

  나. X와 Y에 대한 논리식을 작성하시오.​

3. 감지기 회로의 배선방식으로 교차회로방식을 사용할 경우 다음 각 물음에 답하시오.

  가. 불대수의 정리를 이용하여 간단한 논리식을 쓰시오. X = A · B

  나. 무접점 회로로 나타내시오.

  다. 진리표를 완성하시오.

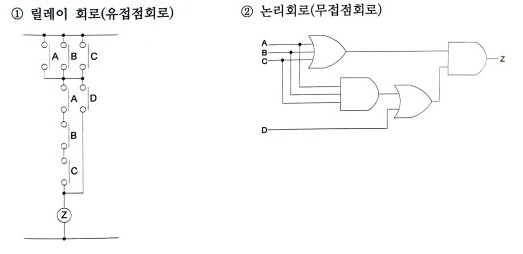
4. 논리식 Z = (A+B+C) · ( A · B · C + D)를 릴레이 회로 (유접점 회로)와 논리회로 (무접점 회로)로 바꾸어 그리시오.

5. 아래 그림과 같은 논리회로를 보고 다음 각 물음에 답하시오.

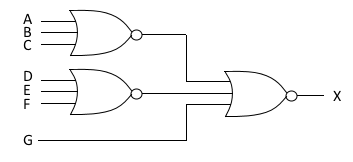
  가. 논리식으로 표현하시오.​

  나. AND, OR, NOT 회로를 이용하여 등가회로를 그리시오.

  다. 유접점(릴레이) 회로로 그리시오.

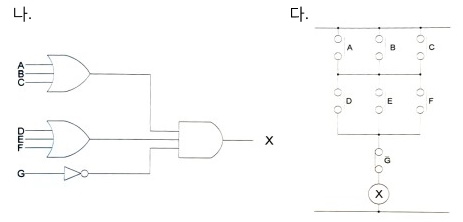
6. 아래 그림과 같은 스위칭 회로를 접점수를 최소화하여 논리식과 스위칭 회로를 도시하시오.

  ① 논리식​

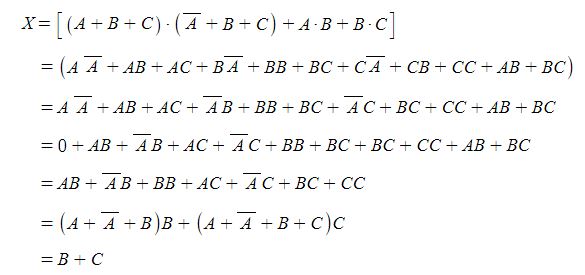
  ② 스위칭 회로

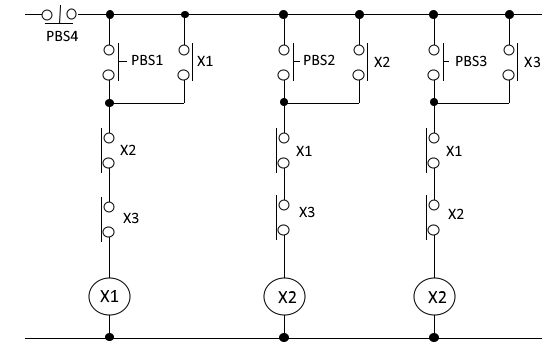
7. 아래 그림과 같은 유접점 시퀀스 회로에 대해 다음 각 물음에 답하시오.

  가. 그림의 시퀀스도를 가장 간략화한 논리식으로 표현하시오. (단, 최초의 논리식을 쓰고 이것을 간략화하는 과정을

         기술하시오.​

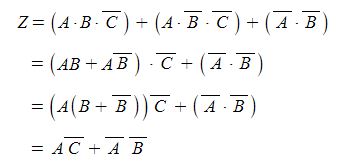
  나. 가.에서 가장 간략화한 논리식을 무접점 논리회로로 그리시오.

8. 다음 주어진 논리식을 릴레이 회로(유접점회로) 및 논리회로(무접점회로)로 바꾸어 그리시오.

  가. Z = A · B + A · B

  나. Z = (A + B) · (A + B)​

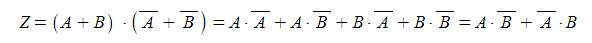
[회로도]

9. 논리식 X = A(B+C)이고 다음의 표와 같이 입력 A,B,C가 주어질 때 진리표를 완성 하시오.

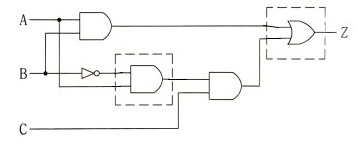
10. 논리식 Z = AB + ABC 일 때 다음 논리회로의 미완성 부분을 완성하시오.

  [답안작성]

#부울대수 #불대수 #Boolean #드모르간 #드모르간정리 #DeMorgan #논리회로

#논리합 #논리곱 #시퀀스 #시퀀스회로 #진리표 #교차회로 #무접점회로 #유접점회로

#릴레이회로 #AND #OR #NAND #NOR #NOT #스위칭회로 #배선방식

1. 논리회로

         #디지털    회로         0                   1

                                         Off               On

                                         Low            High

​

가. AND 회로

  ▣ 입력 신호 A, B가 있을 때 출력이 나오는 회로이며 스위치의 직렬회로이다.

    ① 논리기호 및 논리식

   ② #타임차트 

    ② 회로도 및 타임차트

라. NAND 회로

  ▣ #AND 회로와 NOT회로의 합으로 AND회로를 부정하는 판단기능을 갖는 만능회로다.

마. NOR회로

  ▣ OR회로와 NOT회로의 합으로서 OR회로를 부정하는 판단기능을 갖는 회로이다.

  ② 시퀀스 회로도

사. 논리식 요약

아. 논리회로 변환

  ① NABD 게이트의 3가지 연산 변환

  ② NOR #게이트 의 3가지 연산 #변환

2. 부울대수

  ▣ 임의의 회로에서 일련의 기능을 수행하기 위한 가장 최적의 방법을 결정하기 위하여

       이를 수식적으로 표현하는 방법을 #부울대수 (Boolean algebra)라 한다.

가. 부울대수 의 정리

    (정리1) X + 0 = X X · 0 = 0

    (정리2) X + 1 = 1 X · 1 = X

    (정리3) X + X = X X · X = X

    (정리4) X + X = 1 X · X = 0

    (정리5) X + Y = Y+ X X · Y = Y · X ( #교환법칙 )

    (정리6) X + (Y + Z) =(X + Y) + Z, X(YZ) = (XY)Z : #결합법칙

    (정리7) X(Y+Z) =XY+XZ, X+YZ = (X+Y) (X+Z) : 배분법칙

                 (X+Y) (Z+W)=XZ+XW+YZ+YW : #배분법칙

    (정리8) X+XY = X, X+XY = X + Y : #흡수법칙

나. #드모르간의 정리​

【 출제 예상 문제】

​

1. 그림과 같은 무접점회로는 어떤 논리회로인가 ? ③

         ① NOR              ② OR              ③ NAND                 ④ AND

        [해설] NAND 게이트 회로도

​

2. 그림과 같은 계전기 접점회로를 논리식으로 나타내면 ? ①

[보기]​

    [해설] #시퀀스 회로와 논릭식 : 직렬연결은 #논리곱 , 병렬연결은 #논리합

​

3. 다음과 같은 #다이오드 논리회로의 명칭은 ? ②

    ① NOR회로            ② AND 회로                 ③ #OR회로              ④ #NAND 회로

​

4. 논리식 X · (X+Y)를 간략화하면 ? ①

    ① X               ② Y                 ③ X+Y                  ④ X · Y

  [해설] 부울대수의 흡수법칙

        ⊙ X · (X+Y) = XX + XY = X + XY = X (1+Y) = X​

[문제6]​

7. 그림과 같은 논리회로의 출력 X는 ? ④

[보기]​

8. 그림과 같은 논리회로의 출력 L을 간략화한 것은 ? ②

[보기]​

9. 그림과 같은 논리회로는 ? ②

    ① OR회로              ② AND 회로               ③ NOT 회로              ④ NOR 회로

​

10. 입력신호 A,B가 동시에 "0"이거나 "1"일 때만 출력신호 X가 "1"이 되는 게이트의 명칭은 ? ①

    ① EXCLUSIVE NOR       ② EXCLUSIVE OR      ③ NAND          ④ AND

[해설] 진리표를 작성하여 해당 논리회로를 추정해 본다.

[논리식]

​

1. 시퀀스 제어

 가. AND 회로

 (1) 유접점 회로, 무접점 논리회로, 논리식

 (2) 진리표

나. OR 회로

 (1) 유접점 회로, 논리회로 및 논리식

 (2) 진리표

다. 배타적 논리합 (E-OR, X-OR, EX-OR)

 (1) 유접점회로, 논리회로 및 논리식

 (2) 진리표

라. 부울대수와 드모르간 정리

  (1) 부울대수 (반드시 외울 것)

  (2) 드모르간 정리

마. 카르노맵

  ▣ 3변수 이상 논리식을 간소화하는데 매우 편리한 간소화 기법이다.

  ▣ 카르노맵에서는 3변수를 카르노맵에 해당되는 칸에 표시하고 해당 칸의 묶음 내에서

      가로, 세로 방향으로 변하지 않은 변수의 곱이 간소화된 논리식이다.

(1) 3변수 논리식 간소화

  ▣ 카르노맵에 의해 간소화

   ▣ 카르노맵에 의해 간소화

(2) 타임차트

사. 시한회로 (On Delay Timer : TON)

  (1) 논리회로

(2) 타임차트

아. 전동기 정역 운전회로

  (1) 주회로

(2) 보조회로

[동작설명]

  ① BS1 (ON) ⇒ MC1 (여자), RL1 (점등), GL (소등)

  ② BS2 (ON) ⇒ MC2 (여자), RL2 (점등), GL (소등)

  ③ 과부하 ⇒ Thr 동작 ⇒ OL (점등)

​

【예상 적중 문제】

​

1. 그림과 같은 무접점 논리회로에 대응하는 유접점 릴레이회로(시퀀스) 회로를 그리고,

     논리식으로 표현하시오.

     [답안작성]

 2. 주어진 논리회로의 출력을 입력변수로 나타내고, 이 식을 AND, OR, NOT 소자만의

    논리회로로 변환하여 논리식과 논리회로를 그리시오.

【문제풀이】

먼저 논리식으로 표현을 한 후에 논리식을 단순화한 다음에 논리회로를 재구성한다.

   ▣ 위 논리식을 논리회로 표현하면 다음과 같다.

(2) 유접점 회로

   (3) P1~P3 의 출력식

4. 다음 논리식에 대한 물음에 답하시오. (단, A,B,C는 입력, X는 출력이다)

  (1) 논리식을 로직 시퀀스로 나타내시오.

  (2) 물음 (1)항에서 로직 시퀀스로 표현된 것을 2 입력 NAND gate를 최소로 사용하여

       동일한 출력이 나오도록 회로를 변환하시오.

  (3) 물음 (1)항에서 로직 시컨스로 표현된 것을 2 입력 NOR gate를 최소로 사용하여

       동일한 출력이 나오도록 회로를 변환하시오.

 [답안작성]

  (1) 논리식을 로직 시퀀스로 나타내시오.

(2) 물음 (1)항에서 로직 시퀀스로 표현된 것을 2 입력 NAND gate를 최소로 사용하여

     동일한 출력이 나오도록 회로를 변환하시오.

  ※ 식을 먼저 NOR gate로 변환하자.

(3) 물음 (1)항에서 로직 시컨스로 표현된 것을 2 입력 NOR gate를 최소로 사용하여

     동일한 출력이 나오도록 회로를 변환하시오.

   ※ 식을 먼저 NAND gate로 변환하자.

5. 다음 논리식을 간단히 하시오.

  (1) Z = (A+B+C) · A = AA+AB+AC = A+AB+AC = A (1+B+C)

           = A

   (2) 타임차트​