아낌없이 주는 나무

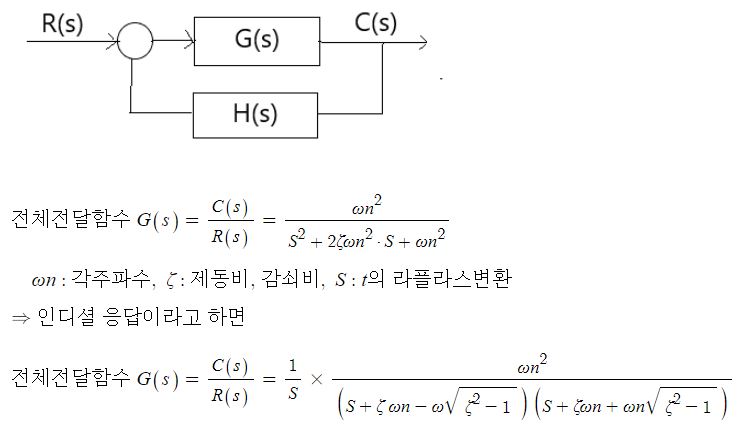
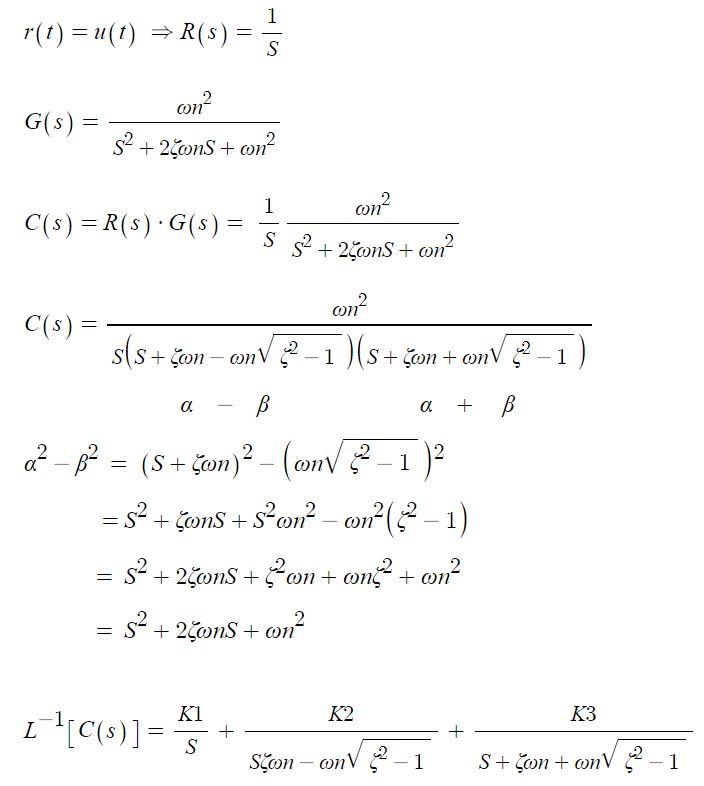  ◎ 상태공간법 : 현재의 회로를 바탕으로 미래를 예측하는 것

  ◎ 상태방정식 : 계통방정식이 n차 미분방정식일 때, 이것을 n개의 1차 미분방정식으로

                            바꾸어서 행렬을 이용하여 표현한 것

  ※ 미분방정식 ⇒ 3개의 1차 미분방정식 (행렬) ⇒ 상태천이방정식(상태천이행렬)

     (3차방정식)                        (상태방정식)

                       * 답 찾는 방법 정도만 다룸

​

1. 상태 방정식 

    ※ 시스템행렬과 제어행렬로 나타 내는데 시스템 행렬이 더 중요함

​◎ 상태천이방정식 : 입력 r(t)="0"이고 초기 조건만 주어졌을 때, (초기시간 이후에는

                                 어떤 현상이 나타나는가?) 초기시간 이후에 나타나는 계통의

                                 시간적 변화상태를 나타내는 행렬식

  ※ 상태천이 방정식 안에 상태천이 행렬이 있음

       상태방정식의 일반식

   ※  상태천이행렬의 성질

3. Z변환

 ※ "L" 라플라스변환 : 연속인 선형적 시스템, 규칙적 시스템

    "Z" 변환 : 불연속인 비선형 시스템, 불규칙 이산 시스템

​

① Z변환과 라플라스 변환

③ Z변화의 중요정리​

4. 가제어, 가관측

   : 제어의 기능과 불가능, 관측의 가능과 불가능을 판별한다.

※ 라플라스 전환

  o 시간함수(t)는 해석은 쉽지만 계산이 어렵기 때문에 라플라스 변환하여 계산한 후

     다시 역 라플라스 변환을 하여 전체를 해석하게 된다.

라플라스함수는 계산은 쉽지만 해석이 불가능

반대로 시간함수는 해석은 쉽지만 계산이 어려움​​

가. 단위계단 응답(인디셜 응답)

​

  ⊙ 입력으로 단위 계단 입력 (u(t)=1/s)을 넣었을 때의 출력

     ⇒ R (t) = u (t) = 1 / s

    ※ 단위 계단 응답(인디셜 응답)이란 ? : 입력으로 [u(t) → 1/s]을 입력시 출력을 말함

라. 2차 지연계(R-L-C 과도응답)에서 인디셜 응답​​

2. 제동비, 감쇠비 ζ

3. 특성방정식 - 2차 지연

​ ※ 특성방정식 : 전체 전달함수의 분모가 "0"이 되는 방정식​

① 특성방정식을 이용한 회로의 안정·불안정 해석

<1차 지연 제어계의 과도 응답>

⇒ 인디셜 응답

<특성방정식의 근의 위치별 과도 응답>​

(4) 영점과 극점 (제6강)

① 영점 (Zero)은 분자가 "0"이고 단락상태

   ⊙ Z(s) 임피던스는 분자가 "0"이 되는 "S"를 영점이라 하며 회로의 단락상태를 말한다

   ⊙ M(s)=0 ⇒ 분자 = 0 좌표상 표시 O

​

② 극점(Pole)은 분모가 "0"이 되는 개방상태

   ⊙ Z(s) 임피던스는 분모가 "0"이 되는 "S"를 극점이라 하며 회로의 개방상태를 말한다.

   ⊙ M(s) = ∞ ⇒ 분모 = 0 좌표상 표시 X

​

5. 과도 응답의 시간 특성 - 2차 지연요소의 인디셜 응답

  ※ 3장 전체중 시험에 제일 잘 나옴

⊙ 오버슈트 : 응답중에 발생하는 입력과 출력 사이의 최대 편차량으로서 제어계의 안정도의 척도가 된다.

⊙ 지연시간(Delay) : 시작부터 목표값의 50%에 이르는 데 걸리는 시간

⊙ 상승시간(Rising) : 10%에서 90%에 도달하는데 걸리는 시간

⊙ 세팅(정정)시간 : 정상값의 ±5%에 들어 오기까지 걸리는 시간

​