1. 안정도
⊙ 특성방정식의 근으로 안정과 불안정을 파악한다.
◎ 안정도 : 안정도란 시스템이 불안정하면 과도응답과 정상상태의 오차들은 논의할
가치가 없게 되므로 불안정한 시스템은 특별한 과도응답이나 정상상태의
오차의 요구사항으로 설계될 수 없으므로 모든 제어회로는 반드시 안정되어야 한다.

⇒ 특성방정식이 2차식까지는 계산에 의해 근을 구할 수 있으나
3차식 이상일 경우에는 특성방정식의 근을 구하기 힘들다.
따라서...
① 절대 안정도 : 루스, 후르비쯔 : O, X 판별
② 상대 안정도 : 나이퀴스트 : 안정도의 정도까지 판별
③ 보드 선도
이 3가지 방법으로 안정도를 파악한다.
※ 제에계의 안정조건
⊙ 특성방정식 (1+G(s) · H(s))의 근이 모두 좌반평면에 있을 것
① 절대 안정도 : 루스 판별법
⇒ 안정 여부만 판별 가능 : O, X 판별

1. 모든 차수의 계수가 존재할 것
2. 모든 차수의 부호가 같을 것 (0차는 예외적으로 봄)
3. 루스표 1열의 부호가 같을 것
(루스표 1열의 부호 변화 수 만큼 근이 우반평면에 존재)

※ 루스표 만드는 방법

※ 부호가 바뀐 횟수 만큼 우반 평면에 근의 갯수가 존재한다.

| S4 | 1 | 3 | 5 |
| S3 | 2 | 1 | 0 |
| S2 | 2×3−1×12= 2.5 | 2×5−1×02= 5 | 2×0−1×02= 0 |
| S1 | 2.5×1−2×52.5= −3 | 2.5×0−2×02.5=0 | 2.5×0−2×02.5= 0 |
| S0 | −3×5−2.5×0−3= 5 | −3×0−2.5×0−3= 0 | −3×0−2.5×0−3= 0 |

② 상대안정도 : 나이퀴스트 안정도
⊙ 특성 방정식의 근들의 영점이 복소평면 우반부에 존재하는가를 벡터궤적을 통해 판별하는 방식
⊙ 특 징
◎ 절대 안정도(안정/불안정) 판단 가능
◎ 안정도를 개선할 수 있는 방법 제시
◎ 스스템의 주파수 영역 응답에 대한 정보 제공
※ 안정도 판별법
⇒ 개루프전달함수(G(jω) · H(jω))를 0 ~ ∞ 로 변화시킬 때
벡터 궤적이 (실부부 -1, 허수부 j0)인 점을
왼쪽으로 보면서 수렴하면 안정
오른쪽으로 보면서 수렴하면 불안정으로 판별

※ 위상의 여유와 이득의 여유
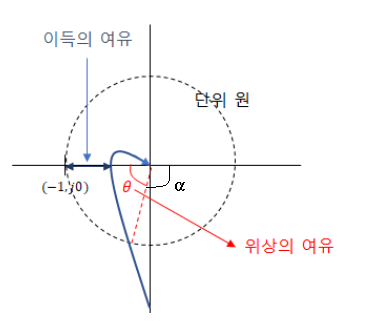
◎ 이득여유는 벡터궤적이 음의 실수축과 만나는 점과 판별점(-1, j0) 과 간격(차이)
◎ 이득 주파수 : 이득곡선과 단위 원과 만나는 점의 주파수
◎ 위상여유 Θ = 180˚ - α
- 단위 원과 만나는 점과 실수축과의 각도
◎ 위상의 여유와 이득의 여유가 크면 클 수록 안정하다는 것
※ 이득의 여유 구하는 방법
: G(s) · H(s)의 허수부가 0(jω=0)인 순간의 여유

예제1)
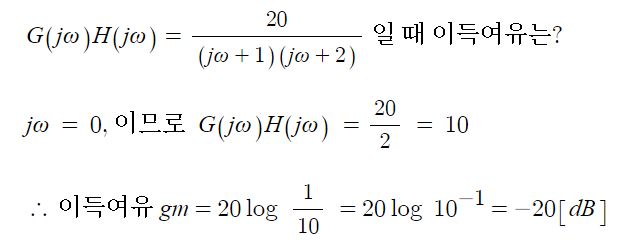
예제2)

③ 보드 선도에 의한 안정도 판별법
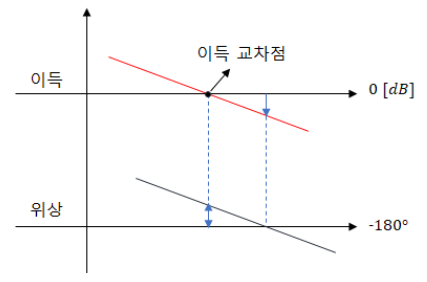
◎ 이득 교차점에서 위상이 -180˚ 보다 크고,
위상 곡선과 -180˚선 교차점에서 이득이 음수이면 "안정"
※ 안정도 문제

문제 6) S4+2S3+S2+4S+2=0 일 때 안정도는 ?

계수의 부호가 2번 바뀌었으므로 불안정, 우반평면에 근 2개
※ 차수에 "0"이 나오면 임계안정


문제10) 다음 전달함수일 때 안정을 위한 K의 조건은?
G(s) = 2K / S(S+1)(S+2)
풀이 : 1+G(s) · H(s) ⇒ H(s)=1, 단위 되먹임 함수
특성방정식 = 개루프 전달함수의 분모 + 분자 = 0
S(S+1)(S+2)+2K=0
S(S2+3S+2)=0, S3+3S2+2S+2K=0
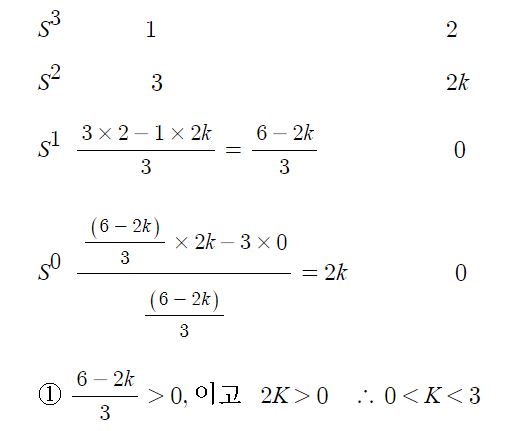

'전기인이 되는 길 > 제어공학' 카테고리의 다른 글
| 근궤적 (0) | 2023.01.10 |
|---|---|
| [연습문제] 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
| 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
| 자동제어계의 시간영역 해석 : 안정상태 (0) | 2023.01.10 |
| 자동제어계의 시간영역 해석 : 과도상태 (0) | 2023.01.10 |
비버리님의
글이 좋았다면 응원을 보내주세요!