반응형
1. 근궤적
S^2+3S+K = 0 이라고 할 때
상수 K 값이 변함에 따라 근이 변하게 되는데
근이 변함에 따라 안정 · 불안정을 판별할 수 있다.
⊙ 근 : 특성방정식의 근 - 안정과 불안정을 판별해 줌
⊙ S평면 상에서 개루프 전달함수(G(s)·H(s))의 이득상수 K를 "0"에서 ∞까지
변화시킬 때 근이 그리는 궤적
⇒ 근궤적을 통해서 안정, 불안정을 판별할 수 있다.
ex) 이득상수 K의 변화에 따라 계의 특성방정식의 특성근이 어떻게 변화하는가?

[근궤적 및 안정도]
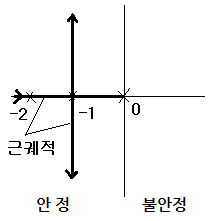
① k = 0, s = -2 or 0
② 0 < k < 1, s = 서로 다른 음의 실근
③ k = 1, s = -1 (중근)
④ k > 1, s = 음의 공액 복소수
⑤ k < 0, s = 양의 실수, 음의 실근, 불안정 가능
2. 근궤적 작성
① 근궤적의 출발 : 극점
② 근궤적의 도착 : 영점
③ 근궤적의 갯수 = 극점과 영점 중 많은 것의 갯수, 특성방정식의 최고 차수

④ 근궤적의 대칭 : 실수축 대칭

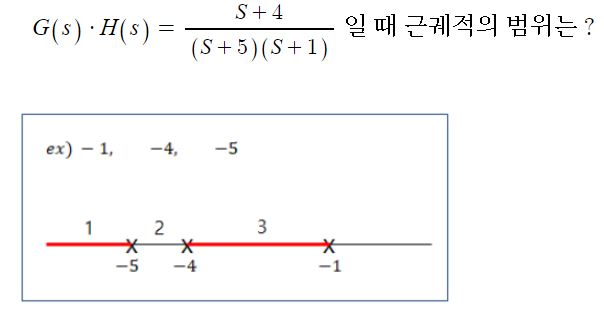
⑤ 실수축 상의 근궤적의 범위 :
⊙ 극점과 영점의 총 개수가 홀수 구간에만 존재 ( - ∞ 에서 부터 시작)
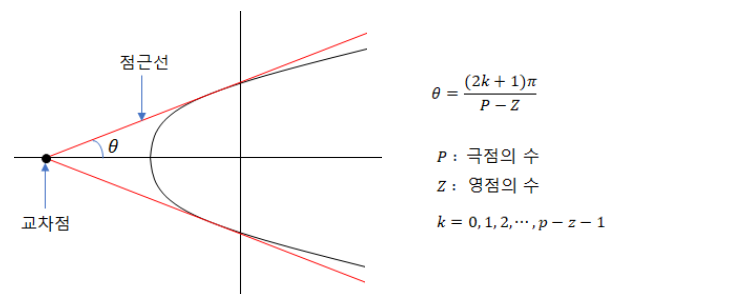
⑥ 근궤적 점근선의 각도
⊙ 1각도 실수축과의 내각
⊙ 2각도 실수축과의 외각
⊙ 3각도 180˚

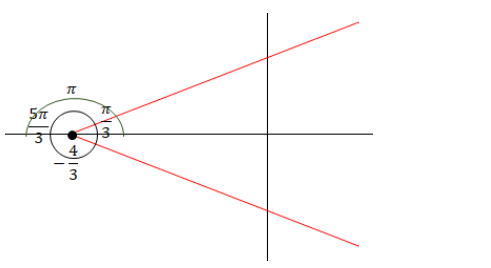
⑦ 점근선의 교차점

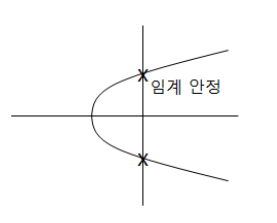
⑧ 허수축과의 교차점 ⇒ 임계 안정 (루스표로 판별) 조건으로 계산
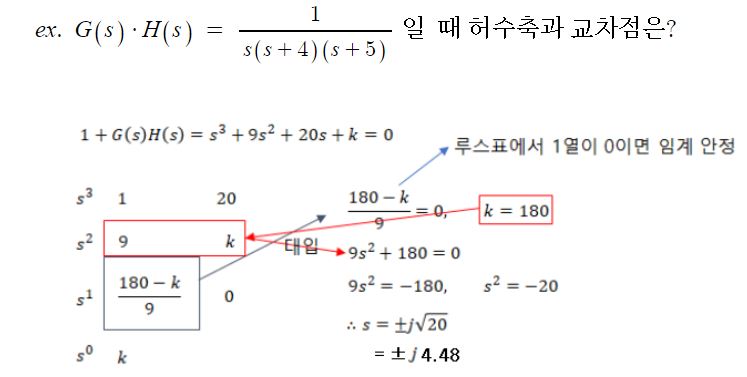
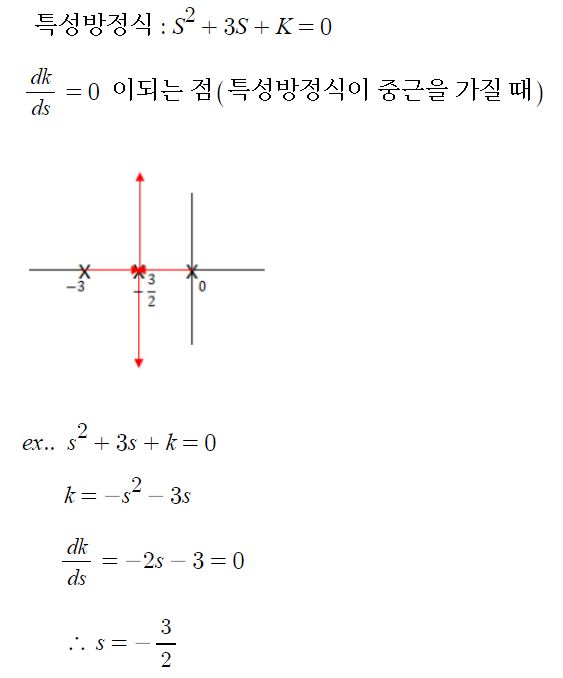
⑨ 이탈점, 분지점 : 특성방정식의 중근이 되는 경우
⊙ 근궤적이 나뉘어 지는 점



반응형
'전기인이 되는 길 > 제어공학' 카테고리의 다른 글
| 시퀀스 제어 (0) | 2023.01.10 |
|---|---|
| 상태공간법 (0) | 2023.01.10 |
| [연습문제] 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
| 제어계의 안정도 (2) | 2023.01.10 |
| 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
