⊙ 주파수 영역해석 : 입력 주파수가 0~ ∞ 로 변화할 때 출력의 크기나 위상변화 즉 벡터궤적이나 보드 선도를 보는 것
⊙ 주파수 응답 : 입력 주파수 변화에 대한 입력과 출력의 진폭비, 위상차가 어떻게 변화하는지 특성을 나타내는 것
⊙ 진폭비 : 출력크기 / 입력크기
⊙ 위상차 : 입력과 출력의 위상차
※ 시간영역 해석은 시간(t)를 라플라스 변환(s)하여 계산하여 역라플라스 변화하여 해석
주파수 영역해석은 시간(t)를 라플라스변환(s) 후 주파수변환(jω)하여 해석
f ⇔ ω = 2πf
주파수 영역 해석은 ω가 0 ~ ∞ 로 변할 때 영역해석
시간영역해석은 t가 0 ~ ∞로 변할 때 영역 해석
주파수 영역방법에는 벡터 궤적, 보드 선도가 있다.

1. 주파수 전달함수

2. 주파수 전달함수가 주어졌을 때 이득과 위상을 구하는 방법

위상계산시 전달함수가 분모에 있을 때 위상각은 앞에 "(-)"가 붙는다.
jb 형태시 각도는 j=90˚, -1=180˚, -j = 270˚
3. 벡터 궤적
⊙ 벡터궤적 : 주파수 전달함수 G(jω)를 복소평면상에 벡터로 나타낸 크기로서
G(jω)와 각도(Θ)에서 각주파수 G(jω)를 0 ~ ∞ 까지 변화시킬 때 그려진 궤적
G(jω) 에서 ω 가 0 ~ ∞로 변할 때
◎ 비례요소 : k ⇒ k
◎ 비분요소 : k · s ⇒ k · jω
◎ 적분요소 : k / s ⇒ k / jω
◎ 1차 지연 요소
◎ 2차 지연 요소
◎ 부동작 등
① 비례요소
G(jω) = K

② 미분요소
G(s) = k · s ⇒ G(jω) = k · jω

③ 적분요소
G(s) = k / s ⇒ G(s) = k / jω
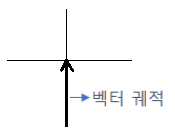
④ 비례미분요소
G(s) = 1+Ts ⇒ G(s) = 1+jωT
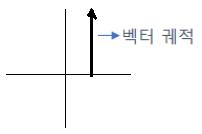
⑤ 1차 지연


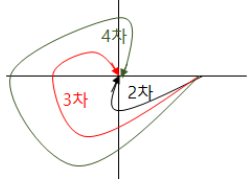
⑥ 2차 지연 (3차 지연, 4차 지연)
⑦ 부동작(K−τs)
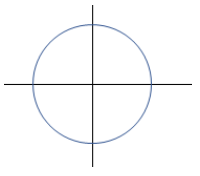
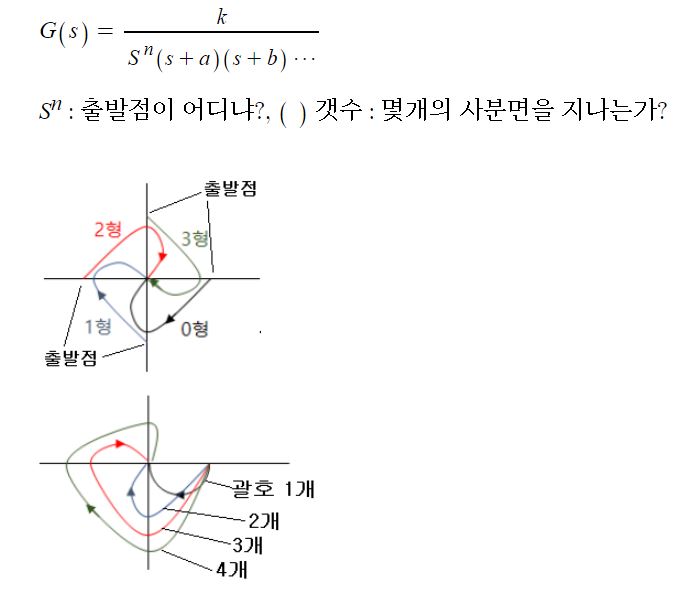
4. 형에 따른 벡터 궤적 그리는 방법
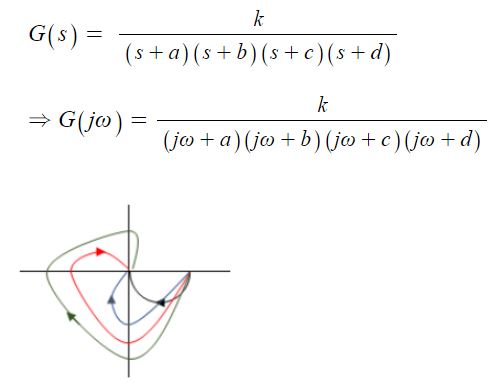
5. 보드 선도
⊙ 보도 선도 : 자동제어계에서 안정 · 불안정에 관한 정보 및 안정계에서 방법 등에 관한
도식화를 하기 위해 널리 사용되는데 이득특성곡선과 위상특성곡선 2가지 종류의 선도가 있다.
⊙ 이득특성곡선 : 주파수 변화를 대수눈금으로 log식의 "ω"를 횡축으로 하고 주파수 전달
함수 이득을 종축으로 표시하고 이득은 20log10의 진폭비로 표시한다.
⊙ 위상특성곡선 : 주파수 눈금을 대수 눈금으로 log식의 "ω"를 횡축으로 하고 주파수 전달
함수의 위상차를 종축으로 표시하고 위상차는 20log10의 진폭비로 표시한다.
◎ 위상각 Θ = G(jω) 의 각도 : 도수법 90˚ 180˚ 등
[보드 선도] ⇒ 특성 변화를 확인하기 쉽도록 그린 것
( ω : 10의 배수로 나타냄)

※ 보드 선도에는 이득, 위상 곡선이 있음
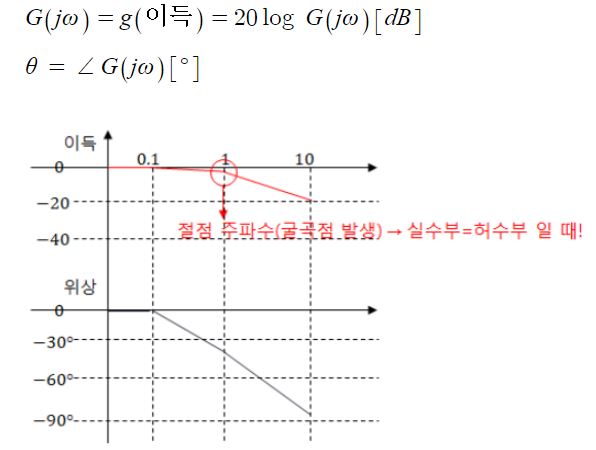
[이득]

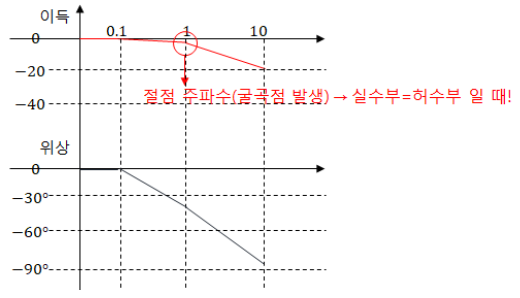
⊙ 절점 주파수 : 굴곡점이 발생하는 주파수
전달함수에서 실수부 = 허수부일 때의 주파수
⊙ 분자는 출발점
ex) 1차 지연요소 보도 선도를 예를 들면

| 각주파수 | 이 득 | 위상차 |
| ωT = 0.1 | g = 0.043 | θ = −5.7° |
| ωT = 1 | g = −3 | θ = −45° |
| ωT = 10 | g = −20 | θ = −84° |
| ωT=100 | g = −40 | θ = −90° |
6. 주파수 특성에 관한 상수 (용어 정리)
① 영주파수의 이득 M0
: 정상값 ⇒ 최종값의 정리
⊙ 영주파수의 이득 Mo (정상값) : 최종값 정리에 의하여 단위 계단 입력에 대한
정상응답은 폐회로 전달함수에서 "S = 0"으로 놓았을 때 얻을 수 있는 정상값
② 대역폭 (BW : Bandwidth)
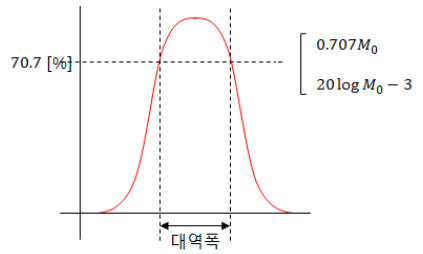
◎ 대역폭이 크면 응답속도가 빠르다
◎ 대역폭이 넓을 수록 응답속도가 빠르다
③ 공진정점 Mp(최대값)
◎ Mp가 너무 크면 오버슈트가 너무 커진다.
◎ 제어계에서 적당한 공진정점 Mp는 1.1 ~ 1.5 이다.
④ 공진주파수 ωp
◎ 공진 정점에서 일어나는 주파수
(주파수 ↑ ⇒ 주기 ↓) 주파수가 크면 주기는 작아진다.
⑤ 분리도
: 신호와 잡음을 분리하는 제어계의 특성으로서 예리한 분리특성은 공진정점(Mp)가 크다.
(분리도 ↑ ⇒ 공진정점 ↓ ⇒ 분안정하기 쉽다)
'전기인이 되는 길 > 제어공학' 카테고리의 다른 글
| [연습문제] 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
|---|---|
| 제어계의 안정도 (0) | 2023.01.10 |
| 자동제어계의 시간영역 해석 : 안정상태 (0) | 2023.01.10 |
| 자동제어계의 시간영역 해석 : 과도상태 (0) | 2023.01.10 |
| 과도 응답 (0) | 2023.01.10 |
비버리님의
글이 좋았다면 응원을 보내주세요!
