1. 시간영역 해석
⊙ 시간영역해석 : 시간이 지남에 따라서 응답(출력)이 어떻게 변하는지 알아보는 것
① 과도 응답 : 어떤 제어계에서 어떤 입력이 가해졌을 때 출력이 일정한 값에 도달하기 전까지 과도적으로 나타나는 현상
② 정상영역 (정상응답)
※ 감도 : 어떤 요소에 의해서 응답(출력)이 변하는 정도

※ 라플라스 전환
o 시간함수(t)는 해석은 쉽지만 계산이 어렵기 때문에 라플라스 변환하여 계산한 후
다시 역 라플라스 변환을 하여 전체를 해석하게 된다.

라플라스함수는 계산은 쉽지만 해석이 불가능
반대로 시간함수는 해석은 쉽지만 계산이 어려움

가. 단위계단 응답(인디셜 응답)
⊙ 입력으로 단위 계단 입력 (u(t)=1/s)을 넣었을 때의 출력
⇒ R (t) = u (t) = 1 / s
※ 단위 계단 응답(인디셜 응답)이란 ? : 입력으로 [u(t) → 1/s]을 입력시 출력을 말함


나. 임펄스 응답
라플라스 입력 '1"을 입력


다. 경사응답(등속응답, 램프(Ramp)응답)


라. 2차 지연계(R-L-C 과도응답)에서 인디셜 응답
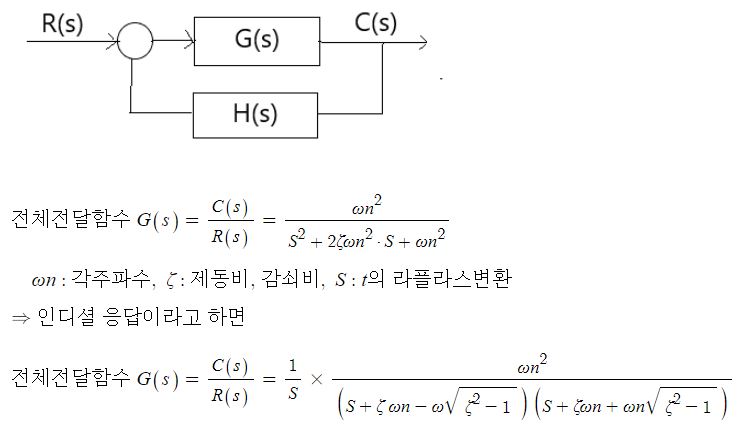
2. 제동비, 감쇠비 ζ

3. 특성방정식 - 2차 지연
※ 특성방정식 : 전체 전달함수의 분모가 "0"이 되는 방정식

① 특성방정식을 이용한 회로의 안정·불안정 해석






<1차 지연 제어계의 과도 응답>
⇒ 인디셜 응답


<2차 지연 제어계의 과도 응답>
⇒ 인디셜 응답
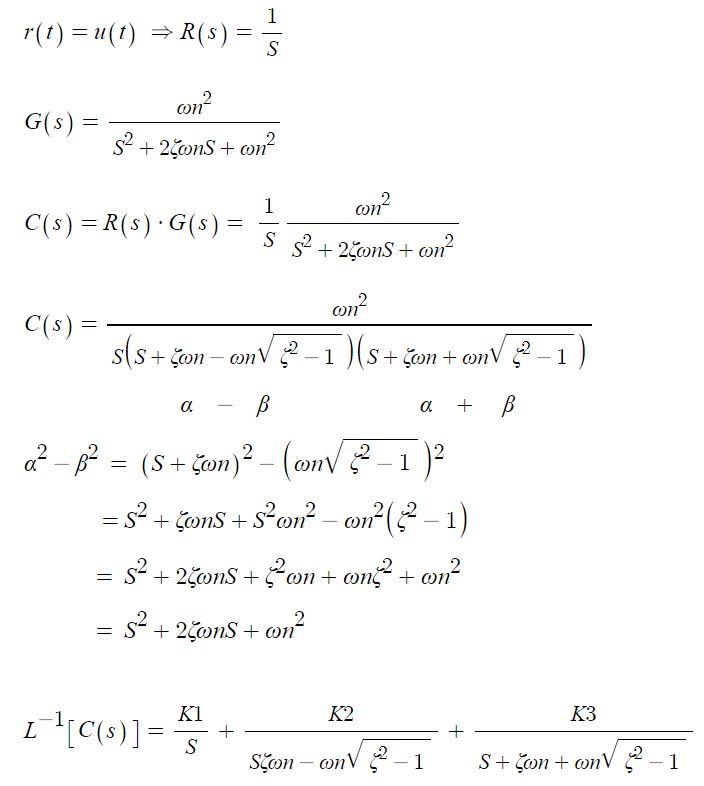

<특성방정식의 근의 위치별 과도 응답>

(4) 영점과 극점 (제6강)

① 영점 (Zero)은 분자가 "0"이고 단락상태
⊙ Z(s) 임피던스는 분자가 "0"이 되는 "S"를 영점이라 하며 회로의 단락상태를 말한다
⊙ M(s)=0 ⇒ 분자 = 0 좌표상 표시 O
② 극점(Pole)은 분모가 "0"이 되는 개방상태
⊙ Z(s) 임피던스는 분모가 "0"이 되는 "S"를 극점이라 하며 회로의 개방상태를 말한다.
⊙ M(s) = ∞ ⇒ 분모 = 0 좌표상 표시 X
5. 과도 응답의 시간 특성 - 2차 지연요소의 인디셜 응답
※ 3장 전체중 시험에 제일 잘 나옴

⊙ 오버슈트 : 응답중에 발생하는 입력과 출력 사이의 최대 편차량으로서 제어계의 안정도의 척도가 된다.
⊙ 지연시간(Delay) : 시작부터 목표값의 50%에 이르는 데 걸리는 시간
⊙ 상승시간(Rising) : 10%에서 90%에 도달하는데 걸리는 시간
⊙ 세팅(정정)시간 : 정상값의 ±5%에 들어 오기까지 걸리는 시간

'전기인이 되는 길 > 제어공학' 카테고리의 다른 글
| 자동제어계의 주파수 영역해석 (0) | 2023.01.10 |
|---|---|
| 자동제어계의 시간영역 해석 : 안정상태 (0) | 2023.01.10 |
| 과도 응답 (0) | 2023.01.10 |
| 자동제어계의, 과도응답, 시간영역해석 - 과도상태 (2) | 2021.08.25 |
| 자동제어계의 요소, 블록선도의 등가변환, 신호흐름선도 (0) | 2021.08.25 |
