아낌없이 주는 나무

1. 역적 운동량 방정식

▣ 역적이란 말은 일정한 시간 동안 힘이 쌓인다는 뜻으로 힘의 적분을 의미한다.

     배관내에 질량이 m인 물체가 dt 시간 만큼 움직인 경우에 배관내의 유속이

      V1에서 V2로 변했다고 가정을 하고 이 때 유체에 작용하는 힘을 구해 보자.​

2. 고정 평판에 작용하는 힘

​

노즐에 의하여 고정 평판에 유체를 분사했을 때 고정 평판에 작용하는 힘을 구해 보자.

위 그림에서 유동하는 유체가 고정 평판에 미치는 힘은 평판이 V2의 속도로 이동한다면

평판에 부딪힌 유체도 V2의 속도로 이동하게 되므로 다음과 같이 나타낼 수 있다.​

그런데 고정된 평판이라면 유체의 수평방향 유속 V2 = 0 되므로 다음과 같이 된다.​

여기서 부호 (-)는 유체가 흐르는 방향과 반대방향으로 힘이 작용한다는 의미이다.

또한 체적 유량 Q = A · v 이므로 이를 위식에 대입하면​

3. 경사면에 작용하는 힘

다음 그림과 같이 평면에 경사지게 노즐로 유체를 분사했을 때 작용하는 힘을 구해 보자.

위 그림에서 유체가 평판에 부딪혀 정지하고 유체에는 점성도 없다고 가정하고 작용하는 힘을 수직축 즉 중력에 의한 힘만을 구해 보면 다음과 같다.

4. 곡면에 작용하는 힘

​

다음 그림과 같이 곡관 속에 흐르는 유체가 곡면에 작용하는 힘을 구해 보자.

먼저, ①, ② 지점에서의 힘의 x축 성분, y축 성분과 속도의 x축 성분, y축 성분을 알아 보자.

먼저 속도 성분을 x축과 y축 성분으로 나누어 보면 다음과 같다.​

① 지점에서의 힘의 성분은 다음과 같다.​

② 지점에서의 힘의 성분은 다음과 같다.​

이제 곡면에 작용하는 힘의 x성분을 알아 보자. 운동량 방정식에서 힘이 작용한 만큼 운동량이 변화하므로 힘의 변화량은 운동량의 변화량과 같게 되어 다음의 식이 성립한다.

힘의 y성분을 구해 보면​

그런데 위에서 곡관의 면적이 같고 (A1 = A2), 유속이 ① 지점과 ② 지점에서 같다고 가정하면 힘의 x성분과 y성분은 다음과 같이 나타낼 수 있다.​

5. 베인 중심선이 받는 힘

​

베인이란 유체가 흐르고 있는 배관내에 수직으로 회전할 수 있도록 만들어진 날개를 말하며 일반적으로 평판을 휘어지게 만든 것을 말한다.

아래 그림과 같이 노즐에서 분사된 유체가 베인에 힘을 작용하여 베인을 회전하게 만들 때 작용하는 힘을 구하여 보자.

이 때 작용하는 x축과 y축에 작용하는 힘은 다음과 같다.​

베인 중심선에 작용하는 힘은 다음과 같다.​

6. 분류 추진 (추진력)

​

아래 그림과 같이 유체를 분출시키면 그 반발력으로 물체가 앞으로 나가게 되는데

이를 추진력, 분류 추진이라고 한다.

이 때 분류 추진으로 물체가 전진하게 되는 것은 분출되는 물체가 질량이 있고 유체의 속도가 변하는 가속도에 의하여 반발력, 즉 추진력이 생기게 되는데 이 때 작용하는 힘, 추진력은 다음과 같다.​

7. 노즐 플랜지에 작용하는 힘 (반발력)

​

어떤 배관에 유체의 속도를 높여 멀리 보내기 위해 구멍의 크기를 작게 하는 노즐을 설치하여 유체를 방사했을 때 유체가 방사하는 힘의 반발력으로 노즐의 플랜지에 힘이 작용하게 된다. 이 때 작용하는 힘을 구해 보자.

이 때 플랜지 볼트에 작용하는 힘은 다음과 같이 구할 수 있다.​

또 다른 산정식이 있는데 결과는 같다.

#운동량 #플랜지 #운동에너지 #질량유량 #체적유량 #경사면 #고정평판 #경사각 #날개각 #베인 #중심선 #추진력 #힘 #반발력 #수평 #수직

【 참고 】 공식 정리

​

가. 플랜지 볼트에 작용하는 힘​

여기서, F : 플랜지에 작용하는 힘 [N]

             γ : 물의 비중량 (9,800 [N/㎥]

             Q : 유량 [㎥/s]

              A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

              A2 : 노즐의 단면적 [㎡] = π/4·d2 [㎡]

               g : 중력 가속도 (9.8 [m/s2])

▣ 단면적 부분 계산식)​

▣ 또 다른 계산식​

여기서, F : 플랜지에 작용하는 힘 [N]

             P : 압력 [Pa = N/㎡]

              A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

              Q : 유량 [㎥/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

나. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

다. 노즐을 수평으로 유지하기 위한 힘​

여기서, F : 노즐을 수평으로 유지하기 위한 힘 [N]

              ρ : 물의 밀도 (1,000 [N·s2/m4])

              Q : 유량 [㎥/s]

              v2 : 노즐의 유속 [m/s]

라. 노즐에 작용하는 반동력​

여기서, R : 노즐에 작용하는 반동력 [N]

             P : 방수압력 [MPa]

             D : 노즐 구경 [㎜]

​

【노즐에 걸리는 반발력】 (운동량에 따른 반발력)

가. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

               v2 : 노즐의 유속 [m/s]

나. 유량​

여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

             v : 유속 [m/s]

             d : 관의 내경 [m]

다. 유량​

여기서, Q : 유량 [ℓ/min]

             d : 관의 내경 [㎜]

             P : 압력 [MPa = MN/㎡]

​

1. 옥외 소화전 1개를 개방하여 피토게이지로 방수압을 측정한 결과 0.6 [MPa]이었다.

    호스구경이 65 [㎜]이고 노즐구경이 20 [㎜]일 경우 노즐에 걸리는 반발력 [N]을 구하시오. [5점] ★★★★★

※ 노즐에 걸리는 반발력 (운동량에 따른 반발력]

      F = ρ · Q (v1 -v2) [N]

위 식을 적용할 때 유량은 지문에서 피토게이지로 측정한 압력이 주어졌으므로 다음 식을 이용하여 유량을 구한다.​

유량, 유속을 산정식에 대입하여 문제를 풀면

작용하는 힘 F =  ρ · Q (v1 -v2) [N]

                       = 1,000 [kg/㎥] × 0.01 [㎥/s] × (31.83-3.013) [m/s] = 288.17 [N]

※ 구경 (d) 값이 주어지지 않은 경우

   ⊙ 옥내 소화전 : d = 13 [㎜]

   ⊙ 옥외 소화전 : d = 19 [㎜]

​

2. 내경이 65 [㎜] 인 소방호스에 내경이 36[㎜]인 노즐이 부착되어 있다. 대기 중에 0.02 [㎥/s]의 방수량으로 방사할 경우

    노즐에 걸리는 반발력 [N]을 구하시오. [5점]  ★★★★★

노즐 반발력 F = ρ · Q (v1 -v2) [N]

                       = 1,000 [㎏/㎥] × 0.02 [㎥/s] × (19.648 - 6.027)[m/s] = 272.42 [N]

【노즐에 걸리는 반발력】 (운동량에 따른 반발력)

가. 노즐에 걸리는 반발력 (운동량에 따른 반발력)​

여기서, F : 노즐에 걸리는 반발력 (운동량에 따른 반발력) [N]

             ρ : 물의 밀도 (1,000 [N·s2/m4])

             Q : 유량 [㎥/s]

              v : 유속 [m/s]

              v1 : 소방호스의 유속 [m/s]

              v2 : 노즐의 유속 [m/s]

나. 유량​

여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

              v : 유속 [m/s]

              d : 관의 내경 [m]

​

3. 지름이 10 [㎝]인 소방용 호스에 노즐구경이 3 [㎝]인 노즐 팁이 부착되어 있다.  3 [㎥/min]의 방수량으로 대기 중에 방사

    할 경우 다음 각 물음에 답하시오. (단, 유동에는 마찰이 없는 것으로 본다) [6점] ★★★★★

 가. 소방용 호스의 평균 유속 [m/s]을 구하시오.

 나. 소방용 호스에 부착된 노즐의 평균 유속 [m/s]을 구하시오.

 다. 소방용 호스에 부착된 플랜지 볼트에 작용하는 힘[N]을 구하시오.

[풀이]

가. 소방용 호스의 평균 유속 [m/s]을 구하시오.​

나. 소방용 호스에 부착된 노즐의 평균 유속 [m/s]을 구하시오.​

다. 소방용 호스에 부착된 플랜지 볼트에 작용하는 힘[N]을 구하시오.​

※ 앞쪽 계산 먼저하고 난 후 Ans × 뒷 쪽 분수 계산을 한다.

[해설] 플랜지 볼트에 작용하는 힘

① 플랜지 볼트에 작용하는 힘​

여기서, F : 플랜지에 작용하는 힘 [N]

             γ : 물의 비중량 (9,800 [N/㎥]

              Q : 유량 [㎥/s]

             A1 : 소방호스의 단면적 [㎡] = π/4·d2 [㎡]

             A2 : 노즐의 단면적 [㎡] = π/4·d2 [㎡]

              g : 중력 가속도 (9.8 [m/s2])

② 유량 · 유속​

여기서, Q : 유량 (방수량) [㎥/s]

             A : 단면적 [㎡] = π/4·d2 [㎡]

             v : 유속 [m/s]

             d : 관의 내경 [m]

​

4. 옥내소화전설비의 노즐선단 방수압력이 0.3 [MPa]일 때 작용하는 반동력 [N]을 구하시오. [4점] ★★★​

※ 노즐 구경이 주어지지 않은 경우

   ⊙ 옥내소화전 노즐구경 : 13 [㎜]

   ⊙ 옥외소화전 노즐구경 : 19 [㎜]

[해설] 노즐에 작용하는 반동력

    반동력 F = 1.57 P · D2 [N]

여기서, R : 노즐에 작용하는 반동력 [N]

             P : 방수압력 [MPa]

             D : 노즐 구경 [㎜]

​

5. 소방시설의 가압 송수장치에서 주로 사용하는 펌프로 볼류트 펌프와 터빈 펌프가 있다.

     이들 펌프의 특징을 비교하여 다음 표의 빈칸에 유·무, 대·소, 고·저 등으로 작성하시오.  [6점] ★★★★★

[해설] 소방용 펌프

소방용 펌프는 원심펌프를 사용하며 원심펌프에는 볼류트 펌프와 터빈 펌프가 있다.

  원심펌프 - 볼류트 펌프 : 임펠러의 날개(안내깃)가 없으며 고유량, 저양정(압력)에 사용

                 - 터빈 펌프 : 임펠러의 날개(안내깃)가 있으며 저유량, 고양정(압력)에 사용

​

6. 펌프 2대를 병렬로 운전할 때와 펌프 1대를 운전할 때를 비교하여 그래프로 나타내시오.  [4점] ★★★★★

[해설] 펌프의 직렬 · 병렬 운전

7. 펌프에서 NPSH란 무엇인지 간단히 쓰고, 공동현상 (Cavitation)의 발생 한계 조건을 쓰시오. [5점] ★★★★

  가. NPSH : 물의 높이로 표시된 실제 흡입양정을 말하며, 펌프가 공동현상을 일으키지 않고 흡입가능한 압력을 물의

                     높이로 표시한 것

  나. 공동현상의 발생 한계 조건

    ① 공동현상의 발생한계 : NPSHav = NPSHre

    ② 공동현상이 발생하지 않음 : NPSHav > NPSHre

    ③ 펌프설계시 여유 : NPSHav ≥ NPSHre × 1.3

        ※ 여유율 30 % 를 둔다.

​

[해설] NPSH (흡입양정] (Net Positive Suction Head)

가. NPSH : 물의 높이로 표시된 실제 흡입 양정을 말하며 펌프가 공동현상을 일으키지 아니하고 흡입 가능한 압력을

                   물의 높이로 표시한 것

나. 펌프의 송수 조건

  (대기압 - 저항력의 합) ≥ 펌프에 의해 형성되는 진공 능력 (절대압)

  ※ 저항력 : 수면 (평상시 수면이 아닌 소요된 시간동안 물을 사용한 이후의 수면)으로 부터 펌프 임펠러 중심까지 흡입

                    과정에서의 저항력

     ① 흡입관 높이에 따른 낙차 압력

     ② 펌프 흡입측 마찰 손실 압력

     ③ 흡입관 내부에서의 포화증기압

​

다. NPSHav (유효흡입양정) = NPAHav =available

  ① 펌프의 설치조건에 따라 결정되는 펌프로 가해지는 흡입측으로 부터의 양정

  ② NPSHav (유효흡입양정)은 펌프 주변 배관의 설계에 따라 그 값이 달라진다.

​

라. NPSHre (필요흡입양정)

  ① 펌프기동에 필요한 흡입측 양정을 말하며 펌프회전에 의해 만들 수 있는 펌프 내부의 진공도에 의해 결정

  ② 펌프 제작시 결정되는 고유값 (설계시 변하지 않음)

  ③ NPSHre 가 클수록 펌프의 흡입능력은 저하

마. 공동현상의 발생 한계 조건

   ① 공동현상의 발생한계 : NPSHav = NPSHre

   ② 공동현상이 발생하지 않음 : NPSHav > NPSHre

   ③ 펌프설계시 여유 : NPSHav ≥ NPSHre × 1.3

​

8. 다음 조건을 참조하여 펌프의 유효흡입양정(NPSH)을 구하시오. [4점] ★★★★★

[조건]

  ⊙ 소화수조의 수증기압은 0.0022[MPa], 대기압은 0.1[MPa], 흡입배관의 마찰 손실 수두는 2 [m] 이다.

  ⊙ 흡상일 때 후드밸브에서 펌프까지의 수직거리가 3.8[m] 이다.

[풀이] NPSH = 10.496 - 3.8 - 2 - 0.224 = 4.172 ≒ 4.17 [m]

[해설]

  ⊙ 정압방식 (압입) : NPSH = 대 + 거 - 마 - 수 [m]

                                                대 : 대기압, 거 : 수직거리, 마 : 마찰손실, 수 : 수증기압

  ⊙ 부압방식 (흡입) : NPSH = 대 - 거 - 마 - 수 [m]

[해설] 흡입 NPSH (수면이 펌프 보다 낮을 경우)

    NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

[참고] 압입 NPSH (수면이 펌프 보다 높은 경우)

     NPSH = Ha + Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

              Ha : 대기압 환산 수두 [m]

              Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

              Hf : 마찰 손실 압력 수두 [m]

              Hv : 포화증기압 환산수두 [m]

​

9. 다음은 어느 수계 소화설비에서 송수펌프의 계통을 나타내고 있다. 다음 그림과 조건을 참조하여 펌프의 유효흡입양정

     (NPSH)을 구하시오 [4점] ★★★★★

[조건]

   ⊙ 20 [℃]에서의 수증기압은 0.001[MPa]이다.

   ⊙ 펌프의 시동 최대 송수량은 2,400 [ℓ/min] 이다.

   ⊙ 펌프 흡입 배관에서의 마찰 손실은 0.002 [MPa](최대 송수시)이다. (단, 설계기준 온도는 20[℃]이며, 대기압은

         0.1[MPa], 물의 밀도는 1 [gf/㎤]로 하며 펌프 운전시 배관에서의 속도수두는 무시한다.)

[풀이]

   NPSH = Ha - Hh - Hf - Hv [m]

              = 10.196 - 4.2 - 0.203 - 0.101 = 5.692 ≒ 5.69 [m]​

[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

     NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

10. 다음 그림을 참조하여 해발 1,000[m] 에 설치된 펌프의 유효흡입양정 [NPSH]을 구하시오. [4점] ★★★★★

[조건] ⊙ 배관의 마찰손실수두는 0.5 [m] 이다.

          ⊙ 해발 0 [m]에서의 대기압은 0.0132[MPa]이다.

          ⊙ 해발 1,000 [m] 에서의 대기압은 0.0918[MPa]이다.

          ⊙ 물의 증기압은 0.0023 [MPa]이다.

[풀이] NPSH = Ha - Hh - Hf - Hv [m]

                     = 9.36 - 4 - 0.5 - 0.235 = 4.627 ≒ 4.63 [m]​

[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

          NPSH = Ha - Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

11. 다음 그림과 조건을 참조하여 펌프의 유효흡입양정 (NPSH)을 구하시오. [4점]  ★★★★★

[조건]

  ⊙ 설계기준온도는 25 [℃] 이다.

  ⊙ 25[℃] 에서의 수증기압은 70 [㎜Hg]이다.

  ⊙ 펌프 흡입배관에서의 마찰손실수두는 0.3 [m] 이다.

[풀이]

▣ 유효흡입양정 NPSH = Ha - Hh - Hf - Hv [m]

                                      = 10.332 + 0.8 - 0.3 - 0.952 = 9.882 ≒ 9.88 [m]​

[해설] 압입 NPSH (수면이 펌프보다 높을 경우)

   NPSH = Ha + Hh - Hf - Hv [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m] (흡입 : -, 압입 : +)

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

※ 압력단위 환산

12. 펌프 흡입구에 설치된 연성계가 320[㎜Hg]일 때 이론 유효흡입수두는 몇 [m]인가? (단, 대기압은 760 [㎜Hg]이다) [4점]

        ★★★★★

[풀이] 부압방식일 때 펌프의 흡입측에 진공계 또는 연성계를 설치한다.

           진공계와 연성계의 압력은 수직거리수두, 마찰손실수두, 수증기압 수두를 모두 합한 값이 된다.

   NPSHav = Ha - (Hh + Hf + Hv) [m]

                  = 10.332 - 4.35 = 5.982 ≒ 5.92 [m]​

[해설] 흡입 NPSH (수면이 펌프보다 낮을 경우)

▣ 연성계는 부압방식(수면이 펌프보다 낮은 위치에 있는 경우)일 경우에 설치되므로 흡입 NPSH를 적용하며 연성계 압력

     에는 수직거리수두, 마찰손실수두, 포화증기압수두가 모두 포함된 값이다.

   NPSH = Ha - 연성계압력수두 (Hh + Hf + Hv ) [m]

여기서, MPSH : 유효 흡입 양정 [m]

             Ha : 대기압 환산 수두 [m]

             Hh : 낙차 압력 환산 수두 [m]

             Hf : 마찰 손실 압력 수두 [m]

             Hv : 포화증기압 환산수두 [m]

​

#플랜지 #볼트 #노즐 #반발력 #유량 #작용력 #밀도 #구경 #옥내소화전 #소화전

#운동량 #평균유속 #임펠러 #터빈 #원심펌프 #볼류트 #병렬운전 #직렬운전

#유효흡입양정 #NPSH #공동현상 #cavitation #포화증기압

【 목 차 】

1. 분자의 루이스 구조

2. 전자쌍 반발 이론

3. 결합각과 분자의 구조

4. 극성분자와 무극성 분자

5. 분자간 힘

​

1. 분자의 루이스 구조

단계 1. 분자에 있는 전체 원자가 전자의 수를 구한다.

단계 2. 원자 사이를 단일 결합으로 연결한다.

    (중심원자는 수소를 제외하고 전기음성도가 제일 낮은 원자로 정하고 2주기 원소들을

    팔전자 규칙을 만족하도록 결합수를 정한다. 붕소(B)는 예외적으로 전자 결핍이 되고,

     3주기 이상의 원소들은 d오비탈의 영향으로 확장된 팔전자 규칙을 따르기도 한다)

단계 3. 단계1 에서 구한 전체 원자가 전자 수로 부터 결합에 이용한 원자가 전자수를 뺀

     나머지 전자들을 전기 음성도가 큰 말단 원자에 할당하여 팔전자 규칙을 정한다.

단계 4. 단계 3 이후에도 할당되지 않고 남은 전자가 있다면 중심 원자에 배치한다. (중심

     원자가 3주기 이상이면 전자를 8개 보다 많이 가질 수 있다!!!)

단계 5. 만약 중심원자가 팔전자 규칙을 만족하지 못한다면 다중결합을 만든다.

​

▣ 14족 C - 4, 15족 N - 3, 16족 O - 2, 17족 F - 1 이 있다면 이 때 중심원자를 전기

      음성도가 제일 낮은 우너자로 정한다는 것은 위 원소중에서는 탄소(C)가 전기음성도가

      제일 낮으니까 결합을 제일 많이 할 수 있는 원소를 가운데 넣는다.

▣ 팔전자 규칙을 따르는데 예외로 붕소(B)는 최외각 전자껍질의 전자수가 3개 인데 최외

     각 전자가 6개만 있어도 안정을 취하는 특이한 원소이다.

  예 ) SF4

        SF4 ⇒ S : 6개 F4 : 7 × 4 =28, ∴ 6 + 28 = 34 (최외각 전자 합계)

   이 3 원소를 단일결합을 시키자. 단일결합이 2개 이므로 2×2=4, 4개의 전자를 사용했으

   므로 10-4=6, 6개 전자가 남았다. 남은 6개 전자는 전기음성도가 가장 큰 원소를 주라고

   했고 전기음성도는 F-O-N 순이므로 질소(N)에 전자를 배치한다.

   질소(N)에 전자를 배치하고 보니 탄소(C)는 결합수가 4개이어야 하는데 2개 밖에 없으

   므로 질소(N)의 최외각 전자 4개를 이용하여 탄소(C)와 질소(N)간에 공유결합을 한다.

   이렇게 공유 결합을 하면 탄소(C)와 질소(N)간에 3중 결합을 하게 되고 탄소(C)와 질소

   (N) 모두 팔전자 규칙을 만족 시키게 된다.

​

◈ CO2의 분자구조에 대하여 알아 보자.

   CO2 : 원자가 전자수는 C - 1×4, O - 6×2, 합하면 4+12 = 16개이다.

   전자결합수는 C - 4, O - 2 이므로 결합수가 많은 탄소(C)를 중심에 둔다.

   결합수가 2개 이므로 2×2=4, 전자 4개를 사용했으므로 16-4=12개가 남았다.

    전기음성도가 높은 산소(O)에 남은 전자 12를 산소(O)에 배치하여 팔전자 규칙을 만족하

    자. 그런데 이렇게 하면 탄소(C)는 팔전자 규칙을 만족하지 못하여 2개의 산소(O)의 전자

    2개씩 4개를 이용하여 탄소(C)와 산소(O)간 공유결합을 하면 탄소(C)와 산소(O)는 이중

    결합이 되고 둘 다 팔전자 규칙을 만족하고 탄소(C)의 결합수도 맞출 수 있다.

◈ CH4O의 분자구조에 대하여 알아 보자.

    CH4O : 원자가 전자수는 C-4×1, H-1×4, O - 6×1, 합하면 4+4+6 = 14개이다.

    전자결합수는 C - 4, H - 1, O -2 이므로 결합수가 많은 탄소(C)를 중심에 둔다.

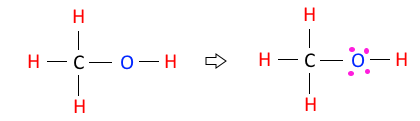
    단일 결합이 5개이므로 전자 5×2=10개를 사용했으므로 14-10은 4개 남았다.

    산소의 전기음성도가 가장 크므로 남은 전자 4개를 산소(O)원자에 배치한다.

    이렇게 하면 탄소(C), 수소(H), 산소(C) 모두 결합규칙을 만족하게 된다.

​

◈ C2H2의 분자구조에 대하여 알아 보자.

    C2H2 : 원자가 전자수는 C-4×2, H-1×2, 합하면 8+2 = 10개이다.

    전자결합수는 C - 4, H - 1 이므로 결합수가 많은 탄소(C)를 중심에 둔다.

   단일 결합수가 3개이므로 3×2=6, 6개의 전자를 사용하였으므로 10-6=4, 4개의

   전자가 남는다. 남은 4개 전자를 전기음성도가 큰 탄소(C) 원소에 각각 2개씩을

   배치하면 탄소의 팔전자 규칙을 만족한다. 그런데 탄소의 결합수는 4개이므로

   부족한 4개를 탄소(C) 원자의 최외각 전자 2개씩을 활용하여 탄소(C)-탄소(C)의

   공유결합을 하면 3중 결합을 하게 된다.

​

가. Review : 전자구름 배열 및 분자 모형을 결정하는 단계

   ① 분자 또는 다원자 이온의 Lewis 구조를 그린다.

   ② 중심원자의 전자구름수를 센다.

   ③ VSEPR 모델을 적용하여 전자구름의 기하구조를 결정한다.

   ④ 원자핵 사이를 연결하여 분자의 모양을 결정한다.

​

[루이스 분자 구조와 분자의 모양과 어떤 관계가 있는지 알아 봅시다]

가. CH2O

 ◈ CH2O의 분자모양에 대하여 알아 보자.

      CH2O : 원자가 전자수는 C-4×1, H-1×2, O-6×1 합하면 4+2+6 = 12개이다.

      전자결합수는 C - 4, H - 1, O-2 이므로 결합수가 많은 탄소(C)를 중심에 둔다.

    단일 결합이 3개 이므로 3×2=6, 6개 전자를 사용했으므로 12-6=6, 6개의 전자가 남고

    남은 전자 6개를 전기음성도가 높은 산소(O)에 배치한다. 그런데 탄소의 결합수 4개를

    맞추기 위해 산소의 최외각 전자 2개를 탄소(C)와 공유결합을 하게 되면 탄소(C)와 산소

    (O)는 2중 결합을 하게 된다.

​

    여기에서 중심원자 탄소(C)를 중심으로 전자구름을 보면 중심원자 탄소 주위에 이렇게

    이중결합- 뚱뚱한 전자결합이 하나 있고 단일결합 - 가느다란 전자구름이 2개가 있다.

    결국 탄소 주위에는 3개의 전자구름이 있다. 이들 전자 구름간에는 반발력이 있게 된다.

    이 전자구름간에는 반발력이 작용하여 가장 멀리 있으려고 하고 가장 멀리 있으려면

    평면 삼각형 모양이 되고 아래 그림과 같이 있게 된다.

    전자구름의 기하구조를 결정하려고 하는데 이들간에는 서로 멀리 있으려 하니까 평면

    삼각형 모양이 되고 이 때 이 분자의 모양은 언제나 전자구름을 이렇게 배열해 놓고

    분자의 모양은 원자의 핵과 핵 사이를 결합하는 것이 분자 모양이다.

    따라서 CH2O의 분자모양은 평면 삼각형 모양이 된다.

​

예제) 다음 각 화합물 들에 대해 전자구름의 기하 구조와 분자모양을 정하시오.

  [ SO3 와 ICl4- ]

  ▣ SO3

       SO3 의 원자가 전자수는 S- 6, O3 - 6×3 합하여 6 + 18 = 24 이다.

       황(S)보다 산소(O)가 전기음성도가 크므로 S보다 O가 위에 있게 되므로 S를 중심에 둔다.

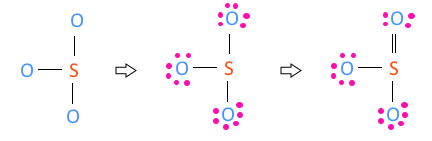
    단일 결합이 3개 이므로 3 × 2 =6, 6개 전자를 사용하였으므로 24 - 6 = 18, 18개의 전

    자가 남는다. 남은 전자 24개를 전기음성도가 높은 높은 산소(O) 원자 3개에 배치한다.

    그런데 이렇게 되면 황(S)은 최외각 전자가 6개 밖에 되지 않는다. 이를 해결하기 위하여

    산소(O) 원자 3개 중 하나의 원자의 최외각 전자 2개를 이용하여 황(S)와 산소(O)간의

    공유결합을 하는데 사용한다. 따라서 황(S)와 산소(O)간에 이중결합 하나가 생긴다.

    이런 구조상에서 분자의 모양을 결정하라 하면 분자 모양은 전자의 구름형태를 본다고

    했다. 중심원자의 황(S)를 중심으로 보면 전자구름은 3개가 된다. 전자구름 간에 반발력

    이 있어 서로 멀리 떨어져 있으려고 하니까 평면 삼각형 모양이 된다.

    즉, 분자모양은 원자 핵과 핵 사이의 평면 삼각형이 된다.

​

▣ ICl4-

    ICl4- 의 원자가 전자수는 I 아이오딘에 Cl 이 4개 있고 마이너스(-) 이온이다.

    이런 경우 아이오린이 마이너스(-), 아이오딘은 제일 바깥 껍질의 전자가 7개이다. Cl은

    원래 제일 바깥 껍질의 전자가 7개인 원소가 4개 있다. 그런데 이것이 마이너스(-) 이온화

    되었다고 하니까 전자가 하나 더 있는 것이다.

    그러므로 원자가 전자수는 C-7, Cl4 - 7×4+1 합하여 7+29 = 36개가 된다.

    여기에서 I 와 Cl 을 비교해 보면 전기 음성도가 F - Cl - Br - I 순이므로 Cl이 I 보다 전기

    음성도가 크다. 그러므로 I 가 중심원자가 되어야 한다.

    남은 전자 28개를 전기 음성도가 높은 Cl에 배치를 하면 28-24=4개의 전자가 남게 된다.

    그런데 남은 전자 4개는 마이너스(-) 이온에 의하여 들어 온 전자는 중심원자에 들어가야

    한다. 왜냐하면 Cl은 7개가 단일 결합하는 방법 밖에 없기 때문이다.

    I 와 Cl간 단일 결합을 하면 결합수가 4개 이므로 4×2=8, 8개의 전자를 사용했으므로

    36-8=28개의 전자가 남게 된다.

    남은 전자 28개를 전기음성도가 높은 염소(Cl) 원자 4개에 배분한다.

    이제 남은 전자 4개를 중심원자 아이오딘(I) 에 배치한다. 아이오딘(I) 은 5주기 원자이므

    로 중심원자에 전자를 배치할 수 있다. 3주기 이상의 원소에는 전자가 들어 갈 영역이 넓어

    서 남은 전자를 중심 원자에 줄 수 있다.

    전자 구름을 보면 평면 사각형 전자구름이 있고 또한 아이오딘(I) 위 아래에 전자구름이 있

    는 모양이 된다. 아이오딘(I) 위 아래에 전자구름은 분자 모양을 나타낼 때는 나타나지 않는

    다. 분자모양은 원자핵과 핵 사이의 관계를 나타내는 것이기 때문이다.

    따라서 분자 모양은 평면 사각형 모양이 된다.

나. 중심원자 주위의 전자구름 배열

▣ 분자의 모양은 위 그림과 같은 모양이다. 중심원자를 중심으로 주변에 결합이 2개 있으

    면 직선형 모양이 되고 3개면 삼각평면형, 4개면 정사면체, 5개면 3개는 평면 삼각형을

    이루고 2개는 위·아래 쪽으로 삼각뿔 형태를 이룬다. 삼각쌍뿔의 경우에는 평면삼각형

    의 경우 내각이 120°를 이루는데 위·아래 삼각뿔은 평면과 90°의 각도를 이룬다.

    따라서 평면은 넓게 퍼져 있어 반발력이 적게 작용한다. 이렇게 전자구름의 반발력이 차

    이가 있어 결합각이 큰 곳에 비공유 전자쌍이 있기 좋고 더 좋은 것은 위·아래 각도가

    90° 에 들어가도 좋다. 이것이 바로 '전자쌍 반발이론'이다.

​

다. 전자구름 배치 vs 분자 모양

  ▣ 중심 원자 주위의 전자구름 (결합과 고립 전자쌍 또는 홀전자)의 배열인 전자구름 기하

      구조와 결합된 원자의 배열인 분자의 모양은 다르다 !!!)

  ▣ 분자 모양의 결정법

    ① 분자의 루이스 구조를 그린다.

    ② 중심원자 주위의 전자구름을 VSEPR 이론에 맞춰 배치한다.

    ③ 분자를 구성하는 원자의 핵들을 연결하여 분자모양을 결정한다.

    ※ 전자 구름이 고립 전자쌍인 경우에는 결합각이 작아져서 반발력이 커질 수 있다.

CH4 의 경우에는 전자구름 4개가 모두 단일 결합으로 정사면체로 결합각이 모두 109.5°

로 동일하다. NH3는 삼각뿔 형태로 위에 비공유 전자쌍이 있어 가느다란 전자쌍이 비공유

전자들을 끌어 당겨 결합각이 109.5°에서 107°로 줄어든다.

H2O는 넓게 펼쳐진 비공유 전자쌍이 2개가 있다. 비공유 전자쌍은 공유전자쌍에 끌어 당

겨져서 결합각이 104.5°로 줄어든다.

분자의 모양이 굽은 모양이 되는 이유는 분자의 모양은 핵과 핵 사이를 연결하는 선이다.

비공유 전자쌍이 있는 곳은 전자 구름이 있어서 이 공간에는 다른 전자가 들어 오지 못하게

하는 공간의 영역을 나타내지만 실제 분자의 모양은 핵과 핵 사이를 연결한 선이 분자의

모양이기 때문에 연결선 2개가 만들어지는 굽은 모양의 평면이 존재하게 되는 것이다.

​

3. 결합각과 분자 구조

가. 5개의 전자구름 : PCl5, SF4, ClF3, I3-

 ◈ PCl5

   인(P)은 최외각 전자가 5개, 염소(Cl)는 최외각 전자가 7개인데 원자가 5개 이므로

   전체 최외각 전자수는 5 + 7 × 5 = 40 개가 된다.

   결합수가 많은 P를 중심에 둔다.

  ▣ 5개의 전자구름은 평면 삼각형 위·아래에 전자구름이 있는 형태이다. 이런 분자구조를

      '삼각쌍뿔'이라고 한다.

  ▣ 결합각 90°가 120° 보다 반발력이 더 세게 작용하므로 결합각 90°에 있는 염소(Cl)이

       더 멀어져서 "정몇몇면체"가 아니고 삼각쌍뿔이라고 한다.

​

◈ SF4

   S는 최외각 전자가 6개이고 F는 4개 이므로 결합수 4개를 하면 S의 비공유 전자 2개가

    남는다. 따라서 비공유 전자쌍이 1개가 남게 된다.

     전자쌍 중 가느다란 공유전자쌍 보다 뚱뚱한 비공유 전자쌍이 반발력이 크다.

   비공유 전자쌍이 큰 반발력으로 공유 전자쌍을 옆으로 밀어서 치우친 전자쌍이 된다.

   이런 모양을 '시소형'이라고 한다.

​

◈ ClF3

   최외각 전자가 Cl은 7개이고 F가 3개가 결합하니까 단일결합은 3개이고 Cl의 비공유

   전자쌍은 2개가 된다.

  평면 삼각형에 있는 비공유 전자쌍 2개가 공유 결합 전자 구름을 밀게 된다. 분자 모양은

  원자 핵과 핵 사이를 연결하는 것이므로 공유 전자쌍 연결선이므로 굽은 T자형이다.

​

◈ I3-

  I는 최외각 전자가 7개인데 마이너스(-) 이온이므로 전자가 하나 더해져서 8개가 된다.

  이것은 I- 와 I2 가 결합한 형태가 된다. 따라서 단일 결합 1개, 비공유 전자쌍이 3개 된다.

  이 분자 모양은 평면 4각형에 위·아래에 수소(H) 단일결합이 있고 모두 결합각이 90°가

  된다. 분자 모양은 정팔면체가 된다.

​

◈ BrF6

  Br은 최외각 전자가 7개이며 F5 와 결합을 하니까 단일결합이 5개, 비공유 전자쌍이 1개가 있다.

  비공유 전자쌍은 위·아래 어디에 두어도 되는데 아래에 표기하는 것이 편하여 아래에 둔다.

  이 분자 구조는 사각뿔이라고 하는데 비공유 전자쌍이 평면 사각형 공유전자쌍 구름을

  위로 밀어 올리게 된다.

​

◈ XeF4

   Xe는 제논이라고 해서 비활성 기체이다.

   비활성 기체 (He, Ne, Ar, Kr, Xe, Rn) 중에서 He, Ne, Ar은 안정된 기체로 반응을 하지

   않지만 Kr은 전자껍질이 4개, Xe은 전자껍질 5개, Rn은 전자껍질 6개이어서 플로우린

   처럼 반응성이 큰 물질과는 반응을 하게 된다.

   제논(Xe)은 최외각 전자가 8개이고 F4와 결합을 하므로 단일 결합이 4개, 비공유 전자쌍

   이 2개가 된다.

    분자 모양은 평면 사각형이고 위·아래에 비공유 전자구름이 있게 된다.

​

다. 분자유형과 기하구조의 관계

라. 이상적인 결합각과 편차

  ▣ 특정 전자구름은 다른 전자 구름 보다 이웃전자들과 더 잘 반발하기 때문에 이상적인

       결합각에서 벗어날 수 있음

  ▣ 고립 전자쌍은 결합전자쌍 보다 더 많은 공간(space)을 차지하여 반발력이 더 큼

  ▣ 다중 결합은 더 높은 전자밀도를 갖기 때문에 단일 결합 보다 반발력이 큼

4. 극성 분자와 무극성 분자

가. 분자의 기하구조와 극성

  ▣ 쌍극자 모멘트는 동일한 화학식을 갖지만 원자의 기하구조가 다른 분자(기하이성질체)

      를 구별하는 기준이 될 수 있다.

  예) 다이클로로 에틸렌 (C2H2Cl2)

  ※ 수소결합은 분자간의 결합이지만 마치 플러스(+), 마이너스(-) 이온 결합과 같이

     분자간의 결합이 매우 강하다.

  ▣ 수소가 전기음성도가 매우 큰 원소 (F,O,N) 들과 결합하면 전기음성도가 큰 F,O,N

      원자가 수소의 전자를 당기므로 수소의 양성자 값이 +0.85에서 +0.9 정도가 된다.

      이런 수소 옆에 비공유 전자쌍을 갖고 있는 F, O, N이 있으면 F, O, N의 마이너스(-)

      는 -0.8 ~ 0.85 정도가 된다. 이 때 수소(H)와 F, O, N이 서로 당겨져서 결합하는 것을

      수소결합이라고 하는데 이는 마치 이온 결합처럼 결합의 강도가 매우 강하다.

​

라. 분산력

  ▣ 분산력의 크기는 분자내에서 전자들이 얼마나 유동적인가에 의존

  ▣ 큰 분자가 더 쉽게 편극될 수 있어 더 큰 순간 쌍극자와 유발 쌍극자를 가지며 전체적으

      로 더 큰 분자간 인력을 나타냄

  ▣ 분산력은 무극성 분자들 사이에만 작용하는 것이 아니라 모든 분자들 사이에서 작용