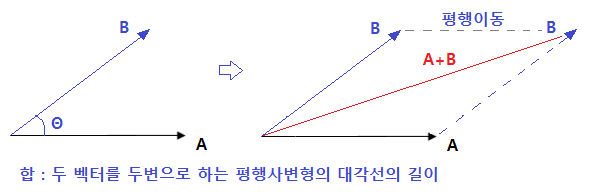
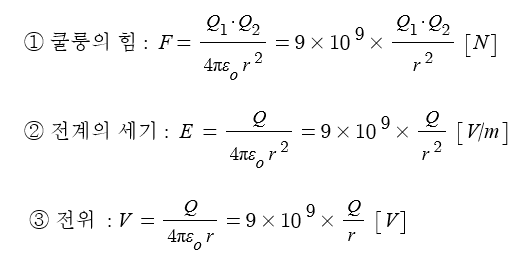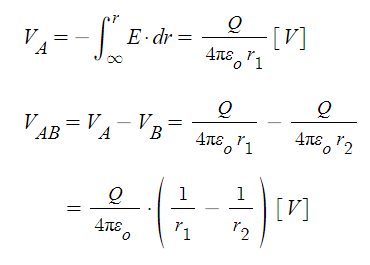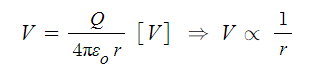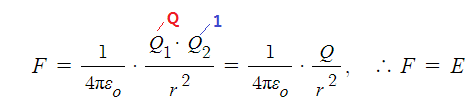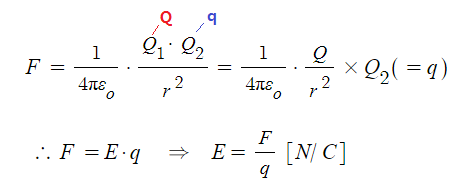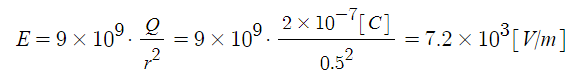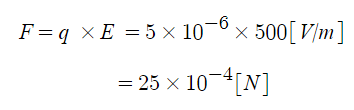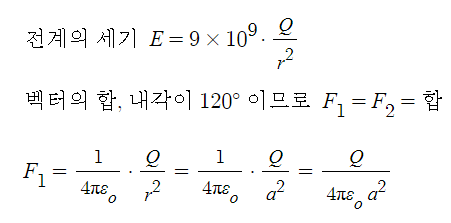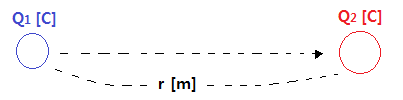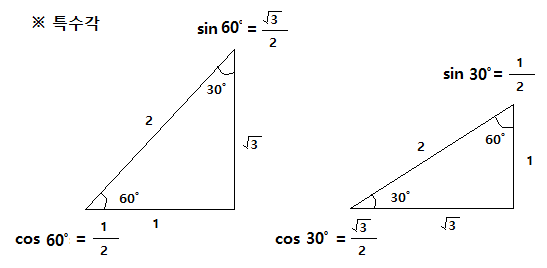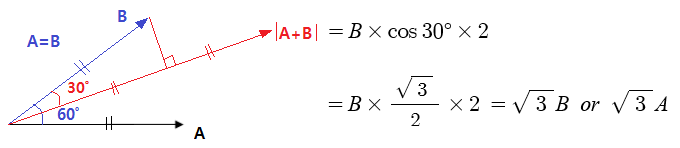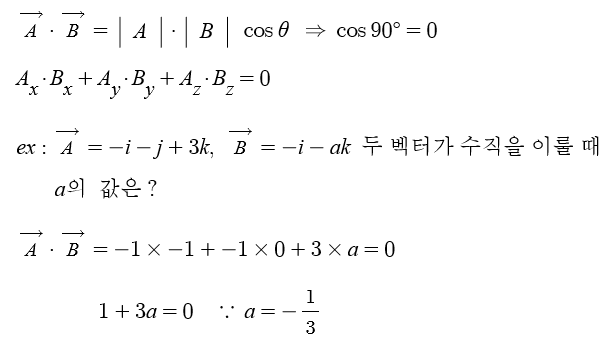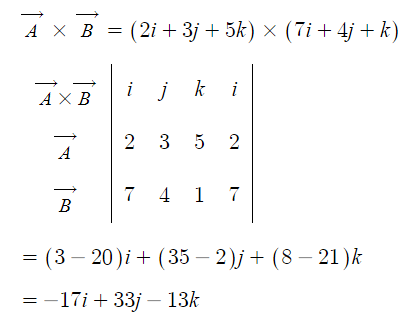1. 전기력선
▣ 전기력선
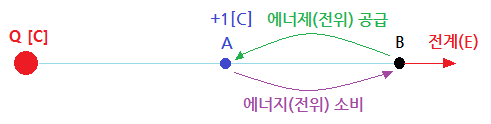
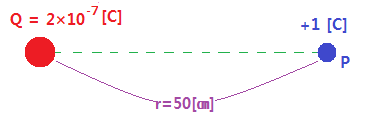
⊙ 전계(E)내에서 단위 정전하 (+1[c])을 놓았을 때 이 단위 정전하가 받는
힘의 방향을 시각적으로 표현하기 위하여 가상한 선을 말한다.

가. 전기력선의 성질
① 전기력선은 양전하에서 시작하여 음전하에서 끝난다.

② 전하가 없는 곳에서는 전기력선의 발생과 소멸은 없다. (즉, 연속적이다)
③ 전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다.

④ 두 전기력선은 서로 교차하지 않는다.
⑤ 전기력선은 그 자신만으로 폐곡선이 되지 않는다.
⑥ Q[C] 의 전하에서는 Q/εo 개의 전기력선이 나온다.

⑦ 전기력선의 밀도
⊙ 어느 점에서의 전기력선의 밀도를 그 점의 전계의 세기로 정의한다.
⊙ 전기력선이 어느 공간에 +1[C]의 양전하를 놓았을 때 받는 힘을 나타내기 위한 선이므로
이러한 전기력선이 얼마나 많이 있는지 적게 있는지를 나타내는 밀도는 전계의 세기를
나타낸다는 것은 당연한 말이다.

나. 전기력선의 방향
▣ 어느 점에서의 전기력선의 접선 방향을 그 점에서의 전계(E)의 방향으로 정의
※ 접선 : 수평방향, 법선 : 수직방향

⑨ 전기력선은 등전위면과 수직이다.
⑩ 전기력선은 도체 표면에 수직으로 출입한다.
⑪ 도체 내부에는 전기력선이 존재하지 않는다.
2. 등전위면
1. 등전위면
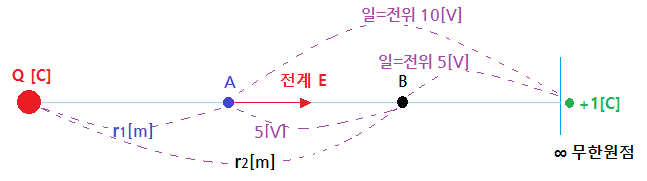
▣ 전계내에서 전위가 같은 점을 연결하여 얻어지는 면
⊙ 점전하로 부터 받는 힘의 세기는 그 점전하로 부터 거리의 제곱에 반비례하므로
등전위면은 점전하로 부터 같은 거리에 위치하게 된다.

가. 등전위면의 성질
① 서로 다른 전위를 가진 등전위면은 교차하지 않는다.
② 등전위면과 전기력선은 반드시 수직으로 교차한다.
③ 전기력선은 전위가 높은 곳에서 낮은 곳으로 향한다.
④ 등전위면은 폐곡면이다.
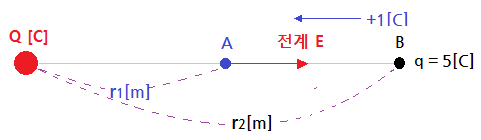
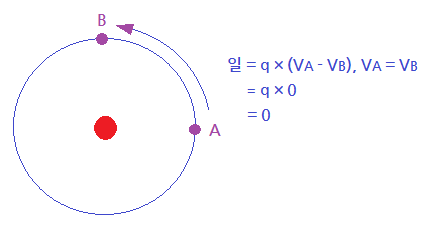
⑤ 등전위면을 따라 전하를 운반하는데 필요한 일은 영"0"이다.
3. 대전된 도체의 성질
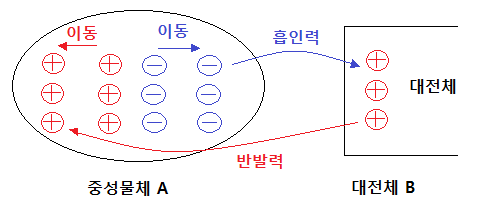
① 대전된 도체의 전하는 도체 표면에만 존재한다.
※ 도체 내부에는 전하가 없다.
(대전체는 서로간 반발력이 작용하므로 밖으로 밀려나 바깥쪽에 대전체가 있다)
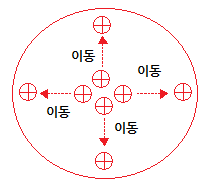
② 도체 내부의 "전계의 세기"는 "영(0)"이다.
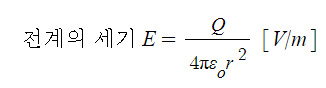
③ 도체 표면 및 내부의 전위는 등전위다.
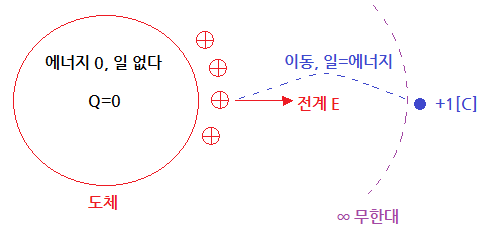
④ 도체 표면에서 전기력선은 도체표면에 수직으로 교차한다.
※ 도체 표면은 등전위면이다.
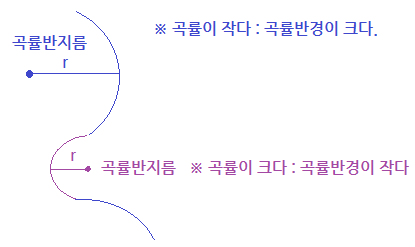
⑤ 도체 표면에서 전하밀도는 곡률반경이 클 수록 (곡률이 작을 수록) 작아진다
【벡터의 미분】
1. 미분의 기본 법칙
▣ 미분방정식은 다음과 같다.

미분
▣ 변수와 미분계수가 같을 때만 미분이 가능하다.

▣ 미분의 기본방식은 다음과 같다.


▣ 편미분 : 미분계수와 변수가 다른 경우에도 미분을 가능하게 한다.
① 변수와 미분계수가 달라도 미분이 가능하다.
② 다변수 함수에서 한개의 변수에 대해서만 미분을 한다.
③ 미분계수와 상관없는 변수들은 상수 취급을 한다.
④ 나머지는 "일반미분"과 같다.
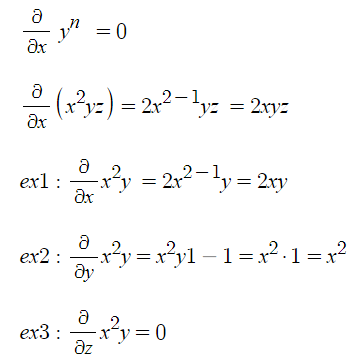
2. 미분 연산자 : 명령어 (컴퓨터)
가. ▽
① 명칭 : "나블라", "del 델" ⇒ 편미분 연산자
② 표현

③ 결과 : 벡터 ⇒ i, j, k 로 표현
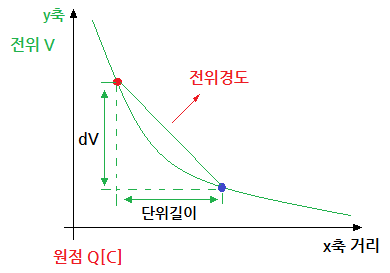
나. grad
① 명칭 : gradient
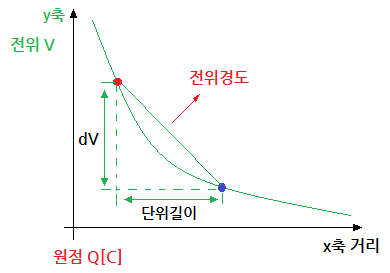
② 의미 : 기울기, 경사, 경도, 구배
③ 용도 : "전위 V"의 기울기를 구할 때
④ 표현 : " ▽"와 같다.
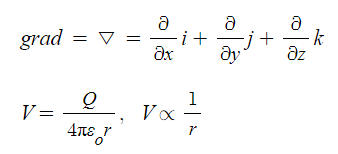
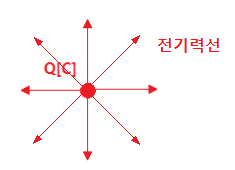
다. div
① 명칭 : 다이버젼스 divergence
② 의미 : 발산
③ 용도 : 전기력선이 발산하는 모양을 수식화할 때 사용
④ 표현 (연산자) : ▽ · (나블라 도트)
⑤ 결과 : 스칼라
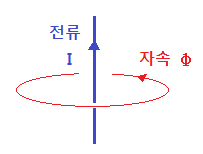
라. rot, curl, Rotation
① 명칭 : 로테이션, 커얼
② 의미 : 회전 (Rotation)
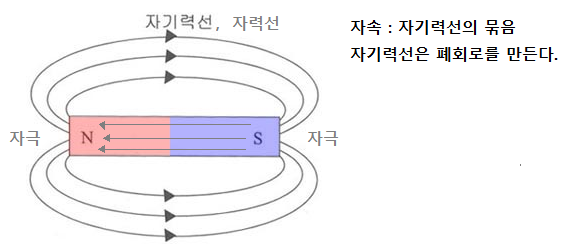
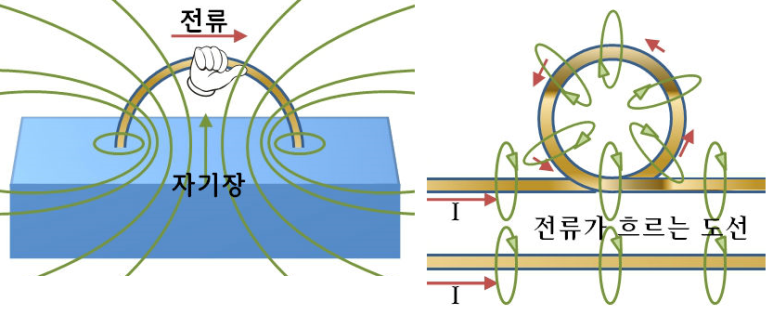
③ 용도 : 자속이 회전하는 모양을 나타낸다.
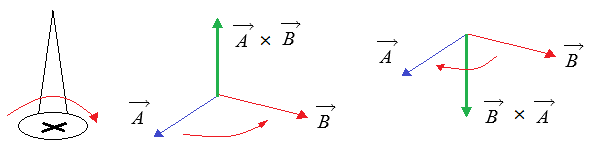
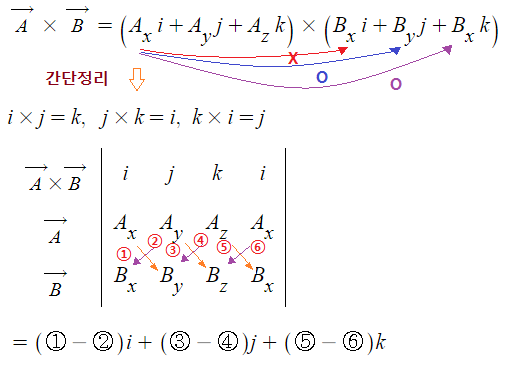
④ 표현 (연산자) : ▽ × (나블라 크로스)
⑤ 결과 : 벡터 i, j, k 로 표현
【벡터의 미분 결과】
① ▽, grad, rot (curl) ⇒ 벡터 : 방향을 나타내는 i, j, k 로 표현
② div (▽·) ⇒ 스칼라 (내적)
가. 스칼라 기울기 = 전위의 기울기

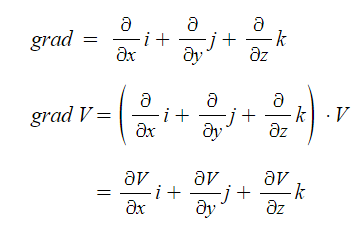
예제1. 전위함수 V = x^2yz 일 때 한점 (1,2,3)에서 grad V를 구하시오.
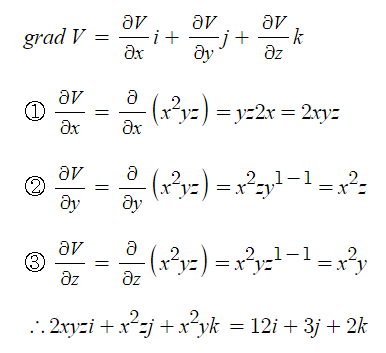
'전기인이 되는 길 > 전자기학' 카테고리의 다른 글
| 유전율과 전계의 세기 (0) | 2021.11.11 |
|---|---|
| 벡터의 미분, 전위경도, 발산, 회전의 예제 - 전자기학 (0) | 2021.11.06 |
| 전자기학 - 전위 [V] (0) | 2021.10.27 |
| 전계 및 전계의 세기 (0) | 2021.10.27 |
| 대전, 대전체, 쿨룽의 힘 (5) | 2021.10.27 |