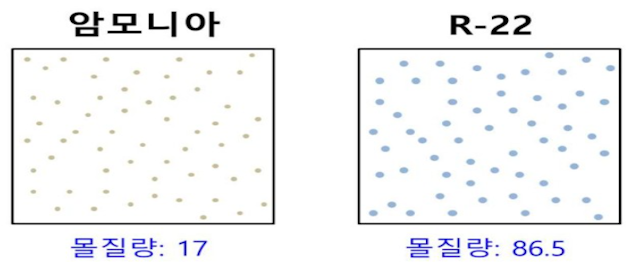
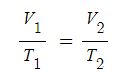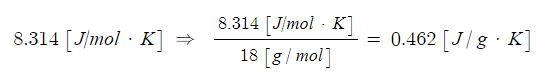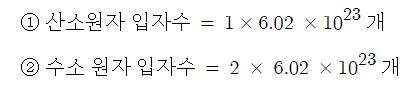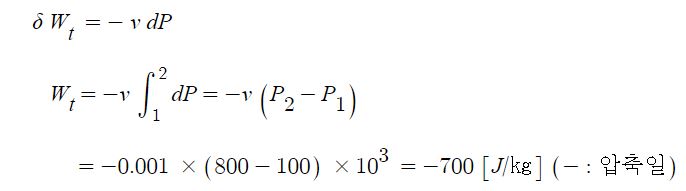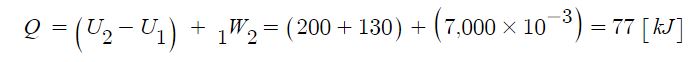Ⅰ. 위험물 저장 기준
1. 저장·취급의 공통기준
① 제조소등에서 허가 및 신고와 관련되는 품명 외의 위험물 또는 이러한 허가 및 신고와 관련되는 수량 또는 지정수량의
배수를 초과하는 위험물을 저장 또는 취급하지 아니하여야 한다.
② 위험물을 저장 또는 취급하는 건축물 그 밖의 공작물 또는 설비는 당해 위험물의 성질에 따라 차광 또는 환기를 실시
하여야 한다.
③ 위험물은 온도계, 습도계, 압력계 그 밖의 계기를 감시하여 당해 위험물의 성질에 맞는 적정한 온도, 습도 또는 압력을
유지하도록 저장 또는 취급하여야 한다.
④ 위험물을 저장 또는 취급하는 경우에는 위험물의 변질, 이물의 혼입 등에 의하여 당해 위험물의 위험성이 증대되지
아니하도록 필요한 조치를 강구하여야 한다.
⑤ 위험물이 남아 있거나 남아 있을 우려가 있는 설비, 기계·기구, 용기 등을 수리하는 경우에는 안전한 장소에서 위험물
을 완전하게 제거한 후에 실시하여야 한다.
⑥ 위험물을 용기에 수납하여 저장 또는 취급할 때에는 그 용기는 당해 위험물의 성질에 적응하고 파손·부식·균열 등이
없는 것으로 하여야 한다.
⑦ 가연성의 액체·증기 또는 가스가 새거나 체류할 우려가 있는 장소 또는 가연성의 미분이 현저하게 부유할 우려가 있는
장소에서는 전선과 전기기구를 완전히 접속하고 불꽃을 발하는 기계·기구·공구·신발 등을 사용하지 아니하여야 한다.
⑧ 위험물을 보호액중에 보존하는 경우에는 당해 위험물이 보호액으로부터 노출되지 아니하도록 하여야 한다.
2. 위험물의 유별 저장·취급의 공통기준
① 제1류 위험물은 가연물과의 접촉·혼합이나 분해를 촉진하는 물품과의 접근 또는 과열·충격·마찰 등을 피하는 한편,
알카리금속의 과산화물 및 이를 함유한 것에 있어서는 물과의 접촉을 피하여야 한다.
② 제2류 위험물은 산화제와의 접촉·혼합이나 불티·불꽃·고온체와의 접근 또는 과열을 피하는 한편, 철분·금속분·마그네
슘 및 이를 함유한 것에 있어서는 물이나 산과의 접촉을 피하고 인화성 고체에 있어서는 함부로 증기를 발생시키지
아니하여야 한다.
③ 제3류 위험물 중 자연발화성물질에 있어서는 불티·불꽃 또는 고온체와의 접근·과열 또는 공기와의 접촉을 피하고,
금수성물질에 있어서는 물과의 접촉을 피하여야 한다.
④ 제4류 위험물은 불티·불꽃·고온체와의 접근 또는 과열을 피하고, 함부로 증기를 발생시키지 아니하여야 한다.
⑤ 제5류 위험물은 불티·불꽃·고온체와의 접근이나 과열·충격 또는 마찰을 피 하여야 한다.
⑥ 제6류 위험물은 가연물과의 접촉·혼합이나 분해를 촉진하는 물품과의 접근 또는 과열을 피하여야 한다.
3. 저장의 기준
① 저장소에는 위험물 외의 물품을 저장하지 아니하여야 한다. 다만, 다음 1에 해당하는 경우에는 그러하지 아니하다
㉮ 옥내저장소 또는 옥외저장소에서 다음의 규정에 의한 위험물과 위험물이 아닌 물품을 함께 저장하는 경우. 이 경우
위험물과 위험물이 아닌 물품은 각각 모아서 저장하고 상호간에는 1m 이상의 간격을 두어야 한다.
㉠ 위험물(제2류 위험물 중 인화성고체와 제4류 위험물을 제외한다)과 영 별표 1에서 당해 위험물이 속하는 품명란에
정한 물품(동표 제1류의 품명란 제11호, 제2류의 품명란 제8호, 제3류의 품명란 제12호, 제5류의 품명란 제11호 및
제6류의 품명란 제5호의 규정에 의한 물품을 제외한다)을 주성분으로 함유한 것으로서 위험물에 해당하지 아니하
는 물품
㉡ 제2류 위험물 중 인화성고체와 위험물에 해당하지 아니하는 고체 또는 액체로서 인화점을 갖는 것 또는 합성 수지
류(「소방기본법 시행령」 별표 2 비고 제8호의 합성수지류를 말한다) 또는 이들중 어느 하나 이상을 주성분으로
함유한 것으로서 위험물에 해당하지 아니하는 물품
㉢ 제4류 위험물과 합성수지류등 또는 영 별표 1의 제4류의 품명란에 정한 물품을 주성분으로 함유한 것으로서 위험
물에 해당하지 아니하는 물품
㉣ 제4류 위험물 중 유기과산화물 또는 이를 함유한 것과 유기과산화물 또는 유기과산화물만을 함유한 것으로서 위험
물에 해당하지 아니하는 물품
㉤ 위험물에 해당하지 아니하는 화약류(「총포·도검·화약류 등 단속법」에 의한 화약류에 해당하는 것을 말한다)
㉥ 위험물과 위험물에 해당하지 아니하는 불연성의 물품(저장하는 위험물 및 위험물외의 물품과 위험한 반응을 일으
키지 아니하는 것에 한한다)
② 옥내저장소에 있어서 위험물은 용기에 수납하여 저장하여야 한다. 다만, 덩어리 상태의 황과 제48조의 규정에 의한
위험물에 있어서는 그러하지 아니하다.
③ 옥내저장소에서 동일 품명의 위험물이더라도 자연발화할 우려가 있는 위험물 또는 재해가 현저하게 증대할 우려가
있는 위험물을 다량 저장하는 경우에는 지정수량의 10배 이하마다 구분하여 상호간 0.3m 이상의 간격을 두어 저장하
여야 한다. 다만, 제48조의 규정에 의한 위험물 또는 기계에 의하여 하역하는 구조로 된 용기에 수납한 위험물에 있어
서는 그러하지 아니하다(중요기준).
④ 옥내저장소에서 위험물을 저장하는 경우에는 다음 각목의 규정에 의한 높이를 초과하여 용기를 겹쳐 쌓지 아니하여야
한다.
㉠ 기계에 의하여 하역하는 구조로 된 용기만을 겹쳐 쌓는 경우에 있어서는 6m
㉡ 제4류 위험물 중 제3석유류, 제4석유류 및 동식물유류를 수납하는 용기만을 겹쳐 쌓는 경우에 있어서는 4m
㉢ 그 밖의 경우에 있어서는 3m
⑤ 옥내저장소에서는 용기에 수납하여 저장하는 위험물의 온도가 55℃를 넘지 아니하도록 필요한 조치를 강구하여야
한다.
Ⅱ. 위험물 취급의 기준
1. 위험물의 취급 중 제조에 관한 기준
가. 증류공정에 있어서는 위험물을 취급하는 설비의 내부압력의 변동 등에 의하여 액체 또는 증기가 새지 아니하도록
할 것
나. 추출공정에 있어서는 추출관의 내부압력이 비정상으로 상승하지 아니하도록 할 것
다. 건조공정에 있어서는 위험물의 온도가 부분적으로 상승하지 아니하는 방법으로 가열 또는 건조할 것
라. 분쇄공정에 있어서는 위험물의 분말이 현저하게 부유하고 있거나 위험물의 분말이 현저하게 기계·기구 등에 부착
하고 있는 상태로 그 기계·기구를 취급하지 아니할 것
2. 위험물의 취급중 용기에 옮겨 담는데 대한 기준
가. 위험물을 용기에 옮겨 담는 경우에는 Ⅴ에 정하는 바에 따라 수납할 것
3. 위험물의 취급 중 소비에 관한 기준
가. 분사도장작업은 방화상 유효한 격벽 등으로 구획된 안전한 장소에서 실시할 것
나. 담금질 또는 열처리작업은 위험물이 위험한 온도에 이르지 아니하도록 하여 실시할 것
다. 버너를 사용하는 경우에는 버너의 역화를 방지하고 위험물이 넘치지 아니하도록 할 것
4. 알킬알루미늄등, 아세트알데하이드등 및 다이에틸에터등(다이에틸에터 또는 이를 함유한 것을 말한다) 의 저장기준은
제1호 내지 제20호의 규정에 의하는 외에 다음과 같다(중요기준).
가. 옥외저장탱크 또는 옥내저장탱크 중 압력탱크(최대상용압력이 대기압을 초과하는 탱크를 말한다.)에 있어서는 알킬
알루미늄등의 취출에 의하여 당해 탱크내의 압력이 상용압력 이하로 저하하지 아니하도록, 압력탱크 외의 탱크에
있어서는 알킬알루미늄등의 취출이나 온도의 저하에 의한 공기의 혼입을 방지할 수 있도록 불활성의 기체를 봉입할
것
나. 옥외저장탱크·옥내저장탱크 또는 이동저장탱크에 새롭게 알킬알루미늄등을 주입하는 때에는 미리 당해 탱크안의
공기를 불활성기체와 치환하여 둘 것
다. 이동저장탱크에 알킬알루미늄등을 저장하는 경우에는 20㎪ 이하의 압력으로 불활성의 기체를 봉입하여 둘 것
라. 옥외저장탱크·옥내저장탱크 또는 지하저장탱크 중 압력탱크에 있어서는 아세트알데하이드등의 취출에 의하여 당해
탱크내의 압력이 상용압력 이하로 저하하지 아니하도록, 압력탱크 외의 탱크에 있어서는 아세트알데하이드등의 취출
이나 온도의 저하에 의한 공기의 혼입을 방지할 수 있도록 불활성 기체를 봉입할 것
마. 옥외저장탱크·옥내저장탱크·지하저장탱크 또는 이동저장탱크에 새롭게 아세트알데하이드등을 주입하는 때에는 미리
당해 탱크안의 공기를 불활성 기체와 치환하여 둘 것
바. 이동저장탱크에 아세트알데하이드등을 저장하는 경우에는 항상 불활성의 기체를 봉입하여 둘 것
사. 옥외저장탱크·옥내저장탱크 또는 지하저장탱크 중 압력탱크 외의 탱크에 저장하는 다이에틸에터등 또는 아세트알데
하이드등의 온도는 산화프로필렌과 이를 함유한 것 또는 다이에틸에터등에 있어서는 30℃ 이하로, 아세트알데하이드
또는 이를 함유한 것에 있어서는 15℃ 이하로 각각 유지할 것
아. 옥외저장탱크·옥내저장탱크 또는 지하저장탱크 중 압력탱크에 저장하는 아세트알데하이드등 또는 다이에틸에터등의
온도는 40℃ 이하로 유지할 것
자. 보냉장치가 있는 이동저장탱크에 저장하는 아세트알데하이드등 또는 다이에틸에터등의 온도는 당해 위험물의 비점
이하로 유지할 것
차. 보냉장치가 없는 이동저장탱크에 저장하는 아세트알데하이드등 또는 다이에틸에터등의 온도는 40℃ 이하로 유지할
것
【위험물의 저장온도】