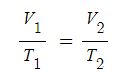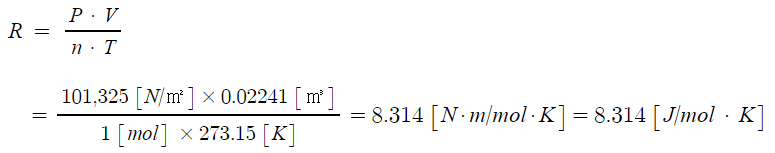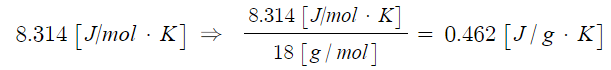아낌없이 주는 나무

​

1. 보일의 법칙

 ▣ 온도가 일정할 때 압력과 부피는 반비례한다.

       PV = K (일정), PV = P'V'

    ※ 풍선을 강하게 누르면 (압력을 증가시키면) 부피는 감소한다.

​

2. 샤를의 법칙

  ▣ 압력이 일정할 때 절대온도와 부피는 비례한다.​

3. 보일-샤를의 법칙

 ▣ 보일의 법칙과 샤를의 법칙을 합친 것​

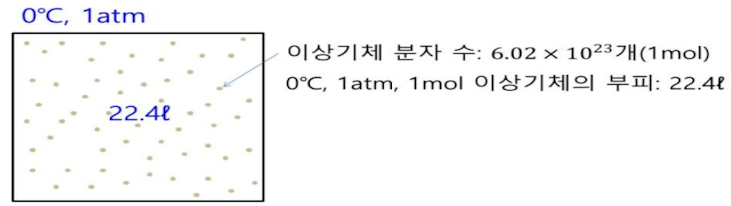
 ▣ 기체 1몰은 0℃, 1기압에서 22.4 ℓ 의 부피를 가지므로 일정한 값을 가진다.​

 ▣ 기체의 몰수에 비례하므로 다음과 같이 이상기체상태방정식이 도출된다.

       PV = nRT

     여기서, P : 압력, V : 부피, n : 기체몰수, R : 기체상수, T : 절대온도

     ※ 이상기체상태방정식이란 이상기체가 압력, 온도 등의 변수에 의해 변하는 상태를 일반적인 식으로 나타낸 것이다.​

     여기서, P : 압력, V : 부피, W : 기체무게, M : 기체분자량, R : 기체상수, T : 절대온도

4. 화학반응 없는 유형

   상태변화 (고체 → 액체 → 기체)만 일어나는 경우이다.​

5. 화학반응이 있는 유형 ★★★

  ▣ 문제에서 질량 등 조건을 제시한 물질과 구해야 하는 물질이 다르므로 몰수 비를 한번 더 곱해준다.

  ※ 밀도를 구하라고 하면​

[개념잡기] 나이트로글리세린 500g이 부피 320 ㎖인 용기 내부에서 분해 폭발 후 압력 (atm)은 얼마인지 구하시오.

                   (단, 폭발온도는 1,000℃ 이며 이상기체로 간주한다.)

 <문제풀이>

  이상기체 상태방정식을 이용한다.

  나이트로글리세린의 분해 화학식은 다음과 같다.

    4C3H5(ONO2)3 → 12CO2 + 10H2O + 6N2 + O2​​

   ⊙ P(압력) = 1atm

   ⊙ M(분자량) = C3H5(ONO2)3 = 12×3+1×5+16×3+14×3+16×2×3=227g/mol

   ⊙ w(질량) = 500g

   ⊙ R (기체상수) = 0.082 atm·ℓ/mol · K

   ⊙ T (절대온도) = 1,000℃ + 273 = 1,273 K​

     1기압에서 1,666.96 ℓ 이므로 0.32 ℓ에서 압력을 구한다.

         PV = P1V1

        1atm × 1,666.96 ℓ = x atm × 0.32ℓ

         x = 5,209.25 atm

​

6. 생성물의 질량 구하기 ★★★

  ▣ 발생하는 물질의 g 또는 ㎏을 구할 때 아래 공식을 사용한다.​​

[개념잡기] 비중이 0.8인 메탄올 10ℓ가 완전연소할 때 소요되는 이론 산소량(㎏)과 생성되는 이산화탄소의 부피 (㎥)를

                  구하시오. (단, 25℃, 1기압)

 <문제풀이>

  ▣ 이상기체 상태방정식을 이용하여 푼다.

     ⊙ 메탄올의 연소식을 먼저 구성한다.

          2CH3OH + 3O2 → 2CO2 + 4H2O​​

   ※ 질량 구하기 - 표준상태 기준​

 ▣ 생성되는 기체의 부피

   ⊙ P(압력) = 1atm

   ⊙ M(분자량) = CH3OH=12+1×3+16+1=32 kg/kmol

   ⊙ w(질량) = 0.8 ㎏/ℓ × 10 ℓ = 8 ㎏

   ⊙ R(기체상수) = 0.082 atm · ㎥ / kmol · K

   ⊙ T(절대온도) = 25 ℃ + 273 = 296 K

#이상기체 #상태방정식 #보일 #샤를 #온도 #압력 #표준대기압 #절대온도 #기체상수

일반 기체 상수 : P V = n R T , 특정 기체 상수 : P V = m R T

​

이상기체 상태방정식에 적용하는 기체상수에는 일반기체 상수 (R)와 특정기체상수(R')가 있다. 이 기체 상수는 모두 기호로 R을 똑 같이 사용하기 때문에 혼동하는 경우가 많다.

이들 기체 상수가 어떻게 구분되는지 알아 보자.

​

기체의 상태를 분석하는데 사용하는 기본 공식으로 이상기체 상태방정식이 있는데 여기에 사용하는 기체상수로 일반기체상수가 적용되느냐, 특정기체상수가 적용되느냐에 따라 이상기체 상태방정식이 다음과 같이 구분된다.

​1. 일반 기체 상수

​

가. 보일의 법칙

보일의 법칙에 따르면 온도가 일정하다면 표준상태 (0℃, 1기압)에서 기체의 부피는 압력에 반비례한다고 한다.

P1 · V1 = P2 · V2

나. 샤를의 법칙

샤를의 법칙에 따르면 압력이 일정하다면 표준상태에서 기체의 부피는 절대 온도와 비례한다고 한다.

그런데 보일의 법칙과 샤를의 법칙은 합하여 하나의 식으로 나타낼 수 있다.​

다. 아보가드로의 법칙

아보가드로는 표준상태 (0℃, 1기압)에서 기체 상태의 물질은 원자량, 분자량 만큼의 질량(g)을 가진 기체의 부피를 1몰 (mol)이라 하는데 모든 기체는 표준상태에서 원자량, 분자량은 달라도 그 부피는 22.4 ℓ 로 동일하고 입자수도 6.02 × 10^23 개로 같다는 것을 알아 냈다.

따라서 아보가드로의 법칙에 따르면 표준상태에서 기체의 부피는 그 기체의 몰수에 의해 결정된다고 한다. 이를 식으로 나타내면 다음과 같다.

그런데 위 비례식을 등식으로 만들기 위해서 사용하는 비례상수가 일반기체상수 (R)이다.

표준 상태에서 1기압 (101,325 [Pa] = 101,325 [N/㎡]), 0 [℃] (273.15 K)인 이상 기체 1 몰(mol)의 부피는 22.41 [ℓ] 이다. 이를 위 식에 대입하여 일반기체상수 (R)을 계산해 보면 8.314 [J/mol · K]이라는 값을 얻을 수 있다.​

기체상수는 기체가 이상기체라고 가정한다면 기체의 종류와 관계없이 일정한 값이 된다.

일반기체상수를 이용하여 이상기체상태방정식을 다음과 같이 표현한다.

P V = n R T

​

2. 특정 기체 상수

​

일반기체상수는 모든 기체에 동일하게 적용되는 비례상수이다. 아보가드로 법칙에 의하면 모든 기체는 표준상태에서 1 몰 (mol)의 부피가 같기 때문에 1 몰 (mol)을 기준으로 모든 기체에 적용할 수 있는 비례상수를 도출하게 되는데 이를 일반기체상수라고 부른다.

​

반면, 특정 기체 상수는 특정한 기체, 개별 기체의 상태방정식에 적용하는 비례상수를 말한다. 개별 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰 질량으로 특정기체상수를 산정한다. 즉, 일반기체 상수는 모든 기체에 적용하기 위해 기체 1몰 (mol)을 기준으로 비례상수를 정하는 반면, 특정 기체 상수는 해당 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰질량으로 나누어 해당 기체 1 [g]을 기준으로 비례상수를 산정한다.

​

예를 들면, '수증기'의 분자식은 H2O이다. 분자량은 18이고 몰질량은 약 18 [g/mol] 이다. (수증기 1몰 (mol)의 무게가 18[g]이라는 뜻이다)

이를 이용하여 일반기체상수 8.314 [J/mol ·K]의 몰 단위 일반기체상수를 몰질량 18 [g/mol] 으로 나누어 주면 수증기의 특정기체상수 0.462 [J/g · K]를 얻을 수 있다.

같은 방법으로 '공기 (몰질량 : 약 29 [g/mol]), 암모니아 (약 17[g/mol]), R-22 (약 86.5 [g/mol]) 등을 이용하여 해당 기체의 특정 기체상수를 구할 수 있다.

위에서 말한 기체의 몰질량과 특정기체상수는 다음과 같다.

일반기체 상수를 Rideal, 특정 기체상수를 Rspecific 라고 하면 이상기체 상태방정식은 다음과 같이 나타낼 수 있다.​

             여기서, M : 몰(mol) 질량, m : 기체의 질량

​

특정기체상수를 이용한 이상기체상태방정식도 일반적으로 PV = mRT 등으로 나타내는데,

이 때 기체상수 R은 특정기체상수임을 주의해야 한다.

​

3. 비열과의 관계

​

어떤 기체가 열을 받으면 이 기체는 온도가 상승함과 동시에 부피가 증가하게 되는데

이 때 '온도 상승'과 '부피의 팽창' 비율은 특정 기체 상수에 따라 정해진다.

어떤 기체가 동일한 '정적 비열'을 가진다고 가정한다면 '특정 기체 상수'가 높으면 이 기체가 열을 받았을 때 외부로 더 많은 일을 하게 된다(온도 변화 대비)고 한다.

특정 기체 상수는 기체의 몰질량이 작을 수록 (다시 말하면 기체가 가벼울 수록) 커지므로

'열을 받은 기체의 몰질량'이 작을 수록 외부로 더 많은 일을 한다(단, 비교하는 기체들이 동일한 정적 비열을 가진다는 가정에서)는 의미가 된다.

        여기서, P · △V : 열을 받은 기체가 외부에 한 일

                     R' : 특정기체 상수, M : 기체의 몰질량

​

#기체상수 #일반기체상수 #특정기체상수 #몰질량 #이상기체 #상태방정식 #비열 #온도

일반 기체 상수 : P V = n R T , 특정 기체 상수 : P V = m R T

​

이상기체 상태방정식에 적용하는 기체상수에는 일반기체 상수 (R)와 특정기체상수(R')가 있다. 이 기체 상수는 모두 기호로 R을 똑 같이 사용하기 때문에 혼동하는 경우가 많다.

이들 기체 상수가 어떻게 구분되는지 알아 보자.

​

기체의 상태를 분석하는 사용하는 기본 공식으로 이상기체 상태방정식이 있는데 여기에 사용하는 기체상수로 일반기체상수가 적용되느냐, 특정기체상수가 적용되느냐에 따라 이상기체 상태방정식이 다음과 같이 구분된다.

​

1. 일반 기체 상수

​

가. 보일의 법칙

보일의 법칙에 따르면 온도가 일정하다면 표준상태 (0℃, 1기압)의 기체의 부피는 압력에 반비례한다고 한다.

P1 · V1 = P2 · V2

나. 샤를의 법칙

샤를의 법칙에 따르면 압력이 일정하다면 표준상태의 기체의 부피는 절대 온도와 비례한다고 한다.

그런데 보일의 법칙과 샤를의 법칙은 합하여 하나의 식으로 나타낼 수 있다.​

다. 아보가드로의 법칙

아보가드로는 표준상태 (0℃, 1기압)에서 기체 상태의 물질은 원자량, 분자량의 만큼의 질량을 가진 기체의 부피를 1몰 (mol)이라 하는데 모든 기체은 표준상태에서 원자량, 분자량은 달라도 그 부피는 22.4 ℓ 로 동일하고 입자수도 6.02 × 10^23 개로 같다는 것을 알아 냈다.

따라서 아보가드로의 법칙에 따르면 표준상태에서 기체의 부피는 그 기체의 몰수에 의해 결정된다고 한다. 이를 식으로 나타내면 다음과 같다.​

그런데 위 비례식을 등식으로 만들기 위해서 사용하는 비례상수가 일반기체상수 (R)이다.​​

표준 상태에서 1기압 (101,325 [Pa] = 101,325 [N/㎡]) 0 [℃] (273.15 K)인 이상 기체 1 몰(mol)의 부피는 22.41 [ℓ] 이다. 이를 위식에 대입하여 일반기체상수 (R)을 계산해 보면 8.314 [J/mol · K]라른 값을 얻을 수 있다.​

기체상수는 기체가 이상기체라고 가정한다면 기체의 종류와 관계없이 일정한 값이 된다.

일반기체상수를 이용하여 이상기체상태방정식을 다음과 같이 표현한다.

P V = n R T

​

2. 특정 기체 상수

​

일반기체상수는 모든 기체에 동일하게 적용되는 비례상수이다. 아보가드로 법칙에 의하면 모든 기체는 표준상태에서 1 몰 (mol)의 부피가 같기 때문에 1 몰 (mol)을 기준으로 모든 기체에 적용할 수 있는 비례상수를 도출하여 이를 일반기체상수라고 부른다.

​

반면, 특정 기체 상수는 특정한 기체, 개별 기체의 상태방정식에 적용하는 비례상수를 말한다. 개별 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰 질량으로 특정기체상수를 산정한다. 즉, 일반기체 상수는 모든 기체에 적용하기 위해 기체 1몰 (mol)을 기준으로 비례상수를 정하는 반면, 특정 기체 상수는 해당 기체에 적용하기 위해 일반 기체 상수를 해당 기체의 몰질량으로 나누어 해당 기체 1 [g]을 기준으로 비례상수를 산정한다.

​

예를 들면, '수증기'의 분자식은 H2O이다. 분자량은 18이고 몰질량은 약 18 [g/mol] 이다. (수증기 1몰 (mol)의 무게가 18[g]이라는 뜻이다)

이를 이용하여 일반기체상수 8.314 [J/mol ·K]의 몰 단위 일반기체상수를 몰질량 18 [g/mol] 으로 나누어 주면 수증기의 특정기체상수 0.462 [J/g · K]를 얻을 수 있다.​

같은 방법으로 '공기 (몰질량 : 약 29 [g/mol]), 암모니아 (약 17[g/mol]), R-22 (약 86.5 [g/mol]) 등을 이용하여 해당 기체의 특정 기체상수를 구할 수 있다.

위에서 말한 기체의 몰질량과 특정기체상수는 다음과 같다.

일반기체 상수를 Rideal, 특정 기체상수를 Rspecific 라고 하면 이상기체 상태방정식은 다음과 같이 나타낼 수 있다.​

여기서, M : 몰(mol) 질량, m : 기체의 질량

​

특정기체상수를 이용한 이상기체상태방정식도 일반적으로 PV = mRT 등으로 나타내는데,

이 때 기체상수 R은 특정기체상수임을 주의해야 한다.

​

3. 비열과의 관계

​

어떤 기체가 열을 받으면 이 기체는 온도가 상승함과 동시에 부피가 증가하게 되는데

이 때 '온도 상승'과 '부피의 팽창' 비율은 특정 기체 상수에 따라 정해진다.

어떤 기체가 동일한 '정적 비열'을 가진다고 가정한다면 '특정 기체 상수'가 높으면 이 기체가 열을 받았을 때 외부로 더 많은 일을 하게 된다(온도 변화 대비)고 한다.

특정 기체 상수는 기체의 몰질량이 작을 수록 (다시 말하면 기체가 가별울 수록) 커지므로

'열을 받은 기체의 몰질량'이 작을 수록 외부로 더 많은 일을 한다(단, 비교하는 기체들이 동일한 정적 비열을 가진다는 가정에서)는 의미가 된다.

여기서, P · △V : 열을 받은 기체가 외부에 한 일

             R' : 특정기체 상수, M : 기체의 몰질량

​

#기체상수 #일반기체상수 #특정기체상수 #몰질량 #이상기체 #상태방정식 #비열 #온도

  ◎ 상태공간법 : 현재의 회로를 바탕으로 미래를 예측하는 것

  ◎ 상태방정식 : 계통방정식이 n차 미분방정식일 때, 이것을 n개의 1차 미분방정식으로

                            바꾸어서 행렬을 이용하여 표현한 것

  ※ 미분방정식 ⇒ 3개의 1차 미분방정식 (행렬) ⇒ 상태천이방정식(상태천이행렬)

     (3차방정식)                        (상태방정식)

                       * 답 찾는 방법 정도만 다룸

​

1. 상태 방정식 

    ※ 시스템행렬과 제어행렬로 나타 내는데 시스템 행렬이 더 중요함

​◎ 상태천이방정식 : 입력 r(t)="0"이고 초기 조건만 주어졌을 때, (초기시간 이후에는

                                 어떤 현상이 나타나는가?) 초기시간 이후에 나타나는 계통의

                                 시간적 변화상태를 나타내는 행렬식

  ※ 상태천이 방정식 안에 상태천이 행렬이 있음

       상태방정식의 일반식

   ※  상태천이행렬의 성질

3. Z변환

 ※ "L" 라플라스변환 : 연속인 선형적 시스템, 규칙적 시스템

    "Z" 변환 : 불연속인 비선형 시스템, 불규칙 이산 시스템

​

① Z변환과 라플라스 변환

③ Z변화의 중요정리​

4. 가제어, 가관측

   : 제어의 기능과 불가능, 관측의 가능과 불가능을 판별한다.