아낌없이 주는 나무

1. 유체가 평판에 부딪혔을 때 작용하는 힘

​

유체의 속도가 변한다는 것은 유체가 힘을 받았기 때문이다.

따라서 유체의 속도가 변하게 되면 역으로 이 때 유체 가해진 힘을 구할 수 있다.

유체의 속도와 힘과의 관계는 다음과 같이 나타낼 수 있다.​

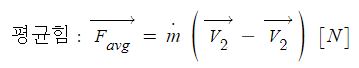
위 식에서 유체의 속도가 변했을 때 가해진 힘은 유체의 질량과 유체의 변화된 속도의 차이의 곱으로 구할 수 있다.

위 그림에서 수평방향으로 V1의 속도로 이동하던 유체가 수직인 벽에 부딪혀 위쪽, 수직 방향으로 1/2 만큼 V2의 속도로 이동하고 아래 쪽 수직방향으로 1/2 만큼 V3의 속도로 떨어지는 경우에 유체에 작용하는 힘을 구해 보자. 이를 구해 보기 위해서는 우선 유체에 작용하는 운동량의 변화를 알아 본다.

먼저 수평 방향 x축 방향의 운동량 변화량은 처음에는 운동량이 mV1이었다가 나중에는 운동량이 "0"이 된다. 수직 방향의 운동량 변화량은 처음에는 운동량이 "0"이었다가 나중에는 1/2 mV2 - 1/2 mV3가 된다. 이는 중력을 이기고 수직방향으로 위쪽으로 1/2 m 만큼 올라가고 나머지 1/2 m 만큼은 아래 쪽으로 떨어졌기 때문이다.

이를 종합하면 유체가 받는 힘은 다음과 같다.​

당초에 수평방향, 오른 쪽 방향으로 향하던 유체가 정지했다는 것은 반대 방향의 힘을 받았다는 것이므로 ( - ) 부호를 붙이게 된다.

Y축 방향, 수직방향으로 작용하는 힘은 벽에 의해 받는 힘이 아니다. 점성이 없다는 가정에서는 말이다. 그렇다면 이 때 유체가 받는 y방향, 수직방향의 힘은 중력에 의해 작용하는 힘이다. 그런데 실제 작용하는 힘은 이와는 다른데 여기서는 가정을 유체가 위로 1/2, 아래로 1/2이 떨어졌다고 가정을 했고 유체의 점성이 없다고 가정을 했기 때문이다.

​

2. 유체가 경사진 평판에 부딪힐 때

​

유체가 경사진 평판에 부딪힐 때 유체가 받는 힘을 구해 보자.

마찬가지로 유체가 받는 힘은 운동량 방정식에 의해 구할 수 있다.​

위 식은 유체의 운동량의 변화는 유체에 작용하는 힘에 의한 것이라는 원리에 따른다.

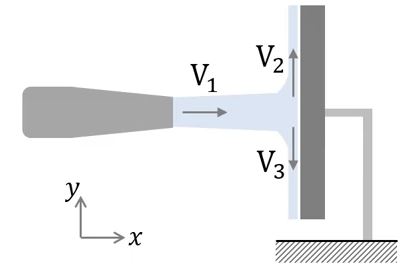
위 그림에서 유체의 수평방향, x축 방향 운동량의 변화는 처음에는 m1·V1이었다가 나중에는 m2V2cosθ - m3V3cosθ 이 되므로 운동량의 변화는 m2V2cos θ - m3V3cos θ - m1V1으로 나타낼 수 있다.

반면 수직방향, y축 방향의 운동량 변화는 처음에는 "0"이었으나 나중에는 m2V2sin θ - m3V3 sin θ 가 되었으므로 운동량의 변화는 m2V2sin θ - m3V3 sin θ 가 된다.

​

3. 유체가 평평한 바닥면에 부딪힐 때

​

평평한 바닥면에 유체가 부딪혔을 때 유체가 받는 힘을 구해 보자.

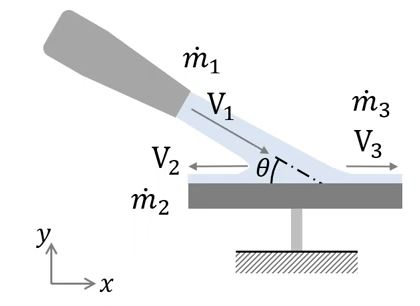
위 그림에서 수평면, x축 방향으로 유체의 운동량 변화량은 당초에는 m1V1 cosθ 였으나 나중에는 m3V3 - m2V2 가 되었으므로 운동량의 변화량은 m3V3 - m2V2 - m1V1 cosθ 가 된다.

또한, 위 그림에서 m1, m2, m3를 구하여 보자.​

m3를 구해 보면​

가 된다.

​

#운동량 #방정식 #유체 #작용하는 #힘 #분류 #충격량 #변화량 #속도

▣ 어떤 용기에 담겨있는 물의 압력이나 고인 물의 압력을 계산하는데는 정수압에 대한 관련식이 필요하다.

물에 의한 압력이 작용하는 사례는 우리 주변에 매우 많다. 위 그림은 미국 콜로라도의 후버댐과 우리나라 소양강댐의

사진이다. 이들 댐을 설계할 때는 정수압의 계산이 필요하다.

즉, 정수력, 유체의 수심에 따라 선형적으로 변동하는 유체의 압력 계산이 필요하다.

그런데 위 그림에서 소양강댐은 댐체가 직선이고 후버댐은 곡선이다. 따라서 수압이 소양강

댐은 평면에 작용하고 후버댐은 곡면에 작용한다. 평면과 곡면에 작용하는 수압을 측정하는 방법에 대하여 알아 보자.

수압의 영향을 받는 구조물은 댐 뿐만 아니라 하천에 설치하는 교각, 가물막이 막, 방파제,

교각설치를 위한 케이슨 등 다양하다.

​

먼저, 평면에 가해지는 정수력에 대해 알아 보자.

대표적인 형태로 소양강댐에 대해 살펴보자. 위 그림의 왼쪽 그림은 소양강댐 전경사진이고

오른쪽 그림은 개념적으로 댐의 단면을 보여주고 있다. 그림에서 댐체의 단면중 공기와 닿

는 부분을 제외한 수중 부분을 보면 댐체와 물을 평면으로 닿고 있음을 알 수 있다.

그런데 평면이냐 곡면이냐에 따라 수압이 댐체에 미치는 영향이 달라진다.

​

정수력은 어떤 면에 수직적으로 작용하는 단위 면적당 힘인데 이 때 입력은 위치에 따라

달라질 수 있기 때문에 수학적으로는 dF/dA에 대하여 극한값을 취하게 된다. 그렇다면

거꾸로 어떤 면에 작용하는 힘은 어떤 면에 작용하는 압력의 미분값을 적분하면 얻을 수

있다. 그런데 어떤 면에 압력이 균일하게 작용한다면 압력 P가 상수가 될 것이다.

이런 경우 작용하는 힘은 압력상수에 면적 곱하여 산정된다.

즉 F = PA로 나타낼 수 있다.

​

앞에서 어떤 면에서 균일하게 압력이 작용한다면 그 면에 작용하는 힘은 압력 × 면적으로

산정할 수 있다고 하였다. 그런데 힘은 벡터이므로 벡터적 관계에서 살펴보자.

위 그림의 왼쪽 그림을 보면 압력이 균일하게 작용한다고 하였으므로 압력 P는 상수가 되고

작용하는 힘은 P × A 가 되는데 힘은 벡터인데 P와 A는 스칼라값이므로 물의 압력에 대응

하는 힘을 산정하려면 압력과 반대방향으로 단위 벡터 n벡터를 추가해야 한다.

오른쪽 아래 그림을 보면 비어있는 십자원은 압력중심이고 유체의 하중을 받는 압력의 중심

을 말한다. 반면 센트로이드는 도심을 의미한다. 위쪽 압력은 균일하므로 압력중심과 도심

의 위치가 같다.

​

이번에는 균일한 압력이 평면이 아닌 곡면에 작용하는 경우를 알아 보자. 위 그림을 보면

비정형인 파란색의 물체가 있다고 하자. 위와같은 물체가 대기중에 있다고 하면 물체의 상

부 쪽 빨간색 화살표 쪽으로 대기압이 작용하게 된다. 물론 위치에 따라 대기압이 다르지만

물체가 크지 않다고 한다면 모든 위치에서 대기압이 같다고 하여도 무방하다. 그러면 이 물

체에 작용하는 힘을 구한다고 한다면 힘은 -nPdA를 적분하면 된다.

그런데 n벡터는 위치에 따라 방향이 바뀌게 되므로 적분할 때 상수로 취급할 수 없게 된다.

따라서 힘을 구하기 위해서는 적분을 해서 구해야 하는데 dA =rdθ 이고 n 벡터는

icosθ + jsinθ 가 된다. 이를 적분을 하면 합이 "0"이 된다.

​

위 그림 왼쪽을 보면 풍선의 내부압력은 풍선이 커지거나 작아지지 않으므로 대기압력과

평행을 이루고 있다고 할 수 있다. 즉 대기압과 같다고 할 수 있으므로 내부 압력은 계기압

력 "0"이 된다. 또한 오른 쪽 그림은 풍선에 작용하는 힘은 풍선에 수직방향으로 균일하게

작용하게 되므로 압력 P에 풍선의 단면적을 곱한 값이 될 것이다. 풍선의 단면적은 πr2이다.

아래 그림에서 물방울의 경우 대기압력과 물방울의 표면장력과 같은 경우와 같은 예라고

할 수 있다.

​

이제 본격적으로 평면에 작용하는 정수력의 크기를 산정하는 방법에 대해 알아 보자.

위 그림의 오른쪽은 소양강댐 사진이고 왼쪽 그림은 댐을 내부에서 바라본 것이라고 가정을

하면 댐체는 수직으로 서 있지 아니하고 경사면을 띠게 된다. 댐체의 면을 Y축이라고 하고

Y축과 수면이 만나는 점을 "O", 수면에서 하늘 쪽 수직방향이 "Z"이라고 하자. 또한 수면과

댐체면이 이루는 각도를 "α"라고 하자.

Y방향으로 작용하는 정수압은 위치에 따라 선형적으로 작용한다는 것을 알 수 있다.

깊이가 깊어지면 압력이 높아진다. 압력을 식으로 나타내면 압력 P = γysinθ라고 할 수 있

다. 여기서 γ 는 물의 단위 중량, 비중량이고 수심은 ysinα 가 된다. 댐체의 어떤 미소면적을

dA라고 하자. 미소면적에 작용하는 힘은 dF =PdA가 된다. 아주 작은 미소면적이므로

압력은 위치에 따라 변하지 않는다고 할 수 있으므로 압력 P'를 상수취급해도 된다.

이 때 P'를 기준으로 하중을 구하자. P'는 도심에 작용하는 압력이다. 작용하는 힘을 구하려

면 적분을 y 즉 도심까지 거리로 적분을 해야 하는데 도심에서의 압력으로 구할 수 있다.

즉, F = P'A로 구할 수 있다.

위 그림의 오른쪽 그림을 보면 노란색 선이 보이는데 이 노란색 단면이 우리가 구하고자 하

는 압력의 단면이다. 미소면적 dA이고 도심까지의 거리가 y, 도심의 압력을 P'라고 하자.

작용하는 힘은 압력 × dA를 적분하면 된다. 그런데 압력 P =γysinα라고 하였으므로

위의 식으로 정리할 수 있다. γsin θ 는 상수이므로 적분식에서 밖으로 나올 수 있으므로

결국 정리하면 F = P'A 가 된다.

​

#압력 #정수압 #벡터 #곡면 #평면 #방정식 #수압 #적분 #미분 #균일압력 #선형적

#소양강댐 #후버댐 #극한값 #상수

1. 충전비 (충전비 체적)

​  ※ 비체적은 #밀도 의 반대개념이다. 즉, 어떤 물질의 단위 질량에 대한 체적의 비를 말한다.

  ⊙ 밀도는 단위 체적당 질량을 말하며 단위로는 [kg / ℓ] 이다.

  ⊙ 반대로 비체적은 단위 질량당 체적을 말하며 단위는 [ℓ/kg]을 쓴다.

  ⊙ 만약 밀도가 1.5 라면 1[ℓ]가 1.5 [kg]이라는 것이고 단위로는 1.5[kg/ℓ]이다.

  ⊙ 비체적이 1.5라며 1[kg]이 1.5[ℓ]라고 것으로 단위로는 1.5[ℓ/kg]을 쓴다.​

  ex) 실(방)의 체적이 270 [㎥] (가로×세로×높이)인 방에 #화재 가 발생하여 #CO2 를

        135[㎥]를 방사했을 때 CO2의 체적 %와 O2의 체적 %는 얼마인가 ?

  ※ 산소체적은 산소의 체적 %가 연소범위 하한인 15 [%] 이하 되었는지 확인하기 위한 것이다. 백분율은 전체 체적에

      대한 해당 물질의 체적의 비를 말한다.

​

  ▣ 이상의 일반적인 체적비를 산출하는 계산식이고 소방에서는 다음의 식으로 산정하다.

  ex) 270[㎥]의 화재실에 CO2를 방사하여 산소농도를 15 [%]로 만들고 싶다면 이산화탄소의 농도와 이산화탄소의 체적은

       얼마인가 ?

[풀이] 먼저 목표로 하는 산소를 농도를 위해 이산화탄소(CO2)의 #체적비 를 구한다.

          구한 이산화탄소(CO2)의 체적비를 이용하여 이산화탄소(CO2)의 체적을 구한다.

​

나. CO2 의 기화체적 [㎥]

  ▣ 일반적으로 물질의 기화체적은 다음식으로 계산한다..

  ▣ 하지만 소방에서는 CO2의 기화체적을 다음 식으로 산정한다.

   ex) 270[㎥] 의 실내의 산소 농도를 15 [%]로 낮출려면 필요한 이산화탄소의 체적은 ?

 ※ 위 식을 이용하면 간단하게 #이산화탄소 (CO2)의 체적을 구할 수 있어 소방에서는

  #이상기체 #방정식 을 사용하지 않고 간략식을 이용하여 계산한다.

【아보가드로의 법칙】

  ▣ 표준상태 (0[℃], 1기압)에서 모든 기체 1 [mol (1kmol)] 이 차지하는 부피는 22.4 [ℓ (㎥)] 이다.

   ⊙ mol → g → ℓ

   ⊙ kmol → ㎏ → ㎥

  ▣ 1 [mol]의 #질량 = #분자량 [g]

  ▣ 1 [kmol]의 질량 = 분자량 [㎏]

​

1. 보일의 법칙 (Boyle's law)

   ※ 보일의 법칙은 온도를 일정하게 한 후에 압력과 부피와의 관계를 나타낸다.​

  ⊙ 이를 그래프로 나타내면 다음과 같다.

2. 샤를의 법칙 (Charl's law)

  ※ 압력이 일정할 때 기체의 #부피 는 온도에 비례한다는 법칙이다.​

    ▣ 샤를의 법칙은 기체의 부피가 기체의 온도에 비례한다는 법칙으로 #프랑스 의 과학자인 샤를 (J. Charles, 1746-

        1823)이 발견하였다.

   ⊙ 이를 그래프로 나타내면 다음과 같다.

3. 보일 - 샤를의 법칙 (Boyle-Charl's law)​

   이를 수식으로 나타내면 다음과 같다. 

4. 이상기체 상태방정식 ★

  ▣ 1834년 프랑스의 물리학자이자 공학자였던 클라페롱(B. P. E. Clapeyron, 1799- 1864)이 보일의 법칙(Boyle's law)과

       #샤를 의 법칙(Charles's law)를 조합하여 고안하였다. 이 방정식은 #동역학적 이론(kinetic theory)를 이용해서도

      유도할 수 있으며, 1856년에 독일 #물리학자 이자 화학자였던 크뢰니히(K. A. Krönig, 1822-1879)와 1857년에 독일

      물리학자이자 #수학자 였던 클라우지우스(R. J. E. Clausius, 1822- 1888)가 서로 독립적으로 발견했다.

   이를 수식으로 표현하면 다음과 같다.

[기체 상수 (R)]​

 < 특정 기체 상태 방정식 >​

【 출제 예상 문제】

​

1. 실내에서 화재가 발생했을 경우, 처음 실내의 온도가 21 [℃]에서 화재시 실내의 온도가 650 [℃]가 되었다면 이로 인하여

     팽창된 공기의 부피는 처음의 약 몇 배가 되는가 ? 

      [단, 대기압은 공기가 유통하여 화재 전이나 후가 거의 같다고 한다.) ①

   ① 3             ② 6                ③ 9                    ④ 12

2. #표준상태 11.2[ℓ]의 기체질량이 22[g] 이었다면 이 기체의 #분자량 은 얼마인가 ? ③

     ① 22              ② 35                   ③ 44                     ④56

3. #위험물 탱크에 압력이 0.3[Mpa]이고, 온도가 0[℃]인 가스가 들어 있을 때 화재로 인하여 100 [℃] 까지 가열되었다면

     압력은 약 몇 [Mpa]인가 ? (단, #이상기체 로 가정 한다) ①

   ① 0.41                ② 0.52                   ③ 0.63                    ④ 0.74​