1. 물질의 특성
가. 물질과 물체
① 물질(物質, Substance)의 고전적 정의는 물체를 이루는 존재를 말하며 공간을 채우고 질량을 갖는 것을 말한다.
즉, 부피와 질량을 함께 가져야 한다. 예) 나무, 쇠, 유리 등
② 물체(物體, object)는 물질로 이루어진 하나의 사물을 의미한다. 물체는 무게와 형태를 갖는다. 예를 들어 하나의 물체
로 다루어지는 야구공은 여러 종류의 물질들로 이루어진 사물이다. 예) 책상, 거울, 축구공, 선풍기 등
나. 물질의 성질 (물리적 성질과 화학적 성질)
① 물리적 성질 : 물질 자체가 갖고 있는 특유한 상태로서 그 물질을 동일한 외적 조건에 두면 항상 동일한 성질을 나타내
며, 시료의 크기나 분할 방법에는 별로 영향을 받지 않는다. 물리적 성질로서의 밀도, 녹는 점, 끓는점,
전도율, 열전도율, 점성도, 결정의 쪼개짐면 등은 높은 정밀도로 측정할 수 있다
※ 물질의 고유 특성은 변화없이 상태만 변할 때 나타나는 성질. 예 : 밀도, 녹는점, 끓는 점, 어는 점, 색 및 용해도 등
㉠ 물질의 상태 변화
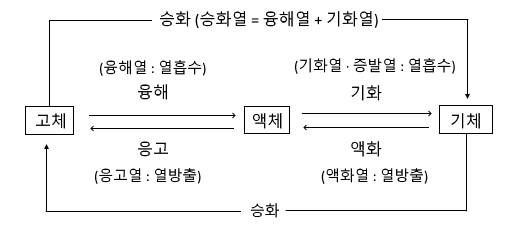
[참고] 물질의 상태와 성질
|
구 분
|
고체
|
액체
|
기체
|
|
성질
|
규칙적 분자배열
|
분자간 인력이 작용
|
분자의 자유로 이동
|
|
형태
|
일정하다
|
용기에 따라 변한다
|
일정하지 않다
|
|
부피
|
일정하다
|
일정하다
|
일정하지 않다
|
|
분자운동
|
일정한 위치에서
진동운동
|
위치가 변하며 느린 진동,
회전, 병진운동
|
고속 진동, 회전, 병진 운동
|
|
분자간 인력
|
강하다
|
조금 강하다
|
극히 약하다
|
|
에너지 상태
|
최소 (안정 상태)
|
보통
|
최대 (무질서한 상태)
|
⊙ 진동운동 : 입자를 구성하는 단위입자 사이의 거리가 늘었다, 줄었다 하는 운동 (고체의 주요 열운동)
⊙ 회전운동 : 입자의 무게 중심을 축으로 회전하는 원운동 (액체의 주요 열운동)
⊙ 병진운동 : 입자가 평행이동할 때와 같은 직선운동. 즉, 평행이동을 하는 운동 (기체의 주요 열운동)
※ 입자 : (粒子, particle, corpuscule)는 물리적 · 화학적 성질을 가진 작은 물체이다. 원자보다 작은 아원자 입자, 원자
몇 개 단위로 구성된 미시적 크기의 미립자, 거시적 크기의 밀가루와 같은 입자 등으로 나뉜다.
물리학에서 입자는 점과 같이 작거나 크기가 없는 역학(mechanics) 운동의 기본 단위를 말한다. 이상적으로는
크기가 없고 질량, 위치와 속도등의 성질만을 갖는다. 때때로 물질의 기본 단위를 일컬으며 이를 기본입자 또는
소립자라고 부르기도 한다.
[참고] 다음에서 일어나는 현상들의 상태변화를 구분하라.
ⓐ 양초의 촛농이 흘러 내리며 굳어 버린다. (응고)
ⓑ 풀잎에 맺힌 이슬이 한낮이 되면 사라진다. (기화)
ⓒ 차창가에 물방울이 맺힌다. (액화)
ⓓ 옷장 속의 좀약의 크기가 조금씩 작아진다. (승화 : 고체 → 기체)
ⓔ 늦가을 맑은 날 아침, 들판에 서리가 내린다. (승화 : 기체 → 고체)
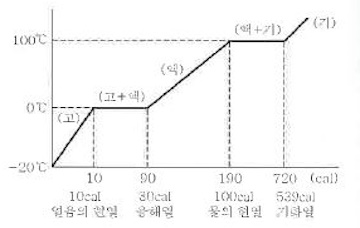
㉡ 물의 상태 변화와 삼상태 ★
ⓐ 물의 현열 : 100 cal/g
ⓑ 얼음의 융해열 (잠열) : 80 cal/g
ⓒ 물의 기화열 (잠열) : 539 cal/g
ⓓ 물의 비열 : 1 cal/g · ℃
ⓔ 얼음의 비열 : 0.5 cal/g · ℃
ⓕ 수증기의 비열 : 0.47 ~ 0.5 cal/g·℃
※ 현열(顕熱)은 물질을 가열이나 냉각했을 때 상변화없이 온도변화에만 사용되는 열량이다.
잠열(潛熱)은 숨은열이란 뜻이다. 어떤 물체가 온도의 변화 없이 상태가 변할 때 방출되거나 흡수되는 열을 말하며 증발
과 응결에 의해 발생하는 열로써 물이 수면이나 습윤한 흙의 표면으로부터 증발할 때 열에너지가 수증기
속으로 들어가는 현상으로 나타난다.
비열용량(比熱容量, Specific heat capacity) 또는 비열은 단위 질량의 물질 온도를 1도 높이는데 드는 열에너지를 말한
다. 비열은 물질의 종류에 따라서 결정되는 상수이며, 밀도, 저항률 등과 같이 물질의 성질을 서술하는 데
중요한 물리량이다.1kg의 물의 온도를 1°C만큼 올리는 데 필요한 열량은 1kcal이므로 물의 비열은 1이 된
다. 그러나 비열은 단순한 숫자가 아니라 단위를 갖는 양이다. 1kg을 1°C 올리는 데 필요한 칼로리수가
비열이므로 비열의 단위는 kcal/kg·°C이다
* 현열 : Q = mC△t, 잠열 : Q = mγ , 비열 : C = Q/m△t
여기서, Q : 열량 (cal), C : 비열 (cal/℃), m : 질량 (g), △t : 온도차 (℃), γ : 잠열 (cal/g)
② 화학적 성질(化學的性質, chemical property) 또는 화학적 특성(化學的 特性)은 어떤 물질의 화학 반응 도중, 또는 화학
반응이 일어난 후에 명백히 드러나는 성질이며, 그 물질 자체가 바뀌지 않는 이상 변하지 않는다. 즉, 화학적
성질은 그 물질을 단순히 보거나 만지는 것만으로는 알 수 없고 는 것이다. 물질의 화학적 성질을 알기 위해서는
그 화학 구조를 살펴보고, 구조에 화학적 변화를 줘봐야 알 수 있다.
예 : 화합, 분해, 치환, 복분해, 반응열, 엔탈피 등
→ 수소와 산소가 반응하여 물을 만들 때 반응 전후의 수소와 산소를 만들 수 없다.
다. 물질의 분류
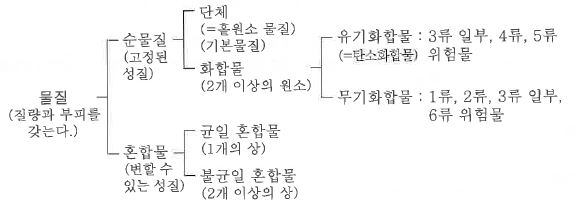
① 순물질 : 조성과 물리적 · 화학적 성질이 일정한 물질을 말한다.
㉠ 단물질 : 한가지 성분으로만 구성된 물질, 더 이상 분해시킬 수 없는 물질
예 : O2 (산소), Cl2 (염소), He (헬륨), Fe (철) 등
㉡ 화합물 : 두가지 이상의 성분으로 구성되어 있으나 성분 원소가 일정한 순물질
예 : H2O (물), CO2 (탄산가스), C6H12O6 (포도당), C2H5OH (알코올) 등
② 혼합물 : 두가지 이상의 순물질이 단순히 섞여 있는 상태를 말한다. 일정한 조성을 갖지 않고 혼합된 순물질 간에 화학
반응으로도 결합되지 않은 상태에 있는 물질을 말한다.
예 : 공기, 음료수, 우유, 시멘트 등
㉠ 균일 혼합물 : 혼합물의 조성이 용액 전체에 걸쳐 동일하다.
예 : 소금물, 설탕물, 사이다
㉡ 불균일 혼합물 : 혼합물의 조성이 용액 전체에 걸쳐 동일하지 않다.
예 : 우유, 찰흙, 화강암, 콘크리트
▣ 순물질과 혼합물의 구별법
⊙ 끓을 때의 순물질과 혼합물의 차이
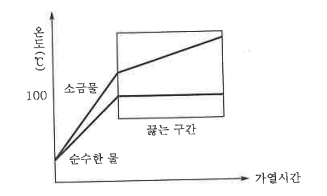
예 : 순수한 물 : 0℃에서 얼고 100℃에서 끓는다. (1기압 상태)
소금물 : 끓는 점은 100℃ 보다 높으며 끓는 동안 소금물은 계속 농축되므로 시간이 흐를수록 끓는 점이 높아진다.
라. 물질 성질의 측정
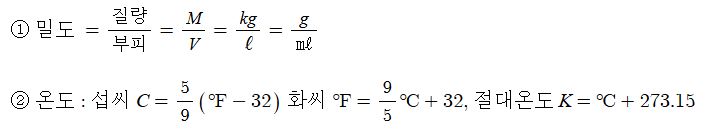
③ 압력 : 1atm = 76㎝Hg =760㎜Hg =14.7psi = 14.7lbf/in2 =1.033227 kgf/㎠
= 101.325 kPa =29.92 inHg = 10.332 mH2O
④ 열량 : Q = mc△T
여기서, Q : 열량 [kcal, cal], m : 질량 [㎏, g], C : 비열 [cal/℃ · g], △T : 온도차 [℃]
2. 원자와 분자
가. 원자의 구조
① 원소와 원자
㉠ 원소(元素, element)는 화학적 방법으로 더 간단한 순물질로 분리할 수 없는 물질이다.
원소는 모든 물질을 구성하는 기본적 요소로, 원자핵내의 양성자 수와 원자번호가 같다.
중성 원자의 양성자의 개수와 전자의 개수는 같다. 현재까지는 118종이 알려져 있다.
㉡ 원자(原子, atom)는 일상적인 물질을 이루는 가장 작은 단위이다. 일상적인 물질들이 원소로
구성되어 있기 때문에, 이는 화학반응을 통해 더 쪼갤 수 없는 단위와 동의어이다.

▣ 원자 : 중심부에 (+) 전기를 띤 원자핵이 있고, 그 주위를 일정한 궤도로 돌고 있는 (-)전기를 띤 전자가 있다.
▣ 원소 : 원자에 붙여진 명칭
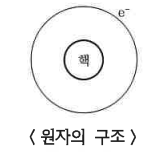
나. 원자핵 (原子核, atomic nucleus)은 원자 중심의 핵자 ( 양성자와 중성자)와 중간자로 이루어진 작고 밀도가 높은 부분
을 말한다. 질량이 거의 같은 양성자와 중성자로 이루어지고, 원자핵 중 양성자와 중성자의 합을 그 원자의 질량수 (원
자량)라 한다.
⊙ 원자번호 = 양성자 수 = 전자 수
⊙ 질량수 = 양성자 수 + 중성자 수
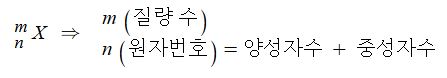
다. 동위원소
▣ 양성자 수는 같으나 중성자수가 다른 원소, 즉, 원자번호는 같으나 질량수가 다른 원소, 또한 동위원소는 양성자 수가
같아서 화학적 성질은 같으나 물리적 성질이 다른 원소이다.

※ 동위원소의 평균 원자량 구하는 법

∴ 동위원소 백분율의 합은 100이 된다.

※ 중수 (산화중수소 (D2O), W=20) : 중수소와 산소의 화합물로서 원자로에서 중성자의 속도를 줄이는 감속제로 사용한다.
라. 동중원소 : 원자번호는 다르나 원자량이 같은 원소, 즉 화학적 성질이 다른 원소이다.
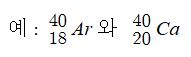
마. 동소체
▣ 같은 원소로 구성되었지만 원자의 배열이 다르거나 같은 화학조성을 가지나 결합양식이 다른 물질
|
구성원소
|
종류
|
연소생성물
|
|
산소 (O)
|
산소 (O2), 오존 (O3)
|
-
|
|
탄소 (C)
|
다이아몬드 (금강석), 흑연, 숯
|
이산화탄소 (CO2)
|
|
인 (P)
|
황린(P4, 노랑인), 적린 (P, 붉은 인)
|
오산화인 (P2O5)
|
|
황 (S)
|
사방황, 단사황, 고무상황
|
이산화황 (SO2)
|
※ 동소체 확인방법 : 연소생성물이 같은지 여부에 따라 동소체를 구별한다.
바. 분자 분자(分子, molecule)
▣ 순물질 (단체, 화합물)의 성질을 띠고 있는 가장 작은 입자로서 1개 또는 그 이상의 원자로 구성되며 원자수에 따라
다음과 같이 구분한다.
① 단원자 분자 : 1개의 원자로 구성 : He (헬륨), Ne(네온), Ar (아르곤) 등 주로 불활성기체
② 이원자 분자 : 2개의 원자로 구성 : H2(수소), O2(산소), CO(일산화탄소), F2(불소), Cl(염소), HCl (염화수소) 등
③ 삼원자 분자 : 3개의 원자로 구성 : H2O (물), O3 (오존), CO2 (이산화탄소) 등
④ 다원자 분자 : 여러개의 원자로 구성 : C6H2O6, C12H23O11 등
⑤ 고분자 : 다수의 원자로 구성 : 녹말, 수지 등
▣ 아보가드로(Avogadro)의 분자설
① 물질을 세분하게 되면 분자가 된다.
② 같은 물질의 분자는 크기, 모양, 질량, 성질이 같다.
③ 분자는 다시 깨져 원자로 된다.
④ 아보가드로의 법칙 : 같은 온도, 같은 압력, 같은 부피 속에서 모든 기체는 같은 수의 기체 분자 수가 존재한다.
사. 이온 (ion)
▣ 전하를 띠는 원자 또는 원자단을 말하며, 전기적으로 중성인 원자가 전자를 잃으면 양전하를, 전자를 얻게 되면 음전
하를 가진 이온이 되며 양이온, 음이온, 라디칼 (radical)이온이 있다.
① 양이온 : 원자가 최외각 전자를 잃어서 (+) 전기를 띤 전하가 된 것.
예) Na 원자 → Na+, e-
(양성자 11, 전자 11) (양성자 11, 전자 10), Ca 원자 → Ca 2+ , 2e-
(양성자 20, 전자 20) (양성장 20, 전자 18)
② 음이온 : 원자가 전자를 얻어서 (-) 전기를 띤 전하가 된 것
예) Cl 원자 + e- → Cl - 이온
(양성자 17, 전자 17) (양성자 17, 전자 18)
O 원자 + 2e- → O2- 이온
(양성자 8, 전자 8) (양성자 8, 전자 10)
③ 라디칼 (radical : 원자단, 기) 이온 : 원자단 (2개 이상의 원자가 결합되어 있는 것)이 전하를 띤 이온(+, -)으로 된 것
예) NH4+(암모니아기), SO42- (황산이온), ClO3-, NO3- (질산이온), MnO4-, CrO42-, CrO72-, BrO3- 등
④ 이온화 경향 : 금속 원자가 최외각전자 (원자가 전자)를 잃고 양이온이 되려는 성질을 말한다.
㉠ 이온화 경향이 큰 금속은 화학적 성질이 강하다.
㉡ 이온화 경향이 수소보다 큰 금속은 산화력이 없는 산에 녹아서 수소를 발생시킨다.
㉢ 이온화 경향이 작은 금속염의 수용액에 이온화 경향이 큰 금속을 담그면, 이온화 경향이 큰 금속은 이온이 되고 작은
금속은 석출된다.
◈ 금속의 이온화 경향 서열에 따른 찬물, 뜨거운 물, 산과의 반응 범위
|
K Ca Na
|
Mg Al Zn Fe
|
Ni Sn Pb
|
(H) Cu Hg Ag Pt An
|
|
찬물과 반응하여
수소 가스 발생
|
끓는 물과 반응하여
수소 가스 발생
|
묽은 산과 반응하여
수소가스 발생
|
반응하지 않음
|
※ --- 친 금속은 양쪽성 원소
3. 화학식량 (원자량, 분자량, 몰)
가. 원자량 (Atomic weight)
▣ 원자량이란 특정 원자의 평균 무게를 통일 원자 질량 단위(unified atomic mass unit; u)에 대한 상대적인 비율로 나타낸
것을 말한다. 상대값이기 때문에 원자량에는 단위가 없다.
① 원자량 : 탄소원자 C의 질량을 12로 정하고 (C의 실제 질량은 1.992 × 10-23 g), 이와 비교한 다른 원자들의 질량비를
원자량이라 한다.
⊙ 탄소 - 12 원자 1개의 질량 = 12 amu
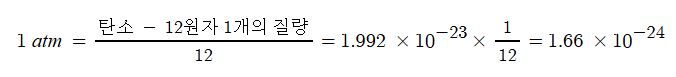
따라서 1 mol을 amu 단위와 관련시키면 다음과 같다.
1 mol = 6.022137 × 1023 amu (아보가드로 수)
ex : 칼슘 (Ca)의 원자량을 40.08로 정한 것은 칼슘이 탄소 - 12 에 비해 (40.08/12) = 3.38 배 무겁다는 것이다.
② g 원자량 : 원자량에 g을 붙여 나타낸 값, 즉, 원자 6.022 × 1023개의 질량을 그 원자의 1g 원자량이라 한다.
ex : 탄소(C) 1g 원자량는 12 g 이다.
※ 아보가드로 수 : 아보가드로는 기체 1 mol (22.4ℓ)에는 모든 기체 분자가 6.022137 × 1023 amu (아보가드로 수) 만큼
존재한다고 했다. 따라서 모든 기체분자 1 mol에는 같은 수 만큼 기체 분자가 존재하므로 각각의 기체
1mol의 질량은 분자량에 g를 붙인 것과 같다. 이를 1g 분자량이라 한다.
③ 원자량을 구하는 방법
㉠ 듀롱페티 (Dulong-petit)의 법칙 (금속의 원자량 측정) : 고체 물질의 원자량 측정에 사용하는 근사적인 실험값이다.
⊙ 원자량 × 비열 ≒ 6.4
㉡ 원자가와 당량으로 원자량을 구하는 방법 : 원자가 × 당량 = 원자량
나. 분자량 ( 分子量, Molecular weight, molecular mass)
① 분자량 분자량(分子量, molecular weight 또는 molecular mass)은 원자 질량 단위로 나타낸 분자의 질량을 말한다.
분자 질량(分子質量)이라고도 하며, 탄소-12를 기준으로 한 상대적 질량이므로 상대 분자 질량이라고도 한다.
: 상대적인 질량을 나타내는 분자량도 원자량 처럼 수치로 표시한다.
※ 분자량 : 각 분자를 구성하는 원소의 원자량을 합한 것이 분자량이다.
⊙ H2 분자량 = 2 (H의 원자량) = 2 × 1 = 2
⊙ H2O 분자량 = 2 (H의 원자량) + (O의 원자량) = 2 × 1+ 16 = 18
⊙ NH3 분자량 = (N의 원자량) + 3 (H의 원자량) = 14 + 3 × 1 = 17
② g 분자량 (mol) : 분자량에 g 단위를 붙여 질량으로 나타낸 값으로서 6.02 × 1023 개의 분자의 질량을 나타낸 값이며
분자 1 mol 의 질량을 말한다.
ex : O2 : 1 mol (1g 분자량) = 32 g, 2 mol (2g 분자량) = 64 g
CO2 : 1 mol (1g 분자량) = 44 g, 2 mol (2g 분자량) = 88 g
다. 몰 (mole)
▣ 물질의 양을 표현하는 단위로 1 몰 (mole)이란 원자, 분자, 이온의 개수가 6.02 × 1023개 (아보가드로수)개 일 때의
부피를 말한다. 기체의 경우 이 양은 22.4ℓ 이고 이는 기체의 종류에 관계없이 일정하다.
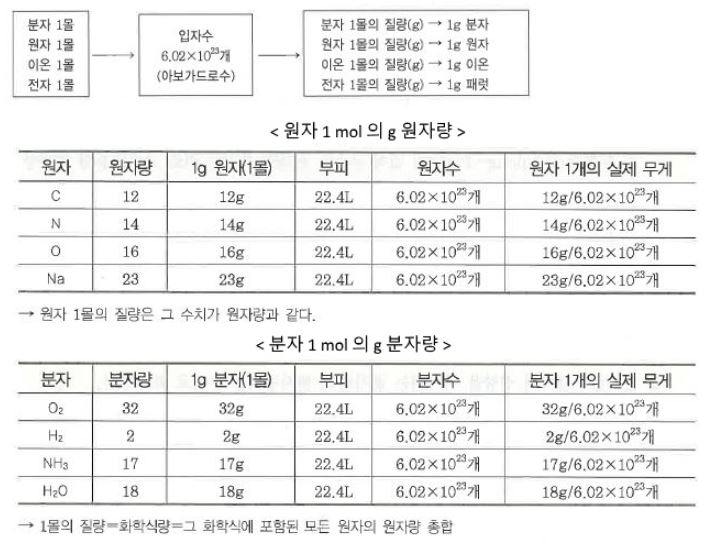
① 1몰의 질량 : 화학식량에 g을 붙인 값으로 원자, 분자, 이온은 6.02 × 1023개의 질량이다.
ex : 탄소(C) 원자 6.02 × 1023 개의 질량은 12 g 이다.
② 물질의 몰수 : 물질의 질량값을 화학식량으로 나눈 값이다.
몰수 = 물질의 질량 / 화학식량
③ 1몰의 부피 : 아보가드로 법칙에 의하여 0℃, 1기압에서 기체 1몰의 부피는 22,4 ℓ 이다.
기체의 몰수 = 표준상태(0℃, 1atm)에서의 기체의 부피(ℓ) / 22.4 ℓ
④ 기체 분자량의 측정 : 0℃, 1atm 에서 1몰(mol)의 기체가 22.4 ℓ 를 차지하므로 0 ℃, 1atm 기체의 부피와 질량을 측정
하여 22.4 ℓ의 질량을 구한다.
기체의 분자량 = 분자 1 ℓ의 질량 × 22.4 ℓ
예제) 공기의 성분이 다음 표와 같을 때 공기의 평균 분자량은 얼마인가 ?
|
성 분
|
분자량
|
부피 함량 (%)
|
|
질소
|
28
|
78
|
|
산소
|
32
|
21
|
|
아르곤
|
40
|
1
|
|
합계
|
?
|
100
|
[문제 풀이]
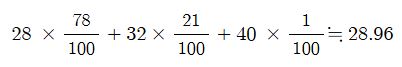
4. 화학식
가. 실험식 (조성식)
▣ 물질의 조성을 각각의 원소의 원자량 분의 질량비율로 간단하게 표현한 식을 말한다.
|
물질
|
분자식
|
조성식
|
|
물
|
H2O
|
H2O
|
|
벤젠
|
C6H6
|
CH
|
|
과산화수소
|
H2O2
|
HO
|
※ 실험식 구하는 방법
화학식 Am, Bn, Cp 라고 하면
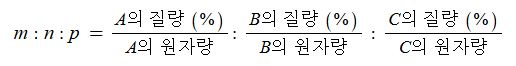
즉, 화합물 성분 원소의 질량 또는 백분률을 알면 그 실험식을 알 수 있으며 실험식에 정수배하면 분자식이 된다.
나. 분자식
▣ 하나의 분자를 구성하는 원소의 종류와 그 원자수를 원소기호와 개수를 표시한 식을 말한다.
조성식 × n = 분자식 (단, n은 정수)
분자량 = 실험식량 × n
ex : 아세틸렌 : (CH) × 2 = C2H2, 물 : H2O, 이산화탄소 : CO2, 황산 : H2SO4
다. 시성식
▣ 분자식 속에 원자단 (라디칼)의 결합상태를 나타낸 화학식으로 유기화합물에서 많이 사용되며 분자식은 같으나 전혀
다른 성질을 갖는 물질을 구분하는데 사용된다.
ex : 아세트산 : CH3COOH (카르복실기 : 산성을 나타내는 작용기)
포름산메틸 : HCOOCH3 , 수산화암모늄 : NH4OH
◈ 원자단 (라디칼, 기)
⊙ 화학변화가 일어날 때 분해되지 않고 한 분자에서 다른 분자로 이동하는 원자의 집단
ex : 포르밀기(-CHO), 카를복실기 (-COOH), 하이드록실기 (-OH), 에테르기 (-O-), 에스터기 (-COO-), 케톤기 (-CO-) 등
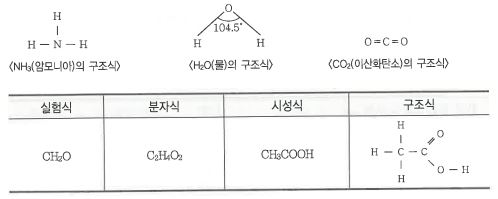
라. 구조식
▣ 화합물에서 원자를 결합선으로 표시하여 원자가와 같은 수의 결합선으로 분자내의 원자들을 연결하여 결합상태를
표시한 식을 말한다.
5. 화학반응의 기본법칙
가. 질량 보존의 법칙
▣ 화학반응에 의해 생성된 물질의 총 질량은 반응전 물질의 총 질량의 합과 같다.
2 H2 + O2 → 2 H2O
2×2g 32g 2 × 18 g
반응전 전체 질량 : 36g = 반응 후 전체 질량 36 g
나. 일정성분비의 법칙
▣ 화합물을 구성하는 성분요소의 질량비는 항상 일정하다.
2 H2 + O2 → 2 H2O
4g 32g 36 g
1 : 8 : 9
예제 : 수소 2g과 산소 21g을 반응시키면 물 몇 g이 생성되겠는가 ? 또 이 중에서 반응하지 않고 남는 것은 무엇이며
몇 g인가 ?
[문제풀이] 2 H2 + O2 → 2 H2O
4g 32g 36 g
1 : 8 : 9
2 g : x g : y g
∴ x = 2g × 8 = 16 g, y = 2g × 9 g = 18 g
[답] 물 18g, 남는 것 O2 : 21 - 16 = 5g
다. 배수비례의 법칙
▣ 한 원소의 일정량과 다른 원소가 반응하여 두 가지 이상의 화합물을 만들 때 다른 원소의 무게비는 간단한 정수비가
성립한다.

라. 기체반응의 법칙
▣ 같은 온도, 같은 압력에서 기체가 서로 반응할 때 반응 전 기체와 반응 후의 기체의 부피 사이에는 간단한 계수비가
나타난다.
2 H2 + O2 → 2 H2O
2부피 : 1부피 : 2부피
예제 : 일정한 온도와 압력에서 수소 15 ㎖ 와 산소 5 ㎖를 반응시키면 몇 ㎖의 수증기가 발생하겠는가 ? 또 남은 것은 무엇
이며 몇 ㎖ 인가 ?
[문제풀이] 2 H2 + O2 → 2 H2O
2부피 : 1부피 : 2부피
10 ㎖ : 5 ㎖ : 10 ㎖
∴ 수증기 10 ㎖ 발생, 수소 15 - 10 = 5 ㎖ 가 남는다.
마. 아보가드로의 법칙 (출제빈도 높음) ★★★
▣ 모든 기체는 같은 온도, 같은 압력, 같은 부피 속에서는 같수 수의 분자가 존재한다.
⊙ 표준상태 (0℃, 1 atm)의 기체 1 mol (22.4ℓ)에는 모든 기체 분자가 6.022137 × 1023 amu (아보가드로 수) 만큼
존재한다.
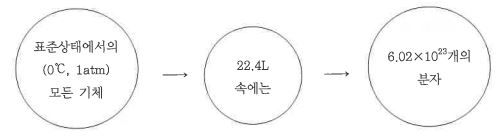
예제 1 : 표준상태에서 질량이 0.8 g 이고 부피가 0.4 ℓ 인 혼합기체의 평균 분자량 (g/mol)은 ?
[문제풀이] 아보가드로의 법칙에 의하면 모든 기체 1mol의 부피는 표준상태에서 22.4 ℓ이므로 다음과 같은 비례식이
성립한다.
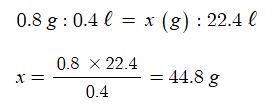
예제 2 : 64g 의 메탄올이 완전연소되면 몇 g의 물이 생성되는가 ?
[문제풀이] 먼저 메탄올의 완전연소시 화학반응식을 세워 보자.
2CH3OH + 3O2 → 2CO2 + 4H2O
1mol 의 CH3OH는 32g 이므로 64g의 메탄올은 2mol이다.
또한 1mol의 H2O는 18g이다. 이제 계수비를 이용하여 생성물의 질량을 알아보자.
2 mol의 CH3OH이 반응하면 4mol의 H2O 생성되고 1mol의 H2O 질량이 18g 이므로
완전연소로 생성되는 물 (H2O)의 질량은 4 × 18 = 72 g 이 된다.
6. 화학반응식과 화학양론
가. 화학반응식
① 화학식 : 화합물을 구성하는 원소들을 간단한 원소기호로 나타낸 것으로 구성 원소의 수와 종류를 나타낸 식을 말한다.
ex : 실험식, 시성식, 분자식, 구조식
② 화학반응식 : 화학반응에 관여하는 물질을 화학식으로 표시하여 반응식으로 나타낸 것으로 반응물 (reactants)과 생성
물 (products)의 관계를 기호로 나타낸 식이다.
※ 화학반응식을 통해 알 수 있는 내용
⊙ 반응물 (반응하는 물질), 생성물 (생성되는 물질)
⊙ 화학반응을 하는 물질들의 화학양론적 관계
⊙ 물질의 상태
㉠ 화학반응식에서는 반응물을 화살표 왼쪽에, 생성물을 화살표 오른쪽에 표기한다.
반응물 + 반응물 → 생성물 + 생성물
㉡ 기본식을 세운다. (반응물과 생성물의 분자식을 표기한다)
프로판 (C3H8)과 산소 (O2)의 반응을 가정하면
C3H8 + O2 → CO2 + H2O
㉢ 양변 각각의 원자수가 같도록 계수를 맞춘다.
a C3H8 + b O2 → c CO2 + d H2O
C : 3a = c
H : 8a = 2d
O : 2b = 2c + d
미지수가 4이고, 식이 3개 이므로 임의의 a를 1로 놓고 계산한다.
∴ a = 1, b = 5, c = 3, d = 4
㉣ 계수를 정수로 맞춘다.
C3H8 + 5 O2 → 3 CO2 + 4 H2O
예제1. C3H8 (g) + 5O2 (g) → 3 CO2 (g) + 4 H2O (ㅣ) 반응식에서 2.3 mol 의 C3H8 이 연소할 때, 다음 물음에 답하시오.
① 필요한 O2 의 몰수를 구하시오.
1 mol : 5 mol = 2.3 mol : x x = 2.3 × 5 = 11.5 mol
② 생성되는 CO2의 몰수를 구하시오.
1 mol : 3 mol = 2.3 mol : x x = 2.3 × 3 = 6.9 mol
예제 2. 다음 반응식을 이용하여 리튬 6.5 mol로 부터 생성되는 산화리튬의 질량을 구하시오.
4 Li (s) + O2 (g) → 2 Li2O (s)
* 리튬(Li) mol 질량 : 6.941 g/mol, Li2O : 13.882+16 = 29.882 g/mol
[문제풀이] 4 : 2 = 6.5 : x 4x = 6.5 × 2 x = 13/4 = 3.25 mol
산화리튬 질량 = 29.882 × 3.25 = 97.1165 ≒ 97.12 g
나. 화학방정식을 이용한 계산
① 반응물질과 생성물질을 확인한다.
② 반응에 관여한 물질의 화학식과 물질의 상태를 쓴다.
③ 화학반응식을 완성한다. (계수를 맞춘다)
④ 분자량과 mol수를 사용하여 mol을 g으로 환산하고 g을 mol로 환산한다.
예제. 프로판(propane) C3H8을 산소 (O2) 중에서 연소하면 다음 식과 같이 이산화탄소 (CO2)와 물 (H2O)이 생성된다.
다음 물음에 답하시오.
C3H8 + 5 O2 → 3 CO2 + 4 H2O
① 22g의 프로판이 연소하면 몇 mol의 이산화탄소가 생성되는가 ?
1 mol의 프로판(C3H8)의 질량 : 12 × 3 + 1× 8 = 44g
1 mol : 3 mol = 0.5 mol : x x = 1.5 mol ∴ 이산화탄소 CO2 1.5 mol
② 22g의 프로판이 연소되면 몇 g의 물이 생성되는가 ?
1 mol : 4 mol = 0.5 mol : x x = 2 mol 물(H2O) 1mol의 질량 : 18 g/mol
물 2 mol 의 질량 = 2 × 18 = 36 g
다. 화학양론 (한계반응물과 이론적 수득량 및 실제 수득량)
① 화학양론 (stoichiometry) : 화합물을 이루는 원소들의 구성비를 수량적 관계로 다루는 이론 (반을물과 생성물 간의
정량적 관계)
㉠ 일정성분비의 법칙 (화합물을 구성하는 각 성분 원소의 질량비는 일정하다)
㉡ 배수비례의 법칙 (2종의 원소가 2종 이상의 화합물을 형성할 때 한쪽 원소의 일정량과 결합하는 다른 쪽 원소의 질량
에는 간단한 정수비가 성립되는 것)
② 과잉반응물 (excess reactant) : 한계반응물과 반응하고 남은 반응물, 즉 이론량 보다 많은 양의 반응물이 첨가된
반응물
③ 한계반응물 (limiting reactant) : 반응을 종료한 후 미반응물이 없는 반응물, 즉 전부 다 반응하는 반응물로 이론량
만큼 첨가된 반응물
④ 화학양론을 이용한 계산
㉠ 반응물질과 생성물질을 확인한다.
㉡ 반응에 관여한 물질의 화학식과 물질의 상태를 쓴다.
㉢ 화학반응식을 완성한다. (계수비를 맞춘다)
㉣ 한계량에 맞추어 구하려는 생성물의 양을 구한다.
㉤ 분자량과 mole 수를 사용하여 mole을 g으로 환산하고 g을 mole 로 환산한다.
[예제] 16.0 g의 CH4 가 48g의 O2와 반응에 의해 생성하는 CO2의 양(g)은 ?
CH4 + 2O2 → CO2 + 2H2O
[문제풀이] 16.0 g의 CH4 = 1 mol CH4 , O2 1mol의 질량 = 32g/mol, 2mol = 64 g
O2 48g = 1.5 mol, O2 1.5 mol과 반응할 수 있는 CH4 mol 수는 ?
1 : 2 = x : 1.5, x = 1.5 / 2 = 0.75 mol
CH4 0.75 mol 반응시 CO2 생성 mol 수는 ? 0.75 mol
CO2 0.75 mol 의 질량은 44 × 0.75 = 33 g
※ 생성되는 CO2의 몰수는 한계반응물인 O2가 결정
1 mol의 CH4 와 반응하는 O2는 2 mol 이며, 1.5 mol의 O2와 반응하는 CH4는 0.75 mol 이다.
따라서 한계반응물은 O2, 과잉반응물은 CH4 이다.
라. 화학방정식으로 부터 이론공기량 구하기
▣ 연소란 열과 빛을 동반한 산화반응이라고 정의되는 것 처럼 연소와 산화라는 단어는 화재화학 영역에서는 어느 정도
동의어적 의미로 사용되고 있다. 일반적으로 메탄의 연소상태를 설명할 때 공기중의 산소와 결합하여 생성물로서
이산화탄소와 물이 생성되는 화학방정식은 다음과 같이 나타낼 수 있다.
CH4 + 2O2 → CO2 + 2 H2O
이와같은 화학방정식에서 1몰의 메탄이 2몰의 산소와 반응하여 1몰의 이산화탄소와 2몰의 물이 생성된다는 것을
알 수 있다. 즉, 이론적으로 요구되는 산소량과 공기량을 구할 수 있는 것이다.
만약, 16g의 메탄이 연소하는데 필요한 이론적 공기량을 구하고자 한다면 다음과 같다.
16 g 메탄은 1mol 이므로 16g의 메탄을 연소시키는데 필요한 O2는 2mol이 필요하다.
공기중에 산소가 21%라고 한다면 2mol의 산소를 얻기 위한 공기량은 2 × 100/21 = 9.52 mol이 된다.
공기의 1mol의 질량은 28.84 이므로 9.52 mol의 질량은 28.84 × 8.52 = 274.56 g이다.
이와 같은 방법으로 아보가드로의 법칙에 의해 각각의 생성되는 CO2 및 H2O의 양도 g, ℓ, 분자 수의 개수 등의 단위
로 얼마든지 환산하여 낼 수 있다.
◈ 16g의 메탄이 연소하는데 필요한 이론적 O2의 양(ℓ)은 ?
CH4 + 2O2 → CO2 + 2 H2O
메탄 16g 즉, 1 mol의 메탄을 완전 연소시키는데 필요한 산소는 2 mol 이고 산소 1 mo은 22.4 ℓ 이므로 O2 2 mol은
44.8 ℓ 이다.
◈ 16g의 메탄이 연소하는데 필요한 이론적 O2의 분자개수는 ?
CH4 + 2O2 → CO2 + 2 H2O
메탄 16g 즉, 1 mol의 메탄을 완전 연소시키는데 필요한 산소는 2 mol 이고 산소 1 mol 부피속 에는 산소 분자가
6.02 × 1023 개 들어 있므로 O2 2 mol 속에는 6.02 × 1023 × 2 = 12.04 × 1023 개의 O2의 분자가 들어 있다.
◈ 16g의 메탄이 연소하면 생성되는 CO2의 분자개수는 ?
CH4 + 2O2 → CO2 + 2 H2O
메탄 16g 즉, 1 mol의 메탄을 완전 연소하면 CO2는 1 mol 이 생성되고 CO2 1 mol 부피속 에는 이산화탄소 분자가
6.02 × 1023 개 들어 있다.
◈ 16g의 메탄이 연소하면 생성되는 물(H2O)의 분자개수는 ?
CH4 + 2O2 → CO2 + 2 H2O
메탄 16g 즉, 1 mol의 메탄을 완전 연소하면 H2O는 2 mol 이 생성되고
H2O 1 mol 부피속 에는 이산화탄소 분자가 6.02 × 1023 개 들어 있다.
H2O 2 mol 속에는 6.02 × 1023 × 2 = 12.04 × 1023 개의 H2O 분자가 들어 있다.
[예제] CH4 + 2O2 → CO2 + 2H2O 인 메탄의 연소반응에서 메탄 1 ℓ 에 대해 필요한 공기 요구량은 약 몇 ℓ인가 ? (단, 0℃,
1atm이고, 공기 중의 산소는 21%로 계산한다.)
CH4 + 2O2 → CO2 + 2H2O
[문제풀이] 메탄 (CH4) 1몰을 완전연소하는 완전연소하는데 산소(O2) 2 mol이 필요하고 공기중에는 산소(O2)가 21 %
존재하므로 메탄 (CH4) 1 mol을 완전연소하는데 요구되는 공기량은 2 mol × 100 / 21 이다.
∴ 메탄 (CH4) 1 ℓ를 완전연소하는데 요구되는 공기량은
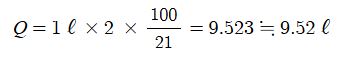
#화학양론 #아보가드로 #질량보존법칙 #화학방정식 #한계반응물 #과잉반응물 #일정성분비
'위험물 기능장 > 일반화학및유체역학' 카테고리의 다른 글
| 산화 · 환원 반응 (화학반응) (6) | 2024.11.17 |
|---|---|
| 용액과 용해도 (0) | 2024.11.13 |
| 산과 염기 (2) | 2024.11.12 |
| 물질의 화학결합 (0) | 2024.11.09 |
| 원자의 구조와 원소의 주기율 (8) | 2024.11.07 |
