1. 용액
가. 용액
▣ 용액(溶液, solution)은 둘 이상의 물질로 구성된 혼합물의 일종으로, (액체상태뿐만 아닌, 물질의 상태에 관계없이
두가지 이상의 물질이 고르게 섞여있는 것은 모두 용액 이라고 한다.) 액체나 기체 등의 물질에 다른 물질이 섞여 들어
가 그 조성이 위치에 상관없이 균질하게 된 것을 말한다. 이때 용액의 대부분을 이루는, 용액의 매체가 되는 물질을 용
매라고 하며, 용매에 섞여 들어가는 물질을 용질이라고 한다. 특히, 용매가 물인 경우의 용액을 수용액이라 한다.
물 + 소금 ⇒ 소금물
(용매) (용질) (용액 )
나. 극성 용매와 비극성 용매
▣ 극성 분자는 극성 용매에, 비극성 분자는 비극성 용매에 녹는다.
ex : 알코올은 물에 잘 녹는다. (알코올과 물은 극성이다)
가솔린은 물에 녹지 않는다. (가솔린은 무극성, 물은 극성이다)

다. 용액의 분류
|
구 분
|
농 도
|
비 고
|
|
불포화 용액
|
용질이 더 녹을 수 있는 상태의 용액
|
석출속도 < 용해 속도
|
|
포화 용액
|
일정한 온도, 압력하에서 일정량의
용매에 용질이 최대한 녹아 있는 용액
|
더 이상 녹일 수 없으며 더 이상 넣으면 고체로
가라 앉는다. (석출속도 = 용해속도)
|
|
과포화 용액
|
용질이 한도 이상으로 녹아 있는 상태의 용액
|
용질을 더 넣어도 녹지 않고 외부의 충격에 의해
포화상태 이상으로 녹은 용질이 석출된다.
(석출속도 > 용해속도)
|
다. 용해도 곡선
▣ 온도 변화에 따른 용해도의 변화의 관계를 나타내는 그래프

2. 용해도
가. 고체의 용해도
▣ 용매 100g 에 용해되는 용질의 최대 g 수, 즉 포화용액에서 용매 100g에 용해된 용질의 g 수를 그 온도에서 용해도라
한다.
ex : 물 100 g 에 소금은 20 ℃에서 35.9 g 녹으면 포화된다. 따라서 20℃ 일 때 소금의 물에 대한 용해도는 35.9 이다.

예제) 20℃의 물 500g에는 설탕이 몇 g까지 녹을 수 있는가 ? (단, 20℃ 의 물에 대한 설탕의 용해도는 204 이다.)
[풀이] 20 ℃의 물 100g에 설탕은 204g 까지 녹을 수 있다. 따라서 500g 에 녹을 수 있는 설탕 x (g)은 ?
100 : 204 = 500 : x, x = 204 × 500 / 100 = 1,020 g
나. 기체의 용해도
① 온도의 영향 : 기체가 용해되는 과정은 발열반응이므로 온도가 높을 수록 기체의 용해도는 감소한다.
② 압력의 영향 (헨리의 법칙)
㉠ 용액에서 기체의 용해도는 그 기체의 압력에 비례한다.
㉡ 기체의 용해도는 여러 종류의 기체가 혼합되어 있을 경우 그 기체의 부분 압력과 몰분율에 비례한다.
㉢ 일정한 온도에서 용매에 녹는 기체의 질량은 압력에 비례하나, 압력이 증가하면 밀도가 커지므로 녹는
기체의 부피는 일정하다.
* 녹는 기체의 질량 w = kP (T 일정)
<참고> 헨리의 법칙은 용해도가 작은 기체이거나 무극성 분자일 때 잘 적용된다. 차가운 탄산음료수의 병마개를 뽑으면
거품이 솟아 오르는데, 이는 탄산 음료수에 탄산가스가 압축되어 있다가 병마개를 뽑으면 압축된 탄산가스가
분출되어 용기의 내부압력이 내려가면서 용해도가 줄어 들기 때문이다.
ex : H2, O2, N2, CO2 등 무극성 분자
③ 재결정 : 온도에 따른 용해도 차가 큰 물질에 불순물이 섞여 있을 때 고온에서 물질을 용해시킨 후 냉각시켜 용해도
차이로 결정을 석출하는 방법
다. 수화물
▣ 결정수를 가진 결정을 가열하여 결정수를 일부 또는 전부 제거하면, 일반적으로 결정이 파괴되어 다른 결정형으로
되거나 분말 (가루)로 된다.
ex : CuSO4 · 5H2O (s) (청색) →(가열) ← (수분 흡수) CuSO4(s) (백색분말) + 5 H2O (g)
이 반응은 가역반응이며, 색깔의 변화를 이용하여 수분의 검출에 이용된다.
① 풍해 (風解) : 결정수를 가진 결정, 즉 수화물이 스스로 공기 중에서 결정수의 일부나 전부를 잃어 분말로 되는 현상을
풍해라 한다.

② 조해 (潮海) : 고체 결정이 공기 중의 수분을 흡수하여 스스로 용해하는 현상을 조해라 한다.
일반적으로 조해성을 가진 물질은 물에 대한 용해도가 크다.
1류 위험물 (산화성 고체)은 조해성 물질이다.
ex : NaOH(s) · KOH · CaCl2 · P2O5 · MgCl2
(건조제로 이용)
3. 용액의 농도
가. 몰분율 (XA)
▣ 혼합물 속에 한 성분의 몰수를 모든 성분의 몰수로 나눈 값

나. 퍼센트 농도 (%)
▣ 용액에 대한 용질의 질량 백분율
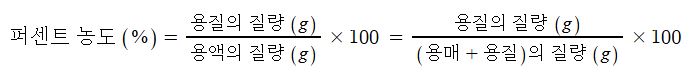
다. 몰농도 (M)
▣ 용액 1ℓ (1,000㎖)에 포함된 용질의 몰 수

여기서, g : 용질의 g 수, M : 분자량, V : 용액의 부피 (㎖)
라. 몰랄 농도
▣ 용매 1,000g에 녹아 있는 용질의 몰 수 (m)인 몰랄 농도는 질량 (㎏)을 사용하기 때문에 온도가 변하는 조건에서
이 몰랄농도를 사용한다.

마. 노르말 농도
▣ 용액 1ℓ (1,000㎖) 속에 녹아 있는 용질의 g당량수를 나타낸 농도

<참고> 당량
◈ 전자 1개와 반응하는 양을 당량이라고 하는데 정확히 수소 1g 또는 산소 8 g과 반응할 수 있는 그 물질의 양을 1g 당량
이라 정의 한다.

바. 농도의 확산
① 중량 %를 몰농도로 환산하는 법 : 중량 %를 몰농도로 환산할 때에는 다음과 같이 용액 1ℓ에 대하여 계산한다.
◈ 중량 백분율 a (%) 용액의 몰농도 x를 구해 보자.
이 용액의 비중을 S, 용질의 질량 w (g)은 얼마인가 ?

◈ 용질 w(g)의 몰수는 용질의 분자량(식량) M으로 부터 w/M이 된다.
따라서, 몰 농도는 다음과 같이 구할 수 있다.

② 몰 농도를 중량 %로 환산하는 법 : 몰농도를 중량 %로 환산할 때도 용액 1ℓ의 질량과 이 속에 녹아 있는 용질의 질량을
구하여야 한다.
◈ n 몰 농도 용액의 중량 백분율 x (%)를 구해 보자.
이 용액의 비중을 S, 용질의 분자량을 M이라 하면 이 용액 1ℓ의 질량 w (g)은 얼마인가 ?
w = 1,000 × S (g)
이 용액 1ℓ 속의 용질의 질량 m (g) 은 ? m = n · M (g)
중량 백분율 x (%)는 용액의 질량 100 g 에 대한 g 수 이므로
1,000 × S : nM = 100 : x

사. 혼합용액의 농도
MV ± M'V' = M" (V+V') (액성이 같으면 +, 액성이 다르면 -)
MV ± N'V' = N" (V+V')
아. 끓는 점 오름과 어는 점 내림

▣ 용액은 순수한 용매보다 증기압이 낮아지므로 용액의 끓는 점은 순수 용매의 끓는 점 보다 높아지고
용액의 어는 점은 순수한 용매 보다 낮아진다. 이는 몰랄 농도에 비례하여 변한다.
|
구 분
|
끓는 점
|
어는 점
|
|
순수한 용매
|
낮음
|
높음
|
|
용액
|
높음
|
작음
|
① 끓는 점 오름
㉠ 용액의 끓는 점은 용매의 끓는 점 보다 높다.
㉡ 끓는 점 오름 (△Tb)은 용액의 몰랄농도 (m)에 비례한다.
△Tb = kb m (kb : 몰랄 오름 상수)
② 어는 점 내림
㉠ 용액의 어는 점은 용매의 어는 점 보다 낮다.
㉡ 어는 점 내림 (△Tf)은 용액의 몰랄농도 (m)에 비례한다.
△Tf = kf m (kf : 몰랄 내림 상수)
③ 전해질 용액의 끓는 점 오름과 어느 점 내림 : 1분자가 2개의 이온으로 전리하는 전해질 용액의 전리도를 α 라 하면,
전해질 1 mol은 비전해질 (1+α) mol에 해당한다. 따라서, 전해질 용액은 같은 몰 수의 비전해질 몰 수 보다 (1+α)배
끓는 점이 높고 어느 점이 낮다.
④ 삼투압 : 용액중 작은 분자의 용매는 통과시키나 분자가 큰 용질은 통과 시키지 않는 막을 반투막이라 한다.
ex : 동식물의 원형질막, 방광막, 콜로디온막, 셀로판 황산지 등은 불완전 반투막이다.

▣ 반투막을 경계로 동일 용매에 다른 용액을 접촉시키면 양쪽의 농도가 같게 되려고 묽은 쪽 용매가 반투막을 통하여
농도가 진한 용매 쪽으로 침투한다. 이때 반투막에 작용하는 압력을 삼투압이라 한다.
<참고> 비전해질의 묽은 수용액의 삼투압은 용액의 농도 (몰농도)와 절대온도 (T)에 비례하며, 용매나 용질의 종류와는
관련이 없다.
⑤ 반트 호프의 법칙 : 일정한 부피 속에 여러가지 비전해질 용질 1 몰 씩을 녹인 용액의 삼투압은 모두 같다.
이를 반트 호프의 법칙이라 한다.

어느 V(ℓ)의 묽은 용액 속에 어떤 용질 n 몰이 녹아 있을 때 농도는 n/V (몰/ℓ)가 될 것이며,
이 때 절대 온도를 T라 하면, 이 용액의 삼투압 π는 다음과 같은 식으로 나타낼 수 있다.

실험에 의하면 k는 이상 기체 상수 R과 같다. 따라서 위 식은 이상기체 상태방정식과 같은 관계식으로
아래와 같이 나타낼 수 있으며 V(ℓ) 속에 분자량이 M인 용질 w(g)가 포함되어 있다면 이 용질의 몰 수는
n = w/M 이므로 이를 기체 상태 방정식에 대입할 수 있다.

<참고> 삼투압은 πV = nRT 의 단위에 주의하여야 한다. π 는 삼투압 (Pa, kPa), V는 부피 (ℓ, ㎥), n은 몰 수, T는 절대온도
(273.15 + ℃), R = 0.0821 (1 atm · ℓ / mol · K)이다.
4. 콜로이드 용액
가. 콜로이드 입자
▣ 전분, 단백질 등은 분자량이 크고, 분자의 크기가 10 ~ 100 A 의 범위에 있으며 결정이 잘 되지 않는다.
이러한 크기의 입자를 콜로이드 입자라 한다.
나. 콜로이드 용액의 성질
① 틴들현상 : 콜로이드 용액에 강한 빛을 통하면 콜로이드 입자가 빛을 산란하게 하기 때문에 빛의 통로가 보이는 현상을
말한다.

※ 한외 현미경 : 틴들현상을 이용하여 콜로이드 입자의 수와 운동상태를 볼 수 있는 현미경
예 : ⊙ 어두운 곳에서 손전등으로 빛을 비추면 먼지가 보인다.
⊙ 흐린 밤중에서 자동차 불빛의 진로가 보인다.
② 브라운 운동 : 콜로이드 입자들이 불규칙하게 움직이는 것

③ 투석 : 콜로이드 입자는 거름 종이를 통과하거나 반투막 (셀로판지, 황산지, 원형질막)은 통과하지 못하므로 반투막을
이용하여 보통 분자나 이온과 콜로이드를 분리, 정제하는 것 (콜로이드 정제에 이용)이다. 이와 같은 성질을
이용한 것이 투석이다.

<참고> 콜로이드 입자는 투석막을 통과하지 못한다.
셀로판지와 투석막은 보통의 이온이나 분자 등은 통과시키나, 콜로이드 입자는 통과시키지 못한다.
④ 전기 영동 : 전기를 통하면 콜로이드 입자가 어느 한 쪽 극으로 이동한다.
예 : 집진기를 통한 매연 제거

◈ 콜로이드 입자는 전기를 띠고 있어 (+) 콜로이드는 (-)극으로, (-) 콜로이드 입자는 (+)극으로 이동한다.
⑤ 엉김과 염석 : 콜로이드가 전해질에 의해 침전되는 현상이다. 이 현상은 몰 수와 관계없이 전해질의 전하량이 클 수록
효과적이다.
예 : (+) 콜로이드일 경우 → 음이온 : 비고 PO43- > SO42- > Cl-
(-) 콜로이드일 경우 → 양이온 : 비고 Al3+ > Mg2+ > Na+
㉠ 엉김 : 소수 콜로이드가 소량의 전해질에 의해 침전
ex : 흙탕물에 백반 (전해질)을 넣어 물을 정제한다.
※ 소수 콜로이드 : 물과 친하지 않아 소량의 물분자로 둘러 쌓여 있는 콜로이드 : Fe(OH)2, Al(OH)3
㉡ 염석 : 친수 콜로이드가 다량의 전해질에 의해 침전
ex : MgCl2를 넣어 두부를 만든다.
(전해질)
※ 친수 콜로이드 : 물과 친하여 다량의 물분자로 둘러 쌓여 있는 콜로이드 : 전분, 젤라틴, 한천 등
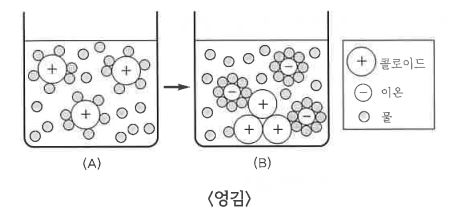
(A) : 입자들이 같은 극성의 전하를 띠고 있기 때문에 서로 반발하여 안정된 상태를 유지한다.
(B) : 서로 다른 극성의 이온이 첨가 되어 용질이 전하를 잃고 콜로이드가 엉긴다.
#전해질 #콜로이드 #이온 #엉김 #투석 #삼투압 #반트호프 #농도 #용액 #용해도 #용매 #용질
'위험물 기능장 > 일반화학및유체역학' 카테고리의 다른 글
| 무기화합물 (0) | 2024.11.18 |
|---|---|
| 산화 · 환원 반응 (화학반응) (6) | 2024.11.17 |
| 산과 염기 (2) | 2024.11.12 |
| 물질의 화학결합 (0) | 2024.11.09 |
| 원자의 구조와 원소의 주기율 (8) | 2024.11.07 |
