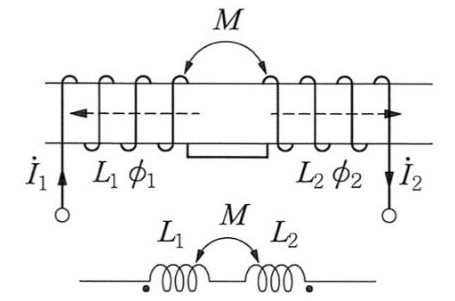
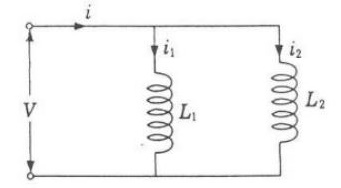
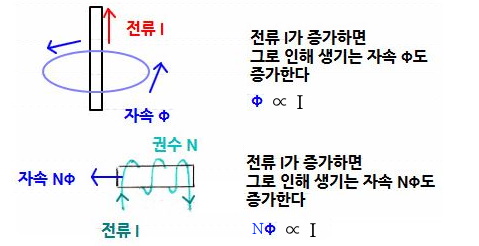
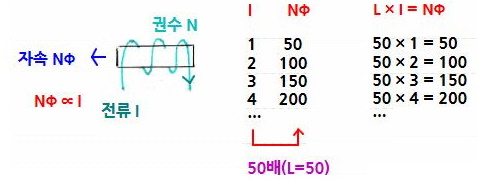
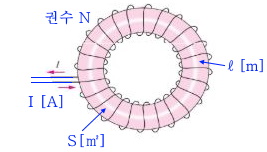
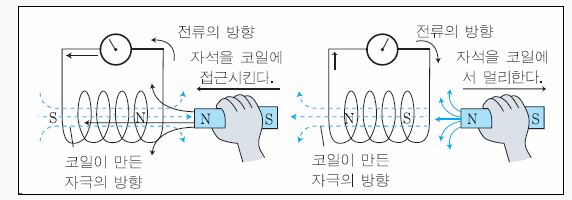
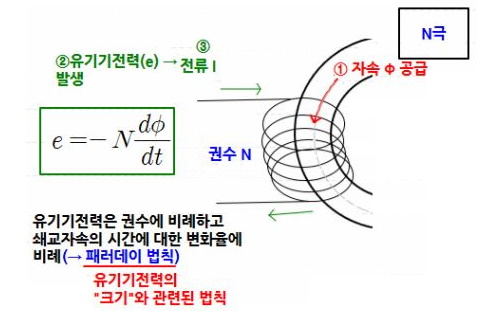
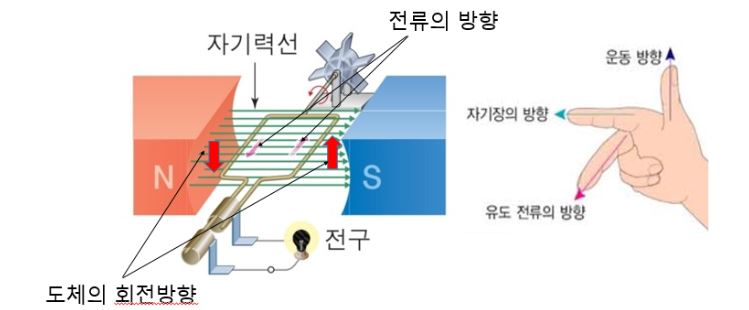
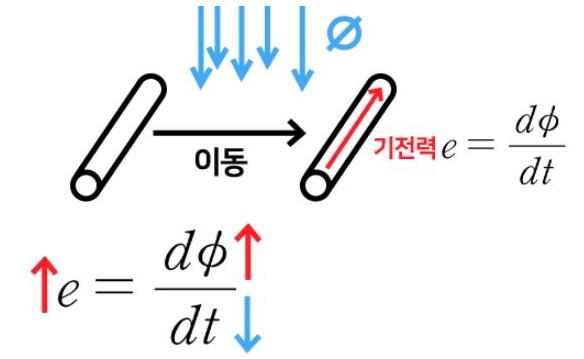
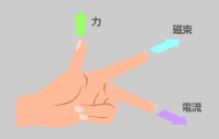
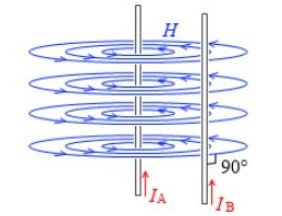
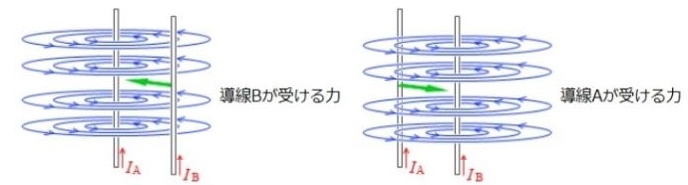
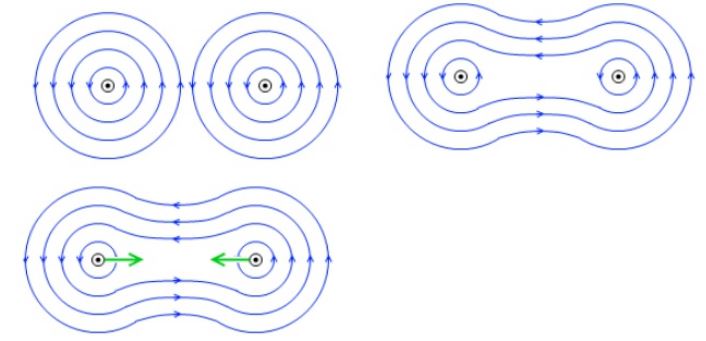
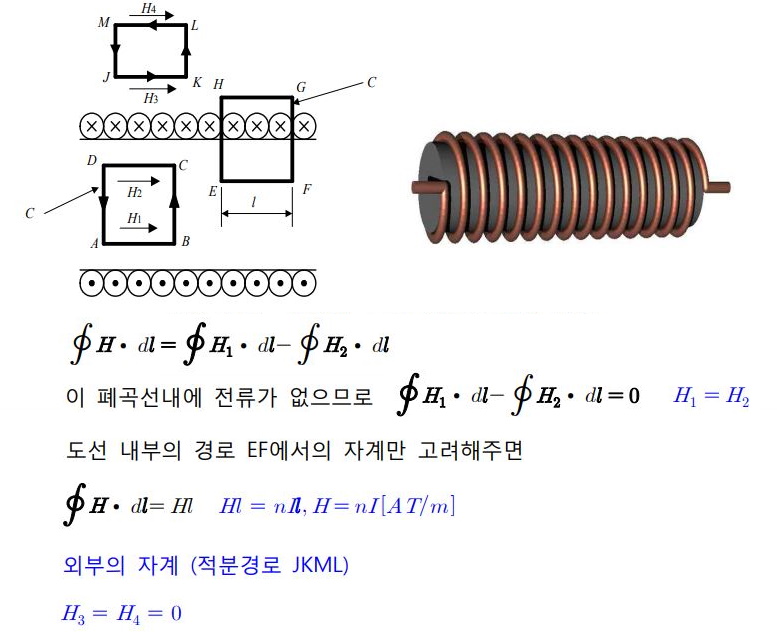
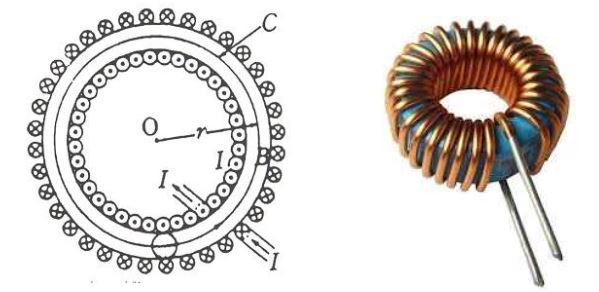
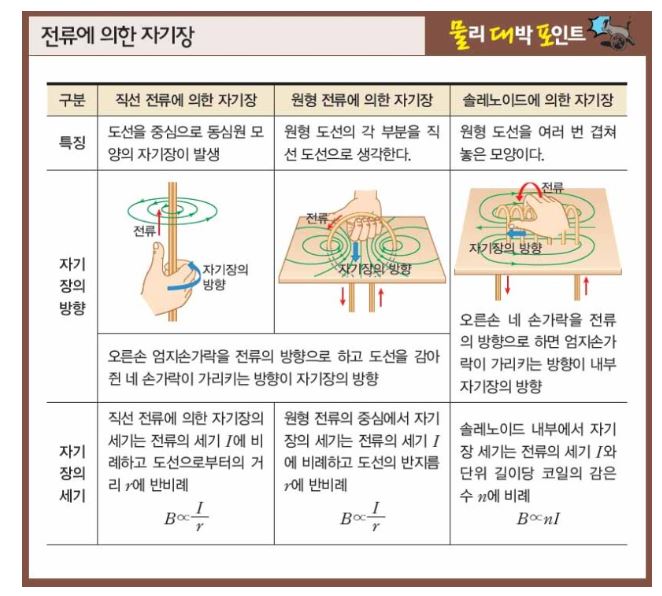
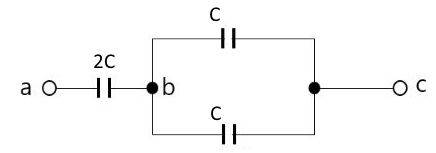
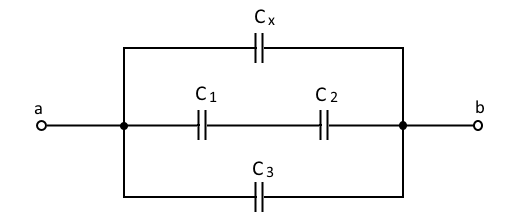
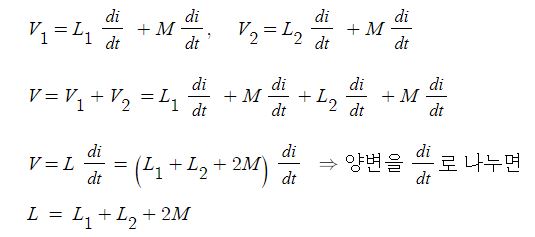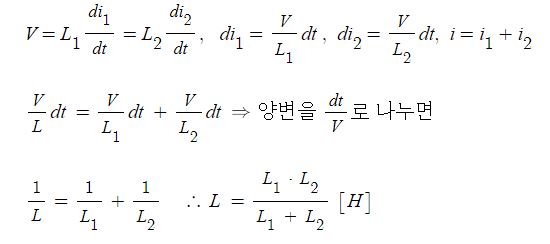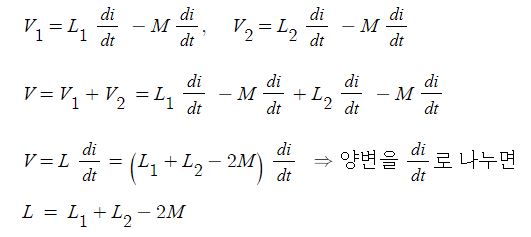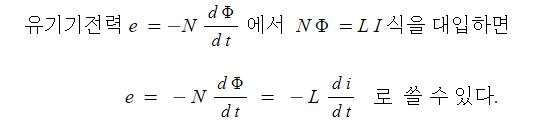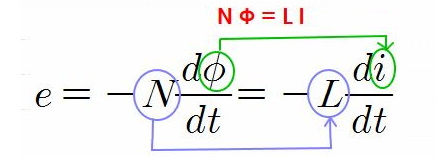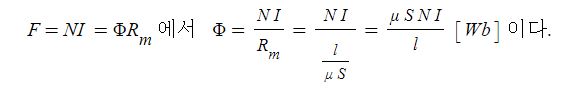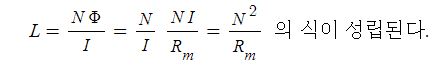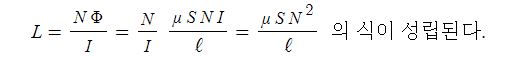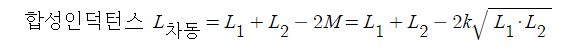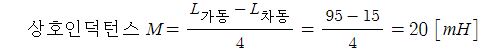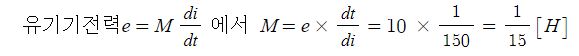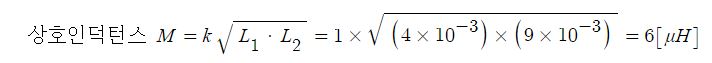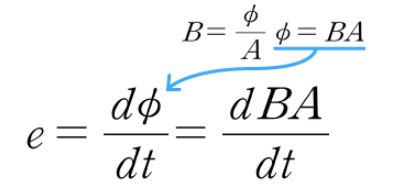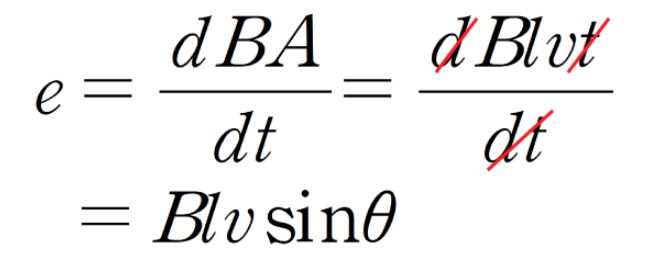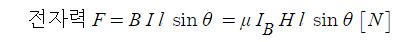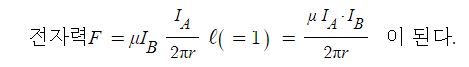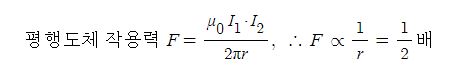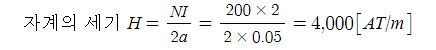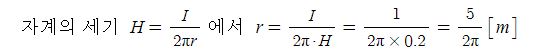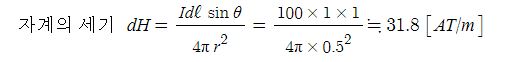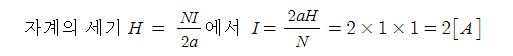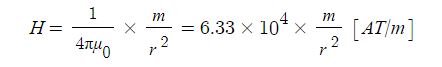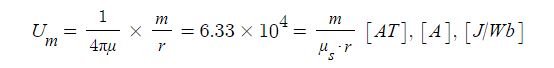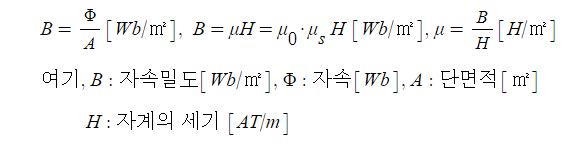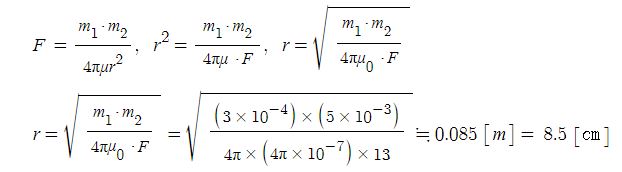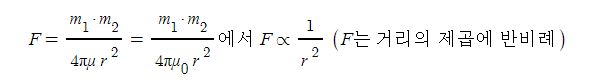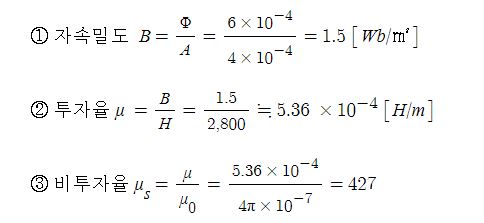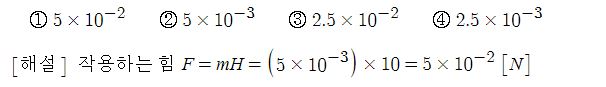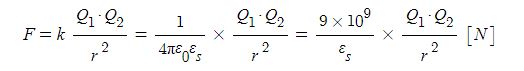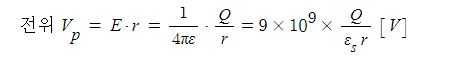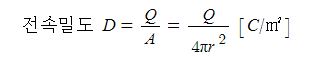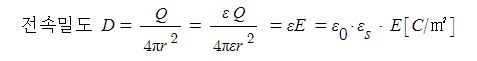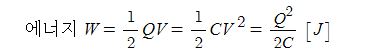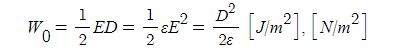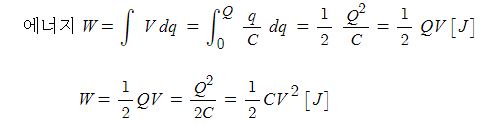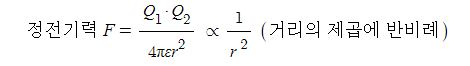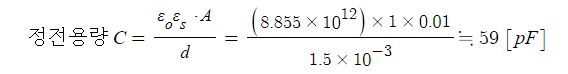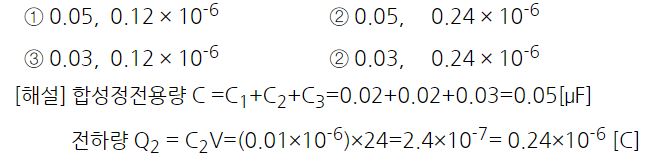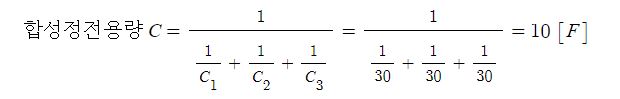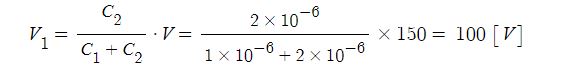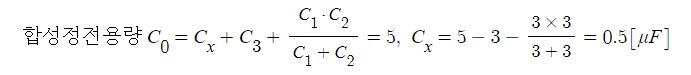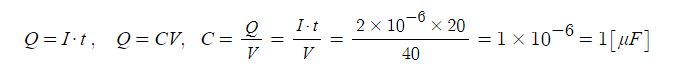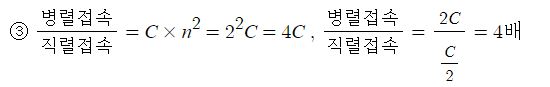1. 자기장
가. #자석
▣ 철광(주성분 FeO)은 철이나 니켈 등을 끌어들이는 성질을 가지고 있는데, 이러한 성질을 자성이라 하며,
이 작용을 자기(mag-netism)라고 한다. 자성을 가진 물체를 자석 (magnet)이라 하고, 자석의 양 끝을
자극(magnetic pole)이라고 한다. 자석에는 N극과 S극이 있는데, 이들이 단독으로는 존재하지 못한다.
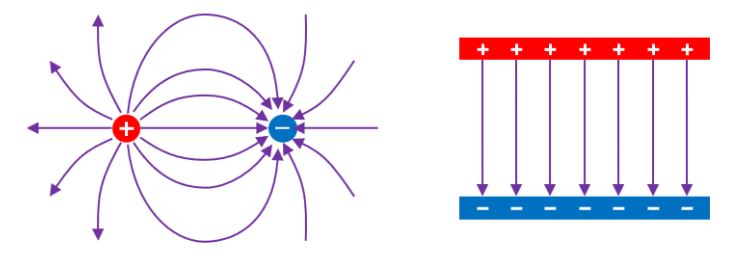
이 두 개의 자극 사이에는 전기의 +, - 극과 마찬가지로 그림 I-23과 같은 성질이 있다.
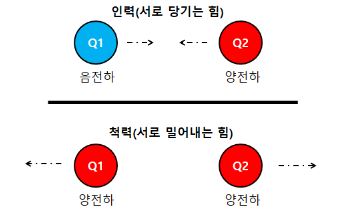
⊙ 같은 자극(N과 N, S와 S)끼리는 서로 반반력이 작용한다.
⊙ 다른 자극(N과 S) 끼리는 서로 반발력이 작용한다.
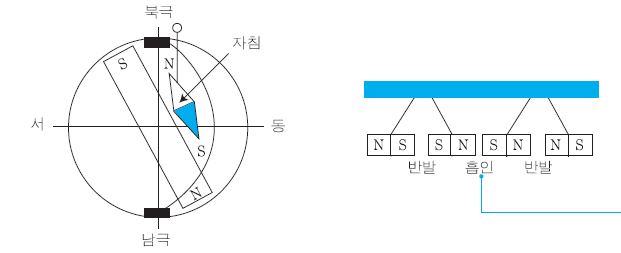
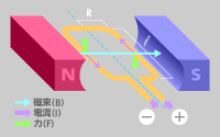
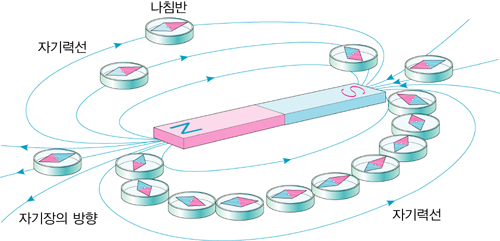
▣ 이 때, 작용하는 힘을 자기력이라 한다. 또한 그림 I-24와 같이 자기력이 작용하는 공간을 자기장(magnetic field) 또는
자장이라고 한다. 자기력이 N극에서 나와 S극으로 들어가는 선을 자기력선이라 한다

나. 자기장
▣ 자기력이 작용하는 자석 주위의 공간을 자기장이라고 한다. 자기장 안의 여러 장소에 나침반을 놓아 보면
장소에 따라 자침이 가리키는 방향이 달라진다. 이때, 자침의 N극이 가리키는 방향을 그 점에서의 자기장의
방향이라고 한다. 또, 자기장 안의 어떤 점에서 표준이 되는 작은 자침의 N극이 받는 힘의 크기를 그 점에서의
자기장의 세기라고 한다. 자기장의 세기는 자극의 세기에 비례하며, 자극에서 멀어질수록 작아진다.
자기장의 방향을 따라 연속적으로 이어 놓은 선을 자기력선이라고 하며 철가루가 늘어선 모양과 같다. 자기력선은
N극에서 나와 S극으로 들어가며, 도중에서 끊어지거나 다른 자기력선과 만나지 않는다.

2. 쿨룽의 법칙 (Coulomb)
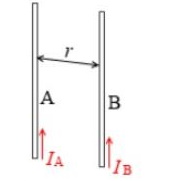
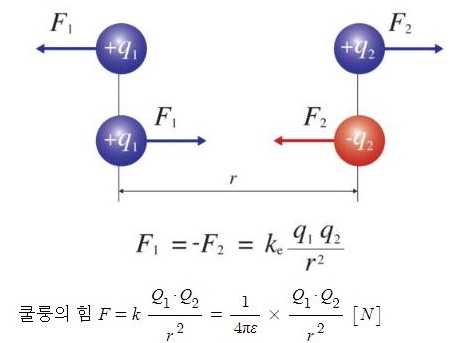
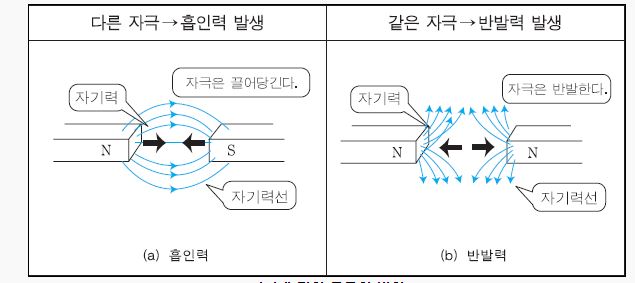
▣ 두 자극 사이에 작용하는 힘의 크기(F)는 두 자극의 세기의 곱에 비례하고, 두 자극 사이의 거리(r)의 제곱에 반비례한다.
▣ 자석이 가지고 있는 자기량을 자하(magnetic charge)라 하며, 단 위로는 웨버[weber : Wb]를 사용한다.두 개의 자극
사이에 작용하는 힘의 방향은 그림과 같이 자극이 서로 다를 때에는 흡인력이, 같을 때에는 반발력이 발생한다.
이 때, 자하 사이에 작용하는 힘의 크기를 나타낸 것을 자기에 관한 쿨롱의 법칙(Coulomb's law)이라 하며,
힘은 두 자하의 곱에 비례하고 거리의 제곱에 반비례한다.
▣ 자기장 내의 쿨룽의 힘 계산

여기서, F : 두 자극 사이에 작용하는 힘(자기력) [N], m1, m2 : 자극의 세기 [Wb],
μ : 투자율[H/m] (μ = μo · μs), μo : 진공의 투자율 (μo = 4π×10-7)[H/m]
μs : 매질의 투자율 (진공, 공기 중 약 1), r : 거리[m] (자극간의 거리)
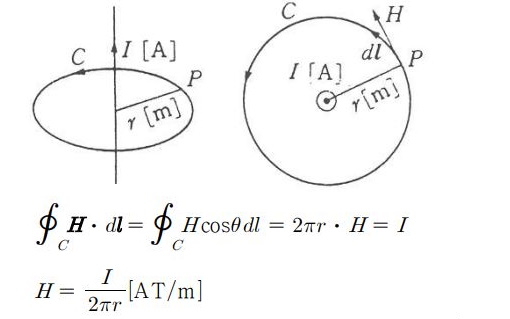
3. 자계 및 자계의 세기
가. 자계 (Magnetic field)
▣ 자력이 작용하는 공간을 자계 또는 자기장, 자장이라 한다.
나. 자계의 세기 (Magnetic field Intensity)
▣ 자계 중에 1[Wb]의 자하를 놓을 때 그 자하에 작용하는 힘을 자계의 세기라고 하고
기호로는 H, 단위는 [At/m], 또는 [N/Wb]로 나타낸다.
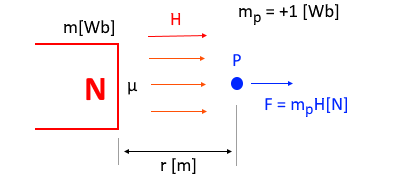
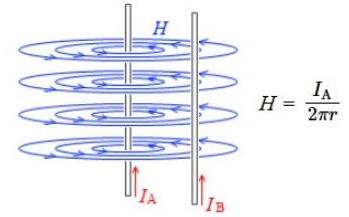
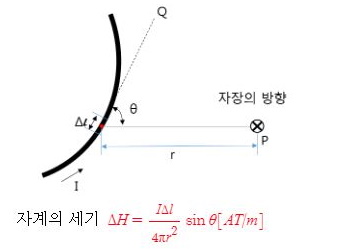
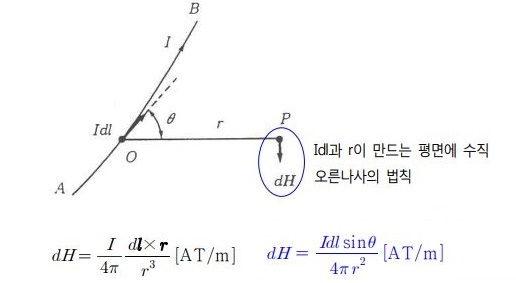
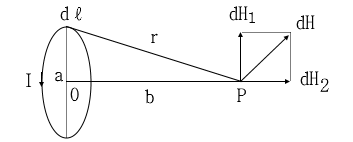
▣ m[Wb]의 자극에서 r[m] 떨어진 점 P에서의 자계의 세기 H[AT/m]은 다음과 같이구할 수 있다.
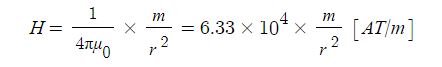
여기서, H:자계의 세기 [AT/m], μ:투자율[H/m] (μ = μo·μs), μo : 진공의 투자율 [H/m],
μs : 비투자율, m : 자극의 세기[Wb], r : 거리 [m]
4. 자계와 자기력과의 관계
▣ 자계의 세기와 쿨룽의 힘, 상호간 관계는 다음 식으로 나타낼 수 있다.

여기서, F : 힘[N], m : 자극의 세기[Wb], H : 자계의 세기 [AT/m]
▣ 자계가 전혀 없는 무한히 먼 장소에서 그 곳까지 도중의 자계에 의한 힘에 저항하여 1[Wb]의 정자극을 운반하는데
필요한 일
▣ 자위 (Magnetic potential) : 정상 자계내의 단위 정자극 m(+1[Wb])을 무한 원점에서 임의의 한 점(P점)까지 운반할 때
소요되는 일 [J/Wb]
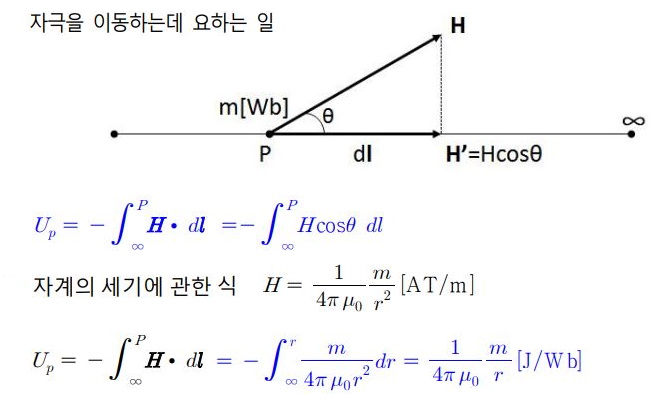
위 산정식을 다음과 같이 사용할 수 있다.
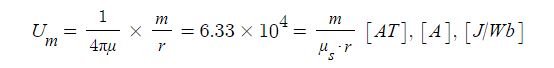
여기서, Um : P점에서의 자위 [AT], μ : 투자율[H/m] (μ = μo· μs), μs : 비투자율, m : 자극의 세기[Wb], r : 거리 [m]
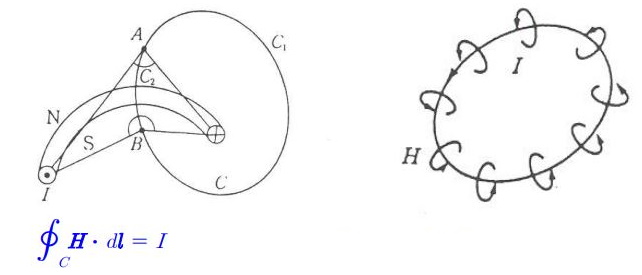
6. 자기력선 (Line of magnetic force)
▣ 자석에서 발생되는 자계의 세기와 방향을 가상적인 선으로 나타낸 것
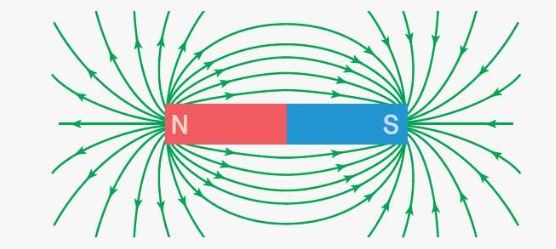
▣ #자기력선 의 성질
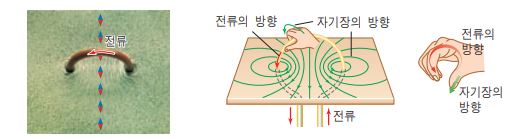
① 자력선은 N극 (정자극)에서 나와 S극 (부자극)으로 들어간다.
② 같은 방향의 자기력선끼리는 서로 반발력이 작용한다.
③ 자력선상의 임의의 한 점에서 자력선의 접선방향이 그 점의 자계의 방향이다.
④ 자계 내의 임의의 한 점에서의 자력선 밀도는 그 점의 자계의 세기를 나타낸다.
⑤ 자극(자하)이 존재하지 않는 곳에서는 자력선이 발생, 소멸이 없고 연속적이다.
⑥ 자력선은 서로 만나거나 교차하지 않는다.
⑦ 자극(자하) m[Wb]에서 m/μ [lines]의 자력선이 발생한다.
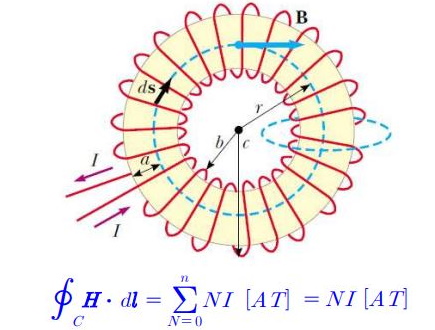
7. 자속과 자속밀도
가. 자속(Magnetic flux)
① 자극에서 나오는 자하의 자력선의 수
② 기호 ф, 단위 [Wb]
나. 자속밀도 (Magnetic flux density)
① 단위면적을 수직으로 지나가는 자기력선의 수
② 기호는 B, 단위는 [G](가우스), [T](테슬라), [Wb/㎡]
다. 자장과 자속밀도와의 관계식
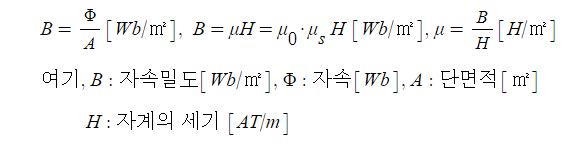
▣ 자극의 세기 m[Wb]와 자석의 길이 l[m]와의 곱을 자기쌍극자모멘트(Magnetic dipole moment)라고 한다.
⊙ M = mℓ [Wb·m]
여기서, M : 자기쌍극자모멘트[Wb·m], m : 자극의 세기 [Wb], ℓ : 자석의 길이[m]
【 정자계 용어 해설】
가. 자기장 (Magnetic field)
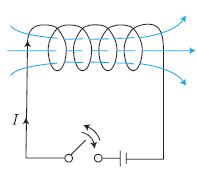
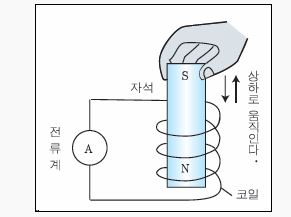
▣ Field(장)란 공간을 의미한다. 자기장이란 자석이 있을 때 이 자석의 힘이 미치는 공간을 말한다. 자석의 힘은 눈에
보이지 않아 그 힘을 쉽게 알 수 없지만 자석 주위에 철가루를 뿌려 보면 자석의 힘이 미치는 공간을 추정해 볼 수 있다.

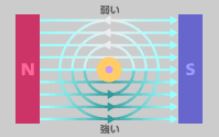
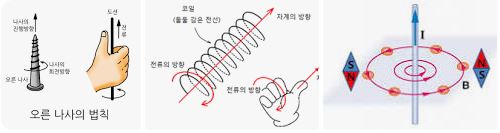
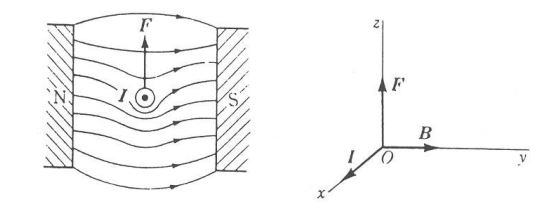
▣ 자기장은 위 그림의 화살표 처럼 N극에서 나와 S극으로 들어가며 양 극 부분에는 자기장의 세기가 크다.
하지만 사실 자기장은 자석이 생김과 동시에 형성되는 것으로 이것이 어디에서 나와 어디로 들어 가는 것은 아니다.
막대자석 주위에 철가루를 뿌려 보면 알 수 있듯이 자기장의 형태에 따라 철가루가 배치되는 모습을 보이지만
자기장이 화살표를 가지고 흐르는 것도 아니므로 실제 자기장의 이동 방향은 알 수 없다.
▣ 사실 자기장의 방향은 아주 오래전에 그렇게 정해졌고 그 방향을 기준으로 모든 법칙이나 원리가 적용되기 때문에
대부분의 서적이나 자료들에는 그렇게 표기하고 있다.
▣ 결론적으로 자기장의 방향을 정해놓으면 그것과 관련된 다른 원리들을 정의내리기 보다 용이하기 때문에 그렇게 하는
것이다.
▣ 실제 자기장의 형태는 N극이나 S극 부터 시작되는 것이 아니라 자석 내부를 거치는 폐루프(Close Loop) 형태로 이루어
진 것이다.
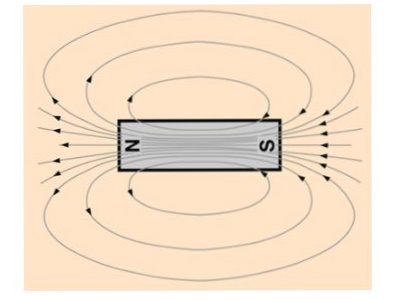
위 그림에서 알 수 있듯이 자기장은 내부와 외부를 거치는 형태로 존재한다. 그리고 자기장의 방향은 자석의 외부에서
보면 N극에서 나와서 S극으로 들어가는 것 처럼 보이지만 자석 내부적으로는 S극에서 N극으로 이동하는 것 처럼 보인다.
나. #자기장 의 세기 (Strength of Magnetic Field)
자기장 자체를 정의하는 것은 비교적 쉽다. 하지만 자기장의 세기를 정의하는 것은 간단하지 않고 그 기준을 잡는데
어려움이 있을 수 있다. 아주 센 힘을 갖는 아래와 같은 자석이 있다고 하자.

이 자석을 철 같은 물질에 가까이 하면 아주 강력한 힘으로 철에 붙을 것이고 우리는 해당 자석의 힘이 강하다고 할 것이다.
그럼 이것이 자기장의 세기에 대한 정의로 맞는 것일까?
일부는 맞다고 할 수 있지만 위와 같은 자석의 자기장의 형태는 아래 그림과 같이 빨간색 화살표 형상으로 철에 붙는 면은
자석의 극(Pole) 즉, 자극(Magnetic Pole)인 부분이다.
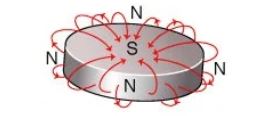
하지만 자석의 힘이 미치는 영역인 자기장은 극 부분에만 있지 않기 때문에 자석이 철에 붙는 힘만으로 자기장 전체의
세기를 나타낸다고 말하기는 곤란한 부분이 있다. 그러므로 자석이 강력하게 철에 붙는 것을 자석 즉, 자기장의 세기가
크다고 하는 것 보다는 이 자석의 자석극의 세기가 크다고 하는 것이 보다 정확한 표현일 것이다.
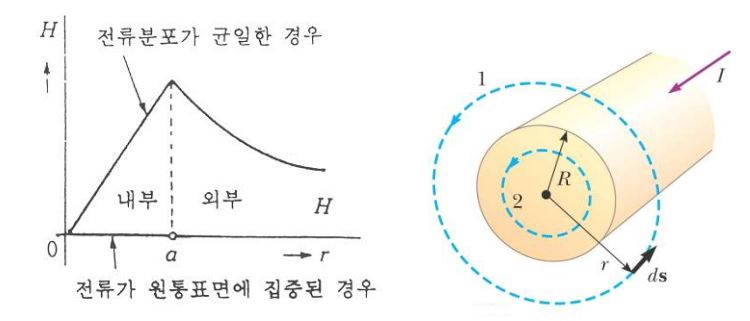
자기장의 세기는 자석 주위의 가상의 선인 자기력선(Magnetic Field Line)을 통해 유추해 볼 수 있다. 자기력선이 촘촘하게
있으면 자기장의 세기가 큰 것이고 자기력선이 듬성듬성 있거나 많지 않으면 자기장의 세기가 약하다고 할 수 있다.

자석의 양 극 부분에는 자기력선이 많기 때문에 자기장의 세기가 크고 그로 인해 자극 부분으로 철이 더 쉽게 붙게 된다.
자기장의 세기는 H로 표기하고 단위는 [AT/m]로 표기한다. 사실 자석에서 뿜어져 나오는 전체 자기장의 또는 자기력선의
수를 세는 것은 불가능하다. 그러므로 일반적으로 자석의 극의 세기를 자기장의 세기라고 표현할 때도 있지만 그 보다는
다른 용어를 사용하기도 한다. 그것이 바로 자속밀도라는 개념이다.
다. 자속(Magnetic Flux)
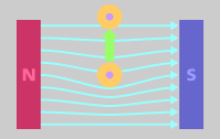
자석 주위에는 자기장이 있고 이 자기장은 자기력선의 분포량을 통해 그 세기를 어느 정도 가름할 수 있다. 하지만 자석
주위의 자기장이 모두 유효한 것은 아니다. 자기장 중 보다 유효한 자기장은 어떤 물질을 자기장 내에 넣었을 때 그 물질을
통과하는 자기장이다. 전체 자기장 중 물질의 단면적을 통과하는 자기장, 다시 말해 물질의 단면적을 통과하는 자기력
선의 수를 #자속 ( #Magnetic #Flux )이라고 한다. 자속의 경우 자기장 보다는 해당 물질에 더욱 주안점을 둔 정의로 물질
주위에 많은 자기력선이 있지만 그 많은 자기력선 중에 물질 내부를 통과하는 자기력선만을 나타낸 것으로
아래 그림과 같은 선들을 말한다.
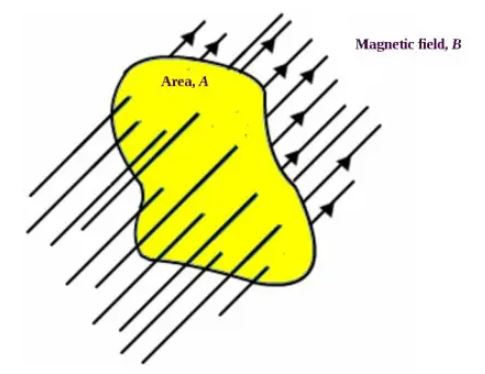
자속의 기호는 ф(파이) 또는 фB라고 하며 단위는 Wb(웨버, Webber)를 사용한다.
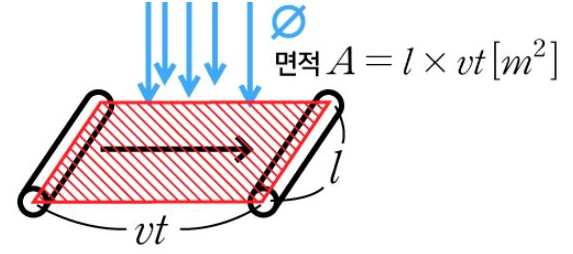
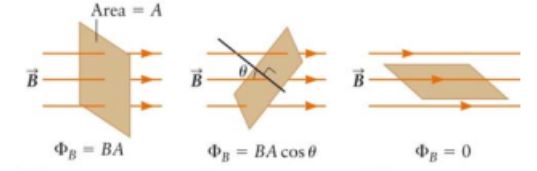
자속의 경우 해당 물질의 단면적과 수직으로 만날 때가 가장 많고 각도를 가지면서 만나면 그 수량이 줄어들기 때문에
수직으로 만날 때는 자속의 수식은 ф=BA이고 각도를 가지고 만날 때는 ф = BAcosθ가 된다. 여기서 A는 해당 물질의
단면적이고 B는 자속밀도를 의미 하지만 자속밀도는 아래에서 설명한다.
라. 자속밀도 (Magnetic Flux Density)
자속밀도는 자속을 이해하면 좀 더 쉽게 이해할 수 있다. 자속밀도(Magnetic Flux Density)는 자속의 밀도 즉, 자속의
촘촘함의 정도를 말한다. 자속(Magnetic Flux)의 밀도이기 때문에 자기장의 세기와 혼동하면 안된다. 자기장의 세기는
자석이 뿜어내고 있는 전체적인 자기력선의 세기를 의미하고 자속은 그 많은 자기력선 중 어떤 물질의 단면적을 통과하기
위해서 물질 내부로 들어 온 자기력선의 수만을 의미한다.
자속밀도는 이렇게 물질내로 들어온 자기력선의 수를 단위 면적(㎡)으로 나눈 값이며 기호는 B를 쓴다. 자속밀도와
자속과의 관계는 앞서 설명한 ф=BA라는 수식을 그대로 사용하면 되고 B를 기준으로 정리하면 자속밀도 B=ф/A가 된다.
물론 자기장이 각도를 가지고 해당 물질을 통과하면 이 때의 자속밀도는 ф=BAcosθ의 수식이 적용된다.
자속밀도는 때론 자기장의 세기를 나타내는 값으로도 사용되기도 하지만 보통 B Field(자속밀도)나 H Field(자기장의 세기)
등으로 표현하기도 한다. 자속밀도의 단위는 #테슬라 (τ) 이다. 그렇다. 기호는 테슬라이다. 테슬라라는 것은 현재 엘론
머스크가 운영하고 있는 전기자동차 회사의 이름이다. 사실 테슬라는 니콜라 테슬라라는 사람의 이름에서 따온 것으로
테슬라는 유도 전동기(Induction Motor)를 고안해 낸 아주 유명한 전기분야 과학자이다.

자속밀도와 자기장의 세기와의 관계는 B= μH와 같고 여기에서 μ는 물질의 투자율이다. 투자율이란 물질이 자기장안에
놓였을 때 자화 즉, 자석화되는 정도를 의미하며 투자율이 높을 수록 자속밀도도 커지게 된다. 일정한 자기장의 세기 H가
있을 때 투자율이 높으면 더 많은 자기력선을 끌여 들일 수 있기 때문에 자속밀도 B값이 커지게 된다.
1τ(테슬라)는 1[Wb/㎡]를 의미하는데 그 값은 B=ф/A 수식을 통해서 구해진다. 자속 ф의 단위가 Wb이고 면적 A의 단위는
㎡이니 그것을 그대로 적용하면 Wb/㎡가 된다.
1τ(테슬라)는 대단히 큰 값이다. 우리가 냉장고에 붙이는 자석이 대략 0.001[τ] 정도를 가지고 있고 지구의 자기장은
대략 0.00005[τ] 정도이다. 1[τ] 정도면 트럭도 들어 올릴 수 있는 힘이라고 하는데 정확하지는 않다. MRI장비에 사용되는
자기장의 세기는 보통 1.5[τ] 또는 3.0[τ] 정도이고 이 장비가 발생시키는 자기장의 세기는 대단히 강력한 것이기 때문에
만약 철과 같은 자성이 있는 물질을 가지고 MRI검사를 하면 심각한 사고가 발생할 수 있다.
【 출제 예상 문제 】
1. 공기중에서 3×10-4 [Wb]와 5×10-3[Wb]의 두 극 사이에 작용하는 힘이 13[N]이었 다. 두 극 사이의 거리는
약 몇 [㎝]인가 ? ②
① 4.3 ② 8.5 ③ 13 ④ 17
[해설] 두 자극 사이에 작용하는 힘
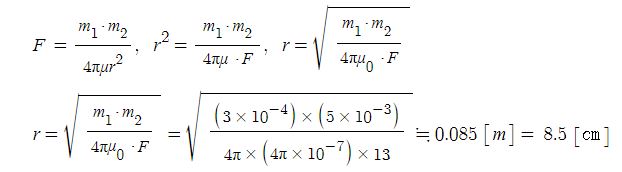
2. 두 자극 간의 거리를 2배로 하면 자극 사이에 작용하는 힘은 어떻게 되는가 ? ④
① 2배가 된다. ② 4배가 된다. ③ 1/2배가 된다. ④ 1/4배가 된다.
[해설] #쿨룽 의 법칙
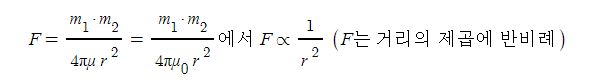
3. 단면적 4[㎠]의 철심에 6×10-4[Wb]의 자속을 통하게 하려면 2,800[AT/m]의 자계가 필요하다. 이 철심의 비투자율은
대략 얼마인가 ? ④
① 346 ② 375 ③ 407 ④ 427
[해설] #비투자율
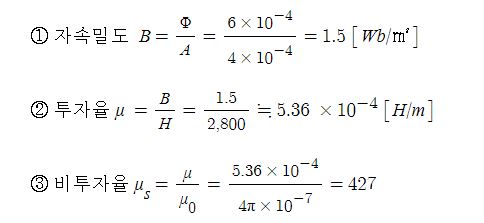
4. 자극의 세기 m = 4[Wb]의 점 자극으로 부터 r=4[m] 떨어진 점의 자계의 세기 [A/m]를 구하면 ? ③

5. #진공 중의 자계 10[AT/m]인 점은 5×10-3 [Wb]의 #자극 을 놓으면 그 자극에 작용하는 힘[N]은 ? ①
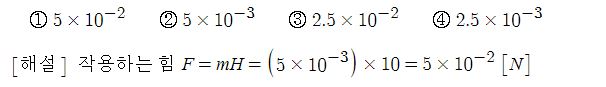
6. 비투자율이 160인 철심을 사용한 환상솔레노이드에서 철심 속의 자계의 세기가 80[AT/m] 일 때 철심 속의 자속밀도는
약 몇 [Wb/㎡]인가 ? ②
① 0.008 ② 0.016 ③ 0.032 ④ 0.064
[해설] #자속밀도 B = μH = μoμsH = (4π × 10-7)×160×80 ≒0.016[Wb/㎡]