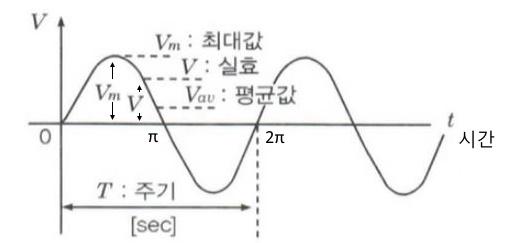
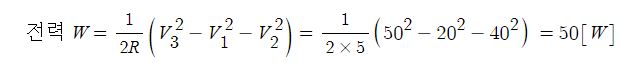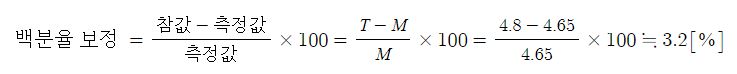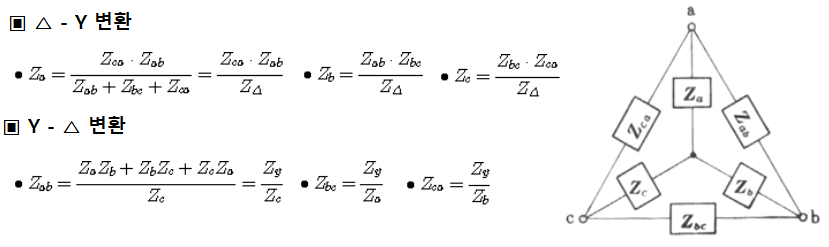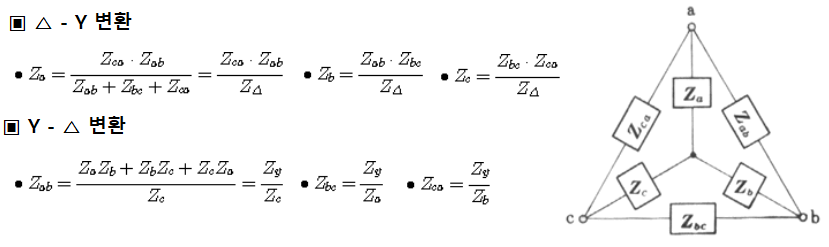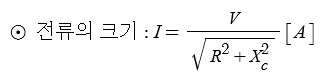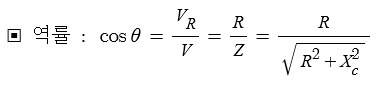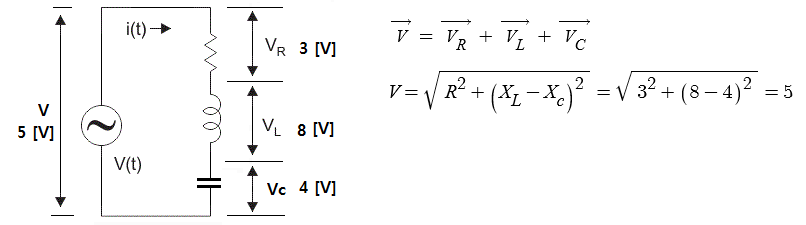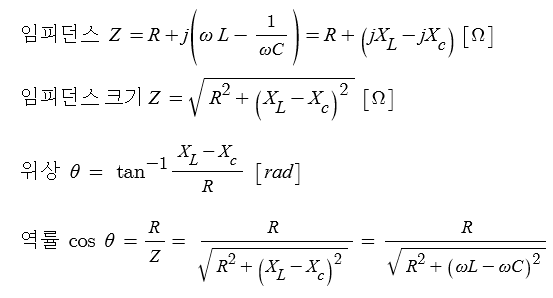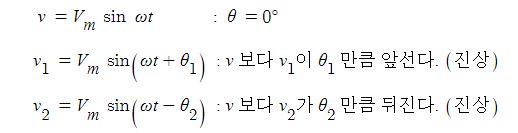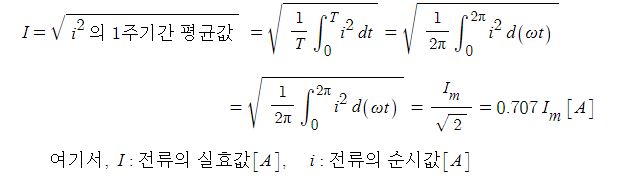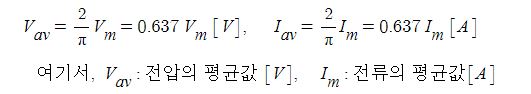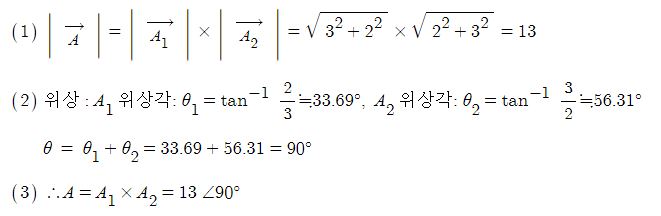1. 정전압원, 정전류원
가. 선형회로망
▣ R ( #저항 ), L( #인덕턴스 ), C( #커패시턴스 ), G( #컨덕턴스 ) 등의 회로 소자가 전압, 전류에 따라 그 본래의 값이
변하지 않는 것을 선형소자라 하며, 이들 선형소자로 구성된 회로를 #선형회로망 이라 한다.
나. 전압원
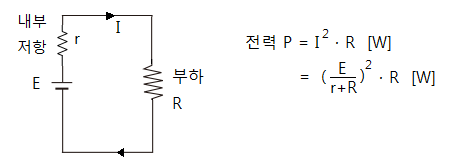
▣ 부하에 흐르는 전류 크기와 관계없이 항상 전압원의 기전력과 같은 전압을 부하에 일정하게 공급하는 기능을 가진
전원으로 이상적인 전압원은 내부 저항이 적을수록 좋다.
※ 이상적인 전압원 : 내부 임피던스 Z = 0
다. 전류원
▣ 부하의 변동에 관계없이 항상 일정한 전류를 공급하는 전원장치로서 부하 전압의 변화에 대해서도 항상 일정한 전류가
유지되도록 공급하는 기능을 가진 전원으로 이상적인 전류원은 내부 저항이 클 수록 좋다.
※ 이상적인 전류원 : 내부 #임피던스 Z = ∞
2. 중첩의 원리
▣ 전압원, 전류원이 여러 개 존재하는 회로망에서 각각의 지로(소자)에 흐르는 전류는 각 전원(전압원, 전류원)을
단독으로 작용하고 있는 각 지로(소자) 전류의 총합과 같다.
가. 전원의 변환
▣ 전원의 변환은 전압원과 전류원을 상호 등가 변환하는 것이다. #전압원 은 #부하 에 직렬로 연결하고 전류원은 부하에

▣ 복합한 회로를 하나의 전압원과 하나의 임피던스(저항)로, 또는 하나의 전류원과 하나의 임피던스(저항)으로 단순화할
수 있는데, 이 때 전압원 회로와 전류원 회로는 등가이고 하나의 전압원과 임피던스로 단순화하는 것을 #데브난 의
정리라고 하고 하나의 전류원과 하나의 임피던스(저항)으로 단순화하는 것을 #노턴 정리라고 한다.
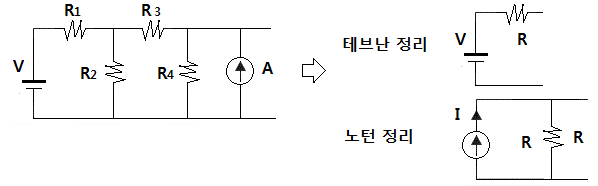
※ 전원변환을 연습하여 보자.
⊙ 전원변환은 전압원은 직렬로 연결하고 전류원은 병렬로 연결한다. 전압원의 전압과 전류원의 전류는 오옴의 법칙에
따라 산정하여 변환하고 임피던스(저항)은 값을 그대로 하고 회로를 직렬과 병렬로 각각 변환한다.
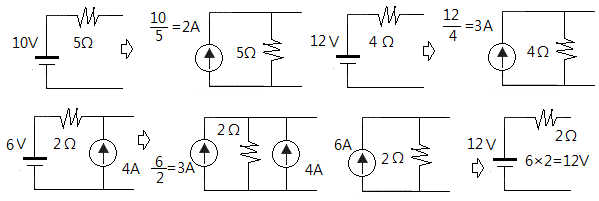
가. 중첩의 원리를 이용한 회로 해석 순서
① 한 개의 전원 (전압원이나 전류원)을 취하고 나머지 전원은 모두 없앤다.
(이 때, 전압원은 단락, 전류원은 개방시킨다)
② 그 전원 만에 의해 지로(소자)에 흐르는 전류를 구한다.
③ 그 다음 전원을 취하여 전원 수 만큼 이전 단계를 반복한다.
④ 구하려는 지로(소자)의 전류는 각각의 전원에 의해 구한 전류값을 대수적으로 합하여 구하는데,
이 때 전류의 방향이 같은 것은 (+)하고 다른 것은 (-)로 한다.
⊙ 중첩의 원리는 회로가 선형회로라고 가정하고 간략화한다. 선형회로라면 각각의 전원을 기준으로 회로를
단순화할 수 있고 단순화된 회로를 더하면 합성 회로가 된다는 원리를 이용한 것이다.
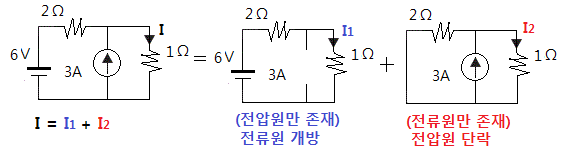
※ 전압원만의 회로를 구할 때는 전류원은 저항이 무한대(∞)이므로 회로를 개방하고
전류원만의 회로를 구할 때는 전압원은 저항이 "0"이므로 회로를 단락한다.
◈ 예를 들어 아래의 회로를 중첩을 원리에 따라 회로를 합성하여 보자.

① 전압원만 있을 때의 합성저항을 구할 때는 전류원을 개방하고 전압원의 반대쪽에서 부터 합성저항을 구한다.
합성저항을 구한 다음 전체 전류를 구하고 이 합성전류를 회로 저항에 배분한다.
㉠ 전압원만의 회로에서는 전체 전류를 구하기 위하여 각각의 저항을 모두 합성한다.
㉡ 전체 전류를 It = 2 [A]를 구한 다음에는 전류 I를 구하기 위해서는 전체전류 2[A]가 저항2[Ω]과 저항 1 [Ω]+ 저항 1[Ω]
인 병렬회로에 분기하므로 구하고자 하는 전류 I = 2[Ω] / (1[Ω]+1[Ω]+2[Ω]) × 2[A] = 1[A]가 된다.
② 전류원만 있을 때의 합성 저항은 전압원을 단락하고 전류원의 반대쪽에서 부터 회로를 분석하여 합성 저항을 구한
다음 전체 전류를 구하고 각각의 저항이 있는 분기에 전류를 분배한다.
㉠ 구하고자 하는 전류 I 를 중심으로 각 분기의 저항을 합성한다.
㉡ 전류 I 는 전체 전류 9[A]가 저항 1[Ω]+1[Ω]의 분기와 저항 1[Ω]의 분기가 병렬로 연결된 회로에 흐르므로 전류 I는
[1[Ω] / (1[Ω]+1[Ω]0+1[Ω]] × 9[A] = 3[A]이다.
그런데 전류의 방향이 반대이므로 -3[A]가 된다.
③ 이제 합성전류는 전압원만의 전류와 전류원만의 전류를 더하면 된다.
∴ 합성전류 I = I1+I2 = 1+ (-3) = -2[A] 이다.
3. 테브난의 정리 (등가전압원 정리) (Thevenin's theorem)
▣ #테브난 정리는 복잡한 회로를 간단하게 할 때 사용하는 것으로 하나의 전압원과 하나의 임피던스(저항)으로 표시하는
방법이다.
▣ 테브난 정리에 들어가기에 앞서 개방된 회로의 #전압 관계에 대해 알아보자.
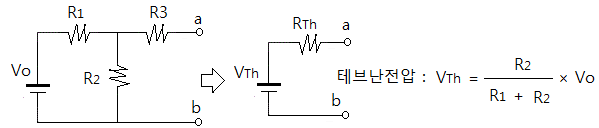
⊙ 테브난 전압은 위와 같이 구하고, 테브난 저항은 다음과 같이 구한다.
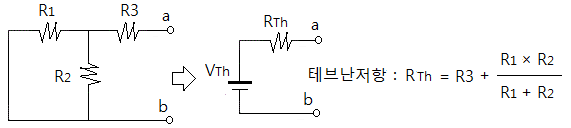
※ 테브난 저항은 전압원을 단락시키고 a, b 단자에서 바라본 합성저항을 말한다.
예제 : 다음 회로를 테브난의 정리에 의해 단순화 해 보자.
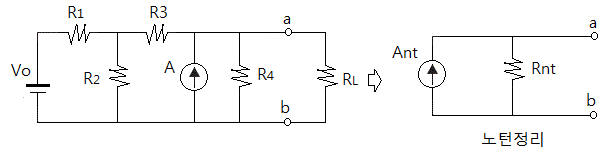
예제 : 다음 회로를 테브난 회로로 변환하여 보자.

▣ 노턴의 전류는 a, b단자를 단락시킨 후 a, b단자간에 흐르는 전류인데 a, b 단자간을 단락을 시키면 저항이 "0"이므로
모든 전류가 단락지점으로 흐르게 되어 전류원의 6[A]가 모두 흐르게 된다. 노턴의 저항은 a,b 단자에서 바라본
저항으로 전류원은 개방하므로 전류원 쪽으로는 전류가 흐르지 않아 3[Ω]은 합성저항에 포함되지 않는다.
가. 전원 변환 : 테브난 ⇔ 노턴
▣ 테브난 회로와 노턴 회로는 쌍대 관계가 있어 상호 서로 등가변환할 수 있다.
⊙ 전원 등가변환은 오옴의 법칙에 따라 전압원 전압과 전류원 전류를 구하고 전압원에는 직렬저항을 연결하고
전류원에는 병렬저항을 연결한다.
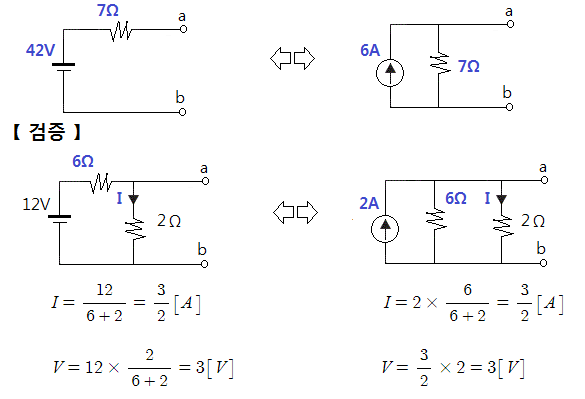
예제 : 아래 회로에서 테브난을 이용하여 VR을 구하고 노튼을 이용하여 IR을 구하여라.

5. 밀만의 정리
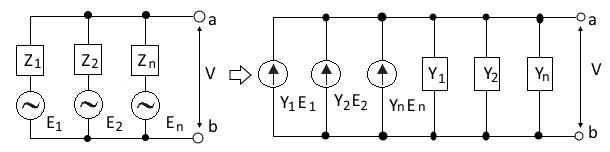
다수 전압원이 병렬로 접속된 단자에 걸리는 전압을 계산할 때는 임피던스를 가진 전압원이
거의 병렬로 연결되어 있을 때 단자 a, b에 나타나는 전압 Vab는 다음과 같다.

여기서 전압원이 없는 임피던스는 전압원의 값을 0으로 계산한다.
【 출제 예상 문제】
1. 여러개의 기전력을 포함하는 선형회로망 내의 전류분포는 각 기전력이 단독으로 그 위치 에 있을 때 흐르는
전류분포의 합과 같다는 것은 ? ②
① 키르히호프의 법칙 ② 중첩의 원리 ③ 테브난의 정리 ④ 노튼의 정리
[해설] 중첩의 원리 : ⊙ 2개 이상의 기전력을 포함한 회로 중의 어떤 점의 전위 또는 전류는 각 기전력이 각각 단독으로
존재한다고 할 때 그 점의 전위 또는 전류의 합과 같다는 원리
⊙ 여러개의 기전력을 포함하는 선형회로망 내의 전류분포는 각 기전력이 단독으로 그 위치에 있을 때 흐르는
전류의 합과 같다는 원리
2. 그림에서 저항 20[Ω]에 흐르는 전류는 몇 [A]인가 ? ③
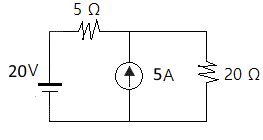
① 0.8 [A] ② 1.0 [A] ③ 1.8 [A] ④ 2.8 [A]
[해설]
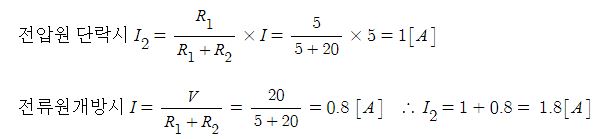
3. 그림에서 R=5[Ω]을 흐르는 전류의 크기 [A]는 ?
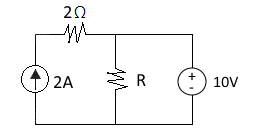
① 1 ② 2 ③ 3 ④ 4
[해설] 중첩의 원리
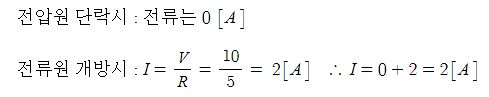
4. 테브난의 정리를 써서 그림 (a)의 회로를 그림 (b)와 같은 등가회로로 만들고자 한다. E[V]와 R[Ω]을 구하면 ? ①
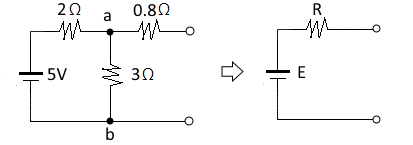
① 3, 2 ② 5, 2 ③ 5, 5 ④ 3, 1.2
[해설] 테브난의 정리

5. 그림의 (a)와 (b)의 회로가 등가 회로가 되기 위한 전류원 I [A]와 임피던스 Z[Ω]의 값은 ? ①
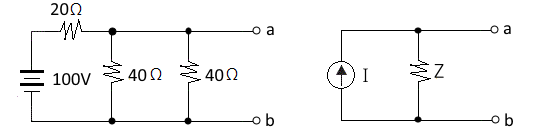
① 5[A], 10[Ω] ② 2.5[A], 10[Ω] ③ 5[A], 20 [Ω] ④ 2.5[A], 20[Ω]
[해설] 노튼의 정리

6. 그림에서 단자 a, b에 나타나는 Vab는 몇 V인가 ?
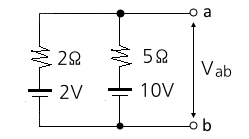
① 3.3 ② 4.3 ③ 5.3 ④ 6
[해설] 밀만의 정리

7. 이상적인 전압원 및 전류원에 대한 설명이 옳은 것은 ? ②
① 전압원의 내부저항은 ∞이고, 전류원은 0이다.
② 전압원의 내부저항은 0이고, 전류원은 ∞이다.
③ 전압원이나 전류원의 내부저항은 흐르는 전류에 따라 변한다.
④ 전압원의 내부저항은 일정하고, 전류원의 내부저항은 일정하지 않다.
[해설] 이상적인 전압, 전류원
⊙ 정전압원의 내부저항 : 0, 정전류원의 내부저항 : ∞
'소방설비기사 (전기) > 소방전기일반' 카테고리의 다른 글
| 영상 임피던스와 분포정수회로 (2) | 2023.02.20 |
|---|---|
| 단자망, 정·역회로, 영점과 극점, 4단자 파라미터.. (0) | 2023.02.20 |
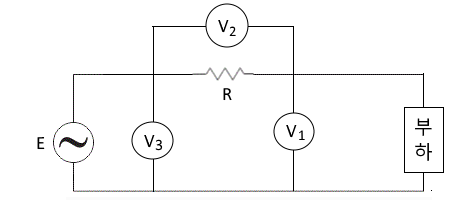
| 교류 전력 측정, 계측기 오차 보정 (2) | 2023.02.16 |
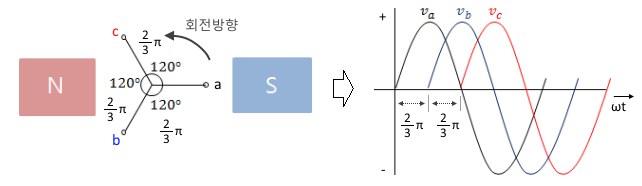
| 3상, n상 교류 전력, Y-△ 결선 임피던스 변환 (0) | 2023.02.14 |
| 교류 전력, 역률, 최대 전력 공급조건.. (0) | 2023.02.13 |