아낌없이 주는 나무

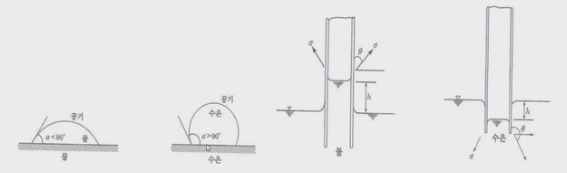
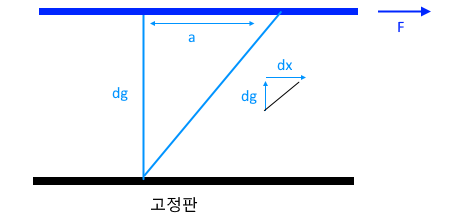
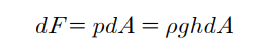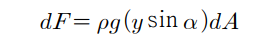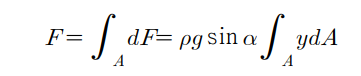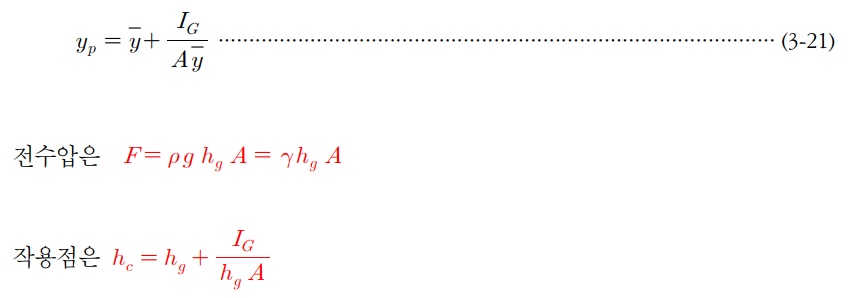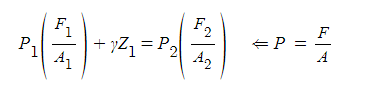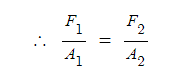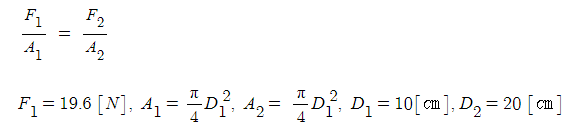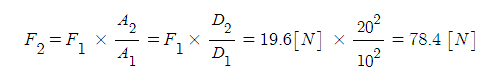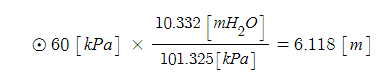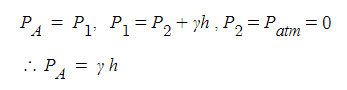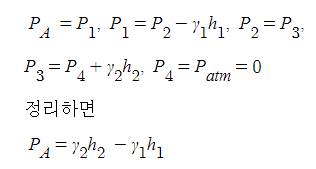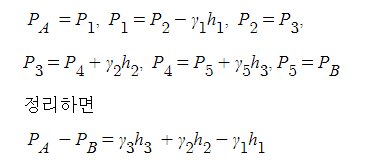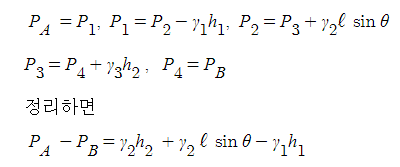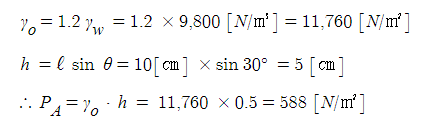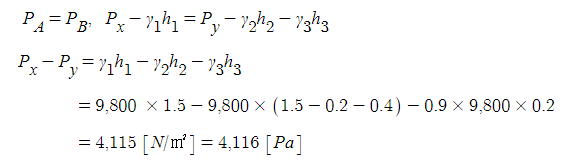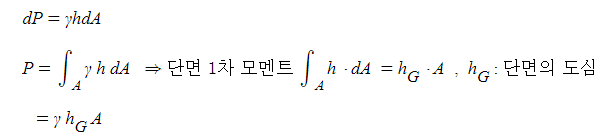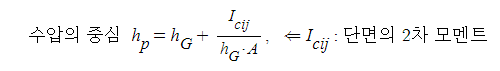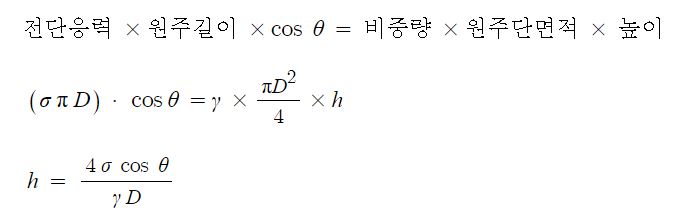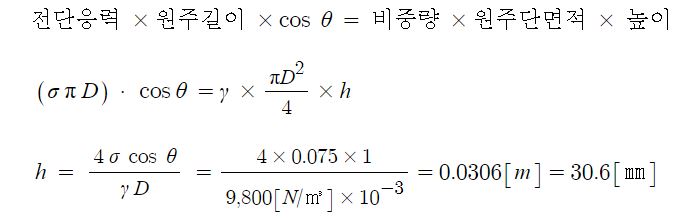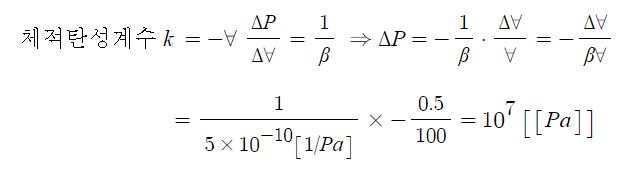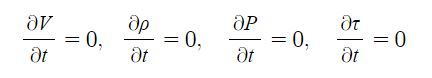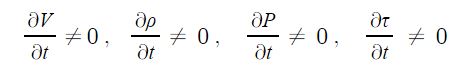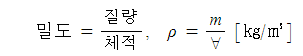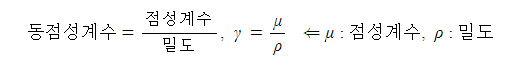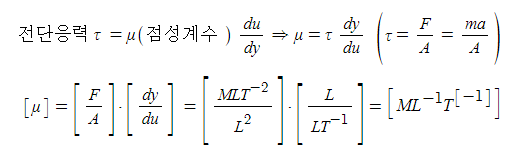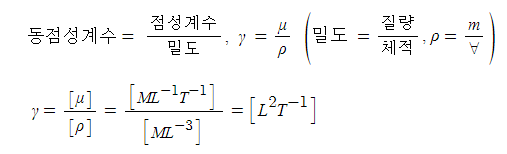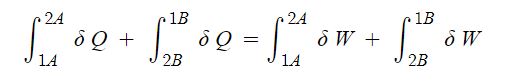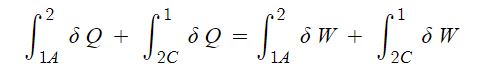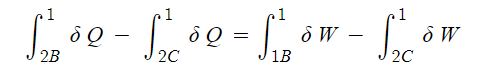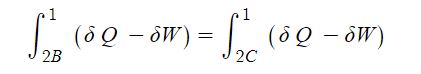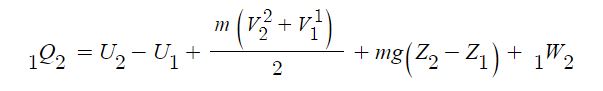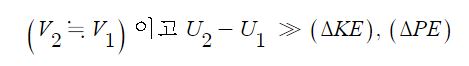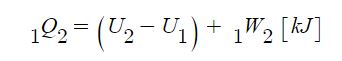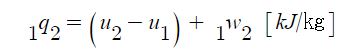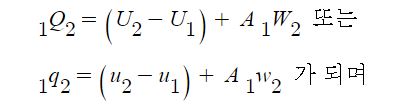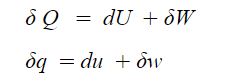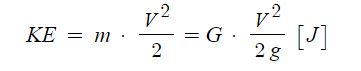1. 정지하는 있는 유체의 전단응력은 "0"이다. 힘은 질량 × 가속도 인데 가속도가 "0"이므로, 그런데 힘은 가속도와 관련이

     있으므로 유체가 동일한 속도로 움직인다면 마찰력이 없다고 하면 이 때도 전단응력은 "0"이 된다.

​

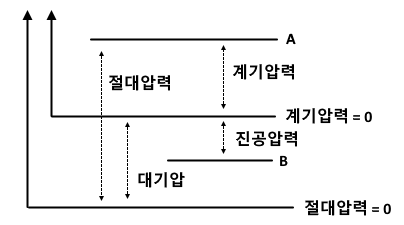
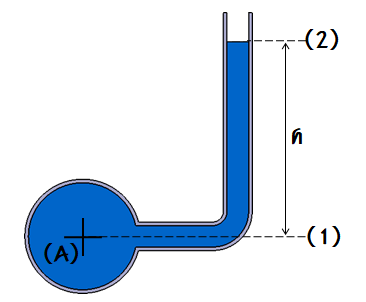
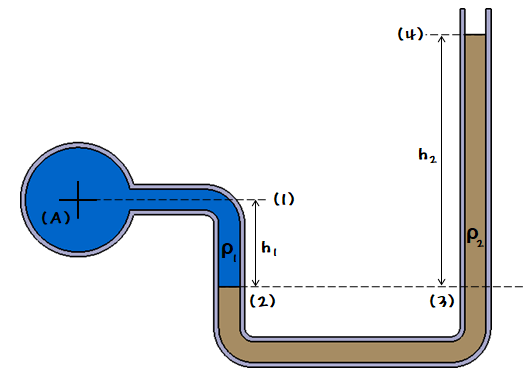
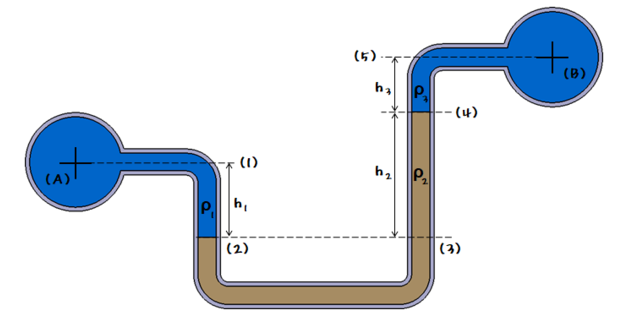
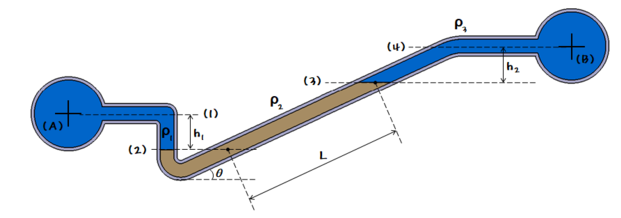
2. 정수압 강도 1[㎏/㎠]를 압력수두로 나타내시오.

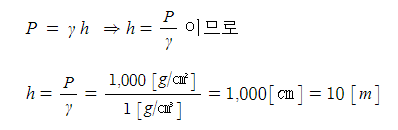
가. 경사평면의 정수압

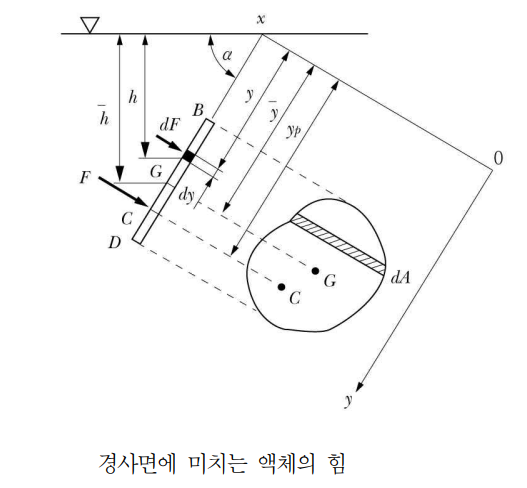
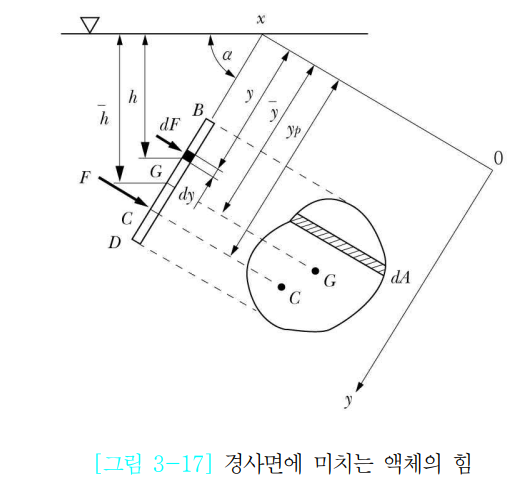
▣ 경사평면에 작용하는 힘은 평면의 도심에 작용하는 힘에 평면 면적을 곱하여 산정한다.

     도심은 수직면으로 보았을 때 작용하는 힘의 평균점이므로 그 점에 작용하는 힘에 면적을 곱하면 그 면에 작용하는

     전체의 힘이 된다.

 ① 전수압​

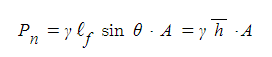
 ② 수압의 위치

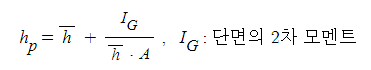
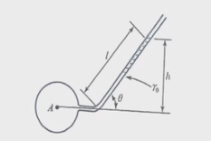
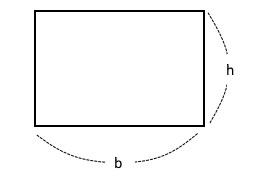
ex. 그림에서 폭 1[m]의 직사각형 평판이 수면과 45˚ 기울어져 물에 잠겨 있다. 한 쪽 면에

작용하는 유체력의 크기 [F]와 작용점의 위치 (yf)는 각각 얼마인가 ?

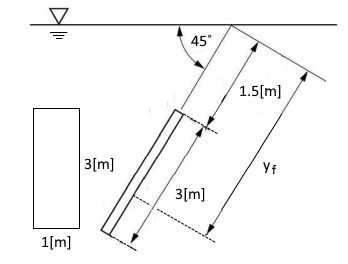
① 유체력의 크기 F = PA = γyf sin θ · A​

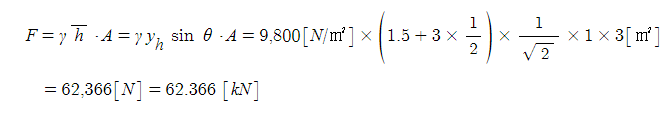
② 힘의 작용하는 점​

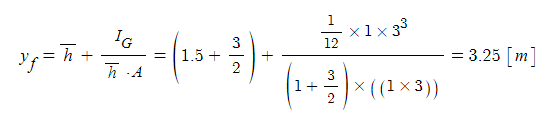
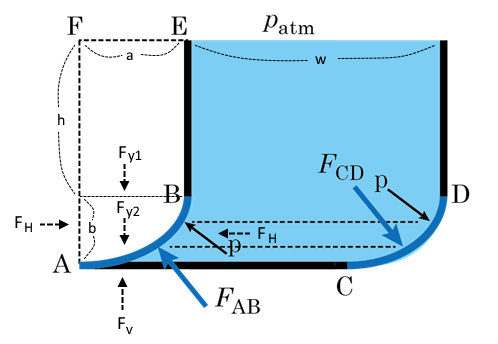
나. 곡면에 작용하는 정수압

 ① 곡면에 작용하는 수압의 면직분력은 곡면을 밑면으로 하는 연직 물기둥의 무게와 같고 그 작용점은 물기둥의 무게 중심

      을 통과하는 연직선이다.

 ② 곡면에 작용하는 수압의 수평분력은 연직 투영면 상태의 투영된 투영면상에 작용하는 수압과 같고 그 작용선도 이 경우

      와 같다.

▣ 수압의 연직분력

 ⊙ 곡면의 물기둥 즉 Fy1의 물기둥 직육면체와 Fy2 곡면의 물기둥의 중량의 합과 같다.​

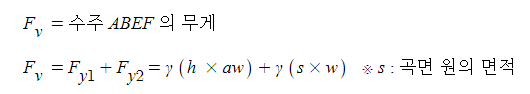
▣ 수평분력

  ⊙ 곡면의 투영된 수직평면의 정수압과 같다.

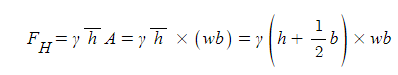
▣ 힘의 작용점

※ 밀도가 일정한데 도심과 무게 중심이 다른 것은 곡면에 힘이 작용하는 각도 때문에 발생하게 된다.​

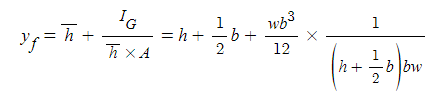
ex 1. 물 탱크의 수직 벽면에 반구형 곡면을 물에 완전히 잠기도록 설치할 때 곡면이 물쪽으로 볼록한 경우와 오목한 경우

          에 곡면에 작용하는 정수력의 수평방향 크기의 비는 ?

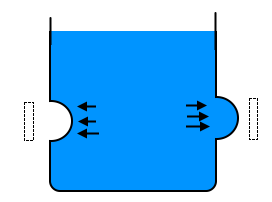
곡면에 작용하는 힘은 투영된 수직평면에 작용하는 힘과 같다.

따라서 힘 : FA = γ h A 이므로 두 곡면에 작용하는 힘은 크기가 같다.

따라서 1 : 1 이다.

​

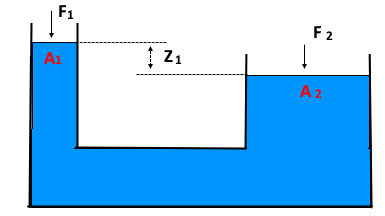
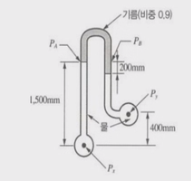
ex 2. 그림과 같은 수문 A, B 가 받는 수평 성분 Fh와 수직성분 Fv 는 각각 약 몇 [N] 인가?

① 수평분력​

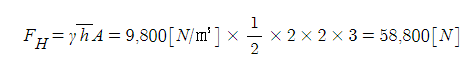
② 수직분력 : γ V(체적) : 물기둥 무게​

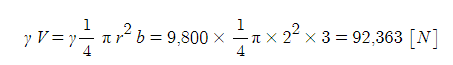
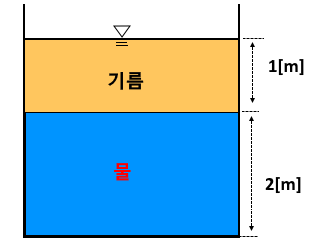
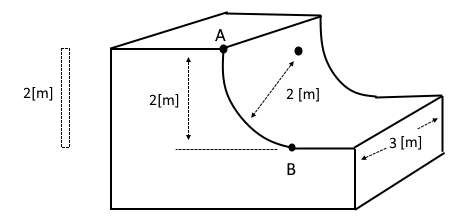
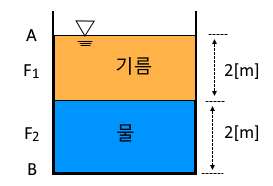
ex3. 그림과 같이 밑면이 2[m] × 2[m] 인 탱크에 비중이 0.8 인 기름과 물이 각각 2[m] 씩 채워져 있다. 기름과 물이 벽면 A,

        B에 작용하는 힘은 약 몇 [kN]인가 ?

① 기름 분력​

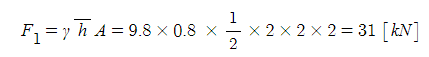
② 물 분력​

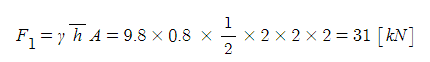
③ 총 힘 : F = F1 + F2 = 70 [kN]

​

ex4. 그림에서 AB 면에 작용하는 수직분력은 약 몇 [kN]인가 ?

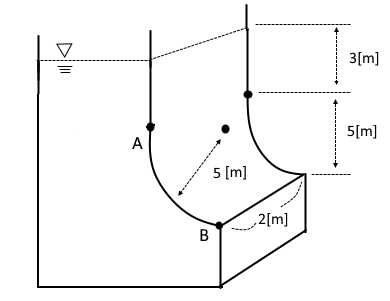
▣ 수직분력 Fv = γ V​

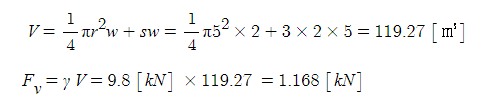
#정수압 #경사면 #곡면 #무게중심 #도심 #투영면 #수평분력 #수직분력 #압력 #수압

[그림 3-17]에서 액체의 자유표면과 α의 경사각을 갖는 경사 평면 BD에 대해서 평면 BD의 한쪽 면에 작용하는 전압력을 구한다. 그의 평면내의 미소면적 dA인 곳의 깊이를 h라고 하면 그 부분의 면 dA의 압력은 ρgh이므로 미소면적 dA에 작용하는 전압력 dF는

로 주어진다.

또한 경사평면 벽의 연장선과 자유표면과의 교점이 이루는 0y축과 그 평면에 직 각으로 0x축을 취한다.

그런데 경사면 미소면적의 깊이는 h = y sin α 이므로 경사면 미소 면적에 작용하는 힘은

압력 × 면적이므로

이 되고

경사 평면벽의 전체면적 A에 작용하는 전압력 F는 미소면적에 작용하는 힘을 전체 면적에 대하여 적분을 하면 얻을 수 있으므로

가 된다.

인 관계가 있다.

​

여기서 y바는 축으로부터 면적의 도심까지의 거리이다.

위 식을 정리하면

전압력 F의 중심인 작용점 yp는 평면의 중심 G 지나는 축에 대한 관성 능률을 IG라 하면 다음 과 같이 된다.

#정수역학 #경사면 #압력 #도심 #무게중심 #관성능률

1. 정수압

​

가. 정수압 기본식

  ▣ 정수압 : 정지하고 있는 유체 (수중 또는 공기)의 용기 내측에 작용하는 유체의 압력  (면에 수직으로 작용)

  ▣ 정수압의 강도​

  ▣ 정지하고 있는 수중의 한 점에 있어서의 정수압의 강도는 면의 방향에 관계없이 일정하다.

    ⊙ 압력 P = γ Z + Pa

         여기서, γ 비중량, Z : 높이 · 깊이, Pa : 대기압 (0 [atm])

  ※ 수평방향으로는 압력이 일정하다.

  ※ 정수중의 한점에 작용하는 정수압의 크기는 모든 방향으로 일정한(같은) 값을 가진다.

  ※ 절대압력 = 대기압력 + 계기압력

​

ex1. 개방된 물통속에 물이 담겨져 있으며 깊이는 2[m] 이다. 이 물 위에는 비중이 0.8인 기름이 1[m] 깊이로 떠 있다.

         기름과 물의 접촉면에서의 압력과 물통 밑바닥에서의 압력을 계산하라.

 ① 접촉면에서의 압력 : 깊이 Z = 1[m]

   ⊙ 압력 P = γ Z = (0.8 × 9,800[N/㎥]) × 1 [m] = 7,840 [N/㎡]​

 ② 물통 바닥에서의 정수압 : 기름의 압력 + 물의 압력

       7,840 +9,800 × 2 = 27,440 [N/㎡]

​

ex2. 수심 3,000[m] 의 해저에 있어서의 정수압을 구하라. 단, 해수의 비중은 1.025이다.

         γ = 1.025 × 9,800 [N/㎥] 이므로

         P = 1.025 × 9,800 [N/㎡] × 3,000 [m] =30,135,000[N/㎡] =30,135 [kN/㎡]

​

나. 수압의 전달​

 ▣ 파스칼(Pascal)의 원리 : 정지상태의 유체 내부에 작용하는 압력은 작용하는 방향에 관계없이 일정하며 그 압력은

                                             유체 내부에 고르게 전달된다.

  ※ 수압기의 원리

  수식으로 나타내면​

  ※ F1, F2를 크게 증가시키면 γZ1은 상대적으로 미소하므로 무시 가능하다.​

  ▣ 단면적의 비를 크게 하면 작은 힘 F1 으로 큰 힘 F2를 얻을 수 있다.

​

ex1. 수압기에서 피스톤의 지름이 각각 20 [㎝], 10 [㎝]이다. 작은 피스톤에 19.6 [N]의 힘을 가하면 큰 피스톤에는 몇 [N]의

        하중을 가하게 되는가 ?​

  위 식을 이용하여 다음과 같이 정리할 수 있다.​

다. 압력의 측정과 단위

  ▣ 절대압력 = 국지 대기압 + 계기압력

       Pabs = Pa + Pg

       Pabs : 절대압력, Pa : 국지 대기압, Pg : 계기압력 (if Pg < 0 이면 진공)

▣ 압력의 단위

  1[atm] = 10.332 [mH2O] = 760 [㎜Hg] = 101,325 [Pa] =101.325 [kPa]  = 0.101325 [MPa]

​

ex1. 국소대기압이 98.6 [kPa]인 곳에서 펌프에 의하여 흡입되는 물의 압력을 진공계로 측정하였다. 진공계가 7.3 [kPa]을

         가리켰을 때 절대압력은 ?

  ⊙ 절대압력 = 국소 대기압 + 계기압력

      ∴ Pabs = 98.6 [kPa] - 7.3 [kPa] = 91.3 [kPa]

      ※ 진공계의 값은 (-)의 압력을 측정하는 것이다. 그러므로 압력을 빼주게 된다.

ex2. 소방펌프차가 화재현장에 출동하여 그곳에 설치되어 있는 수조에서 물을 흡입하였다.

        이 때 펌프 입구의 진공계가 60 [kPa]을 표시하였다면 손실을 무시할 때 수면에서 펌프까지의 높이는 약 몇 [m]인가 ?

  ※ 단위 환산 : 1[atm] = 10.332 [mH2O] = 760 [㎜Hg] = 101.325 [KPa]​

     ⊙ 측정값 × 대상값 / 기준값

​

라. 압력측정계기

  ▣ 액주계 : 액체의 기둥 높이를 기준으로 압력을 측정하는 방법 (液 : 진액, 柱 : 기둥주 計 : 셈할 계)을 말한다.

                     흔히 쓰이는 액주계에는 다음과 같다.

   ⊙ 피에조미터관 (Piezometer)

   ⊙ U자관 액주계 (U-tube Manometer1)

   ⊙ U자관 차압 액주계 (U-tube Manometer2)

   ⊙ 경사관 차압 액주계 (Inclined - tube Manometer)

【 피에조미터관 】

  ⊙ 한쪽 끝이 개방되어 있는 수직관이 압력을 측정하고자 하는 용기 A에 부착되어 있는 액주계를 '피에조미터관'이라고

       한다.

측정방법은​

【 U자관 액주계 (U-tube Manometer1) 】

 ⊙ 피에조미터관의 단점을 보완하기 위한 것으로 U자관 액주계이다. 용기 A에 있는 유체

     와 다른 유체를 액주계에 사용한다. 이 유체를 "계기 유체 (Gage Fluid)라고 한다.

측정방법은​

【 U자관 차압 액주계 (U-tube Manometer2) 】

  ⊙ U자관 차압 액주계를 이용하여 두 용기간 압력차이를 쉽게 구할 수 있다.

측정방법은​

【 경사판 차압 액주계 (Inclined-tube Manometer) 】

⊙ 두 용기 사이의 압력이 아주 미세한 경우에는 경사관 차압 액주계를 사용한다.

측정방법은​

ex1. 다음 경사 수압관에서 θ = 30 ˚, ℓ=10 [㎝], 비중 1.2 일 때의 압력 PA 를 구하여라.

ex2. 다음의 역 U자관 Manometer에서의 압력차 Px -Py 는 ?

압력차는​

마. 수중 평면에 작용하는 정수압

 ▣ 압력은 수심에 따라 선형적으로 분포하고 압력은 수심에 따라 비례한다.

   ① 전수압 F = γ · h · A

   ② 수압의 중심 : 평면의 도심

      ※ 전수압이 작용하는 위치는 도심 또는 무게 중심에 작용한다.

​

▣ 연직면에 작용하는 압력

  ① 전수압 ( P = F )

  ② 수압의 중심 hp​

▣ x축에 관한 2차 모멘트

  ⊙ 사각형

#정수압 #액주계 #마노미터 #Manometer #U자관 #피에조미터관 #절대압력

#계기압력 #대기압 #파스칼 #수압기

일과 열은 유사점이 많다는 것을 알게 되었다.

보호의 규약을 예를 들면 시스템으로 전달되는 열은 +Q, 즉, 시스템에 외부로 부터 가해지는 에너지를 나타내며, 시스템이 하는 일은 +W, 즉, 시스템에서 외부로 보내지는 일 에너지를 나타낸다.

위 그림과 같이 기체가 들어 잇는 실린더에 움직이는 피스톤이 끼워져 있는 상태에서 열과 일에 대하여 살펴보면 분명하게 알 수 있다. 경계내의 계인 기체에 열이 가해지면 온도가 증가하고 따라서 기체의 압력도 증가할 것이다. 이 때 압력은 이동계의 외력 Fext 에 의하여 그 크기가 다르게 나타난다. 만약, 압력이 일정하게 유지된다면 체적은 대신 증가해야만 한다. 열이 계로 부터 경계를 통해 외부로 전달되면 반대로 기체의 압력이 감소할 것이며 압력을 일정하게 유지하다고 하면 기체의 체적은 줄어들어야만 할 것이다.

또한 계에 열이 가해지면서 동시에 외력 Fext가 감소하는 경우는 기체의 압력이 감소되어 동시에 온도가 낮아질 것이다. 이와 같이 온도 변화의 방향이 서로 반대인 경우 두가지 효과가 작용함을 알 수 있다.

위 적분을 수행하기 위해서는 시간에 따른 각 순간 전달률 Q와 W의 변화를 알아야 한다. 전달률이 크게 변화하지 않는 시간동안에는 전달률은 단순 평균값을 사용하여도 된다. 즉,​

  ※ 팽창일 : P-V 선도의 면적​

ex2 : 밀폐용기에 비내부에너지가 200[kJ/㎏]인 기체 0.5 [㎏]이 있다. 이 기체를 용량이 500[W]인 전기가열로 2분 동안

         가열하였다면 최종 상태에서 기체의 내부 에너지는?  (단, 열량은 기체로만 전달된다고 한다.)​

ex 3 : 30 [℃]에서 비체적이 0.001 [㎥/kg]인 물을 100[kPa]의 압력에서 800 [kPa]의 압력으로 압축한다. 비체적이 일정하다

             고 할 때, 이 펌프가 하는 일 [J/kg]을 구하면 ?​

ex 4. 내부에너지 130 [kJ]를 보유하는 물질에 열을 가했더니 내부에너지가 200[kJ]로 증가했다. 이 물질이 외부에

           7,000[N·m]의 일을 하였을 때 가해진 열량은 몇 [kJ]인가 ?​

ex 5. 실린더 내의 밀폐된 가스를 피스톤으로 압축하는 과정에 13.32 [kJ]의 열을 방출하였고, 압축일의 크기는

         22,000 [N·m]이다. 이 가스의 내부에너지 증가량을 구하라.​

#일 #열 #에너지 #압축열 #온도 #시스템 #경계현상 #과도현상 #미분 #적분 #전달률 #평균값

1. 표면 장력

가. 응집력 : 같은 물질간에 서로 당기는 힘

나. 부착력 : 서로 다른 물질간에 당기는 힘

위 그림에서 물(H2O)은 산소 O와 수소(H2)가 편향적으로 결합되어 약한 자석의 성질을 띠게 된다. 이렇게 자석의 성질에 의하여 일반적으로 같은 분자간 또는 서로 다른 분자간에 인력이 작용하게 된다. 그런데 물은 부착력이 응집력 보다 크고 수은은 응집력이 부착력 보다 크다. 따라서 위 그림과 같이 물과 수은을 유리 판위에 놓으면 물은 퍼져서 반타원형 모양이 되고 수은은 거의 원형 모양을 유지하게 된다. 또한 가느다란 유리관에 두 물질을 넣으면 물을 대기면 보다 높게 올라가게 되고 수은은 내려가게 된다. 이는 부착력과 응집력 그리고 두 물질의 비중량의 영향을 받아 나타나는 현상이다.

이 때 물기둥이 멈췄다는 것은 위로 끌어 올리는 힘과 아래로 내리는 힘이 평형을 이루었다고 할 수 있다. 따라서 물은 표면장력은 유리관 전체에 작용하게 되므로 물의 전단응력에 원주 둘레의 길이를 곱한 값이 되며 이 때 전단응력 방향으로 힘을 적용해야 하므로 cos θ 값을 곱해 주게 된다. 그런데 이 전단응력은 높이 올라간 물기둥의 중력과 같게 되므로 유리관의 단면적에 높이 곱하고 이에 비중량을 곱한 값과 같게 된다. 이를 식으로 나타내면 다음과 같다.​

ex : 1[㎜] 간격을 가진 2개의 평행평판 사이에 물이 채워져 있는데 아래 평판을 고정시키고 위 평판을 1 [m/s]의 속도로

        움직였다. 평판 사이의 물의 속도분포는 직선적이고 물의 동점성계수가 0.804 ×10-6 [㎡/S] 일 때 평판의 단위 면적에

         걸리는 전단력은 약 [N]인가 ?

ex : 안지름 1[㎜]의 모세관을 표면장력 0.075 [N/m]의 물 속에 세울 때 물이 올라가는 높이는 약 몇 [㎜]인가 ?​

2. 유체의 압축성

▣ 체적탄성 계수 : 체적탄성계수는 부피의 감소율 분의 압력 변화률로 나타낸다.​​

3. 흐름의 분류

가. 레이놀즈(Reynolds) 수

※ 레이놀즈의 수에 따라 유체의 흐름을 층류, 천이영역, 난류로 분류할 수 있다.​

  ▣ 층류 : Re ≤ 2,100

  ▣ 천이영역 : 2,100 ≤ Re < 4,000

  ▣ 난류 : Re ≥ 4,000

​

나. 흐름의 분류

▣ 정상류(Steady flow) : 유체의 흐름의 속도가 시간에 따라 변화하지 않고 일정한 흐름​

▣ 비정상류(Unsteady flow) : 유체의 흐름의 속도가 시간에 따라 변하는 흐름​

#표면장력 #응집력 #부착력 #압력 #응력 #속도 #분포력 #탄성계수 #압축률 #레이놀즈

#정상류 #유속 #유체

【 단위 】

우리나라는 미터계를 쓰고 있으나 영연방국가 들은 영국 단위계를 쓰는 곳도 있다.

 ▣ 미터계 (Metric unit system) : 우리나라

 ▣ 영국단위 계 (Britesh unit system)

  ⊙ 1 [m] = 3.2808 [ft]

  ⊙ g (중력가속도) = 9.8 [m/sec2) = 32.2 [ft/sec2]

​

【 힘 (무게) 】

▣ 마찰이나 저항이 없는 어떤 물체에 추가적인 속도를 내게 하는 원천으로 일반적으로 힘 = 질량 × 가속도 라고 표현한다.

   F = ma                            F : 힘

      = ㎏·㎝/sec2                m : 질량 [㎏]

      = ㎏ ·m/sec2                a : 가속도 (cf : g : 중력가속도)

      = N

    ∴ 1[N] = 1 [ ㎏ ·m/sec2 ] cf) 중량 [㎏f] : 1kg × g = 9.8 kg ·m/sec2

​

【 밀도, 비중량 (단위중량), 비중 】

  ▣ 밀도는 단위 체적당 질량을 말한다.

       여기서 단위라는 말은 "1" 을 의미하므로 일반적으로 미터단위계에서는 1[㎥] 당 질량을 말한다.

       이를 식으로 나타내면 다음과 같다. ​

  ▣ 비중 : 4 [℃] 물의 체적과 동일한 체적의 무게비를 말한다.​

   ⊙ 단위중량 (비중량) : 단위 체적당 무게 (무게 = 질량 × 중력가속도)

​

 ▣ 단위 중량 (비중량) : 단위 체적당 중량(무게)​

     cf : 물의 밀도 : 1,000 [㎏/㎥]

           물의 비중량 : 9,800 [N/㎥]

​

 ▣ 차원

  ⊙ 물리적인 관계를 나타내는 물리량은 기본량을 적당히 조합해서 지수의 꼴로 나타낼 수 있다. 이 때 물리량을 나타내는

       단위를 차원이라고 한다.

       일반적으로 물리량은 질량[M], 길이 [L], 시간[T]을 기본량으로 한 [MLT]계를 이용하여 표현할 수 있다.

  ex)  F = m·a = 질량 × 가속도 = 질량 × (거리/시간) / 시간

        [F] = [M] · [LT -2] = [MLT -2]​

  ex : 밀도를 [MLT] 차원으로 나타내면 ?

  단위에 대한 접두사​

 ex : 비중병의 무게가 비었을 때는 무게가 2N이고, 액체로 충만되어 있을 때는 8 [N] 이었다. 액체의 체적이 0.5 [ℓ] 이면

        이 액체의 비중량은 몇 [N/㎥] 인가 ?​

 ex) 압력과 에너지, 운동량의 차원은 ?

   cf : 압력 (P) = F/A, 에너지(일) = 힘 × 거리= F · L, 운동량 = 힘 × 시간 = F · T

    풀이 : 압력 = [MLT-2] / [L2] = [ML-1T-2]

              에너지 = [MLT-2] × [L] = [ML2T-2]

              운동량 = [MLT-2] × [T] = [MLT-1]

​

ex : 표면장력의 차원은 ?​

▣ 물의 점성

 ⊙ 물분자가 상대적인 운동을 할 때 물분자간 혹은 물분자와 고체 경계면 사이에 마찰력을 유발하는 물의 성질, 마찰력은

      전단응력이라고 하는데 이 전단응력으로 인하여 물체의 상판을 움직이면 유체가 따라 움직임의 정도가 깊이에 따라

      달라지게 된다. 따라서 전단응력의 변화율을 깊이의 변화율로 나눈 것이 전단응력이 되는데 이때의 비례상수를

      점성계수라고 한다.

   평판의 면적 : A

   평판의 단위 면적당 마찰력 : τ (전단응력)​

▣ 동점성 계수​

ex : 점성계수와 동점성계수의 차원은 ?

 ▣ 점성계수는 전단응력과 전단속도와 깊이와 비율과의 관계나타내 주는 상수를 말한다.​

▣ 동점성계수는 점성계수를 밀도로 나눈 값이다.​

#질량 #밀도 #차원 #점성계수 #동점성계수 #비중량 #비중 #전단력 #전단응력 #점성

#표면장력 #가속도

1. 사이클 과정과 열역학 제1법칙

​

밀폐계에서의 열역학 제1법칙에 대하여 알아 보자. 영국의 J. Watt가 소형 증기기관을 발명한 이후 , 여러 장치를 통하여 열에너지를 기계적 에너지로 바꿀 수 있음을 경험적으로 알고 있었으나 이의 실현을 위해서 열변환 장치를 통한 실험으로 부터 그에 대한 확증을 얻어 낼 수 있었다. 그 후 영국의 J. P. Joule은 아래 그림과 같은 간단한 장치를 통하여 열 상당량을 구할 수 있는 실험을 하였고 이것으로 부터 열의 관계를 양적으로 나타내었다.

"즉, 열과 일은 본질적으로 같으며 에너지의 일종으로 열은 일로 변환시킬 수 있고 또 반대로 일을 열로 변환시킬 수도 있다. 따라서 밀폐계가 임의의 사이클을 이룰 때 열전달의 총화는 이루어진 일의 총화와 같다" 라고 표현할 수 있다. 이것이 열역학 제1법칙 (The first law of thermodynamics)이라 하고 에너지 보존의 법칙 (Law of conservation of energy)이라고도 한다.

위 그림과 같은 줄의 실험을 통하여 열과 일의 양적관계를 구하면

일 (Work) = 힘(force) × x (힘을 받아 힘의 방향으로 이동한 거리)로 표시하고 공학 단위는 ㎏f·m 이다. 이 공학 단위에서 기계적인 일은 W[㎏f·m]가 열량 Q [kcal]로 바뀌고, 열량 Q [kcal]가 일량 W [㎏f·m]로 변환될 때, 다음 관계식이 성립한다.​

으로 나타낸다. 따라서 전 사이클에 대하여 위식의 적분값의 W = J Q [㎏f·m] 또는

Q = A W [kcal]가 되며, 다음 식으로 나타낼 수 있다.​

2. 계의 검사질량의 상태 변화에 대한 열역학 제1법칙

​

검사질량이 상태변화를 하는 과정에 대한 열역학 제1법칙에 대하여 살펴보자.

시스템이 위 그림과 같이 상태 1로 부터 상태 2로 과정 A에 따라 변화하고 상태 2 로 부터 1로 과정 B에 따라서 되돌아 가는 사이클을 겪는 계에서 열역학 제1법칙의 식을 다시 쓰면

다음과 같다.​

위의 그림과 같이 2개의 분리된 과정을 고려한다면 과정 A식과 과정 B식은 같으며 아래식과 같게 된다.​

가 되며 또 다른 경로는 계가 상태 1로 부터 상태 2로 과정 A를 따라 변하고 과정 C에 따라서 상태 1로 되돌아 가는 사이클을 생각하면 다음 식과 같게 된다. 즉,​

이 된다. 위 두식을 정리하면 다음과 같은 식이 된다.

위 식을 이항 정리하면 다음과 같다.​

이 때 경로 B와 C는 상태1과 2 사이의 임의의 과정을 표시하고 (δQ -δW)라는 양은 상태 1,2 사이의 모든 과정에 대하여 같게 된다. 따라서 (δQ -δW) 차이는 최초와 최종의 상태에만 좌우되며 둘 사이의 경로는 좌우되지 않는 함수이다. 이 차이를 다음과 같이 사이클 동안 에너지 변화에 대한 미분으로 쓰고 dE는 주어진 상태에서 시스템이 갖는 모든 에너지의 변화를 나타낸다.

    dE = δ Q - δ W

따라서 E (모든 에너지) = U(내부에너지) + KE(운동에너지) + PE (위치에너지)이다. 이들의 변화를 구성하는 모든 항들은 점할수 이므로

    dE = dU + d(KE) + d(PE)

의 미분식이 가능하며 내부 에너지 (dU), 운동에너지 (dKE), 위치에너지 (dPE)의 미분합으로 쓸 수 있다. 각 에너지 관계식을 적용하여 양변을 적분하면 다음 식이 된다.​

위 식들에 대해 몇가지 관찰해 보면, 첫째 계의 에너지를 표시하는 상태량 E가 존재한다는 것이 밝혀진 것이고, 상태변화에 대한 제1법칙만을 적용할 수 있다는 것이다. 둘째는 위 식은 사실상 에너지 보존에 관한 식이다. 즉, 계의 에너지 정미 변화는 항상 열과 일로써 계의 경계를 넘어서는 정미 에너지 전달과 같다. 셋째로 위 식들은 내부에너지, 운동에너지, 위치에너지의 변화만을 줄 수 있음을 관찰할 수 있다. 만약​

이라면 위 식은 다음과 같이 쓸 수 있다.​

또한 위 식을 단위 질량, 단위 중량당으로 쓰면 다음과 같다.​

위 두 식을 공학단위로 고쳐 쓰면​

A는 일의 열당량 값으로 1/427 [kcal/㎏f·m]이다. 만약 반대로 위 두 식을 미분식으로 다시 쓴다면 다음과 같다. 아래식을 열 역학 제1법칙에 대한 일반식이라고 한다.

다음은 에너지 E에 대하여 알아보자. 앞에서 E는 크게 내부에너지(U)와 위치에너지 (PE), 운동에너지 (KE)의 합으로 나타낼 수 있었다. 이 에너지는 일을 할 수 있는 능력을 말하며 일의 단위와 같고, 다음과 같이 설명할 수 있다. 즉, 내부 에너지는 한 계에 외부로 부터 열이나 일을 가할 때 그 계가 외부와 열의 수수없이 외부에 일을 하지 않는다면 이들 에너지는 그 계의 내부에 축적된다고 생각할 수 있다. 이와 같이 계의 내부에 저장된 에너지를 내부에너지(Internal energy)라고 하며, 보통 U[kJ] 또는 u [kJ/㎏]로 표시한다. 다시 말하면 내부에너지는 계의 총에너지에서 기계적 에너지를 뺀 나머지를 말하는 것으로 이 때 기계적 에너지(역학적 에너지)는 외부 에너지 (External energy)를 말한다. 따라서 에너지식은 다음과 같이 내부에너지와 외부에너지의 합으로 나타낼 수 있다.

      ∴ 총 에너지 (E) = 내부에너지 (IE) + 외부에너지 (EE)

또한 보통은 분자가 분자력에 의해서 서로 위치 에너지를 가지며 또한 운동에너지를 가진다. 이와같은 분자의 집단인 물질의 내부에 보유되는 에너지가 그 물질의 내부에너지가 된다. 따라서 물질의 내부 에너지는 분자의 현재의 집합상태와 운동에만 관련되기 때문에 물질의 과거의 상태와는 무관하고 물질의 현재 상태에 의해서만 정해지는 상태량이라고 할 수 있다. 그리고 내부 에너지에는 분자의 운동에너지로 온도를 상승시키는 잠열과 분자상호간의 힘에 저항하여 융해 또는 증발에 이용되는 잠열이 포함된다.

다음은 위치에너지와 운동에너지에 대하여 알아보자. 위치에너지(Potential energy)PE의 크기는 다음과 같다.

      PE = mg · Z [J]

      여기서 mg = W : 무게 [N], Z : 높이 [m]이다.

또한 운동에너지 (kinetic energy) KE의 크기는 다음과 같이 나타낸다.​

여기서, m : 질량 [㎏], V : 물질의 속도 [m/sec]

​

#열역학 #열역학제1법칙 #에너지보존법칙 #열당량 #일당량 #운동에너지 #내부에너지 #위치에너지 #에너지 #경로함수 #시스템 #일 #힘 #사이클 #와트