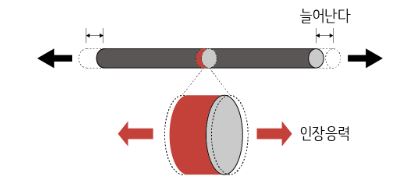
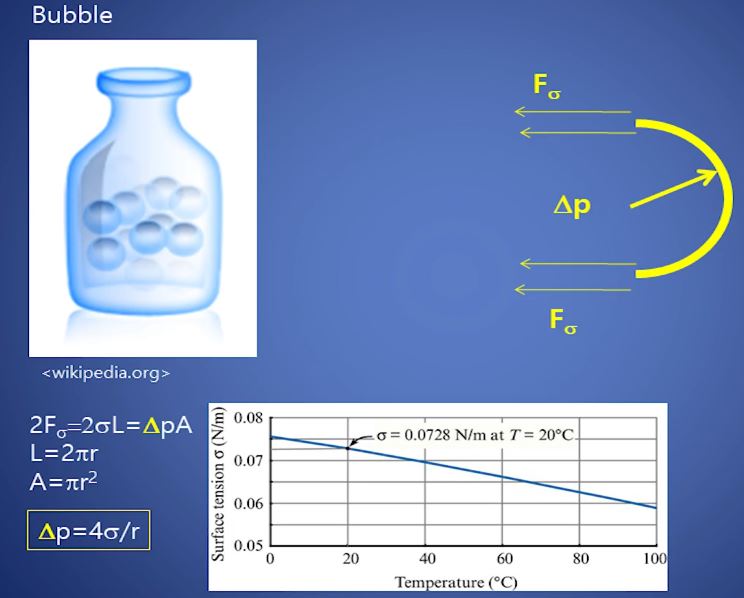
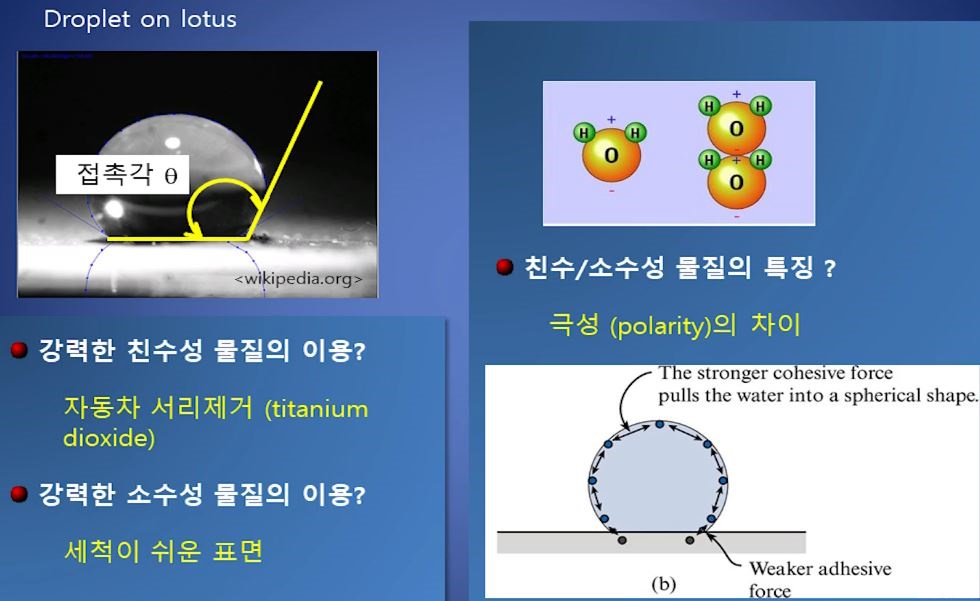
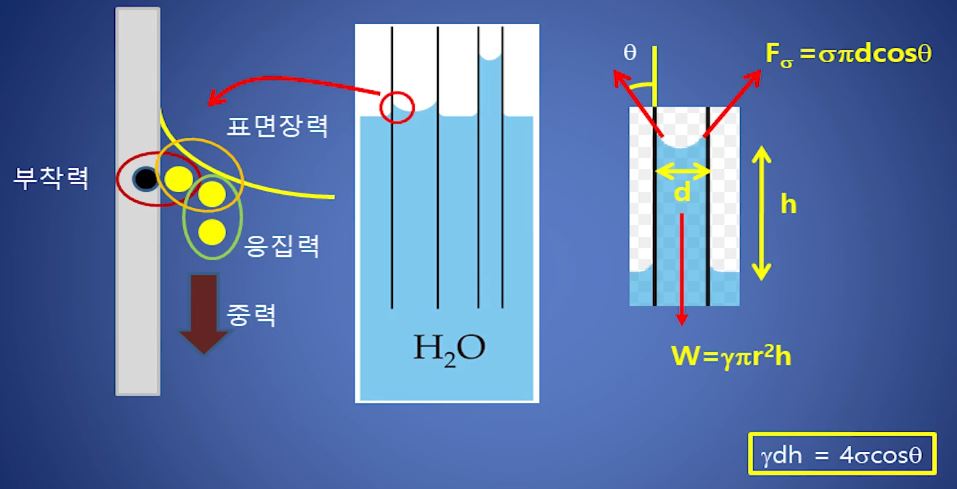
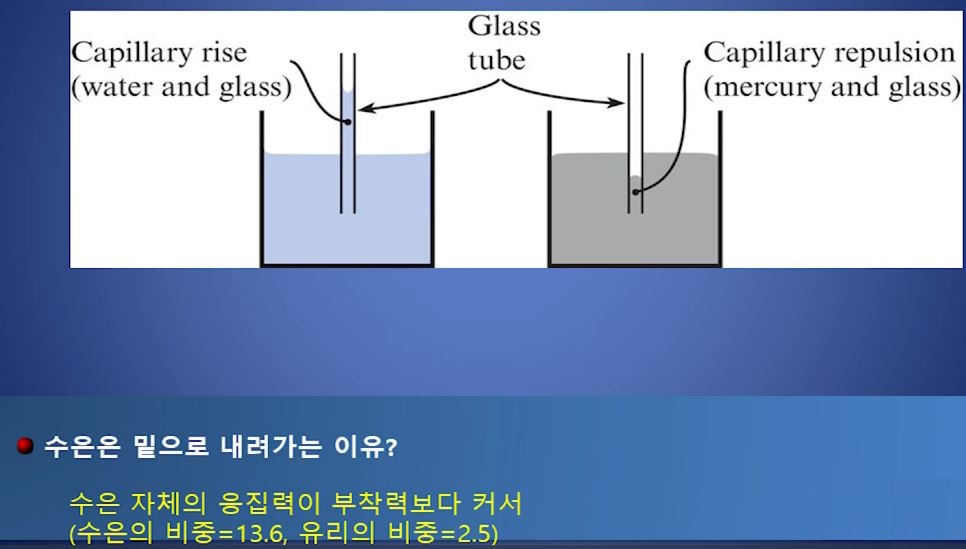
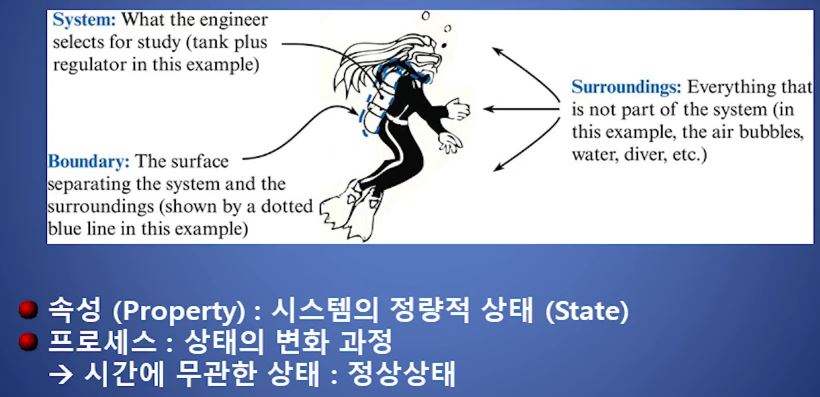
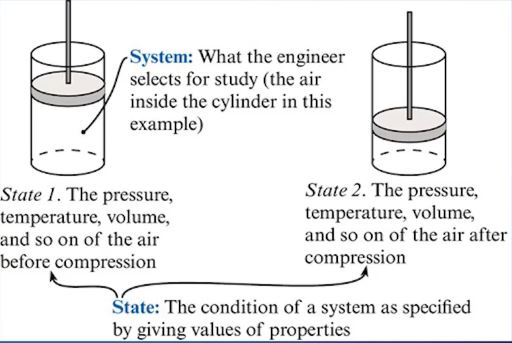
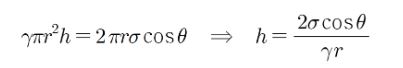▣ 점성은 유체 (액체, 기체)가 가지고 있는 중요한 특성으로 물질의 분자간의 서로 끌어 당
기는 힘에 의해 발현되기도 하고 분자간의 충돌에 의하여 발현되기도 한다. 점성은 유
체의 아주 독특한 특성이고 유체의 흐름에 영향을 주는 중요한 인자이다.
1. 점성 유체

유체는 이상유체와 점성유체로 나뉜다. 그런데 모든 유체는 끈적임을 가지고 있어 모든 유체는 점성유체라고 할 수 있다. 반면에 이상 유체는 유체의 물리적 현상을 파악하기 위해
가정한 유체이다. 점성 유체는 Newtonian Fluid와 (Non- Newtonian) Plastic Fluid
로 나눌 수 있다.
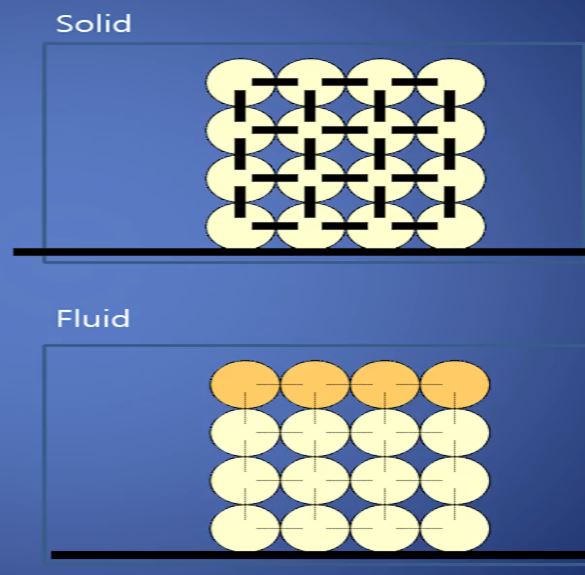
위 그림 오른쪽은 유체를 나타내는데 물, 시럽, 꿀, 버터, 실리콘 등은 유체이다. 유체와
고체를 구분하는 것은 외력을 가한 후 회복하였을 때 원래 상태로 복귀하는 것을 고체라
하고 되돌아 오지 않는 것을 유체라고 한다. 유체는 원래대로 회복되지 않고 일정시간 동안
흐름을 유지하게 된다.
가. Newtonian Fluid

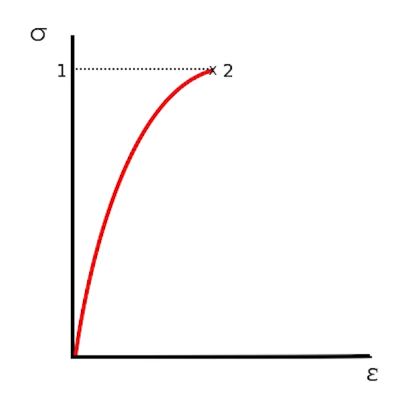
위 그림 왼쪽은 Newtonian Fluid 특성을 나타내는 그래프이다. 그래프에서 Y축의 Stress
는 단위 면적당 힘을 말하고 x축은 변형율을 나타낸다. 변형률은 어떤 물체에 물리적인 힘
이 가해져서 당초 물체 대비 변형된 물체의 크기를 말한다. 고체의 경우에는 항복점까지는
작용하는 힘에 대하여 변형률이 비례하다가 항복점이 지나면 급격히 커지고 Failure 지점
에서는 고체가 파괴된다. 항복점 까지는 힘과 변형률이 선형관계인 탄성상태라고 한다.
Newtonian Fluid는 전체 곡선이 선형상태이고 탄성상태를 보인다.

먼저 고체에 대하여 알아보자.
위 그림의 왼쪽을 보면 당초 정4각형의 물체에 전단력이 가해져서 평형사변형으로 변형된
것을 볼 수 있다. 바닥은 고정되어 있고 위면만 변형되어 있다고 할 때 변형된 크기를 dx라
하고 변형각을 γ이라고 하면 재료역학의 고체변형율에서 위와 같은 식이 성립하게 된다.
나. 점성유체 (Viscous Fluid)
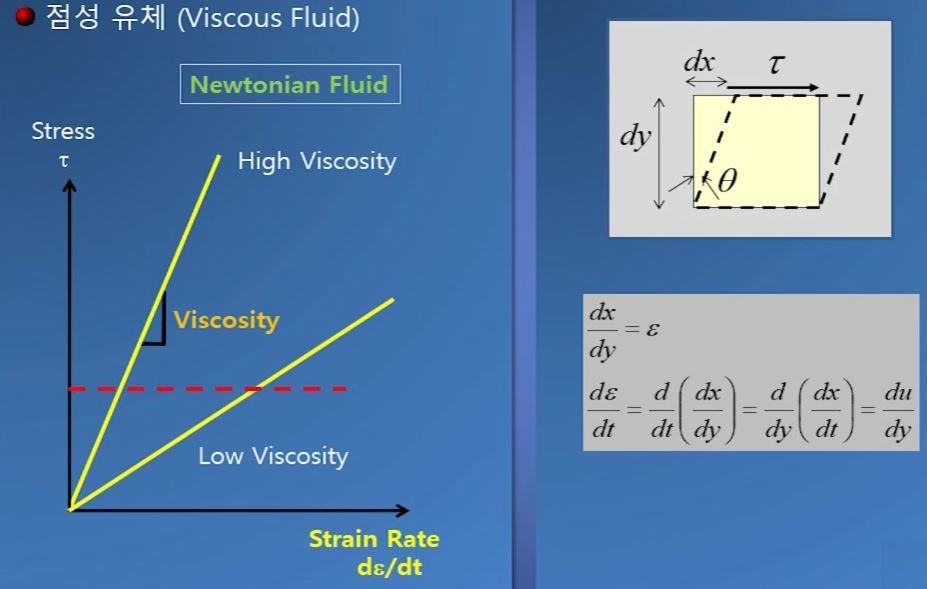
유체의 경우에는 x축이 변형율의 변화율 즉, 변형율이 시간에 따라 어떻게 변화하는지를
나타낸다. 이 때 2개의 특성곡선이 나타나는데 하나는 High Viscosity이고 다른 하나는
Low Viscosity 이다. 유체는 전단응력이 가해지면 변형이 발생하고 전단응력이 제거되어
도 일정시간동안 흐름이 지속된다. 위 그림 오른쪽을 보면 정4각형 모양의 유체를 가정했
을 때 아래면은 고정되어 있고 위 쪽에 전단응력을 가해 평행사변형으로 변형되었다고
하자. 변형률은 ε = dx/dy 이다. 정4각형이므로 x = y 이기 때문이다. 이 때 변형률을 시간
으로 미분을 하면
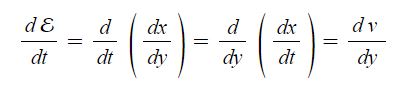
위 식에서 ε = dx/dy이므로 이식을 dt, dy 를 자리를 바꾸어 변형을 하면 dx/dt가 나오는데 이는 거리를 시간으로
미분한 것이므로 속도가 된다.
결국 변형률의 미분 즉, 변형률의 변화율은 y축 즉, 두께에 대한 속도의 변화율로 함수 관계가 변화하게 된다.
이는 어떤 전단력을 가했을 때 같은 물질이라도 두께에 따라 변형률의 크기가 달라지는 것을 의미한다.
따라서 액체에 있어서는 고체와 달리 변형률만으로 점성계수를 삼을 수 없다. 이로 인하여 변형률을 미분하여
변형률의 변화율과 전단력과의 관계를 점성계수로 삼은 것 같다.
왼쪽 그림은 점성이 크면 같은 응력이 주어졌을 때 변형률 변화가 크지 않고 점성이 낮은 경우에는
변형률이 크다는 것을 보여준다. 따라서 같은 힘을 주었을 때 점성이 낮은 유체가 잘 흘러가게 된다.
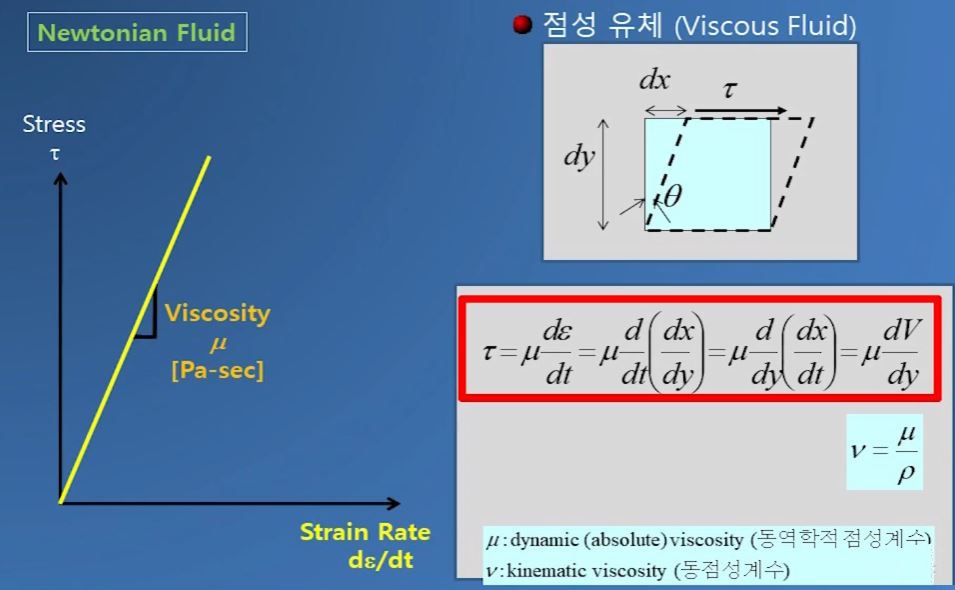
그런데 물질마다 변형률의 변화율과 전단력과의 관계가 다르게 나타나는데 선형으로 나타는 유체를
Newtonian 유체라고 한다. 이들 유체에서는 전단력은 변형률의 변화율과 선형관계에 있기 때문에 특정 상수로
전단력과 변형률의 변화율과의 관계를 나타낼 수 있다.
이와같이 주어진 전단응력과 변형률의 변화율의 관계 그래프에서 직선의 기울기를 점성 (Viscosity)라고 부른다.
기호로는 μ를 사용한다. 점성의 단위는 [Pa-sec]을 쓴다.
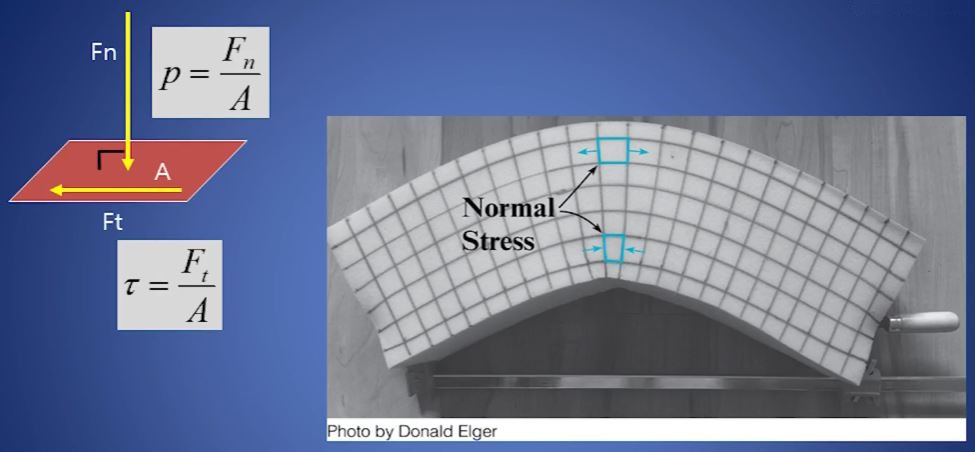
전단응력 τ 은 점성계수 μ 와 두께 (y축)에 대한 변형률의 변화율을 곱한 값이라 할 수 있다.
이것을 정리하면 전단응력 τ = μ (dV / dy)이 된다.
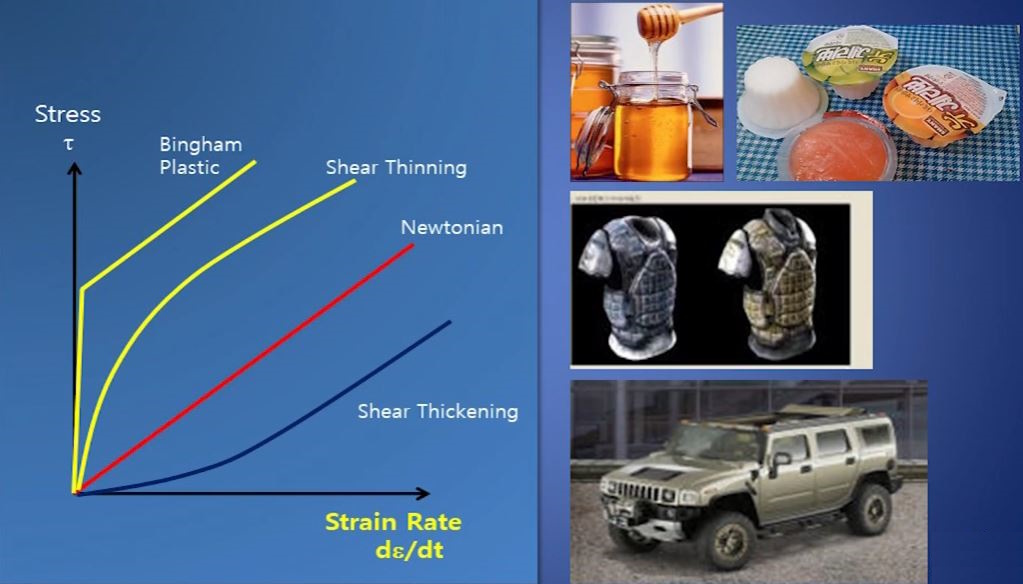
위 그림은 물질의 변형률의 변화율에 대한 전단응력의 관계를 나타나는데 Newtonian
Fluid 는 이들 관계가 직선형태 즉, 기울기가 일정한 비례관계에 있다.
위 그래프에서 Shear Thing의 경우에는 처음 힘을 가하면 변형률이 크지 않은데 일정한
힘을 넘어서면 유체가 잘 흐르는 것을 보여주는데 우리 주변에서 용기에 들어 있는 케찹을
생각하면 이해하기 쉽다. 케찹이 처음에는 잘 나오지 않다가 한번 나오기 시작하면 잘 나오
게 된다. 반대로 Shear Thickening의 경우에는 전단응력이 작을 때는 잘 흐르다가 응력이
커지면 잘 흐르지 않는 경우이다. 이런 경우는 물체에 힘을 가하면 딱딱해지는 특성을 갖는
물체에서 나타나는 특성이다.
왜 이런 특성들이 나타날까 ?
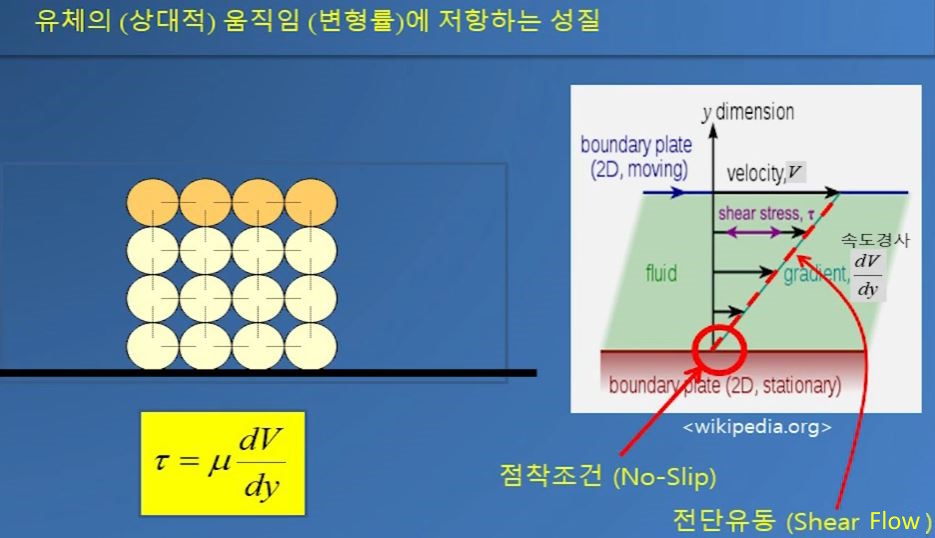
점성이란 응력과 변형률의 시간적 변화에 대한 관계를 나타내 주는 특성곡선의 기울기라고
했다. 점성이란 물체의 움직임에 저항하는 성질이다. 저항하는 힘이 큰 물질은 고점성 물질
이라 하고 작은 물질은 저점성 물질이라고 한다.
위 그림처럼 유체의 맨 위층에 힘을 가하면 위층은 움직이려 한다. 맨 아래층은 고체 표면에
부착되어 있어 고체와 액체의 부착력이 크므로 흘러가지 않는다.
위 그림 왼쪽을 보면 위쪽은 변형률이 많고 아래쪽은 변형률이 작다. 이와 같이 Y축 방향에
따라 변형률이 달라지는 것을 볼 수 있다.

유체의 점성에 의해서 많은 특성들이 나타나는데 그 중의 하나가 경계층이다. 위 그림 왼쪽
은 어떤 고체 μ(y) 앞으로 일정한 속도로 μo 유체가 다가온다고 가정하자. 이 유체의 맨 아래
부분은 고체에 부딪히게 되는데 고체와의 부착력에 의해서 움직이지 않게 되고 위쪽으로
갈 수록 유체는 많이 흘러가게 되어 경계층을 이루는 모습을 보여 준다.
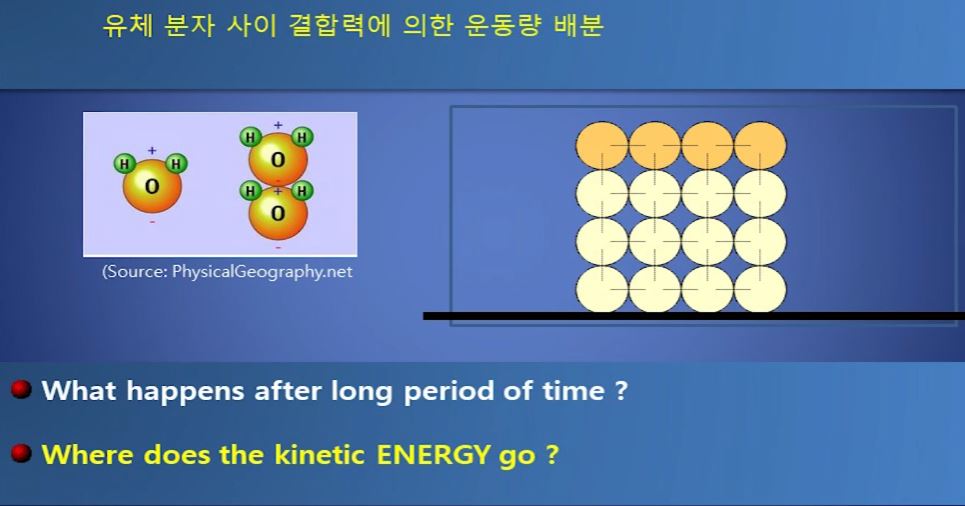
그러면 점성이 왜 발생하는 것일까 ?
위 그림 왼쪽은 물분자를 나타내 준다. 물 분자는 수소 2개와 산소 1개가 결합되어 있는데
수소가 편향되어 있어 마치 자석과 같은 특성을 나타낸다. 점성의 원인은 분자간의 결합력
때문에 발생한다. 오른쪽을 보면 위쪽 물분자에 힘을 가하면 만양에 물분자간에 결합력이
없다면 맨위층 4개만 움직일 것이다. 하지만 물분자간 결합력에 의해 이동하는 분자를 다른
분자들이 장아 당기게 되어 층층간의 분자들에 영향을 주게 된다.
점성은 분자간의 결합력에 의한 운동량의 배분으로 발생한다. 그러면 어디까지 이동할까?
힘에 의해 물이 유동을 하면 분자간에 마찰이 생길 것이고 이 마찰에 의해 운동에너지가
열에너지로 변형이 발생하고 발생된 열에너지는 공기중으로 전달되어 운동에너지가 열에너지로 소모가 된다.
이에 따라 운동에너지가 전부 열에너지로 소모될 때까지 이동하게 된다.
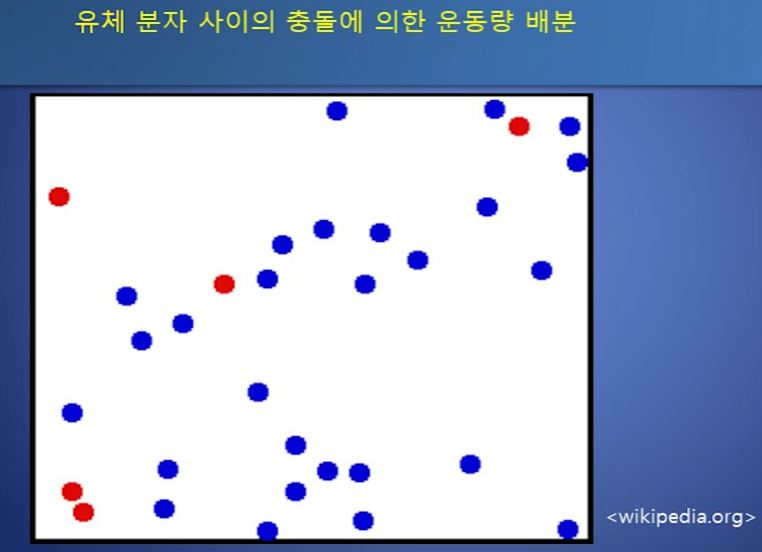
점성이 나타나는 두번째 원인은 분자간의 충돌에 의해 발생한다. 기체의 경우에는 공기분자
가 충돌하여 운동에너지가 배분되어 점성이 발생한다.

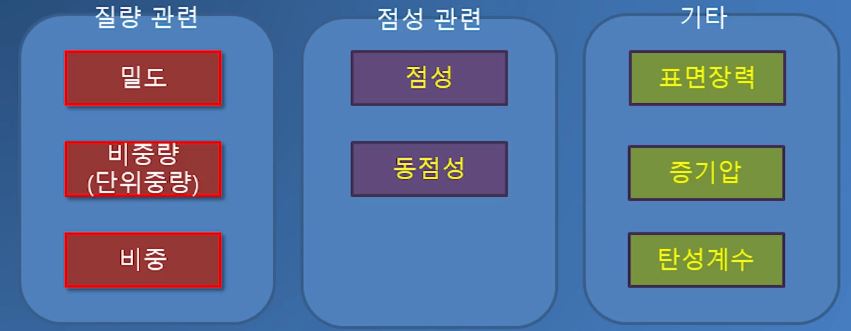
위 그림은 액체와 기체간 점성계수를 비교해 보았다.
위 그림에서 같은 액체라도 바닷물이 순수한 물보다 점도가 높은 것을 알 수 있다.
기체의 경우에도 물질의 종류에 따라 점도가 달라지는 것을 볼 수 있다.
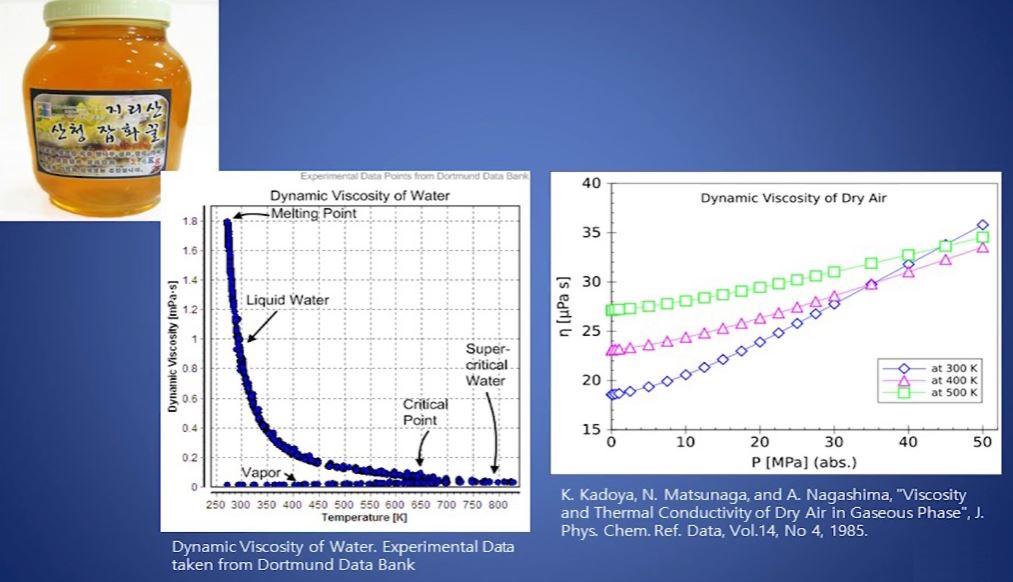
액체는 온도가 올라가면 점성계수는 낮아지는 반비례관계에 있다.
반면 기체은 온도가 올라가면 분자의 운동이 활발해져서 입자간에 충돌이 발생하여 점성계
수가 높아지는 비례관계에 있다.
2. 점성방정식
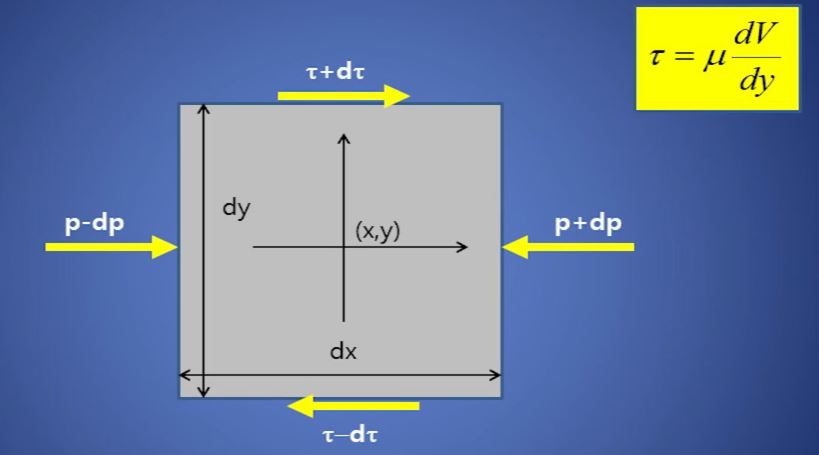
모든 유체는 점성을 가지고 있다.
점성에 의해 유체의 흐름이 달라지게 되는데 이에 대하여 알아 보자.
위 그림은 정4각형 dx, dy 크기의 유체입자가 있다고 가정하고 Y축과 수직으로 압력이
가해지고 위 아래면에는 전단력이 가해진다고 하자.
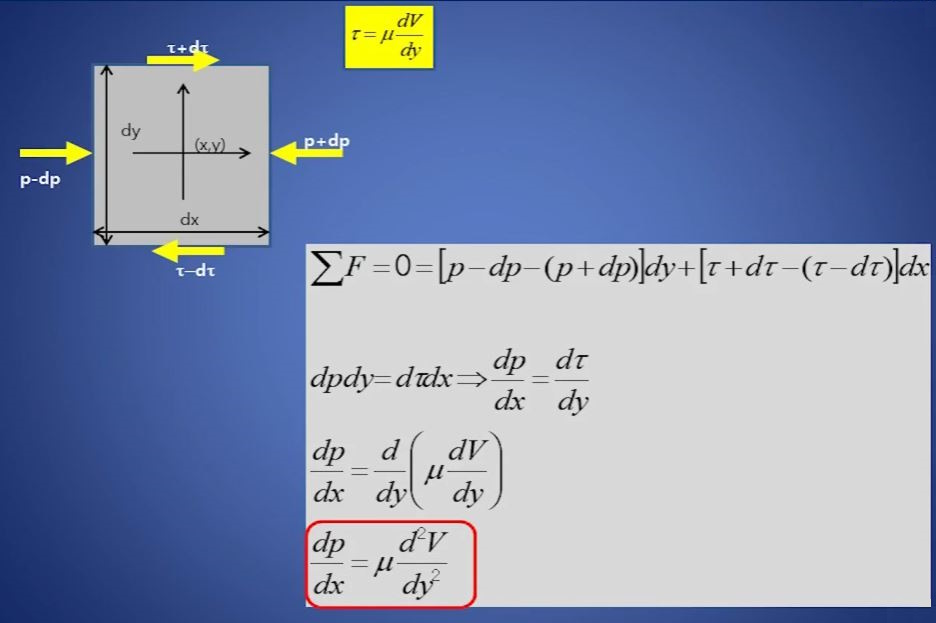
어떤 유체입자에 가해지는 힘의 평형이 이루어졌다고 하자. 예를 들면 x축 방향의 힘이
평형을 이루었다고 하면 x축에 가해지는 힘을 모두 더하면 "0"이 되겠다.
힘이 "0"이라는 식을 정리하면 위와 같은 식이 도출된다.
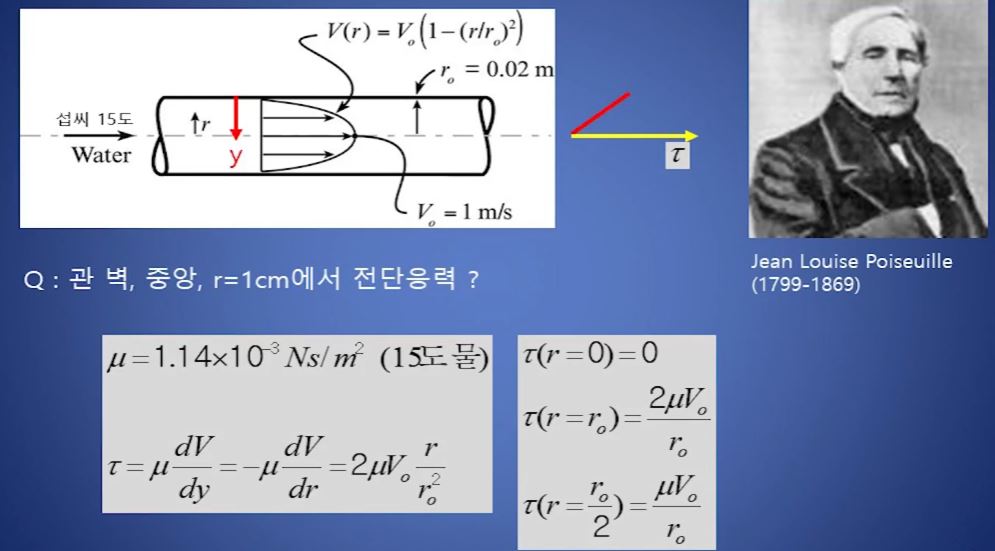
이와 같은 점성방식에 의해 예제를 풀어 보자.
위 식에서 점성은 관의 직경에 비례함을 알 수 있다.
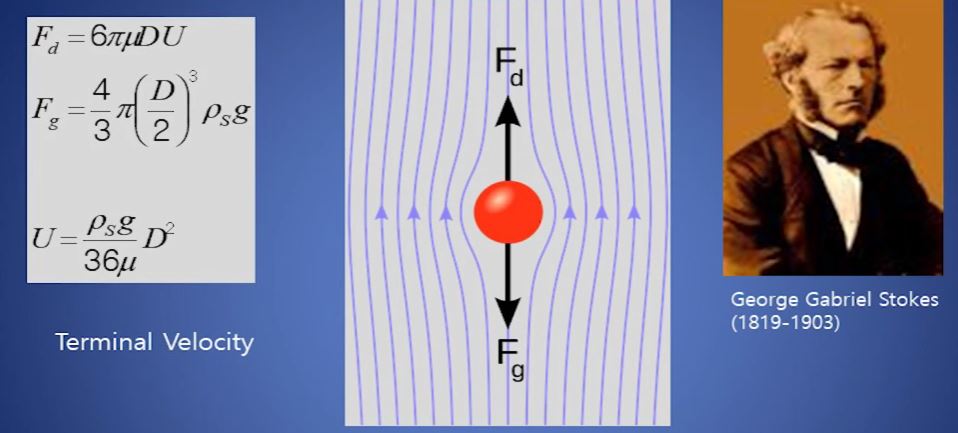
위 그림은 스토크의 원리에 대해 말하고 있다.
위 그림에서 보면 빨간색 물체에 그 주위로 유체가 흐르고 있는 것을 보여준다.
유체 역학중에서 매우 중요한 원리이다.
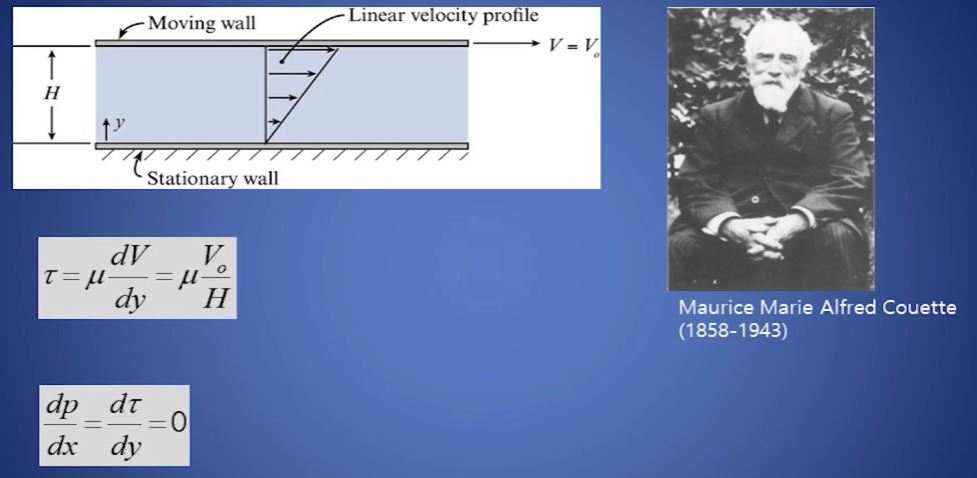
위 그림은 정착되어 있는 유체의 표면에 판넬을 올려 놓고 움직이는 실험이다.
위 쪽으로 갈 수록 유체의 움직임이 커짐을 알 수 있다.
이때 물 흐름의 변화율이 일정하고 압력차가 발생하지 않는다.
#유체 #점성 #점성방정식 #점성유체 #이상유체 #Newtonian #항복점 #탄성계수
#고체 #액체 #기체 #응집력 #부착력 #응력 #저항력 #전단응력
'소방설비기사 (기계) > 소방유체역학' 카테고리의 다른 글
| 압력이란 무엇인가 ? 뉴턴, 파스칼 그리고 토리첼리 (0) | 2023.08.14 |
|---|---|
| 정수압과 파스칼의 원리 : 유체 정역학 (0) | 2023.08.11 |
| 응력 (Stress)이란 무엇인가 ? 유체 역학 (0) | 2023.08.09 |
| 유체의 성질 (증기압, 비등, 비열, 압력, 전단응력) (0) | 2023.08.08 |
| 표면장력 (Surface tension), 모세관 현상 (Capillary action), 접촉각 (Contact angle) (0) | 2023.08.07 |
비버리님의
글이 좋았다면 응원을 보내주세요!