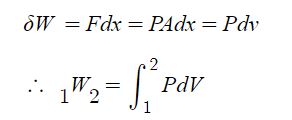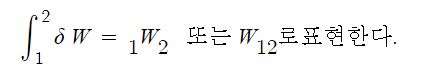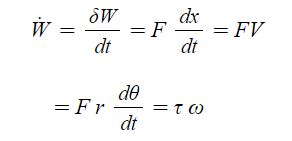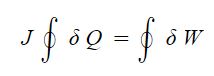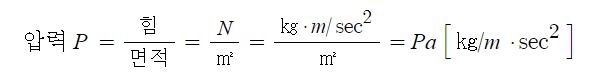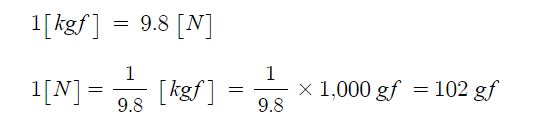1. 열의 정의
열에 대한 정의는 열역학에서는 일상적인 정의와는 다르다. 즉, 열은 물질 입자들의 운동의 결과로써 열크기의 척도는 온도이다. 이러한 열은 보다 높은 온도의 계로 부터 낮은 온도의 계로 전달되는 에너지의 한 형태를 말한다. 그러므로 열은 주어진 온도에 있는 계의 경계를 통하여 보다 온도가 낮은 계로 온도차에 의해 이동하는 경계현상이다. 다시 말하면 열은 경계를 넘어 설 때만 구별할 수 있다. 그러므로 열은 일시적이고 과도적이라 말할 수 있다.
열은 이와같이 계로 또는 계로 부터 전달되는 에너지로 정의 될 수 있는데 열의 단위와 일의 단위는 SI 단위계에서는 같다고 할 수 있다. 즉 SI 단위계에서는 열단위도 일 단위와 마찬가지로 Joule [J]이다.
그리고 열의 부호규약에 있어서, 계로 전달되는 열은 양 (+, Positive)으로, 계로 부터 빠져 나가는 열은 음(-, Negative)으로 정하여 사용하기로 한다. 문자기호는 열의 전체의 양은 Q[J]로 단위질량 당 열 [J/㎏]로 표시하여 사용된다. 열의 적분은 일과 같이 경로함수이고 불완전 미문에 대한 적분이며

위 식에서 Q12는 상태1과 2 사이에 주어진 상태 변화과정 동안 전달된 열의 크기이며, 단위시간당 시스템으로 전달되는 열의 양은 Q로 표시된다. 또한 계의 단위질량당 열전달 q [J/㎏]를 이용한다. 이 때 이 q 를 비열(Specific heat transfer)이라고 부르며 다음과 같은 식이 성립한다.

2. 열전달 방식의 대표적인 예
열전달은 에너지 이동의 한 방식으로 서로 다른 물질의 온도차에 의해 이루어진다. 물질분자는 병진(Translational), 회전 (Rotational), 그리고 진동 (Vibrational) 에너지를 가진다. 이러한 형태의 에너지는 상호작용(충돌) 또는 평균적으로 더 많은 에너지(보다 높은 온도)를 소유하는 분자들과 더 적은 에너지 (보다 낮은 온도)를 소유하는 분자들의 교환에 의해 주변의 분자에게 전달될 수 있고, 온도차와 그 물질의 전달특성에 따라 크기는 달라진다.
이러한 분자 상호간의 에너지 교환의 대표적인 것으로 전도, 대류, 복사가 있다.

전도(Conduction)의 열전달 방식은 온도가 서로 다른 고체와 고체, 그리고 고체와 유동하지 않는 유체 사이의 열전달 현상으로, Fourier 열전도 법칙으로 표현하면 열전달률 Q는 다음식과 같고 그 크기에 있어서는 열전도율(Thermal conductivity) k, 열전달면적 (heat transfer area) A, 온도구배 (Temperature gradient) dT/dx에 비례한다.

위 식에서 (-) 부호는 열전달이 높은 온도에서 낮은 온도로 전달된다는 것을 의미한다. 열전도율 k의 값은 상온 (300k)에서 순철 80.2 [W/m·K) 정도의 크기를 갖고 비금속 고체인 유리나 열음 또는 암석의 경우 1~10 [W/m·K) 정도 크기이며, 단열재는 비교적 낮아 대략 0.1 [W/m·K] , 기체의 경우 0.1 ~ 0.01 [W/m·K] 미만의 크기이다.
또 다른 열전달 ㅂ아식으로는 온도가 서로 다른 매체가 유동하는 유체와 유체, 유동하는 유체와 고체 사이의 열전달방식의 대류(Convection)가 있다. 즉, 특정 에너지값을 가진 유동유체가 다른 고체 표면의 위 또는 주위를 흐르게 될 때 전도에 의한 열전달 보다 두 물질을 접속시키거나 가깝게 만드는 유동이 더 지배적일 때 이러한 열 전달현상을 대류 열전달이라고 한다. 대표적인 예로 건물 주위에 부는 바람이나, 방열기(Radiator) 주위로 흐르는 공기, 관(Piping) 내부에 흐르는 물과 같은 유체 등의 열 교환기 (Heat exchanger)를 생각할 수 있다. 이 때 대류에 의한 총 열전달률 Q는 일반적으로 Newton의 냉각법칙을 따라 다음식으로 나타낸다.

위 식에서 열전달 특성은 대류 열전달계수 (heat transfer coefficient) h [W/㎡·K]가 포함되어 있는데 이 값은 유동하는 매체의 상태량, 유동현상, 물체의 기하학적 형상의 함수가 된다. 주어진 상황에 대해 열전달 계수를 계산하기 위해서는 전체 유동과 열전달 과정에 대한 상세한 역학적 요소들을 고려해야 함을 말해준다. 이 열전달 계수의 대표적인 값으로는 자연 대류의 기체 유동에서는 h = 2~25 [W/㎡·K] 정도이고 액체 유동에서는 h =50 ~ 1,000 [W/㎡·K] 정도이다. 강제 대류의 기체유동에서는 h = 25 ~ 250 [W/㎡·K]정도이고 액체유동에서는 h = 500 ~20,000 [W/㎡·K]이며, 증발과정의 상변화의 경우는 h = 2,500 ~ 100,000 [W/㎡·K] 정도이다.
마지막으로 열전달 방식의 하나로 열 복사 (Radiation)가 있다. 이 방식은 전·자기파 (Electron-magnetic wave)에 의한 에너지 전달방식이며, 중간에 어떠한 열전달 매체도 사용하지 않고 비어 있는 공간(진공)에서도 열 이동이 가능한 것으로 공업상으로 살펴보면 복사과정의 열방사(생산)와 열흡수(소비) 과정에는 물질의 존재가 필요하다. 이 때, 방사 또는 흡수하는 물체가 있을 경우 스테판-볼츠만 법칙 (Stefan-Boltzman law)에 의하여 완전한 흑체 표면으로 부터 방사량의 크기 Eb [W/㎡]는 다음 식과 같다.


#열 #에너지 #경계현상 #전도 #대류 #복사 #고체 #액체 #유체 #방사율 #복사체
#열복사 #방열기 #열교환기
'소방설비기사 (기계) > 소방유체역학' 카테고리의 다른 글
| 유체의 성질 : 단위와 차원 (0) | 2023.08.30 |
|---|---|
| 사이클 과정과 열역학 제1법칙 (0) | 2023.08.30 |
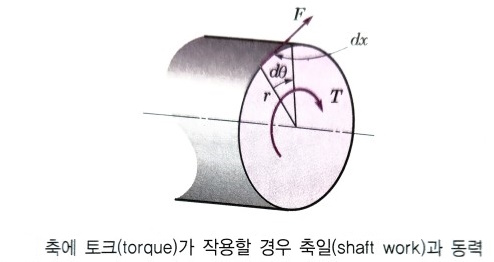
| 일의 정의와 단위 (0) | 2023.08.29 |
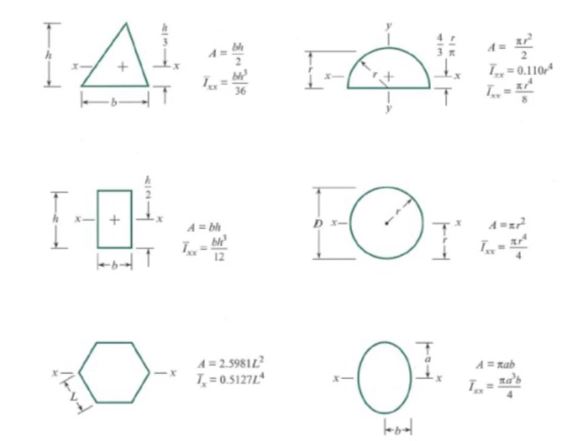
| 기하학 단면적 : 정수압방정식 (0) | 2023.08.24 |
| 정수압 방정식 (2) | 2023.08.21 |
비버리님의
글이 좋았다면 응원을 보내주세요!