1. 엔탈피(entahalpy)와 에너지식
상태 변화의 특별한 과정을 해석하다 보면 열역할 상태량의 몇 개가 합해져서 새로운 형태의 상태량으로 나타나는 경우가 있다.
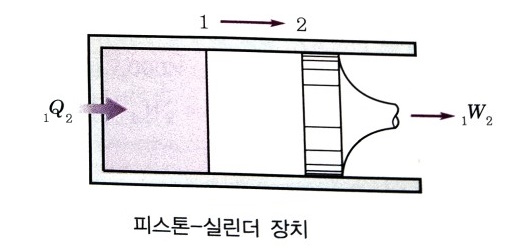
위 그림과 같이 검사질량에 대한 준평형 과정의 정압가열 과정의 경우를 살펴 보면 상태 1에서 상태 2로 팽창할 때 계에 대한 열역할 제1법칙 식을 적용할 때 다음과 같이 됨을 알 수 있다. 즉, 위치에너지와 운동에너지를 무시한다면 밀폐계의 열역학 제1법칙은 다음 식과 같다.
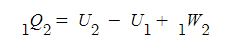
위 식에서 일의 변화는 상태1에서 상태2로 변화가 정압 과정이라면 다음과 같다.
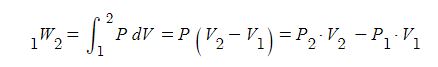
위 두식을 함께 정리하면 다음의 식이 성립된다.
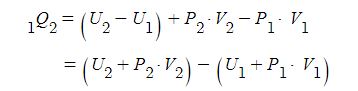
위 식에서와 같이 계가 정압과정 상태변화와 같은 특수한 경우에 대하여 새로운 형태의
U + PV (내부에너지와 운동에너지) 라는 양의 변화항을 얻을 수 있고 그것을 엔탈피(enthalpy) H라고 부른다.
이 엔탈피 (enthalpy)는 종량성 상태량이다. 결국 엔탈피란 열역학적 상태량을 나타내는 중요한 인자이며 내부 에저지 U와 유동과정의 에너지인 가역일 PV의 합이 된다.
따라서 엔탈피 H는
H = U + PV [kJ] 이고
단위 질량당의 엔탈피 h는 다음 식으로 표현할 수 있다.
h = u +Pv [kJ / ㎏]
단위 질량당 내부 에너지 처럼 단위 질량당 엔탈피 h를 비엔탈피(specific enthalpy)라고 하고 전체 질량의 엔탈피 H를 총엔탈피 (total enthalpy)라고 한다. 앞, 뒤 문맥에 따라 그 의미가 명백한 경우 두가지 모두를 엔탈피라고 하기도 한다. 여기서 u, P, v는 모두 어느 상태에 의하여 정해지는 상태량 값이며, h 역시 어느 상태에 의하여 정해지게 되는 상태함수이다. 따라서 엔탈피도 내부 에너지와 같이 상태변화 과정에는 관계없고 물질의 어느 상태에 따라 그 때의 물질의 상태량으로 결정된다.
즉, 엔탈피는 특별한 정압과정에서만 정의되는 값으로 전체 엔탈피 식을 아래 식과 같이 적용할 경우 정압과정에 대한 열량 변화와 엔탈피의 변화는 같음을 알 수 있다.
이번에는 에너지식을 다른 형태로 표현하는 일반식을 만들어 보자.
어느 물질이 외부에서 열량 δQ [kJ] 를 받아 내부에너지가 dU [kJ]가 증가하고, 외부에 δW [kJ]의 일을 하였다면 열역학 제1법칙에 의하여 다음과 같은 관계가 성립한다.
δ Q = d U + δ W
위 식은 어떠한 변화에도 성립되는 식이며 보통은 일반에너지식이라 부른다. 이 식을 적분을 하면 다음과 같다.
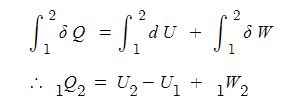
또한 물체 1[㎏]에 대한 비에너지식(specific energy)으로 다시 쓰면 다음과 같다.
δ q = d u + δ w
가역 과정의 경우 유동일은 w = P · v 가 되므로 위 식은 다음과 같이 다시 쓸 수 있다.
δ q = d u + d (P · v)
위 식의 미분과정을 다시 나타내면
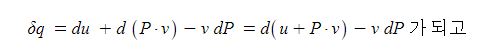
※ 열량의 변화는 내부에너지의 변화와 일량의 합으로 구해지는데 일량 중에서 정압상태에서 부피가 변하는 것은 기계일로
+(positive)이 이므로 더 해주고 동일한 체적으로 압력이 변화하는 것은 절대일로서 - (negative)이므로 빼주어야 한다.
이들 식으로 부터 일반 에너지식은 다음과 같이 나타낼 수 있다.
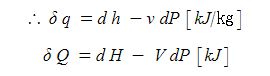
위식으로 부터 정압과정으로 팽창하는 경우 dP = 0 이 되므로 열량변화는 엔탈피의 변화와 같게 된다.
2. 정상유동에 대한 일반 에너지식
[정상유동] 어느 관로의 한점에 대한 흐름의 상태가 시간에 관계없이 일정한 것을 정상유동이라고 한다. 이 유동과정 중의 에너지 변화식을 구하기 위하여 아래 그림과 같은 관로의 두 단면을 생각해 보자.
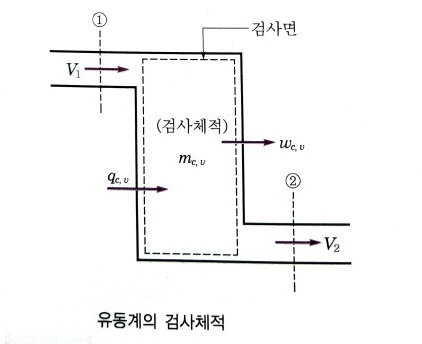
단면 ①에서의 압력 P1 [N/㎡], 비체적 V1 [㎥/㎏], 내부에너지 u1 [J/㎏], 속도 v1 [m/s],
위치에너지 z1 [m]라 하고 그림의 단면 ② 에서의 압력 P2 [N/㎡], 비체적 V2 [㎥/㎏], 내부에너지 u2 [J/㎏], 속도 v2 [m/s], 위치에너지 z2 [m] 라 할 때 단면 1에 유입되는 단위 질량당 에너지 e1 은 다음과 같이 나타낼 수 있다.
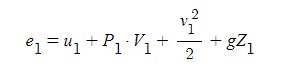
또한 단면 2에서의 비에너지 e2는 다음과 같이 표현할 수 있다.
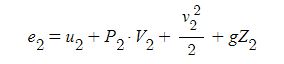
여기서,

이 때, 단면 1과 2 사이에서 외부로 부터 계의 qc, v [J/㎏]의 열을 가하였고, 또 계가 외부에 wc, v [J/㎏] 의 일을 했다고 한다면 열역학 제1법칙에 의하여 한 계에 흘러 들어 온 에너지와 흘러 나간 에너지는 같게 되므로 다음과 같은 식이 성립한다.
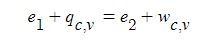
위 식을 앞의 식에 대입하면 다음과 같은 식을 얻을 수 있다.
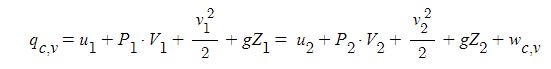
이 되며, 이를 비엔탈피식에 대입하면 다음과 같은 정상유동계의 에너지방정식을 얻을 수 있다.
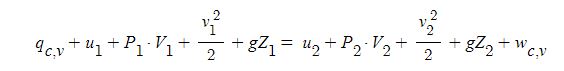
만약 위치가가 크지 않을 때라면 z1, z2는 양변에서 무시할 수 있다. 또한 위치에너지 뿐만 아니라 입구와 출구의 속도차가 크지 않을 경우, 즉, 유속이 30 ~ 50 [m/sec] 이하일 때는 양변에서 운동에너지를 무시해도 큰 문제가 없을 때는 위식은
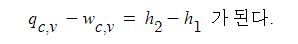
여기서, 단열유동인 경우는 qcv = 0 으로 가정하게 되므로 1, 2 구간에서 발생한 일의 크기는 결국
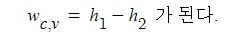
#엔탈피 #enthalpy #에너지식 #정압과정 #단열과정 #열역학 #에너지보존법칙
#질량 #비에너지식 #내부에너지 #운동에너지 #위치에너지
'소방설비기사 (기계) > 소방유체역학' 카테고리의 다른 글
| 열역학과 에너지 (4) | 2023.12.18 |
|---|---|
| 일과 열의 비교 관련 문제 풀이 (0) | 2023.09.15 |
| 부력 (浮力) 이란 ? (0) | 2023.09.06 |
| 펌프의 이상현상 (0) | 2023.09.06 |
| 배관의 주손실과 부차적 손실 (0) | 2023.09.05 |
