아낌없이 주는 나무

1. 기본량의 단위계와 차원

2. 중력단위와 절대단위의 차원비교

3. 압력 환산인자

4. 점도의 단위​​

5. 점도의 종류

6. 비압축성 유체와 압축성 유체

 가. 비압축성 유체

   ① 액체는 보통 비압축성 유체

   ② 물체 (굴뚝, 건물 등) 둘레를 흐르는 기류

   ③ 달리는 물체 (자동차, 기차 등) 주위의 기류

   ④ 저속으로 나는 항공기 둘레의 기류

   ⑤ 물속을 주행하는 잠수함 둘레의 기류

​

 나. 압축성 유체

   ① 기체는 보통 압축성 유체

   ② 음속 보다 빠른 비행체 주위의 공기 흐름

   ③ 수압철관 속의 수격 작용

   ④ 디젤엔진에 있어서 연료 수송관의 충격파

​

7. 단위와 차원

 가. 힘의 단위​

 나. 일의 단위​

 다. 동력의 단위​

9. 1차원 정상류의 연속방정식

  ▣ 질량 보존의 원리를 적용하여 연속방정식을 구할 수 있다.

  ▣ 평균속도, 밀도, 단면적을 각각, V1, V2, ρ1, ρ2, A1, A2 라 하면 단위시간에 단위면적을 통과하는 유체

       질량은 같으므로​

  ▣ 여기서 m 을 질량 유량 (mass flowrate)이라 하고, 이 식의 미분형은 다음과 같다.

          d (ρ ·A·V) = 0 ------ 식2

    그러므로, 연속방정식은​

   비압축성 유체이면 ρ = 일정이므로 위의 식은 다음과 같이 변형할 수 있다.​

10. 중량 유량과 체적 유량

  ▣ 압축성 유체의 정상흐름에서는 유관의 모든 단면을 통과하는 질량 유량 (또는 중량 유량)이 일정하고,

       비압축성 유체의 정상흐름에서는 유관의 모든 단면을 통과하는 체적 유량이 일정하다.​

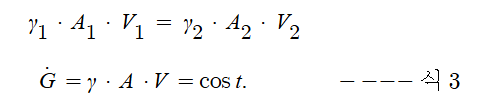
     여기서, G = 중량유량 (weight flowrate)

     만약, 비압축성 유체라면

11. 오일러 운동방정식

  ▣ 유선 또는 미소단면적의 유관을 따라 움직이는 비점성 유체의 요소에 뉴턴의 운동 제2법칙을 적용하여

       얻은 미분방정식을 오일러 (Euler)의 운동방정식이라 한다.

 ▣ 오일러의 운동방정식은 다음과 같이 나타낼 수 있다.​

12. 베르누이 방정식

  ▣ 베르누이 방정식은 유체역학적인 에너지 보존법칙이며, 일반적인 흐름에 적용가능하고 비점성 유체에

       적용가능한 오일러의 운동방정식에 몇 개의 가정조건을 대입함으로써 얻을 수 있다.

  ▣ 실제 관로에서 유체의 마찰을 고려한 수정 베르누이 방정식은 다음과 같다.​

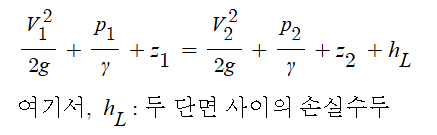
#차원 #단위 #질량 #속도 #중력가속도 #비중량 #뉴턴 #점도 #유체 #압축성 #베르누이 #오일러 #연속방정식

물체의 운동 상태를 변화시키려고 하는 외력에 저항하는 성질의 힘을 관성력(inertia force)이라 한다. 액체 상태인 물은 외력과 관성력에 평형하도록 운동한다. 물의 거동을 해석하기 위해서는 외력인 중력, 압력, 물의 밀도, 압축성, 점성 등의 물리적 성질에 관한 이해가 필요하다.

어떤 물질의 단위체적에 대한 질량의 비를 밀도(density)라 하며, 지구 중심에서 물체를 잡아 당기는 가속도를 중력가속도로 한다. 단위중량(unit weigth)은 단위 체적당의 중량으로 밀도와 중력가속도를 곱한 값이다. 질량과 단위중량과의 관계를 좀 더 살펴보기 위하여 먼저 중력가속도에 대해 좀 더 알아 보자. 뉴턴이 발견한 만유인력은 행성의 반경을 R, 질량을 M (행성의 질량), m (물체의 질량), 중력상수를 G(gravitational constant)라 하면 어떤 물체에 작용하는 중력은 GmM/R2 으로 나타낼 수 있다. 행성이 지구처럼 크다면( 반경 약 6,370km) 행성의 표면에서 어느 정도 떨어진 곳이라 할지라도 지구 반지름에 비해 아주 미소한 크기이므로 중력은 행성 표면과 거의 비슷하다고 할 수 있다.

지구에서 질량 m인 물체에 작용하는 중력(W)은 중력가속도를 g(9.8m/s2)라 하면 뉴턴의 제2법칙에 의하여 다음과 같이 표현된다.

W = mg 식 (1.1)

따라서 지구에서 중력에 의한 중력가속도는 다음과 같이 나타낼 수 있다.

식 (1.1)에서 알 수 있듯이 중력가속도는 물체의 질량과 관계가 없다. 행성(지구)의 질량과 관계가 있다. 식 (1.1)와 식 (1.2)에서 나타낸 바와 같이 물체의 무게는 만유인력, 즉 중력으로 중력가속도가 지구 중심에서 얼마나 떨어져 있는냐 (장소)에 따라 다르기 때문에 같은 물체라도 무게는 장소에 따라 다르다. 지구는 일반적으로 적도의 반경이 크고 극지방의 반경이 작으므로 같은 물체의 중량은 적도 지역에서 보다는 극지방에서 약간 클 것이다.

물체의 체적을 V, 중량을 W, 중력 가속도를 g, 질량을 m 이라고 하면 밀도 와 단위 중량 는 다음과 같이 나타낼 수 있다.​

여기서, 중량의 차원은 [W] ≒ [F] ≒ [MLT−2] , 중력가속도의 차원은 [g] ≒ [LT−2], 부피

의 차원은 [Vo] ≒ [L3] 이다. 따라서 밀도와 단위중량의 차원은 MLT와 FLT에서 각각 다음과 같이 표현된다.​

따라서 MLT와 FLT 차원에서 밀도의 단위는 각각 kg/m3과 kg/m2 ⋅ s2이고,

단위중량의 단위는 각각 kgf ⋅ s2/m4과 kgf/m3이다.

물의 밀도는 근소하지만 동일 기압이라 할지라도 수온에 따라서, 동일 온도라 하더라도 압력에 따라서 변화한다.

​

#밀도 #비중량 #가속도 #중력가속도 #만유인력 #뉴턴 #차원 #질량 #중량

​

​물체의 운동 상태를 변화시키려고 하는 외력에 저항하는 성질의 힘을 관성력(inertia force)이라 한다. 액체 상태인 물은 외력과 관성력에 평형하도록 운동한다. 물의 거동을 해석하기 위해서는 외력인 중력, 압력, 물의 밀도, 압축성, 점성 등의 물리적 성질에 관한 이해가 필요하다.

어떤 물질의 단위체적에 대한 질량의 비를 밀도(density)라 하며, 지구 중심에서 물체를 잡아당기는 가속도를 중력가속도로 한다. 단위중량(unit weigth)은 단위체적당의 중량으로 밀도와 중력가속도를 곱한 값이다. 질량과 단위중량과의 관계를 좀 더 살펴보기 위하여 먼저 중력가속도에 대해 좀 더 알아보자. 뉴턴이 발견한 만유인력은 행성의 반경을 R, 질량을 M (행성의 질량), m (물체의 질량), 중력상수를 G(gravitational constant)라 하면 어떤 물체에 작용하는 중력은 GmM/R2 으로 나타낼 수 있다. 행성이 지구처럼 크다면( 반경 약 6,370km) 행성의 표면에서 어느 정도 떨어진 곳이라 할지라도 지구 반지름에 비해 아주 미소한 크기이므로 중력은 행성 표면과 거의 비슷하다고 할 수 있다.

지구에서 질량 m인 물체에 작용하는 중력(W)은 중력가속도를 g(9.8m/s2)라 하면 뉴턴의 제2법칙에 의하여 다음과 같이 표현된다.

     W = mg 식 (1.1)

따라서 지구에서 중력에 의한 중력가속도는 다음과 같이 나타낼 수 있다.​

식 (1.1)에서 알 수 있듯이 중력가속도는 물체의 질량과 관계가 없다. 행성(지구)의 질량과 관계가 있다. 식 (1.1)와 식 (1.2)에서 나타낸 바와 같이 물체의 무게는 만유인력, 즉 중력으로 중력가속도가 지구 중심에서 얼마나 떨어져 있는냐 (장소)에 따라 다르기 때문에 같은 물체라도 무게는 장소에 따라 다르다. 지구는 일반적으로 적도의 반경이 크고 극지방의 반경이 작으므로 같은 물체의 중량은 적도 지역에서 보다는 극지방에서 약간 클 것이다.

물체의 체적을 V, 중량을 W, 중력 가속도를 g, 질량을 m 이라고 하면 밀도 와 단위 중량은 다음과 같이 나타낼 수 있다.​

여기서, 중량의 차원은 [W] ≒ [F] ≒ [MLT−2] , 중력가속도의 차원은 [g] ≒ [LT−2], 부피

의 차원은 [Vo] ≒ [L3] 이다. 따라서 밀도와 단위중량의 차원은 MLT와 FLT에서 각각 다음과 같이 표현된다.​

따라서 MLT와 FLT 차원에서 밀도의 단위는 각각 kg/m3과 kg/m2 ⋅ s2이고,

단위중량의 단위는 각각 kgf ⋅ s2/m4과 kgf/m3이다.

물의 밀도는 근소하지만 동일 기압이라 할지라도 수온에 따라서, 동일 온도라 하더라도 압력에 따라서 변화한다.

​

#밀도 #비중량 #가속도 #중력가속도 #만유인력 #뉴턴 #차원 #질량 #중량

【 단위 】

우리나라는 미터계를 쓰고 있으나 영연방국가 들은 영국 단위계를 쓰는 곳도 있다.

 ▣ 미터계 (Metric unit system) : 우리나라

 ▣ 영국단위 계 (Britesh unit system)

  ⊙ 1 [m] = 3.2808 [ft]

  ⊙ g (중력가속도) = 9.8 [m/sec2) = 32.2 [ft/sec2]

​

【 힘 (무게) 】

▣ 마찰이나 저항이 없는 어떤 물체에 추가적인 속도를 내게 하는 원천으로 일반적으로 힘 = 질량 × 가속도 라고 표현한다.

   F = ma                            F : 힘

      = ㎏·㎝/sec2                m : 질량 [㎏]

      = ㎏ ·m/sec2                a : 가속도 (cf : g : 중력가속도)

      = N

    ∴ 1[N] = 1 [ ㎏ ·m/sec2 ] cf) 중량 [㎏f] : 1kg × g = 9.8 kg ·m/sec2

​

【 밀도, 비중량 (단위중량), 비중 】

  ▣ 밀도는 단위 체적당 질량을 말한다.

       여기서 단위라는 말은 "1" 을 의미하므로 일반적으로 미터단위계에서는 1[㎥] 당 질량을 말한다.

       이를 식으로 나타내면 다음과 같다. ​

  ▣ 비중 : 4 [℃] 물의 체적과 동일한 체적의 무게비를 말한다.​

   ⊙ 단위중량 (비중량) : 단위 체적당 무게 (무게 = 질량 × 중력가속도)

​

 ▣ 단위 중량 (비중량) : 단위 체적당 중량(무게)​

     cf : 물의 밀도 : 1,000 [㎏/㎥]

           물의 비중량 : 9,800 [N/㎥]

​

 ▣ 차원

  ⊙ 물리적인 관계를 나타내는 물리량은 기본량을 적당히 조합해서 지수의 꼴로 나타낼 수 있다. 이 때 물리량을 나타내는

       단위를 차원이라고 한다.

       일반적으로 물리량은 질량[M], 길이 [L], 시간[T]을 기본량으로 한 [MLT]계를 이용하여 표현할 수 있다.

  ex)  F = m·a = 질량 × 가속도 = 질량 × (거리/시간) / 시간

        [F] = [M] · [LT -2] = [MLT -2]​

  ex : 밀도를 [MLT] 차원으로 나타내면 ?

  단위에 대한 접두사​

 ex : 비중병의 무게가 비었을 때는 무게가 2N이고, 액체로 충만되어 있을 때는 8 [N] 이었다. 액체의 체적이 0.5 [ℓ] 이면

        이 액체의 비중량은 몇 [N/㎥] 인가 ?​

 ex) 압력과 에너지, 운동량의 차원은 ?

   cf : 압력 (P) = F/A, 에너지(일) = 힘 × 거리= F · L, 운동량 = 힘 × 시간 = F · T

    풀이 : 압력 = [MLT-2] / [L2] = [ML-1T-2]

              에너지 = [MLT-2] × [L] = [ML2T-2]

              운동량 = [MLT-2] × [T] = [MLT-1]

​

ex : 표면장력의 차원은 ?​

▣ 물의 점성

 ⊙ 물분자가 상대적인 운동을 할 때 물분자간 혹은 물분자와 고체 경계면 사이에 마찰력을 유발하는 물의 성질, 마찰력은

      전단응력이라고 하는데 이 전단응력으로 인하여 물체의 상판을 움직이면 유체가 따라 움직임의 정도가 깊이에 따라

      달라지게 된다. 따라서 전단응력의 변화율을 깊이의 변화율로 나눈 것이 전단응력이 되는데 이때의 비례상수를

      점성계수라고 한다.

   평판의 면적 : A

   평판의 단위 면적당 마찰력 : τ (전단응력)​

▣ 동점성 계수​

ex : 점성계수와 동점성계수의 차원은 ?

 ▣ 점성계수는 전단응력과 전단속도와 깊이와 비율과의 관계나타내 주는 상수를 말한다.​

▣ 동점성계수는 점성계수를 밀도로 나눈 값이다.​

#질량 #밀도 #차원 #점성계수 #동점성계수 #비중량 #비중 #전단력 #전단응력 #점성

#표면장력 #가속도

1. 시스템, 상태, 속성

​

유체의 성질 그 2번째로 시스템, 상태, 속성에 대하여 알아 보자. 시스템은 분석대상 즉, 물

질자체나 공간을 의미하고 주변은 시스템이 아닌 어떤 물질이나 공간을 말하고 경계는 시스

템과 주변을 구분하는 면을 말한다.

​

위 그림은 대표적인 수리시설 실험모형이다. 수로에 따라 물이 방수되는 형태를 보여준다.

붉은 색 선으로 구분되는 영역이 있는데 이 영역은 수로상의 물 뿐만 아니라 수로에서 방출

된 물까지 포함하고 있다. 만약 수리시설에서 방출되는 시설을 분석대상으로 삼는다면

바로 이 물이 시스템, 즉 분석대상이 되고 물을 제외한 나머지 영역들 즉, 공기, 시설물, 사

람 등이 주변이라고 할 수 있다. 그리고 붉은 색 선과 같이 시스템과 주변을 구분하는 면이

경계가 되겠다.

​

위 그림은 스킨스쿠버가 산소통을 메고 물속에 있는 그림이다. 만약에 우리가 산소통에서

사람에게 공급되는 공기를 유체역학적 관점에서 분석한다면 분석대상이 되는 시스템은

탱크속에 있는 공기와 호수를 통해 공급되는 공기가 되겠고 이 공기가 시스템이 되며

공기외의 다른 모두가 주변이라고 할 수 있다. 경계는 산소탱크와 호수가 주변과 접하는

면이라고 할 수 있다.

그런데 여기에서 새로운 개념이 나타난다. 속성(Property)라는 것인데 속성이란 현재

시스템이 나타내는 정량적인 상태를 말한다. 예를 들면 산소탱크 내의 공기의 밀도, 압력,

등이 속성이 된다. 프로세스는 상태의 변화과정이다. 스킨스쿠버가 호흡을 하면 산소탱크

내에 있는 공기의 양이 줄어 들게 된다. 산소의 양이란 속성이 시간이 변함에 따라 변화하게

되는데 이를 프로세스라고 한다. 그런데 산소탱크의 무게 등은 시간의 변화에 무관하게

일정한 상태를 유지하게 되는 이를 정상상태라고 부른다.

▣ 운동학적 속성

▣ 물질의 속성

​

또 하나의 예를 들면, 위 그림을 보면 밀폐된 실린더에 피스톤이 꼽혀 있다. 그 안에는 공기

가 들어 있다. 만약에 피스톤에 충분히 강한 힘을 가해서 피스톤을 아래로 누르면 공기가

압축되어 위그림의 오른쪽 그림과 같이 될 것이다. 실린더 안에 들어 있는 공기를 시스템

이라고 하고 공기의 형태를 나타내는 정량적인 것들을 속성이라고 한다면 대표적인 속성은

압력, 온도, 부피 등이 된다. 이와같이 가해진 힘에 의해 시스템의 속성이 변했을 때 우리는 프로세스가 진행되었다고 한다.

실린더 안의 압력, 온도, 부피를 속성이라고 했는데 이러한 속성을 구분하는 대표적인 것이

운동학적 속성과 물질의 속성이다. 피스톤에 힘을 가하면 공기입자에 힘이 가해져서 공기

입자가 이동을 하게 되는데 이와 같이 질량을 갖는 물질이 이동을 하는 현상, 질량을 갖는

물질의 위치, 속도, 가속도를 운동학이라고 했다. 위와 같이 운동학적 관점에서 보이는

시스템의 상태, 속성을 운동학적 속성이라고 한다. 반면 피스톤에 힘을 가하기 전의 공기의

위치, 질량, 압력 등은 물질의 속성이라고 한다.

​

물질의 속성을 어떻게 나타낼 수 있을까 ?

​

​

속성(Property)는 물질의 속성을 나타내는 정량적인 양 또는 시스템의 상태를 말한다.

물질의 속성에는 질량에 관련된 속성 즉, 밀도, 비중량(단위중량), 비중이 있고 점성과 관련

된 속성에는 점성과 동점성이 있고 기타 속성에는 표면장력, 증기압, 탄성계수 등이 있다.

​

2. 단위(Unit)와 차원 (Dimension)​

차원과 단위를 어떻게 구분할까 ?

흔히 길이 [m], 질량 [kg]을 차원과 혼용하여 쓰는 경우가 있다. 위 그림은 힘을 나타내는

그림인데, 힘, 즉 Newton을 수평축의 눈금으로 나타낸다면 한 눈금을 100 [Newton]이

라고 하면 이런 눈금을 힘(속성)의 단위라고 할 수 있다.

우리가 3차원 세계에 살고 있다고 하는데 3차원을 구성하는 지표상의 위도와 경도 그리고

수직방향을 나타내는 고도로 구성된 것이 3차원인데 이 때 위도, 경도, 고도가 차원이고

위도와 경도를 나타내는 [°]와 고도를 나타내는 [m]가 단위가 된다.

​

▣ 무차원수 (Dimensionless number)

차원의 해석의 관점에 관한 것인데 차원의 해석하면 떠오르는 것이 무차원수와 차원의

동차이다. 차원은 단위가 있다. 그런데 물질의 상태를 정의하는데 차원은 차원인데 무차원

인 속성이 있다. 단위가 없는 차원을 정의할 때 무차원수가 등장을 한다.

위 그림은 유체역학에서 가장 많이 쓰이는 네이놀즈의 수라는 것인다. 레이놀즈의 수는

Re로 표현한다. 레이놀즈수는 V : 물질의 속도, D : 두께, 길이, 깊이 ρ : 유체의 질량,

μ : 흘러가는 매질의 점성 을 나타낸다. 그런데 단위를 보면 분자, 분모의 단위가 모두

상쇄되어 단위가 없게 된다. 이와같은 수를 무차원수라고 한다.

​

▣ 차원의 동차 (Dimensional homogeneity)

​

​

위 그림은 기체의 압력과 질량과 부피를 다루는 이상기체 방정식을 보여주고 있다.

P : 압려, ρ : 밀도, T : 온도, R : 기체상수를 나타낸다.

압력은 힘을 면적으로 나눈 것이다. 밀도는 질양을 부피 [㎥]로 나눈다, 온도는 캘빈온도로

나타낸다. 압력은 질량나누기 길이 곱하기 온도의 제곱이 되고 우변도 똑같은 단위로 나타

낼 수 있다. 즉, 좌변과 우변이 차원이 같게 되는데 이와같은 경우를 차원의 동차라고 한다.

어떤 방정식을 볼 때 좌변과 우변을 정리한 다음 양변의 차원이 다르게 되면 그 방정식은

잘못된 방정식이라고 생각하면 된다.

​

#차원 #동차 #온도 #부피 #질량 #방정식 #압력 #유체 #시스템 #상태 #속성 #단위

#경계 #위치 #속도 #가속도 #운동학 #질량 #3차원 #눈금 #무차원수

【 일의 중력 단위 변환】

▣ 일의 단위 N · m는 국제표준단위이지만 절대단위로서 이는 지구상에서는 존재하지 않는 단위이다. 따라서 지구상에

     존재하는 실제의 일 단위인 중력단위로 변환해 보자.

▣ 절대단위를 중력단위로 변환할 때는 절대단위를 중력단위 변환계수 gc로 나눠준다.

  ⊙ 중력단위 변환계수 gc= 9.8 ㎏ · m / ㎏f · sec2 이다.​

【 동력 (Power) 】

▣ 동력은 일률이라고도 한다. 즉, 시간분의 일의 양으로 시간당 얼마만큼 일을 할 수 있는지를 나타낸다. 일반인에게는

     동력을 힘으로 오해를 하는데 동력은 힘을 넘어선 개념으로 일을 할 수 있는 능력 즉 에너지를 말한다.

※ 일률을 이해하려면 만약에 어떤 사람이 2㎏의 박스 2개를 1층에서 5층으로 옮겼다고 하면 일의 물리량은 알 수 있지만

     소요된 시간은 알 수 없으므로 일을 잘하는 것인지 못하는 것인지는 알 수가 없다. 따라서 일률 (일하는 능력)을 알아

     보려면 시간의 개념을 넣어서 10분에 했다든지 하여 비교를 하게 되면 일의 능력을 알 수가 있다.

     이렇게 일할 수 있는 능력을 동력(일률)이라고 한다.

⊙ 동력 = 일량 / 시간 = Joule / sec

             = ㎏ · ㎡ / sec3 [Watt]

  ex : 1[Watt]의 동력을 중력단위로 바꾸어 보자.

      중력단위 = 절대단위 / gc​

【 압력 (Pressure) 】

▣ 압력은 특정한 면에 작용하는 힘을 말한다.

  ⊙ 압력 = 수직력 / 면적 = N / ㎡ [Pa]​

  ※ 수직력 : 힘 또는 전압력이라고도 한다.

​

【 온도 (Temperature) 】

▣ 국제표준온도 : 절대온도 [K] Kelvin 온도

  ① 섭씨온도 : 물이 어는 점 0 [℃] 와 물이 끓는점 100 [℃] 사이를 100 등분한 온도단위

  ② 화씨온도 : 물이 어느점 32 [˚F] 와 물이 끓는점 212 [˚F]를 180 등분한 온도단위

  ◈ 섭씨온도와 화씨 온도간에 변환을 하여 보자​

【 밀도 (Density)】

▣ 밀도는 단위 부피당 질량을 말한다. 즉, 밀도는 질량을 부피로 나누어 산정한다. 그런데 질량은 변화하지 않으므로 밀도

     는 동일 무게에 차지하는 부피의 크기에 따라 달라지게 된다.​

① 기체의 밀도

 가. 표준상태 (0 ℃, 1기압)인 경우​

  ※ 모든 기체는 아보가드로의 법칙에 의하여 0 [℃], 1기압에서 1 [mol]의 부피가 22.4 ℓ 이다.

  ※ 1[mol]의 질량은 그 물질의 분자량과 같다.

​

 나. 표준상태가 아닌 경우

【비중량 (Specific Weight)】

▣ 위에서 밀도는 단위 부피당 질량이라고 말하였다. 그런데 질량이란 절대단위는 지구상에는 존재하지 않으므로 밀도도

     가상적인 의미의 단위이다. 따라서 지구상에서 실제 존재하는 밀도의 개념이 필요한데 비중량이란 개념으로 이끌어

     낸다. 비중량은 밀도와 같이 같이 단위 부피당 중량을 의미한다. 그러므로 비중량은 중량을 부피로 나누어 산정하게

     되는데 중량은 질량 × 중력가속도이므로 비중량은 밀도 × 중력가속도가 된다.​

  ※ 질량 × 중력가속도 = 중량

      밀도 × 중력가속도 = 비중량

  ※ 질량에 중력가속도를 곱하면 중량이 된다. 질량은 중력가속도를 받지 않는다. 밀도는 중력가속도를 받지 않는 질량을

      부피로 나누어 산정한다. 이 밀도에 지구상에 있는 모든 물질은 중력가속도를 받게 되므로 중력가속도를 곱하면 비중

      량이 된다. 거꾸로 말하면 밀도라는 것은 비중량의 개념이 들어가 있다. 즉, 밀도는 여러 물질과 비교한 무게라는

      개념이다. 단위 부피당 무게라는 것은 물질간 무게를 비교한 개념인 것이다.

​

 ② 중력단위

   예를 들어 물의 밀도를 비중량으로 바꾸어 보자.

   물은 1㎏ / ℓ ⇒ 1,000 ㎏ / ㎥ 이다.

            1,000 ㎏ / ㎥ × 9.8 m / s2 = 9,800 N / s2

이번에는 질량으로 나타낸 몸무게를 중량으로 나타내 보자.

[중력단위 변환 연습]​

[ 비중 (Specific Gravity) ] : 무차원수

▣ 비중은 어떤 특정 물질을 기준으로 하여 그 물질이 대비되는 밀도나 비중량을 말한다.

    이는 무차원수로서 단위가 없어 차원이 없다.​​

  ① 액체, 고체의 비중​

  ② 기체의 비중​

  ※ 프로판가스의 밀도를 구해 보자​

【 비체적】

 ▣ 밀도의 역수를 말한다.

 ▣ 비체적은 어떤 물질의 단위 무게, 즉 질량에 대한 차지하는 부피의 비율을 말한다.

      이것도 기준물질에 대비하는 개념이다.​

#힘 #물리량 #유체역학 #일 #중력가속도 #비체적 #밀도 #비중 #차원 #물질 #온도 #섭씨 #화씨 #중력 #동력 #비중량 #질량 #중량 #속도 #거리 #부피 #비율 #압력 #전단력 #전단응력