아낌없이 주는 나무

정수력을 적용하기 위해서는 작용점을 알아야 한다.

작용점을 알기 위해서는 정수압이 최종적으로 작용하는 면의 특성을 알아야 한다.

정수력이 작용하는 면이 곡면, 평면, 기타 면이냐에 따라 정수력의 작용이 달라지게 된다.

위 그림은 2차적인 면에 따라 기하학적 도형의 특징을 보여준다.

삼각형을 보면 밑변의 길이가 "b"이고 높이가 'h'이다. 이 삼각형의 도심은 밑변에서 높이

방향으로 1/3 지점에 있다는 것을 알 수 있다. 각각의 도형의 특징은 면적, 도심 등이 있다.

​

Centroid (도심), Center of Gravity (무게 중심)

​

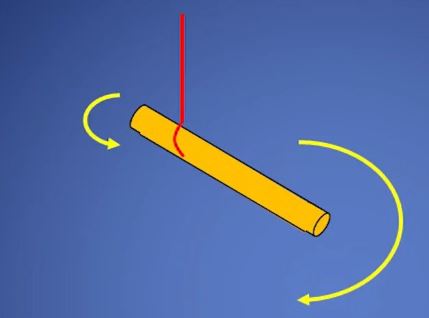
위 그림과 같이 같은 굵기의 무게가 일정한 봉을 그림과 같이 한쪽에 치워쳐 끈으로 묶어

들게 되면 끈을 중심으로 긴쪽으로 기울고 또한 시계방향으로 회전하게 된다.

이는 긴 쪽에 무게가 더 나가고 큰 모멘트가 작용하기 때문이다.

​

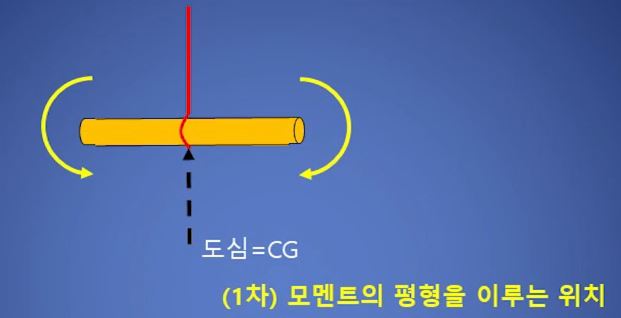
반매 막대의 정중앙에 끈을 매달아 들게 되면 막대는 평형을 이루게 될 것이다.

이는 끈을 중심으로 좌우의 무게가 같고 모멘트도 상호 정반대방향으로 크기가 같기 때문에 서로 상쇄되기 때문이다. 이 때 끈으로 묶은 지점을 도심 또는 무게 중심이라고 한다.

​

위 그림은 특정한 형상을 갖는 물체의 도심을 찾는 과정을 나타낸다. 위와같은 형상을 갖는

물체의 도심을 찾아 끈으로 매단다고 한다면 위 그림의 물체는 평형을 이루게 될 것이다.

도심을 찾아 매달았을 때 균형을 이루려면 위 물체는 모든 면에서 밀도가 균일하여야 한다.

또한 매달기 위해서 위 형태의 미소면적의 하중의 합과 같은 힘으로 매달아야 한다.

​

도심과 무게중심의 차이에 대해 알아 보자

​

위 그림은 막대에 밀도가 다른 무거운 물질을 붙인 후 도심부분에 끈으로 묶어서 들었다.

그러면 위 그림에서 보는 바와 같이 끈을 중심으로 좌우의 무게가 동일하지 않으므로

무거운 쪽으로 막대는 기울고 또한 시계방향으로 움직이게 될 것이다.

이와 같이 위 그림에서는 가운데 점이 도심이기는 하지만 무게 중심은 아니게 된다.

도심과 무게중심은 같을 수도 있고 다를 수도 있다. 도심과 무게 중심이 같으려면

그 물체를 구성하는 물질이 균질하여야 한다. 즉 단위면적당, 단위길이당 질량이 일정해야

한다.

​

​

물체를 구성하는 물질이 균질하지 않은 경우 무게 중심은 무거운 쪽으로 이동시키면 된다.

무게 중심에서는 좌우 힘의 평형을 이루게 된다. 또한 무게 중심에서는 모멘트가 같아지게

되므로 물체는 균형을 이루게 된다.

정리하면 도심은 면적, 길이와 같은 1차 모멘트의 중심을 말한다.

반면 무게 중심은 질량을 중심으로 한 1차 모멘트의 중심을 말한다.

여기서 1차 모멘트는 (힘, 거리) 곱하기 중심으로 부터의 거리를 말한다.

​

위 그림을 보면서 일반적인 형태의 도형의 도심과 무게 중심을 찾는 과정을 알아 보자.

수식상으로 무게 중심을 구하는 식은 선을 기준으로 무게 중심을 구하기 때문에 체적의 무

게 중심을 구하기 위해서는 체적을 면적으로 면적을 선으로 변환하는 과정이 필요하다.

따라서 체적을 미분하면 면으로 면을 미분하면 선이 되는데 x축을 기준으로 하는 모멘트와

x축을 기준으로 하는 모멘트로 구분하기 때문에 시작을 면을 기준으로 하므로 한번 미분을

하여 선을 기준으로 하는 모멘트를 구하고 이를 적분하여 전체의 모멘트를 구하게 된다.

위 그림의 오른쪽 그림을 보면 직사각형의 판이 놓여져 있다. 직사각형 판의 두께를 t라고

하고 길이 수평방향을 x축, 높이 방향을 y축이라고 하자. 이 직사각형 단면 모양에 도심의

위치를 yc 라고 하자. 물론 x축 방향의 도심의 위치도 같은 방법으로 찾을 수 있다. 왼쪽

그림은 이 직사각형 판을 x,y축의 관점에서 본 것이다. 즉, 위에서 바라 본 모양이다.

따라서 위 쪽 방향은 z축이 된다. x축의 길이는 "b"이고 y축 방향으로 yc만큼의 거리에

도심이 있다고 하자. 그러면 도심을 식으로 정의할 수 있다. 위와 같이 균일한 물질로 되어

있는 경우에는 도심과 무게 중심이 같게 된다. 무게 중심은 x축을 중심으로 이 판에 작용하

는 모든 힘들을, 힘에 의한 모멘트의 중심이라고 하였다. 무게 중심은 x축을 중심으로 이 판

에 작용하는 모든 힘들을, 힘에 의한 모멘트를 상쇄할 수 있는 어떤 힘이 작용하되, 그 힘이

작용하는 위치가 바로 도심의 위치 yc라고 할 수 있다. Y방향의 단위면적을 생각해 보자.

x축 방향으로는 폭이 일정하니까 y축 방향의 작은 폭을 갖는 조각을 dy라고 하자. 그럼,

이 dy라고 하는 조각에 중력에 의하여 가해지는 힘, 만약 아래쪽(지면)으로 가해진다고

하면 작은 조각에 작용하는 힘을 dF라고 하면 dF = γ tbdy라고 할 수 있다. 중력은 비중력

× 체적이기 때문이다. 여기서, γ는 단위중량(비중량), t는 무게, b는 x축 길이이고, dy는 미

소 y축 길이가 된다. 따라서 γtbdy가 이 미소조각에 작용하는 중력의 힘이라고 할 수 있다.

이 미소면적에 작용하는 힘을 모두 더하면 이 판에 작용하는 힘 F가 될 것이다. 그런데

"0"점을 기준으로 미소요소까지의 거리는 y축에 따라 변하게 된다. y축에 따라 dF라는 힘

에 의해서 작용하는 모멘트의 총합이 그 판재의 전체 무게인 F를 판재 위에 어딘가에 작용

해서 반대방향의 모멘트를 작용하면서 평형을 이룰 수 있다면 그것이 바로 단면 1차 모멘

트 중심 즉 도심이 될 것이다. 즉, 전체 힘은 γtbh가 될 것이고 이 힘에 여기에다가 우리가

구할려고 하는 모멘트의 중심 yc를 곱하면 모멘트가 될 것이다. 모멘트는 힘 × 거리(중심에

서 거리)라고 하였다. 이것이 무엇과 같을 까 ? 각 미소요소에 작용하는 힘 dF에 거기까지

의 거리 y를 곱한 모멘트 즉, ydF를 y방향으로 적분해 준 것과 같아지게 되고 이 것이 결국

힘 모멘트의 평형 중심이 된다. 위 식을 적분을 하면 yc = h/2이 된다.

​

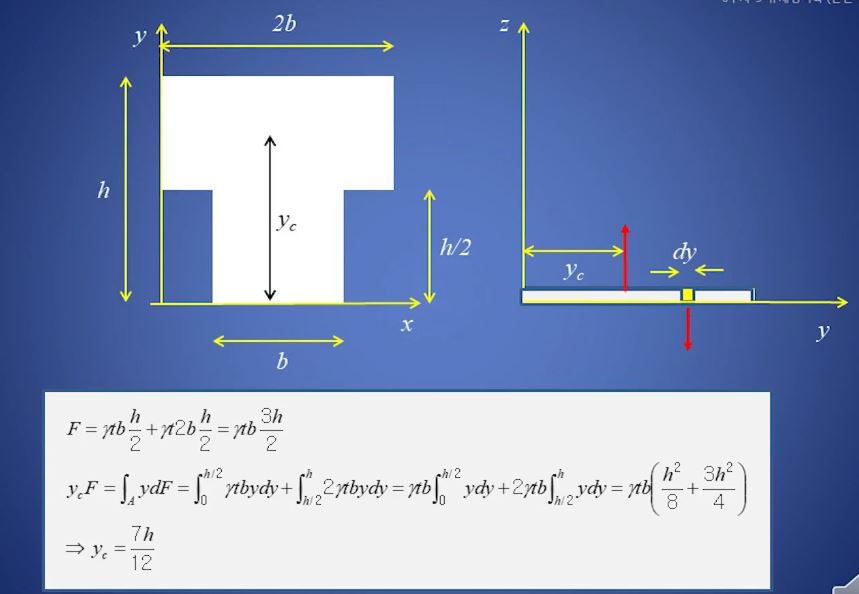
앞서 폭이 일정할 때에는 무게 중심을 구하는 것이 단순하였는데 위 그림과 같이 폭이 변화

하는 경우는 좀 복잡해진다. 이 때 무게 중심을 찾는 방법에 대하여 알아 보자.

이 경우 x축을 기준으로 하는 이 평면의 무게 중심을 알아 보자. 먼저 전체 면적에 받는 힘은

단위중량 × 체적이므로 F = γ tb(h/2)+ γ t2b(h/2) = γ tb(3/2h)가 된다.

이 때 x축 방향의 모멘트를 구하면 무게 중심점에 모든 중량이 걸린다고 할 수 있으므로

ycF를 통하여 구할 수 있고 위 그림의 아래식과 같다. 그런데 모양이 정형이 아닌 여러가지

모양으로 변할 때 무게 중심을 간단히 구하는 방법은 다음과 같다.

위 단면적 전체에 작용하는 힘은 γtb3/2h라는 것을 이미 알았다. 이 힘을 이용하여 각각의

분할된 면적에 작용하는 전체힘과 분할된 면적의 yc에 작용하는 모멘트를 같게 하면 그 분

할된 면적의 무게중심이 된다. 따라서 무게 중심점을 찾기 쉽게 하기 위해서는 부정형 모양

을 중심점을 찾기 쉬운 정형의 모양으로 분할하면 중심점을 찾기 쉬워진다.

이번에는 모멘트 이누시아 또는 단면 이차 모멘트에 대해 알아 보자. 앞에서 살펴 본 바와

같이 폭이 "b"이고 높이가 "h"인 직사각형이 있다고 하자. 그리고 우리가 yc라는 무게 중심

을 알고 있다고 하자. 직사각형 이니까 무게 중심이 지나는 선을 h/2의 선이 될 것이다.

이번에는 도심을 지나는 선인 h/2 선을 x축이라고 하고 직사각형의 밑변을 지나는 선을

x'라고 하자. 단면 2차 모멘트 즉 도심을 지나는 축을 기준으로 하는 2차 모멘트 Ixx는 미소

면적 dA에다가 그 축으로 부터의 거리 y의 제곱를 곱한 것을 적분한 것으로 정의한다.

또한 도심을 지나는 축이 아닌 임의의 축 즉, 위 그림에서 직사각형의 밑변을 지나는 축을

기준으로 하는 2차 모멘트는 도심을 지나는 2차 모멘트와 면적 A와 도심까지의 거리의

제곱을 곱한 것을 합한 값으로 나타낸다.

​

#모멘트 #무게중심 #질량중심 #도심 #정수력 #단위중량 #비중량 #기하학 #직사각형

#미분 #적분

1. 질량중심

▣ 질량중심 (質量中心) 은 물체 전체의 질량의 중심점으로 전체 질량이 질량 중심에 있는 것처럼 외부 계와 작용한다.

    미분질량의 위치를 질량가중치(미분질량/전체질량)를 곱하여 적분한 것이다. 중력이 균일한 경우 무게 중심과 같기

    때문에 혼용하기도 한다.  이 때 물체의 각 부분에 작용하는 중력를 합한 합력의 작용점을 무게 중심이라고 한다.

​

2. 직선에 놓인 점들의 질량 중심

아래 그림과 같이 지렛대가 놓은 받침점을 원점으로 하여 좌표 xk인 점에 질량 mk가 놓여 다고 가정하자. (k = 1,2,3)

각 질량 mk에 아래 쪽으로 중력이 작용한다. 중력가속도 g가 작용하여 원점을 중심으로 회전하려는 힘이 생긴다.

이 힘을 토크(toque)로 부르는데 크기는 gmk이고 부호는 위치 xk에 따라 결정된다. 양(+)이면 시계방향으로 음(-)이면

반시계 방향으로 회전하는 힘이 작용한다. 토크를 모두 더한 값이 시스템 토크다.  (참고 토크 τ는 변위 벡터 r과 힘 F의

외적이다. τ = r × F 이다. 따라서 편하기 다루기 위해  '+'는 반시 계방향, '-'는 시계방향인 오른손 법칙을 따라 방향을 정한다)

시스템 토크가 0이면 어느 쪽으로도 기울지 않는다. 시스템은 균형을 이룬다. 시스템 토크를 다시 정리하면 아래와 같다.​

여기서 중력가속도 g는 시스템의 환경에 따라 달라진다. 지구라면 중력가속도 9.8 [m/sec2) 이지만 다른 천체라도면 달라

질 것이다. 하지만 중력가속도를 제외한 m1x1+ m2x2 + m3x3는 환경에 영향이 없이 어디서든 똑같다. 이 값을 원점에

대한 모멘트 (moment of the system about the origin)이라고 하며 식으로는 다음과 같다.​

시스템이 균형을 이루는 점을 찾아 보자. 균형점 x바에 대한 토크는 질양 mk가 있는 위치 (xk-x')와 중력가속도의 곱이 토크

의 합이 0이 되어야 균형점이다.

이 식을 x바에 대한 식으로 정리하면 다음과 같다.​

위 식에서는 질량이 질량중심에 집중되어 있다면 그것의 모멘트는 전체 모멘트의 합과 같음을 의미한다. 이는 질량이

균일할 경우인데 만약 질량이 균일하지 않으면 밀도가 함수로 주어질 것이고 함수를 적용하여 계산하게 된다.

밀도 = 질량 / 길이(체적)을 말한다. 따라서 질량은 밀도 × 길이가 된다. 즉, △mk = δ(x) × △xk가 된다. 따라서 질량중심을

밀도로 나타낸 다면 다음과 같이 나타낼 수 있다.​

3. 평면에 놓인 질량중심

​

평면 위에 작용하는 질량 중심을 알아 보기 위해서는 먼저 면적을 선의 개념으로 변환하는 것이 필요하다. 면적을 선개념

으로 변환하기 위해서는 미분을 해야 하는데 여기서는 미분방법 보다는 x축, y축을 기준으로 하여 모멘트를 구하는 방식을

취한다. x축을 기준으로 한다는 말 속에는 x축을 미분하여 한 점으로 만든다는 의미와 같게 된다. 그 이유는 x축을 기준으

로 하는 모멘트 예를 들어 my1x1, my1x2, my1x3, my1x4 ··· my1xn은 모두 x축을 기준으로 하는 모멘트 같기 때문이다.

따라서 x축을 기준으로 한다고 하면 어떤 주어진 면을 y축으로 평행한 선으로 변형할 수 있게 된다. y축을 기준으로 할 때

에도 x축을 기준으로 할 때와 같다. 이를 바탕으로 면에 대한 질량 중심을 구할 수 있게 된다.

이제 면적에 대한 질량중심을 알아 보도록 하자.

평면위에 좌표 (xk,yk)인 점에 질량 mk가 놓여 있다고 하자. 즉, 이 평면은 질량이 일정한 균질의 평면이라고 하자.

이 때 이 평면의 전체 질량 M은 각각의 질량의 합이 될 것이고 x축과 y축에 대한 모멘트는 다음과 같은 식으로 표현할 수

있다.

또한 질량중심을 좌표 x바, y바라고 한다면 이는 다음 식으로 나타낼 수 있다.​

질량이 두께가 아주 얇고 평평한 판에 고르게 퍼져 있다고 가정하면 위에서 정리한 내용을 폭이 "0"에 아주 가까운 매우

가는 띠로 나누어 구하는 것으로 생각할 수 있다. 이는 x축을 미분하는 것으로 앞에서 말한 바와 같이 x축을 기준으로 하면

모멘트는 y축 방향으로 x으로 부터 떨어진 거리에 의해 영향을 받고 x축 방향으로 y축에서 떨어진 값 즉, x값에는 영향을

받지 않기 때문이다. 따라서 x축은 선전체를 한 점으로 생각해도 된다. 이제 y축에 평행한 직선으로 n등분하고 부분합을

구하고 이 부분합의 극한값을 구하는 것은 바로 정정적분으로 질량중심을 구하는 것이 된다.

위 식에서 띠의 넓이를 A라고 하고 미분면적의 질량 dm 대신에 밀도 δ가 주어진다면 질량 dm 대신에 δdA를 대입하면

된다.

​

예제 : 세 직선 y = 2x, y = 0, x = 1로 둘러 쌓인 삼각형에 밀도 δ = 3g /㎠ 로 고르게 질량이 분포되어 있다고 할 때 질량중심

          을 구하여라.

위 그림과 같이 먼저 y축과 평행하고 폭이 dx인 띠를 생각하자. 이 때의 질량중심으로 (x출결, y물결)이라고 하면 띠의 면적 A는 미분면적으로 2xds가 되고 미분면적에 대한 질량은

미분밀도와 면적의 곱이 된다. 이를 이용하여 식을 전개하면 다음과 같다.​

질량중심 y 좌표도 x좌표와 동일한 방식으로 구할 수 있다.

#무게중심 #질량중심 #밀도 #질량 #적분 #미분 #모멘트 #평면 #직선

미분의 개념을 이야기할 때 미분계수는 어떤 함수의 특정점에서 접선의 기울기값이라고 했다.

특정 점에서 접선의 기울기를 구하기 위하여 극한값을 구하는 과정도 알아 보았다.

그런데 함수 y = f(x)에 대하여 f'(1), f'(2), f'(3) … f'(100)을 구한다면 미분계수의 정의

를 이용하여 미분값을 구한다면 평균변화율의 극한값을 100번을 계산하여야 하는데 이는

번거롭고 효율적이지 못하다. 이런 경우에 x에서의 f'(x)를 함수값으로 하는 새로운 함수

y = f'(x)를 구하여 x값을 대입하면 보다 효율적으로 미분값을 계산할 수 있다.

이와 같이 어떤 함수 y = f(x) 함수에서 x값에 있어서의 미분값으로 하는 새로운 함수

y = f' (x)를 y = f(x)의 도함수라고 한다.

​

1. 도함수의 뜻

​

가. 도함수의 정의

함수 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는​

따라서 f(x) = x2 의 x = a 에서의 미분계수 f'(a) 는 a의 값을 2배하여 구할 수 있다. 즉,

f'(1) = 2, f'(√2) =2 √2, f'(π) = 2π, … f'(x) = 2x 이다.

일반적으로 함수 y = f(x)가 정의역 X에서 미분가능하면 정의역에 속하는 모든 x에 대하여

미분계수 f'(x)를 대응시키는 새로운 함수​

이를 그림으로 나타내면 다음과 같다.

이 때, 함수 f'(x)를 f(x)의 도함수라고 하고, 이것을 기호로

함수 y = f(x) 에서 그 도함수 f'(x)를 구하는 것을 함수 y = f(x)를 x에 대하여 미분한다고 하고 그 계산법을 미분법이라고

한다.​

【평균변화율, 미분계수, 도함수의 비교】

함수 y = f(x) 에서​

   ① 구간에서 x의 증분과 y의 증분의 비율

   ② 기하학적 의미 : 두 점 P(a, f(a), Q (b, f(b))를 지나는 직선의 기울기​

   ① 특정한 값 x = a 에서 평균변화율의 극한

   ② 기하학적 의미 : 곡선 y = f(x) 위의 점 P(a, f(a) 에서의 접선의 기울기​

   ① 특정값이 아닌 정의역에 속하는 임의의 x에 대한 미분계수 함수

   ② 기하학적 의미 : 곡선 y = f(x) 위의 임의의 점 (x, f(x))에서의 접선의 기울기

​

2. 미분법의 공식

도함수의 정의에서 도함수가 존재한다면 주어진 함수의 도함수를 구할 수 있게 된다.

그런데 도함수를 구할 때 정의에 의한 극한의 식으로 도함수를 구하기는 번거롭게 복잡

하다. 따라서 도함수를 구할 때 정의에 의해서 구하는 것보다 공식으로 도함수를 구하면

쉽고 편리하게 구할 수 있다.

​

가. 도함수의 정의에 이용하여 함수 f(x) = xn (n은 양의 정수)의 도함수를 구해 보자.​

인수분해 하면​

나. 상수함수 f(x) = C (C는 상수)의 도함수는

상수함수는 모든 점에서의 접선의 기울기가 항상 0이라는 것을 알 수 있다.

한편 아래의 미분법의 공식과 함수 y = xn 의 미분법을 이용하면 도함수의 정의를 이용하지

않더라도 다항함수​

의 도함수를 구할 수 있다.

【미분법의 도함수】

 두 함수 f(x), g(x)의 도함수가 존재할 때

   ① y = cf(x) 이면 y' = c f'(x) (단, c 는 상수)

   ② y = f(x) ± g(x) 이면 y' = f'(x) ± g'(x) (복부호 동순)

   ③ y = f(x) g(x) 이면 y' = f'(x) g(x) + f(x) g'(x) 가 된다.

또한 세함수 f(x), g(x), h(x)가 미분가능하면 함수 y = f(x) g(x) h(x) 도 미분가능하고

y' =f'(x) g(x) h(x)+ f(x) g'(x) h(x)+ f(x) g(x) h'(x) 이다.

​

다. 구간별로 정의된 함수의 도함수

구간별로 정의된 함수

f(x)= x (x < 0), x3 (x≥0) 의 도함수를 구할 때

각 구간의 도함수를 구하여 다음과 같이 나타내는 잘못을 해서는 안된다.

f'(x) = 1 (x <0), 3x2 (x ≥0)

구간의 경계가 되는 x = 0에서 평균변화율의 우극한은 0, 좌극한은 1로 같지 않기 때문에

x = 0 에서의 미분계수는 존재하지 않게 된다.

따라서 아래와 같이 나타내야 한다.

f'(x) = 1 (x <0), 3x2 (x >0)

일반적으로 구간별로 정의된 함수가 주어졌을 때, 그 구간의 경계점에서의 미분가능성은 알

수 없다. 경계점에서 미분가능하려면 미분계수가 존재해야 한다. 즉, 경계점에서의 평균변

화율의 극한이 존재해야 하므로 반드시 우극한과 좌극한이 서로 같은지 확인해야 한다.

참고로​

x = a 를 기준으로 나눠서 정의된 다항함수에서의 기하학적인 의미의 y = f(x)의 그래프가

x = a 에서 이어져 있고, 우극한에서의 접선의 기울기와 좌극한에서의 접선의 기울기가

같아야 한다.

​

#도함수 #비분 #우극한 #좌극한 #기하학 #다항함수 #기울기 #미분계수 #함수 #경계점

#평균변화율 #극한 #접선 #정의역 #방정식 #상수 #상수함수

또한 x의 증분에 대한 y의 증분의 비율​

위 식을 x값이 a에서 b로 변할 때의 함수 y=f(x)의 평균변화율이라고 한다.

함수 y=f(x)의 평균변화율은 두점 P(a, f(a)), Q (b,f(b))을 지나는 직선의 기울기와 같다.​

나. 미분계수 (순간변화율)

함수 y=f(x)에서 x의 값이 a 에서 a+△x (=b)까지 변할 때, 평균변화율은 다음과 같다.​

여기서 △x → 0 일 때 평균변화율의 극한값이​

함수 y=f(x)는 x=a에서 미분가능하다고 하고 이 극한값을 함수 y=f(x)의 x=a에서의 순간변화율 또는 미분계수라고 하며

기호로는 f'(a)와 같이 나타내고 f prime a라고 한다. 또한 함수가 어떤 구간에 속하는 모든 x의 값에서 미분가능할 때,

함수 y=f(x)는 그 구간에 서 미분가능하다고 한다. 특히 함수 y=f(x)가 정의역에 속하는 모든 x 의 값에서 미분가능할 때

함수 y=f(x)는 미분가능한 함수라고 한다. 한편, a+△x=x라고 하면 △x=x-a이고 △x →0일 때 x→a 이므로​

다음 함수는 미분이 가능할까 ?​

함수 f(x)=x2 은 x=2에서 미분가능하고 그 때의 미분계수는 f'(2)= 4 이다.

​

[정리하면]

함수 y = f(x)에 대하여

① x의 값이 a에서 b까지 변할 때의 평균변화율은​

② x = a 에서의 미분계수(순간변화율)은​

또한 미분계수(순간변화율)은 다음과 같이 나타낼 수도 있다.​

다. 미분계수의 기하학적 의미

앞에서 x의 값이 a 에서 b까지 변할 때 함수 y=f(x)의 평균변화율​

따라서 함수 y=f(x)의 x = a 에서의 미분계수

곡선 y=f(x) 위의 점 P(a,f(a))에서의 접선 ℓ의 기울기와 같음을 알 수 있다.

[미분계수 f'(a)의 기하학적 의미

함수 y=f(x)에 대하여 x=a에서의 미분계수 f'(a)는 곡선 y=f(x) 위의 점 (a, f(a)에서의 접선의 기울기와 같다.

점 (a, f(a))에서의 접선이 x축의 양방향과 이루는 각을 θ 라 하면, 미분계수 f'(a)는 다음과 같다. f'(a) = tan θ

​

[평균변화율과 미분계수의 대소 관계]

평균변화율과 미분계수의 기하학적 의미를 이용하면 그 대소 관계를 알 수 있다.

함수 y=f(x)의 그래프가 위 그림과 같을 때, 다음 식의 값의 대소를 비교하여 보자.

다음 함수 y=f(x)의 그래프가 다음 그림과 같을 때

다음 식의 값의 크기를 비교해 보자.​

위 그래프는 아래로 볼록한 그래프로 위 식의 크기는 다음과 같다.​

2. 미분가능과 연속

앞에서 미분계수의 기하학적 의미는 곡선의 접선의 기울기와 같다고 했다. 그런데 불연속점

에서는 접선을 그릴 수 없으므로 미분이 가능하지 않다는 것을 예상할 수 있다.

그러면 연속인 점에서는 항상 접선을 그릴 수 있어 미분도 가능할까 ? 이에 대한 생각을 하

면서 y = f(x)의 연속과 미분가능 사이에는 어떤 관계가 있는지 알아 보자.

​

가. 미분가능 : 연속

함수 y = f(x)가 x = a에서 미분가능하면 함수 y=f(x)는 x=a에서 연속이다.

[증명]

함수 f(x)가 x = a 에서 미분가능하면 미분계수​

f'(a)는 일정한 값이므로 다음이 성립한다.​

따라서​

나. 연속 ≠ 미분가능

앞의 명제의 역 '함수 y = f(x)가 x = a 에서 연속이면 y = f(x)는 x = a 에서 미분가능하다'

는 거짓이다. 즉, 함수 y = f(x)가 x = a 에서 연속이지만 y = f(x)는 x = a 에서 미분가능하지 않을 수 있다.

[증명]

함수 f(x) = ㅣx l 를 예로 들어 봅시다.

함수 f(x)는 x = 0 에서 미분가능하지 않다. 따라서 함수 f(x) = ㅣxㅣ는 x = 0 에서 연속이지만 미분가능하지는 않습니다.

미분 계수는 함수의 극한으로 정의되어 있다. 함수의 극한에서 좌극한과 우극한이 같은 값에 수렴할 때 함수의 극한이

존재한다고 한다. 즉, 미분계수가 존재하려면 △x → 0 일 때 평균변화율의 좌극한과 우극한이 같아야 한다.

따라서 위와 같은 반례에 의해 함수의 연속성이 함수의 미분가능성을 보장하지는 않는다.

즉, 함수 y = f(x)는 x = a 에서 연속이어도 일반적은로 함수 y = f(x)가 x = a 에서 미분이 가능한 것은 아니다. 또한 위의

함수에서와 같이 x = a 에서 연속이지만 x = a 에서 뽀족하면 (부드럽지 않으면) x = a 에서 미분가능하지 않다.

이러한 점을 뾰족한 점 또는 첨점이라 고 한다.

[함수의 미분가능과 연속]

함수 y = f(x)가 x = a 에서 미분가능하면 함수 y = f(x)는 x = a 에서 연속이다.

그러나 그 역은 일반적으로 성립하지 않는다.

[위 명제의 대우]

'함수 y = f(x)가 x = a 에서 연속이 아니면 함수 y = f(x) 는 x = a 에서 미분가능하지 않다' 도 성립한다.

[이차함수 접선의 기울기]

1. 미분

​

독립변수 x가 연속적으로 변함에 따라 종속변수 y도 연속적으로 변할 때 어느 한 점에서 종속변수 변화량 Δx와 독립변수 변화량 Δy의 비율의 극한을 그 점에서의 ‘미분계수’ 또는 ‘순간변화율’이라고 합니다.

이에 비해 단순히 종속변수 변화량 Δx 와 독립변수 변화량 Δy의 비율을 평균변화율이라 하죠.

​

1-1. 평균변화율

​

x가 a로부터 a+Δx인 b로 변화될 때 함수 f(x)의 평균 변화율은 다음과 같습니다.

​

아래 [그림 1]에서 파랑색 직선의 기울기가 평균변화율을 뜻합니다.

1-2. 순간변화율 (미분계수)

(1)식에서 Δx→0일 때의 극한값이 순간변화율입니다. 수학적으로 표현하면 아래 식과 같습니다.​​

[그림 1]에서 주황색 직선의 기울기가 a인 지점에서의 순간변화율을 뜻합니다.

​

[예제1] 순간변화율​

[풀이] 아래와 같이 미분계수는 1/2이 나옵니다. 한편 풀이에서 빨강색 부분은 같은 양을 나누고 곱해주었음을 뜻합니다.​

[예제2] 도함수

[풀이] 도함수는 아래와 같이 구해집니다.​

한편, x=1에서의 미분계수를 구한고자 한다면 위의 도함수에서 x대신에 1을 대입하면 됩니다.

그러면 (E-1)식과 같이 1/2이 동일하게 구해지는 것을 알 수 있습니다.

결국 도함수를 구해 놓으면 어느 지점에서건 미분계수를 쉽게 구할 수 있게 됩니다.

​

1-4. 상미분

​

위에서 도함수를 구하는 과정을 미분이라고 했는데요. 이때 원래 함수의 독립변수가 하나인 경우 이 함수를 미분하는 것을 상미분이라고 합니다.

통상적인 미분이라는 뜻이에요.

상미분 개념은 예를 들어 어떤 기계장치의 온도가 기계로 들어가는 교류신호의 실효값에만 의존하는 경우 실효전압의 크기가 증가함에 따라 온도가 어떠한 기울기로 증가하는 지를 알고자 할 때 적용할 수 있습니다.

구체적인 예로는 위 [예제2]가 바로 상미분에 해당합니다. 예제에서 x를 교류 실효값의 크기라 생각하고 f(x)를 온도라고 생각하면 됩니다.

​

1-5. 편미분

​

상미분은 변수가 하나인 경우의 미분이라면 편미분은 변수가 2개 이상인 경우의 미분법을 말합니다.

편미분은 하나의 변수에 대해 미분할 때 다른 변수는 상수로 취급합니다.

편미분 개념은 어떤 기계 장치의 온도가 기계로 들어가는 교류 실효값뿐만 아니라 압력에도 의존한다고 생각해봐요. 그러면 실효값과 압력이 달라지면 온도가 달라지는거에요.

이때 압력을 고정하고, 즉 압력을 상수로 취급하고 실효값에 따른 온도의 기울기를 구하는 방법이 편미분입니다. 물론 실효값을 상수로서 고정하고 압력에 따른 온도의 기울기를 구하는 것도 편미분입니다.

편미분의 기호는 다음과 같습니다. 예를 들어 변수가 여러개인 함수 f를 x로 편미분하고자 한다면 아래와 같이 쓰면 됩니다.​

[예제3] 편미분​

이 함수를 x와 y에 관해 각각 편미분하여라.

​

[풀이]

먼저 x에 관해 편미분부터 하면, y를 상수로 취급하면 됩니다.

이때 상수를 미분하면 0이 되는 것을 상기하세요.​

다음에는 y에 관해 편미분하면 x를 상수로 취급하면 됩니다.

2. 미분방정식 (Differential equation)

​미분방정식이란 ‘하나 또는 그 이상의 독립변수에 관하여 하나 또는 그 이상의 종속변수의 도함수 또는 미분을 포함하는 방정식’을 말합니다.

특히 독립변수가 하나인 경우 상미분방정식(상미방, ODE, Ordinary Differential Equation), 두개 이

상인 경우 편미분방정식(편미방, PDE, Partial Differential Equation)이라고 부릅니다.

​

2-1. 상미분방정식

​

상미분방정식의 예시는 다음과 같습니다.​

(6)식을 보시면 y를 x로 미분하는 dy/dx항이 수식에 포함된 것을 볼 수 있어요.

이렇게 주어진 미분방정식을 푼다는 말은 독립변수가 x이고 종속변수가 y인 함수 y=f(x)를 구한다

는 의미로 보시면 됩니다.

​

2-2. 편미분방정식

​

편미분방정식의 예시는 다음과 같습니다.

(7)식을 보시면 u를 t로 편미분, u를 x로 편미분, u를 y로 편미분하는 내용이 포함된 방정식임을 알 수 있어요. 이렇게 주어진 편미분방정식을 푼다는 말은 독립변수가 x, y, t이고 종속변수가 u인

함수 u=f(x,y,t)를 구한다는 의미로 보시면 됩니다.

​

3. 미분방정식 구분

​

미분방정식은 다양한 모양을 가질 수가 있어요. 미분을 2번하는 방정식, 3번하는 방정식도 있을 수 있고 상미분과 편미분으로 구성된 방정식도 있을 수 있어요.

그래서 미분방정식을 구분하기 위한 이름이 있어야 합니다. 이때 사용되는 것이 미분방정식의 ‘계수’와 ‘차수’, ‘선형’과 ‘비선형’입니다.

​

3-1. 계수와 차수, 선형과 비선형

​

계수란 미분방정식에 포함되는 최고계 도함수의 계수를 말합니다.

미분이 한번인 dy/dx는 1계, d2y/dx2 는 2계가 됩니다. 미분방정식에서 주어지는 도함수의 가장

큰 계수를 기준으로 이름이 붙습니다.

또한 차수란 미분방정식에 포함되어 있는 최고계 도함수의 지수를 말합니다.

예를 들어 (y′′′)3 은 지수가 3이므로 3차가 됩니다.

선형 미분방정식은 종속변수와 그 도함수가 1차이고 각 계수가 독립변수에만 의존하는 것을 말합니다.

이에 비해 비선형 미분방정식은 종속변수와 그 도함수가 지수를 갖거나 계수가 종속변수를 포함하거나, 비선형 함수 등을 포함하는 경우를 말합니다.

​

3-2. 미분방정식 구분의 예​

(10)식에서 3계 도함수가 3제곱이므로 3차 미분방정식이 되며, 또한 이 때문에 도함수가 1차가 아니므로 비선형이 됩니다. 차수는 최고계 도함수를 기준으로 결정된다는 것을 기억하세요.​

(12)식에서 종속변수인 u가 제곱(즉, 2차)의 형태여서 1차가 아니므로 비선형 방정식이 됩니다.​

(13)식은 계수 (1−y)가 종속변수를 포함하여 독립변수만으로 구성되어 있지 않으므로 비선형이 됩니다.​

(14)식은 종속변수가 비선형함수로서 1차가 아니므로 비선형이 됩니다.

​

#미분 #방정식 #미분방정식 #편미분 #비선형함수 #선형함수 #독립변수 #종속변수 #계수 #차수

#도함수 #함수 #실효값 #상수 #변화율 #순간변화율 #접선 #기울기

​

1. 미분방정식이란 ?

​

미분방정식이 왜 중요한 걸까 ?

우리가 사는 세상의 모든 물체를 볼 때 물체의 변화(운동, 상태 등)에 관심을 갖기 때문이다.

물체의 변화는 움직임일 수도 있고 얼었다 녹는 상태의 변화일 수도 있고 부피나 모양의

변화일 수 있다. 이처럼 우리는 물체의 변화에 관심을 갖게 되는데 이런 물체의 변화를 나타내는 것이 미분이다.

물체의 변화 중에서 속도를 예를 들어 보자. 물체의 속도에는 3가지가 있다.

▣ 속도가 없거나

▣ 속도가 일정하거나

▣ 속가 변하거나 이 3가지가 있다.

​

그런데 속도는 거리(L)를 시간(t)로 미분한 것(dℓ/dt)인 것이다.

속도를 수식으로 표현하면 미분항 (dℓ/dt)이 들어가는 미분방정식으로 표현하게 된다.

뉴턴의 운동법칙 1,2,3법칙 중에서 제1법칙이 관성의 법칙이다.

관성의 법칙도 등속도를 유지하려는 법칙이므로 속도와 관련되어 미분과 관련이 있다.

뉴턴의 제1법칙은 속도의 특수한 경우인 "0"인 경우를 제외하고 등속도에 관한 법칙이다.

뉴턴의 제1법칙을 식으로 나타내면 속도 v = k(일정)이 되며​

뉴턴의 제2법칙은 가속도에 관한 법칙이다. 이것도 미분방정식에 해당한다.

뉴턴의 가속도의 법칙도 식으로 나타내면 다음과 같다.​

이처럼 가속도도 미분방정식과 관련이 있다.

​

상대성원리도 마찬가지이다. 상대성원리는 물체가 빛의 속도에 가깝게 빠르게 움직일 때

두드러지게 나타나는 현상인데 그중 특수상대성 원리란 등속도에 관한 것이고 일반상대성

원리는 가속도 운동에 관한 것이다. 이 상대성 원리도 속도와 관련된 사항이므로 미분

방정식에 해당하는 것이다.

우리가 관심을 갖고 있는 것들을 식으로 나타내면 이처럼 많은 것들이 미분방정식으로

표현되는 것들이다. 왜냐하면 우리는 변화하는 것들에 대하여 관심이 많기 때문이다.

​

2. 간단한 미분방정식의 예

【 뉴톤 역학 】

① 썰매장에서 몸무게 50[kg]의 아이를 5[Newton]의 힘으로 계속하여 밀면 10초 후에는 아이는 얼마의 속도로 밀려

     나갈까 ? (얼음과의 마찰력은 없다고 가정한다)

 [풀이] 뉴턴의 제2법칙 가속도의 법칙에 의하면 가속도는 다음과 같다.​

여기서 F = 5N, 질량(아이 몸무게) = 50kg 이므로 이를 위식에 대입하면​

v(10) 을 구하기 위해서는 C를 구해야 하는데 C는 초기조건이라고 한다. 조건에서

처음상태는 아이를 밀기 전이므로 즉, 처음에 아이는 정지해 있었으므로 v(0) = 0이다.

위 식에서 시간 t = 0 일 때 속도 v = 0, v(0) = 0 을 만족해야 한다.​

② 위 조건에서 10초 후에는 처음 위치에서 얼마만큼 떨어져 있겠는가 ?

  ▣ 잘못된 풀이 : ℓ = v × t 이므로 ℓ = 1 × 10 = 10 [m] 이다.

  ▣ 올바른 풀이법 : 아이를 밀 때 계속하여 힘을 가해 주므로 가속도 운동을 하게 된다.

처음 밀 때 속도가 "0" 에서 변화를 하므로 위에서 처럼 등속도 운동으로 풀면 안된다.

속도 v(t)는 거리를 시간으로 미분한 것이다.​

거리(ℓ)을 풀기 위해서 양변을 적분을 하면 다음과 같다.​

여기서도 초기조건 C은 정지상태이므로 ℓ(0) = 0 이란 조건을 이용하여 C를 구한다. 

#미분 #적분 #미분방정식 #뉴턴 #관성법칙 #가속도 #운동법칙 #변화율 #접선 #속도